- Daikin Industries, Ltd., Technology and Innovation Center, Osaka, Japan
Functionally Gradient (Graded) Materials (FGMs) represent a class of advanced materials characterized by spatial distributions in composition and structure, resulting in corresponding changes in their material properties. The material properties depend on the micro-structures, which are also heavily influenced by fabrication processes. This paper provides an overview of the modeling and design of micro-structures in FGMs, highlighting historical developments, current technologies such as multi-scale modeling using the Finite Element Method, the evolution of modeling techniques, and the latest research trends, including the application of deep learning and AI. The advanced fabrication of FGMs by additive manufacturing will be covered in view of the resultant micro-structures. Furthermore, energy conversion FGMs will be investigated concerning the transport properties in grain boundaries and lattice structures.
1 Introduction
Functionally Gradient (Graded) Materials (FGMs) represent a class of advanced materials characterized by spatial distributions in composition and structure, which result in corresponding changes in their properties. These materials are designed to meet specific performance requirements that traditional homogeneous materials cannot achieve. FGMs were initially developed in Japan (Niino et al., 1987; Niino et al., 1988a; Niino et al., 1988b; Hirano et al., 1990; Hirano et al., 1991; Sasaki et al., 1989; Sata, 1993) to address the need for materials that can withstand extreme thermal gradients, such as those in aerospace and nuclear applications. The significance of FGMs lies in their ability to combine the best properties of different materials within a single component. For example, an FGM can have a high temperature-resistant surface on one side and a structural material on the other side, and between the two surfaces, graded compositional layers for the thermal stress-mitigation core. This gradation in properties is achieved through the optimum design of the phase gradation considering those material’s micro-structures, which is the focus of this paper.
Micro-structures play a crucial role in determining the overall behavior of FGMs (Hirano et al., 1990; Hirano et al., 1991; Eshelby, 1957). By manipulating the micro-structural features, such as grain shape and size, phase distribution, and porosity, etc., we can tailor the material properties to meet specific needs. However, even with the same phase composition, the formed micro-structures depend on the fabrication processes. Therefore, the modeling and design of these micro-structures and phase distribution are essential for optimizing the performance of FGMs (Sasaki et al., 1989; Sata, 1993; Fukui, 1991; Kawai et al., 1992).
Traditional materials research has primarily focused on an analytical approach, wherein the physical properties and micro-structures of materials synthesized through various processes are analyzed and evaluated. However, the primary goal of FGMs development lies in the practical utilization of their unique properties. From this perspective, a synthetic approach, namely, how to design and fabricate materials that exhibit the desired properties, becomes a critical issue (Niino et al., 1987; Hirano et al., 1990; Hirano et al., 1991; Sasaki et al., 1989; Sata, 1993). While the conventional analytical approach represents a forward problem, in which the properties of a given material are evaluated, the design of FGMs can be defined as an inverse problem (Hirano et al., 1990; Hirano et al., 1991), where the required properties are specified first, and the corresponding micro-structures and synthesis methods are determined accordingly. Therefore, in order to enable the design of FGMs, it is essential not only to accurately estimate material properties, but also to control structural parameters such as micro-structures so that the properties can be tailored to meet specific requirements during fabrication (Niino et al., 1987; Hirano et al., 1990; Hirano et al., 1991).
This paper aims to provide a comprehensive overview of the historical developments, current technologies, and future prospects related to the optimal design of compositional gradients and the modeling of micro-structures in FGMs. It covers the evolution of modeling techniques, the integration of advanced computational methods, and the latest research trends, including the application of deep learning and AI as well as new material design and manufacturing methodologies.
Additionally, this review covers Energy Conversion FGMs (Hirano et al., 1994; Hirano, 1995), especially on the thermoelectric materials improvement, in view of lattice and micro-structures improving the Energy Conversion efficiency (Hicks and Dresselhaus, 1993; Whitlow and Hirano, 1995; Nishio and Hirano, 1997). This field of research is quite rapidly advancing in view of carrier energy filtering of electron and phonon transport phenomena.
2 Historical background
2.1 Early research and development of FGMs and micro-structure modeling
The concept of FGMs was first introduced in Japan in 1984 during a space plane project (Niino et al., 1987; Niino et al., 1988a; Niino et al., 1988b; Hirano et al., 1990). The goal was to develop materials that could serve as thermal barriers capable of withstanding extreme temperature gradients. Specifically, the materials needed to endure surface temperatures of up to 2000 K and a temperature gradient of 1000 K across a 10 mm section. This initial application highlighted the potential of FGMs in aerospace and other high-temperature environments. Early research on FGMs focused on the inverse optimum design of the phase composition utilizing classical or empirical micro-structure models and the development of processing techniques to create the desired gradation in the phase composition. Figure 1a depicts the concept of FGMs with ceramics, metal and micro-pore (Hirano et al., 1991), Figure 1b depicts the phase distributions of two different materials (VA and VB) with micro-pore (VP) expressed by power function VA(x) = 1 – VB(x)n–VP(x), Figure 1c shows Eshelby’s Ellipsoidal Inclusion model (Eshelby, 1957). Table 1 shows several Rules of Mixtures based on Micro-structures (Hirano et al., 1990).
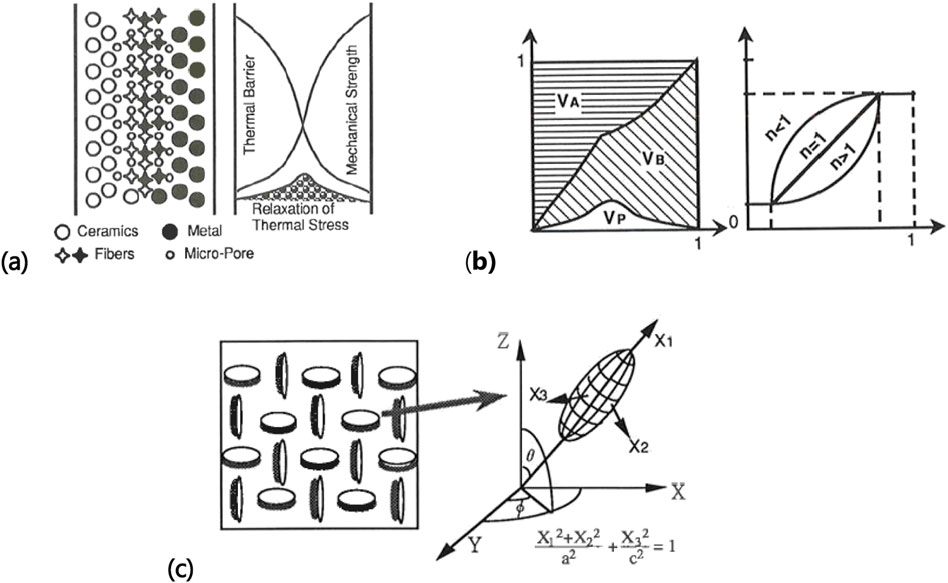
Figure 1. (a) Concept of FGMs. (b) Phase compositions of different materials (Hirano et al., 1990, 1991) (c) Eshelby’s Ellipsoidal Inclusion model (Eshelby, 1957).
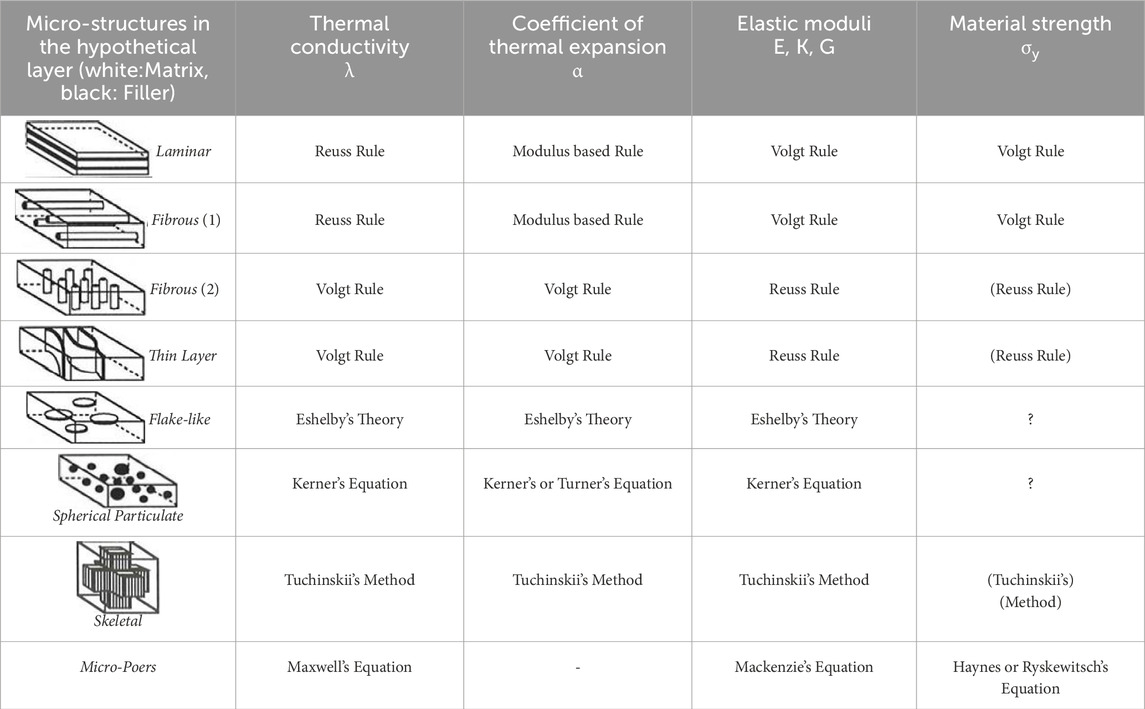
Table 1. Rules of Mixtures based upon Micro-structures (Hirano et al., 1990).
Researchers explored various methods including chemical vapor deposition (Niino et al., 1988a; Sasaki et al., 1989), powder metallurgy (Niino et al., 1988b; Sata, 1993) and centrifugal casting (Fukui, 1991) to fabricate FGMs with tailored properties. As the field progressed, the scope of FGMs applications expanded beyond aerospace to include biomedical, automotive, and energy sectors. For example, FGMs have been used in dental implants (Kondo et al., 2004) and bone prostheses due to their ability to mimic the natural gradation of properties found in biological tissues (Bohuder et al., 2014).
2.2 Evolution of evaluation methods with elasto-plasticity
As mentioned above, the micro-structure modeling and optimum design of the phase composition in FGMs played a crucial role in the development of FGMs. Early models were primarily based on linear analyses, focusing on simple gradation profiles and basic material properties. However, with advancements in computational power and numerical methods, more sophisticated models emerged. In recent years, the integration of advanced computational techniques, such as Finite Element Method (FEM) (Kawai et al., 1992; Teraki et al., 1992; Arai et al., 1993) and multi-scale modeling, has further enhanced the ability to design and optimize FGMs. These methods enable researchers to predict the behavior of FGMs to tailor their properties under various loading conditions including fabrication and specific applications. The historical development of FGMs reflects a continuous effort to improve material performance through innovative design and modeling techniques. The advancements in micro-structure modeling have been instrumental in realizing the full potential of FGMs across a wide range of applications.
2.3 Energy conversion FGMs (EC-FGMs)
Subsequently in Japan, fundamental research on Functionally Gradient (Graded) Energy Conversion Materials (EC-FGMs) was advanced as a national project to dramatically improve the conversion efficiency of energy conversion materials (Hirano et al., 1994). Thermoelectric (TE) conversion materials and photovoltaic conversion materials, among other energy conversion materials, are inorganic semiconductor materials. To improve their properties, precise prediction of electronic properties and control of the micro-structure of the materials are necessary. The micro-structure refers to all crystal defects (lattice defects), including grain boundaries, pores, precipitates, dislocations, and stacking faults. Figure 2 is a conceptual diagram of the structure and organization of ceramics introduced by Yasui, (1982) and applied to micro-structures of FGMs (Hirano, 1995). In the figure, the micro-structures are classified by physical scales. Actual materials consist of complex combinations of these microscopic structures, and the physical properties at the crystal lattice level rarely appear directly as macro properties. Therefore, in material design, theoretical considerations must be made at each physical scale of the microscopic structures of the material, namely, the crystal lattice level, the micro-structure level, and the solid material/device as a whole.
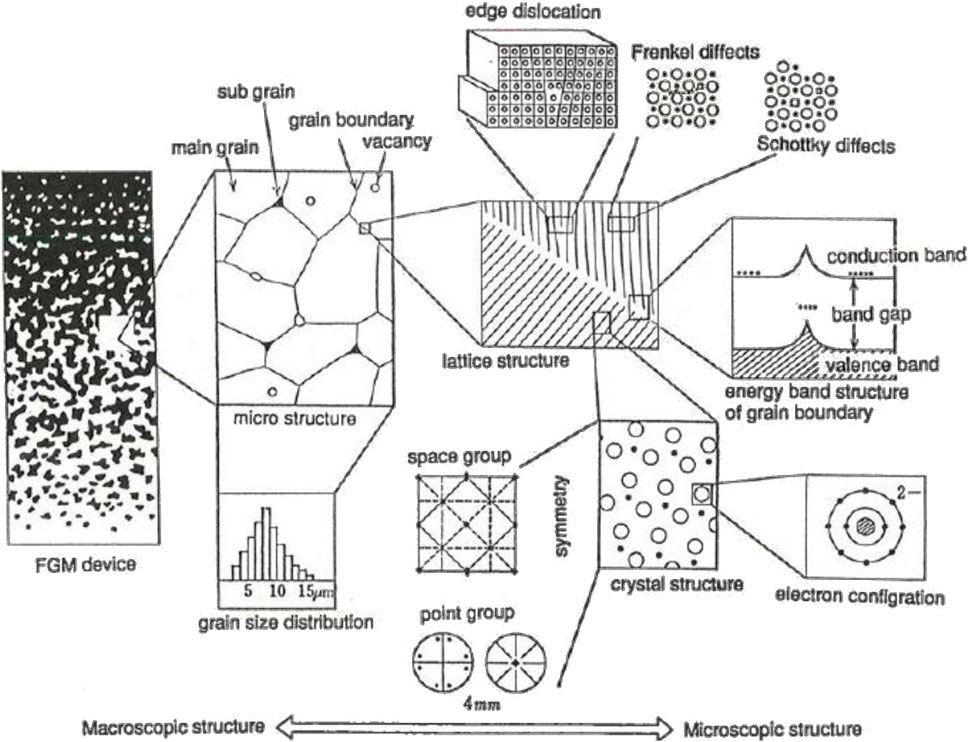
Figure 2. Physical structures of different scales in FGM devices (Hirano, 1995).
For example, TE conversion devices operate under large temperature gradients to generate electricity via the Seebeck effect. Therefore, in addition to evaluating the power generation efficiency of TE materials, it is essentially multi-physics to assess and mitigate thermal stress distributions at the interfaces between electrodes and TE elements, as well as within composite TE materials.
Also, to evaluate the performance of TE devices, it is essential to solve multi-physics phenomena that couple thermal and electrical transport processes. Figure 3 shows the analysis model of TE EC-FGM module.
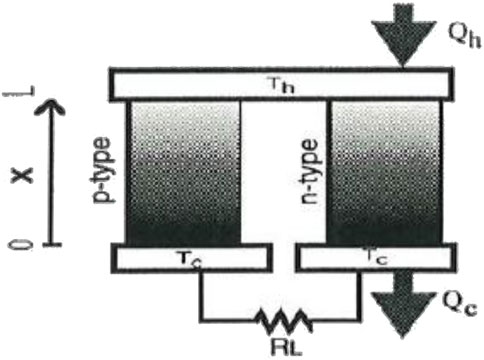
Figure 3. Analysis model of thermoelectric FGM module (Hirano, 1995).
And the set of coupled differential equations derived from the Boltzmann transport equation are shown in Equation 1 (Hirano, 1995), where j denotes the electric current density, q the heat flux, ф the electric potential, T the temperature, σthe electrical conductivity, α the Seebeck coefficient, and κ the thermal conductivity (lattice κL + electronic κe).
3 Current technologies and methods
Developing and optimizing FGMs rely heavily on advanced technologies and methods. This section explores the key techniques currently employed in the modeling and design of FGMs.
3.1 Finite element method (FEM) and its applications
FEM allows for the simulation of complex geometries and material behaviors by discretizing the material into smaller elements. In the initial phase of FGMs development, inverse design procedures based on analytical solutions under steady-state conditions were employed, particularly for infinite plates and axisymmetric cylindrical geometries, to optimize the graded compositional distribution (Hirano et al., 1990). However, in order to validate these designs against experimental evaluations of synthesized FGMs, unsteady thermal conduction and thermal stress analyses were subsequently performed using two-dimensional finite element models that incorporate edge effects (Kawai et al., 1992; Teraki et al., 1992). Also, the thermo-elasto-plastic behavior of FGMs under thermal loading and the evaluation of residual stresses after unloading were evaluated (Arai et al., 1993). Since then, FEM has become a widely adopted tool for the analysis and design of FGMs.
Suresh and Mortensen published a book of comprehensive review on FGMs (Suresh and Mortensen, 1998), which includes the fundamentals of processing and thermomechanical response of graded metals and metal/ceramic composites, covering broad range of topics including process metallurgy, composite synthesis, the mechanics and micromechanics of composites, and fracture mechanics. Moreover, it includes one chapter on FEM describing fundamentals of FEM for FGMs, thermal stress analysis, boundary conditions and modeling, stress-strain behavior and fracture mechanics, and practical applications and validations (Suresh and Mortensen, 1998). On the other hand, Reddy published a paper on the development of FEM elements tailored for multilayered plates with graded compositions (Reddy, 2000), which has significantly enhanced the accuracy of FGM modeling and evaluation along with the integration of advanced FEM techniques such as adaptive meshing and multi-physics simulations.
3.2 Multi-scale modeling with homogenization
Multi-scale modeling is a powerful approach that integrates information across different length scales, from the microscale to the macroscopic level. This method allows for a comprehensive understanding of how micro-structural features influence the overall properties of FGMs. While Homogenization Method (Bendsoe and Kikuchi, 1998) was developed for modeling periodic micro-structures and widely implemented in commercial FEM solvers such as Ansys and ABAQUS, a different approach has been proposed for thermal stress-relaxation type FGMs (Rhee, 2007). In this approach, the geometric characteristics of the microcells are explicitly parameterized within each finite element, and the graded microscale problems are solved using a non-periodic homogenization method. Then, the results were incorporated into the macroscale FEM stiffness matrix (Rhee, 2007).
3.3 Micro-mechanics and fracture analysis
As mentioned above, micro-mechanics analyses focused on understanding the relationship between the micro-structural features of FGMs and their macroscopic properties. On the other hand, a theoretical investigation based on fracture mechanics was conducted by Erdogan for the first time to evaluate the fracture strength of FGMs in the presence of initial micro-cracks introduced during fabrication (Erdogan and Wu, 1997). In this study, a plane elasticity problem was formulated for FGMs in which the Young’s modulus varies continuously in the thickness direction. Surface-perpendicular cracks were introduced to model both edge and embedded cracks. Under three distinct loading conditions, the stress intensity factors (SIF) were theoretically derived. Furthermore, the crack opening displacement (COD) and stress distributions were analyzed to clarify the influence of FGMs gradation on fracture behavior (Erdogan and Wu, 1997). This work has provided a theoretical foundation for the fracture-safe design of FGMs. Furthermore, a toughness enhancement design utilizing stress-induced phase transformation based on micro-mechanical analysis was also proposed for metal–ceramic FGMs (Tukamoto, 2017).
The effect of material property variation on ductility and fracture strain in FGMs was investigated using FEM and the Gurson-Tvergaard-Needleman (GTN) model (Shahzamanian et al., 2020), which is strain-controlled for void nucleating. The material properties of FGMs in the tensile tests are represented by a power low distribution in the thickness direction. The ductility and fracture strain changes with gradation index. The development of stress triaxiality slows down in FGMs, and the total void volume fraction is reduced (Shahzamanian et al., 2020). Figure 4 shows the comparison of thermal stress distributions in conventional thermal barrier coating and FGMs (Shahzamanian et al., 2020).
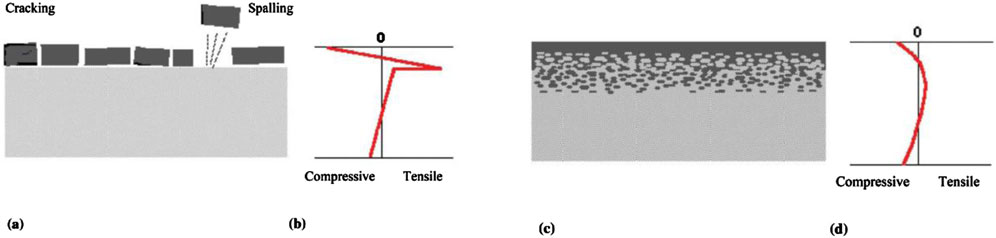
Figure 4. Comparison between a conventional and FGM thermal barrier (Shahzamanian et al., 2020). (a) Conventional thermal barrier coating, (b) Thermal stress distribution, (c) FGM thermal barrier coating, (d) Thermal stress distribution.
To support the design and lifetime prediction of thermal barrier coatings (TBCs) using FGMs in gas turbine blades and high-temperature structural components, thermal fracture behavior analyses focusing on structures with pre-existing edge cracks and multiple internal cracks arranged to imitate a curved interface have been reported recently (Petrova and Schmauder, 2021). Another new method to evaluate fracture mechanism of FGM was also introduced recently, which is based on extended FEM (XFEM) developed by Belytschko (Moes et al., 1999). It is reported that XFEM can analyze crack propagation without remeshing, and capture crack paths influenced by property gradation, ensuring high accuracy in Stress Intensity Factor (Sinha and Pamnani, 2025).
Another application of FGMs was recently reported, in which polymeric laminated composite materials including polymer FGMs are investigated numerically by FEM for improving the tribological behavior and experimentally verified (Nowler et al., 2025). By designing a gradual variation in material properties across the laminate thickness, the authors demonstrate reduced wear rates, lower friction coefficients, and improved stress distribution. The study includes FEM modeling and tribological testing, showing that FGM-based laminates outperform conventional ones under sliding contact conditions (Nowler et al., 2025).
3.4 Transport properties in energy conversion materials
As explained in historical background, fundamental research on the Energy Conversion FGMs (EC-FGMs) was started to improve the conversion efficiency of energy conversion materials (Hirano et al., 1994; Hirano, 1995). In this situation, precise estimation of thermal and electronic transport properties and tailoring of micro-structures were required. For the estimation of the transport properties, different scales of physical structures, ranging from lattice level crystal structure, grain level micro-structure and macro scale device structure are considered. Several estimation methods of the material properties for the design of EC-FGMs were considered. As one of the energy conversion materials, thermoelectric (TE) materials were investigated, and models were presented for the transport properties of heavily doped TE semiconductors (Hirano et al., 1994; Hirano, 1995; Hicks and Dresselhaus, 1993; Whitlow and Hirano, 1995; Nishio and Hirano, 1997; Chen et al., 2003). The dimensionless figure-of-merit (ZT) plays a decisive role of TE materials as the critical measure of the energy conversion performance. Equation (2) defines ZT by several material parameters, where α, σ, κL, κe, and T are the Seebeck coefficient, electrical conductivity, lattice thermal conductivity, electronic thermal conductivity, and absolute temperature, respectively.
To increase ZT the use of quantum well was proposed to increase the product α2σ by Hicks and Dresselhaus (Hicks and Dresselhaus, 1993), which introduces quantum confinement effects that modify the electronic density of state leading to an increase in the Seebeck coefficient and a reduction in thermal conductivity.
Thereafter, the carrier energy filtering concept applied to Super Lattice structure was firstly proposed in the EC-FGMs project (Whitlow and Hirano, 1995). The concept was improved more precisely to include ionized impurity (electron and hole) carrier energy filtering and phonon (acoustic and optical) scattering into the theoretical approach for the optimization of the parameters α2σ, κL andκe influencing the charge-carrier energy spectrum and phonon scattering, through structural changes or the material and the scattering interactions (Nishio and Hirano, 1997). The theoretical calculation results were shown that phonon scattering effects are quite dominant rather than ionized impurity scattering (Nishio and Hirano, 1997).
Chen and Dresselhaus reported a comprehensive review on the advances in the field of TE materials (Chen et al., 2003). They focused on two major areas as shown below and proposed so-called Phonon Engineering, which aims to decrease the lattice thermal conductivityκL by means of phonon scattering in addition to reduce the electronic thermal conductivityκe due to electron scattering (Chen et al., 2003).
3.4.1 Nanostructured materials
1) Nano-structured Materials: Control of electron and phonon transport properties through the use of nano-structures such as quantum wells, superlattices, quantum wires, and quantum dots.
2) Enhancement of energy conversion efficiency by engineering the electronic band structure and density of states.
3) Reduction of thermal conductivity by promoting phonon scattering and interfacial reflection.
3.4.2 Bulk materials
1) Realization of the “phonon-glass electron-crystal” (PGEC) behavior through the synthesis of new materials with complex crystal structures.
2) Development of materials with high thermoelectric performance with ZT approaching 1.5 at high temperatures, and active research aiming for ZT > 1 near room temperature.
4 Recent research trends
The field of FGMs has seen significant advancements in recent years, driven by the integration of new technologies and innovative approaches. Also, general micro-structure modeling and design technologies have been widely studied and several new concepts have emerged. This section highlights some of the key trends in general micro-structure modeling and design technologies.
4.1 Applications of deep learning (DL) and artificial intelligence (AI)
AI and Deep Learning (DL) have become powerful tools for the modeling of micro-structures. For example, a novel design framework was constructed by integrating two types of neural networks. Deep Convolutional-Generative Adversarial Network (DC-GAN), which generates candidate micro-structures that satisfy geometric constraints, and Convolutional Neural Network (CNN), which serves as a surrogate model to learn the relationship between microstructural geometry and its corresponding physical properties (e.g., compliance tensor) (Tan et al., 2020). By combining these networks into a unified “design network,” inverse design becomes feasible, enabling the efficient generation of micro-structures that exhibit desired material properties (Tan et al., 2020). Also, application of DL to inverse design of phase separation structure in polymer alloy was reported (Hiraide et al., 2021), in which the micro-structures are dependent on the volume fraction of polymer A and the product of the repulsive interaction and chain length as shown in Figure 5a). In this study, forward process to estimate Young’s modulus from micro-structure image utilized CNN, and inverse design process was done by GAN as shown in Figure 5b) (Hiraide et al., 2021).
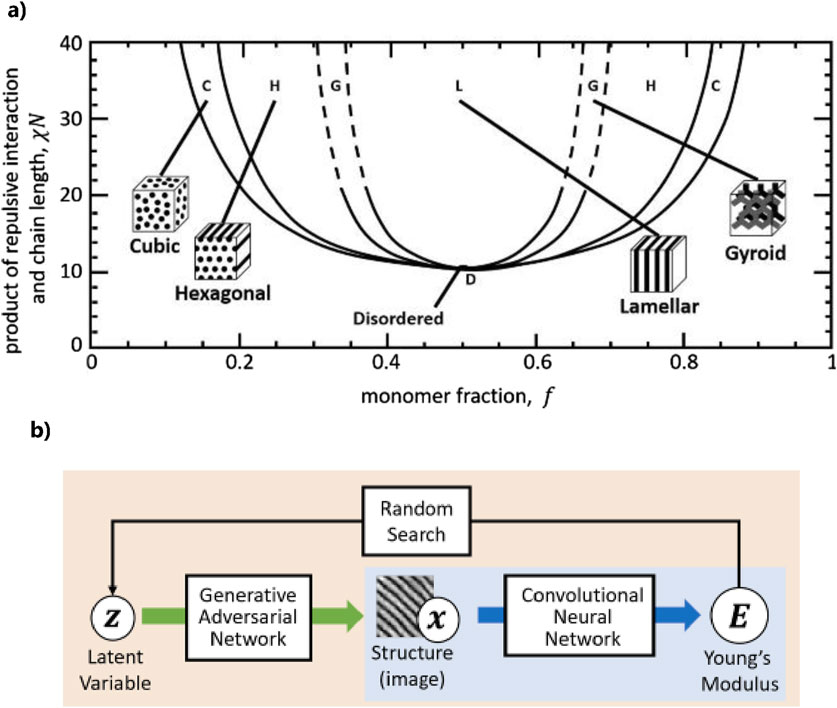
Figure 5. (a) Phase separation structure of polymer alloy (Hiraide et al., 2021) (b) Conceptual diagram of the network (Hiraide et al., 2021).
Another machine learning framework was proposed that emulates the thinking process of metallurgists, with the aim of identifying microstructural features that critically influence material properties (Noguchi et al., 2022). Usual machine learning approaches often lack interpretability due to insufficient understanding of the underlying physical mechanisms and causal relationships. In this work, by mimicking the intuitive design process of human experts, the Vector Quantized Variational Auto-Encoder (VQ-VAE) seeks to automatically extract key structural features without relying on explicit physical models, and PixelCNN enables highly accurate structure generation and reconstruction as shown in (Figure 6) (Noguchi et al., 2022). The target material system is artificially designed dual-phase steel, and the optimization focuses on fracture-related properties (Noguchi et al., 2022). The same authors also presented on Baysian inverse inference of material properties from micro-structure images (Noguchi and Inoue, 2024).
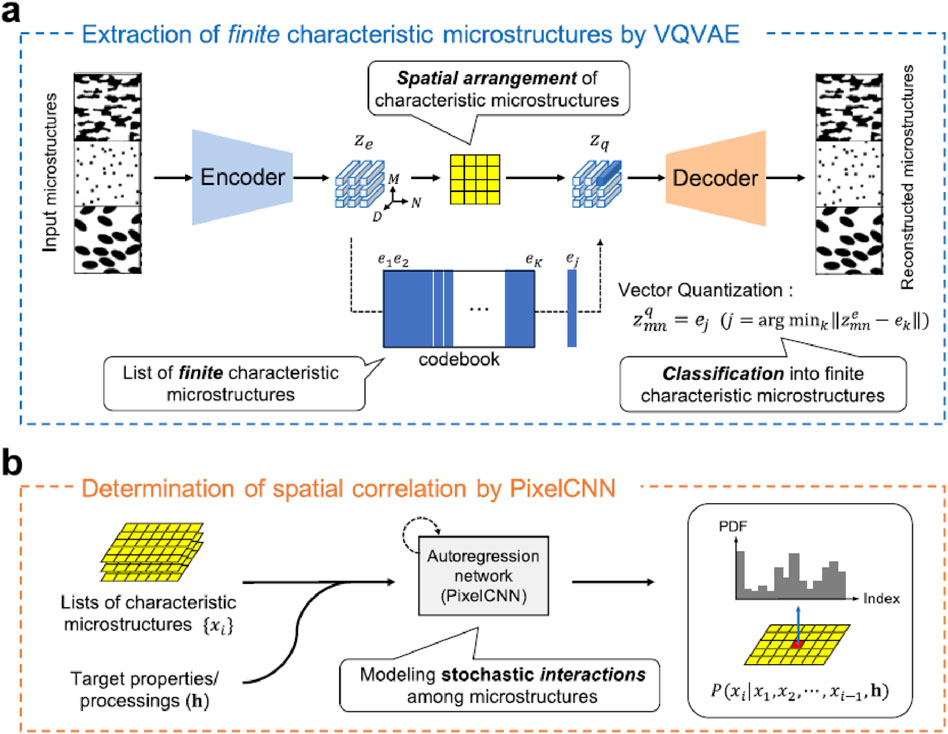
Figure 6. Application of deep learning for identification of micro-structures (Noguchi et al., 2022).
A novel framework for predictive micro-structure image generation was presented (Azqadan et al., 2023) utilizing Denoising Diffusion Probabilistic Models (DDPMs) (Ho et al., 2020). By leveraging the iterative denoising process inherent to DDPMs, the proposed method enables the synthesis of high-fidelity micro-structure images conditioned on material-specific parameters such as composition, processing history, and target properties (Azqadan et al., 2023). The generated images exhibit statistically consistent features with experimentally observed micro-structures, including grain morphology and phase distribution. This approach offers a promising solution to the inverse design problem in materials science, facilitating the generation of plausible micro-structures from desired macroscopic properties (Azqadan et al., 2023). Figure 7 shows the whole processes of proposed system with DDPM.
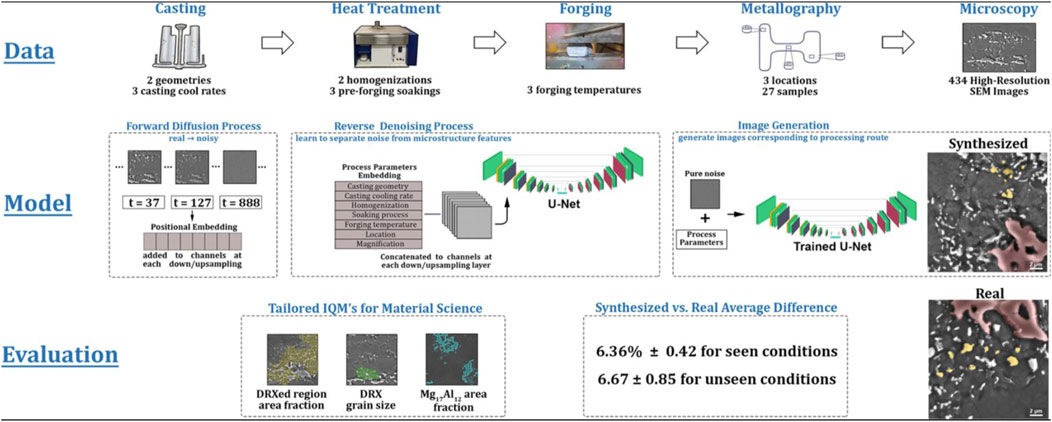
Figure 7. High-fidelity Micro-stracture image Generation by DDPM (Azqadan et al., 2023) (open access).
More comprehensive survey for AI-driven approaches for multi-scale modeling was reported recently (Peng et al., 2025), which includes parameterized micro-structures and FEM homogenization with meshes based on diffuse interface representation and DL based surrogate model training. With the trained surrogate models, micro-structure optimization or inverse design of micro-structure can be efficiently executed (Peng et al., 2025). It also introduced MCRpy (Seibert et al., 2022), an open-source Python framework designed for the characterization and reconstruction of micro-structures in materials science displayed in Figure 8. Micro-structures, such as grain boundaries, pores and phases, play a critical role in determining the macroscopic properties of materials. MCRpy provides a modular and extensible platform for analyzing micro-structural features using statistical descriptors and for reconstructing synthetic micro-structures that match desired characteristics. The framework supports integration with machine learning models and optimization algorithms, enabling data-driven materials design and analysis (Seibert et al., 2022).
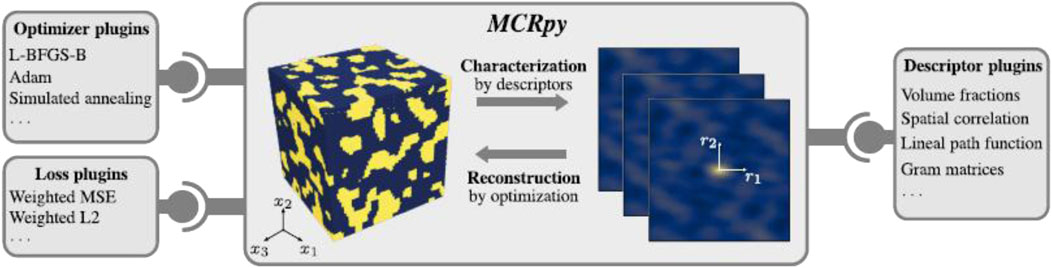
Figure 8. MCRpy: Micro-structures characterization and reconstruction framework (Seibert et al., 2022).
4.2 Utilization of transformer models
The Transformer is a deep learning architecture introduced by Vaswani et al., in 2017 (Vaswani et al., 2017), which has since become foundational in a wide range of machine learning applications, particularly in natural language processing (LLM), computer vision (ViT), and scientific domains such as Materials Informatics (most famous example is AlphaFold (Jumper et al., 2021)). The Transformer architecture is composed of two primary modules: the encoder and the decoder. The encoder processes the input sequence and generates a contextualized representation, while the decoder utilizes this representation to generate the output sequence. A key innovation of the Transformer is the self-attention mechanism, which allows the model to dynamically weigh the importance of different elements in the input sequence. This mechanism is further enhanced by multi-head attention, which enables the model to attend to information from multiple representation subspaces simultaneously. To compensate for the lack of inherent sequential structure, positional encoding is added to the input embeddings, allowing the model to incorporate order information (Vaswani et al., 2017).
An innovative approach to the design of architected materials directly from natural language descriptions was proposed (Yang and Buehler, 2021). The authors employed a transformer-based neural network architecture, combining CLIP and VQGAN, to generate material structure images from textual prompts (e.g., “a regular lattice structure of steel”), which were subsequently used to construct 3D models and to fabricate them via 3D printing realizing a “Words to Matter” pipeline (Yang and Buehler, 2021). This approach introduced a novel design paradigm that differs fundamentally from conventional Computer Aided Design (CAD) or numerical design methods by enabling intuitive linguistic expressions to be directly translated into material architectures (Yang and Buehler, 2021).
A hybrid algorithm with Transformer and CNN encoders, called as CS-Net, for micro-structure image segmentation in materials science was proposed (Alrfou et al., 2023), which also utilized Transfer Learning for models pre-trained specifically on microscopic images achieved higher segmentation accuracy as compared to those trained on natural image datasets (Alrfou et al., 2023). Figure 9 shows the Encoder-Decoder architecture and the test data.
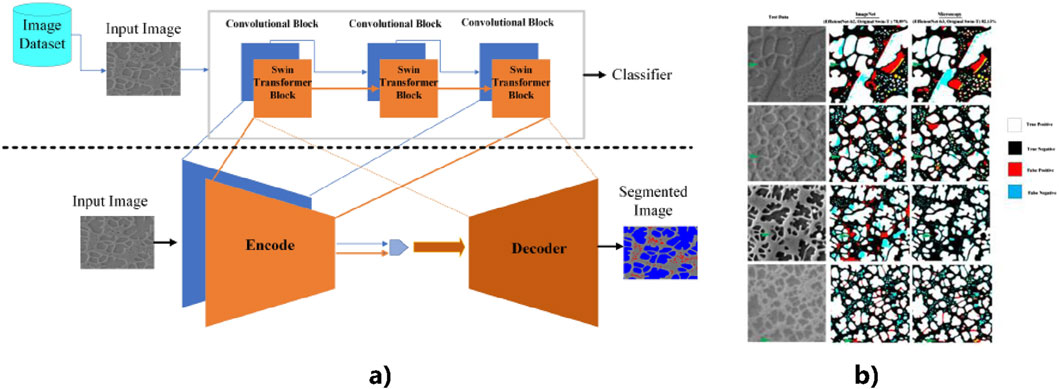
Figure 9. (a) Encoder-Decoder architecture (Alrfou et al., 2023) (b) Test Data, ImageNet Data, Microscopy (Alrfou et al., 2023) (CNN + SwinTransformer).
The first large-scale benchmark on generative design of inorganic materials using transformer-based language models was presented (Fu et al., 2023), including GPT, BART, and RoBERTa Language models, that have demonstrated success in natural language processing and molecular design, are applied to the generation of inorganic material compositions, and their performance is evaluated in terms of chemical validity, novelty, and property control. The authors trained and compared seven transformer models using composition data extracted from large-scale materials databases such as ICSD, OQMD, and the Materials Project (Fu et al., 2023). Figure 10 shows the candidate new structures discovered by MT-GPT2 model with zero e-above hull (Fu et al., 2023).
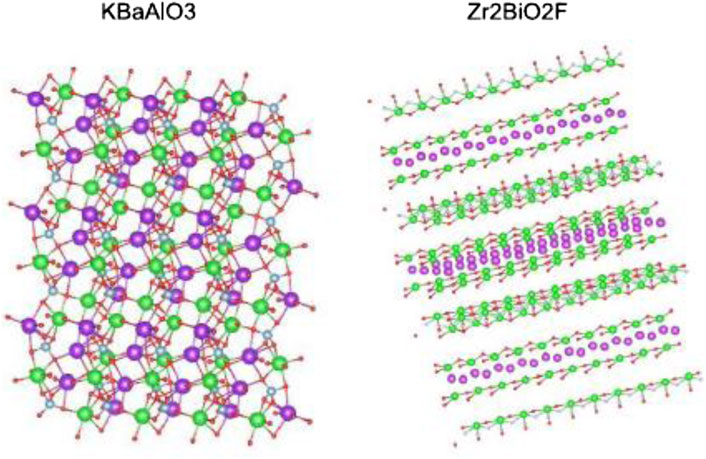
Figure 10. Candidate new structures discovered by MT-GPT2 model with zero e-above hull (Fu et al., 2023).
A Transformer-based language model developed for the prediction of polymer properties was proposed recently (Xu et al., 2023). Traditional approaches to evaluating polymer characteristics often rely on costly and time-consuming experiments or simulations. This study introduces a novel methodology that leverages the Transformer architecture to directly predict polymer properties from their sequences. The model employs a chemically-informed tokenizer to represent polymer structures and is pretrained using masked language modeling (MLM) on a large corpus of unlabeled polymer sequences. TransPolymer demonstrates superior performance across multiple downstream property prediction tasks. Figure 11 shows the key architecture of TransPolymer (Xu et al., 2023).
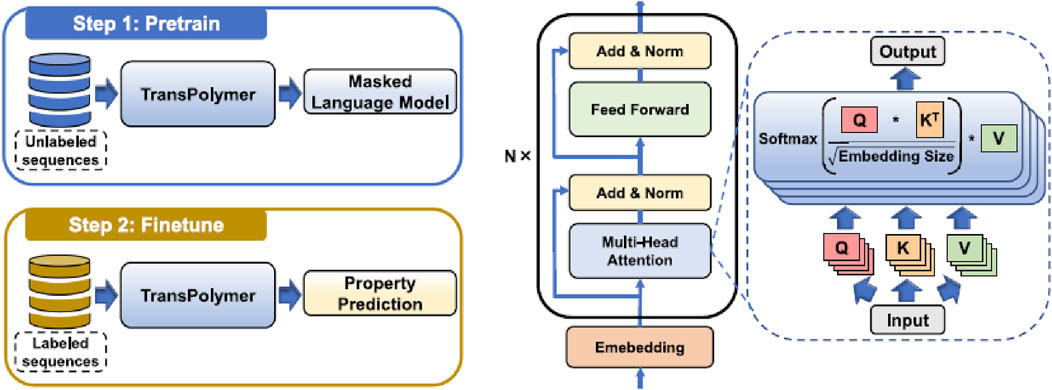
Figure 11. The Key Architecture of TransPolymer: Pretraining and Finetuning (Xu et al., 2023) (open access).
4.3 New material design and manufacturing methodologies
4.3.1 Additive manufacturing (AM)
Innovative material design and manufacturing methodologies are being developed to enhance the performance and functionality of FGMs. Additive manufacturing (AM), also known as 3D printing, has emerged as a transformative technology in this field (Haghdadi et al., 2021; Alagha et al., 2021; Sanjeeviprakash et al., 2023). Especially, after the invention of advanced manufacturing techniques including Selective Laser Melting (SLM), Binder Jetting (BJ) and Direct Energy Deposition (DED) have been established, AM can allow for the precise control of material composition and structure enabling the fabrication of Shape Memory Alloy (SMA) parts with complex geometries and tailored properties (Alagha et al., 2021). Figure 12 depicts the whole AM process for SMA parts (Alagha et al., 2021).
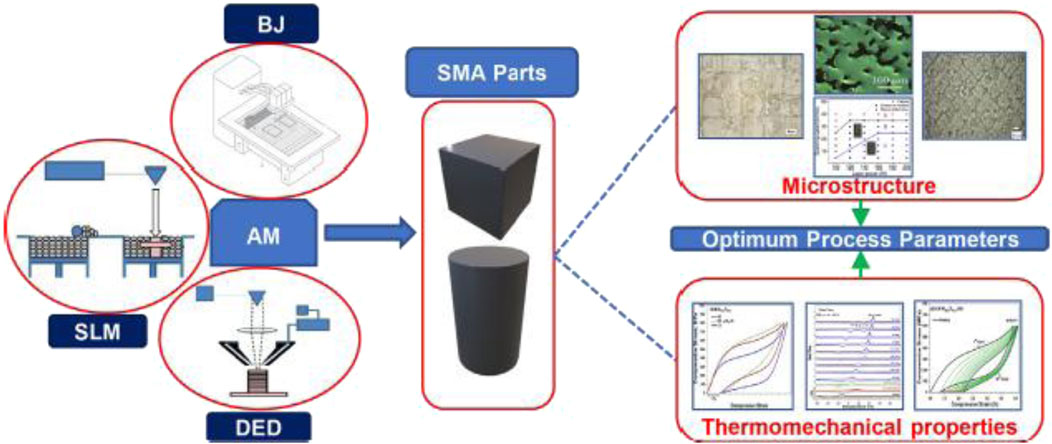
Figure 12. Whole AM process for Shape Memory Alloys (SMA) parts (Alagha et al., 2021) (open access).
Because AM processes for FGMs using Direct Laser Deposition (DLD) are quite complicated, the quality monitoring is required for commercialisation. Novel monitoring method for chemical composition and process regimes for FGMs was proposed using Acoustic Emission Mic and Optical Emission Spectroscopy (OES) sensors. Figure 13 shows the application of AI in monitoring AM DLD processes (Wasmer et al., 2023). The standard machine equipments are in grey, the sensors and acqisition PC are in green, and blue arrows reprisent the digital cables used for data transport (Wasmer et al., 2023).
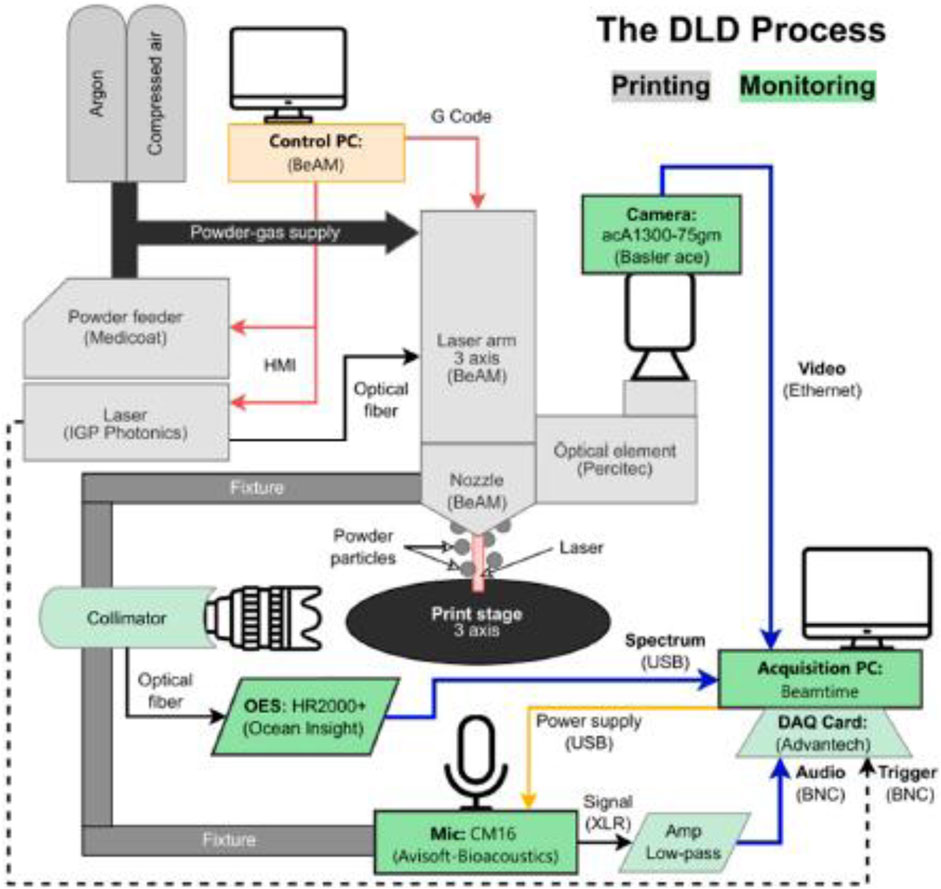
Figure 13. Application of AI in monitoring AM DLD process (Wasmer et al., 2023) (open access).
A case study was reported on the multi-disciplinary approach integrating design, manufacture and evaluation of Metal-based FGMs using multi-feed Wire-Arc Additive Manufacturing (WAAM) to create FGM parts with tailored properties (Silva et al., 2024). This method allows for the layer-wise deposition of different materials (Al-Cu), resulting in a smooth gradation of properties. The use of topology optimization (TO) and image-based characterization further enhances the design and performance of these FGM parts (Silva et al., 2024). In Figure 14, the distributed loads Q generate torque, and beam is subject to pure bending (Silva et al., 2024).
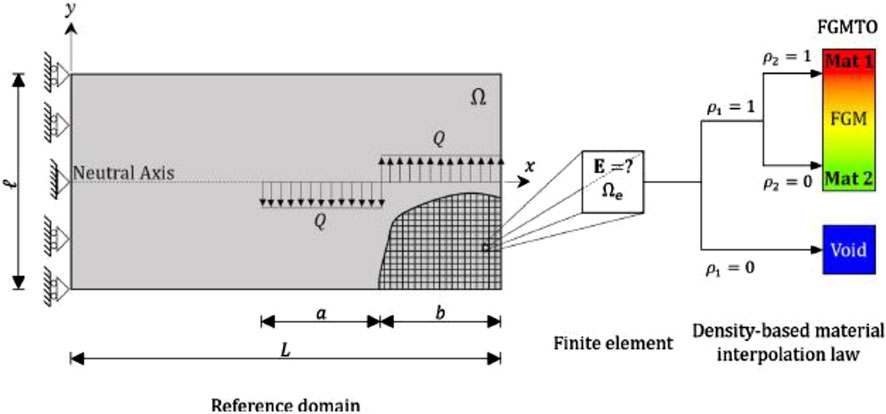
Figure 14. Numerical model for Two-dimensional (half) beam of AM FGMs (Silva et al., 2024).
Another comprehensive review on the recent advancements and challenges in AM FGMs was reported, in which conceptual approaches for AM FGMs design, various manufacturing techniques and the materials employed in their fabrication using AM technologies are explained (Alkunte et al., 2024a). Moreover, many different applications covering structural engineering, automotive, biomedical engineering, soft robotics, electronics, 4D printing and metamaterials are described (Alkunte et al., 2024a).
4.3.2 Metamaterials (MMs)
The concept of Metamaterials was firstly proposed in 1967 by Russian physicist Victor Veselago through a theoretical study. He described materials possessing properties not found in nature, enabled by artificially engineered structures (Veselago, 1967). Although this theory remained unverified experimentally for several decades, it was not until 2000 that David R. Smith and his colleagues successfully demonstrated a Metamaterial exhibiting a negative refractive index in the microwave regime. Then, Smith and his colleagues patented the concept as Metamaterials (Smith et al., 2009).
An overview of Metamaterials (MMs) designed for the control of elastic waves and vibrations was presented (Dai et al., 2022). Emphasis was placed on acoustic MMs, including both passive and active types, and their respective mechanisms for wave manipulation. Passive MMs, such as phononic crystals and locally resonant structures, were shown to exhibit band gap formation and wave attenuation capabilities, while active MMs enable dynamic tuning of wave propagation characteristics through external stimuli (Dai et al., 2022). This paper highlighted advanced design methodologies such as topology optimization, bio-inspired architectures, and fractal geometries, which contribute to enhanced wave control performance (Dai et al., 2022). AM techniques are discussed as key enablers for fabricating complex multi-material and multi-scale structures. Applications span across aerospace, automotive, civil engineering, and biomedical domains, where vibration isolation, noise reduction, and wave steering are critical (Dai et al., 2022).
A study was reported on the design and fabrication of biomimetic MMs using 3D printing technologies (same with AM), focusing on structures with graded porosity and tapered topology (Zhang et al., 2023). Inspired by natural materials such as bone and plant stems, the proposed MMs exhibit enhanced mechanical performance through spatial variation in porosity and geometry (Zhang et al., 2023). The integration of bioinspired design principles with AM enables the creation of lightweight, mechanically robust structures suitable for applications in biomedical implants, aerospace components, and soft robotics (Zhang et al., 2023). Figure 15 shows several different morphologies with graded porosity and geometry.
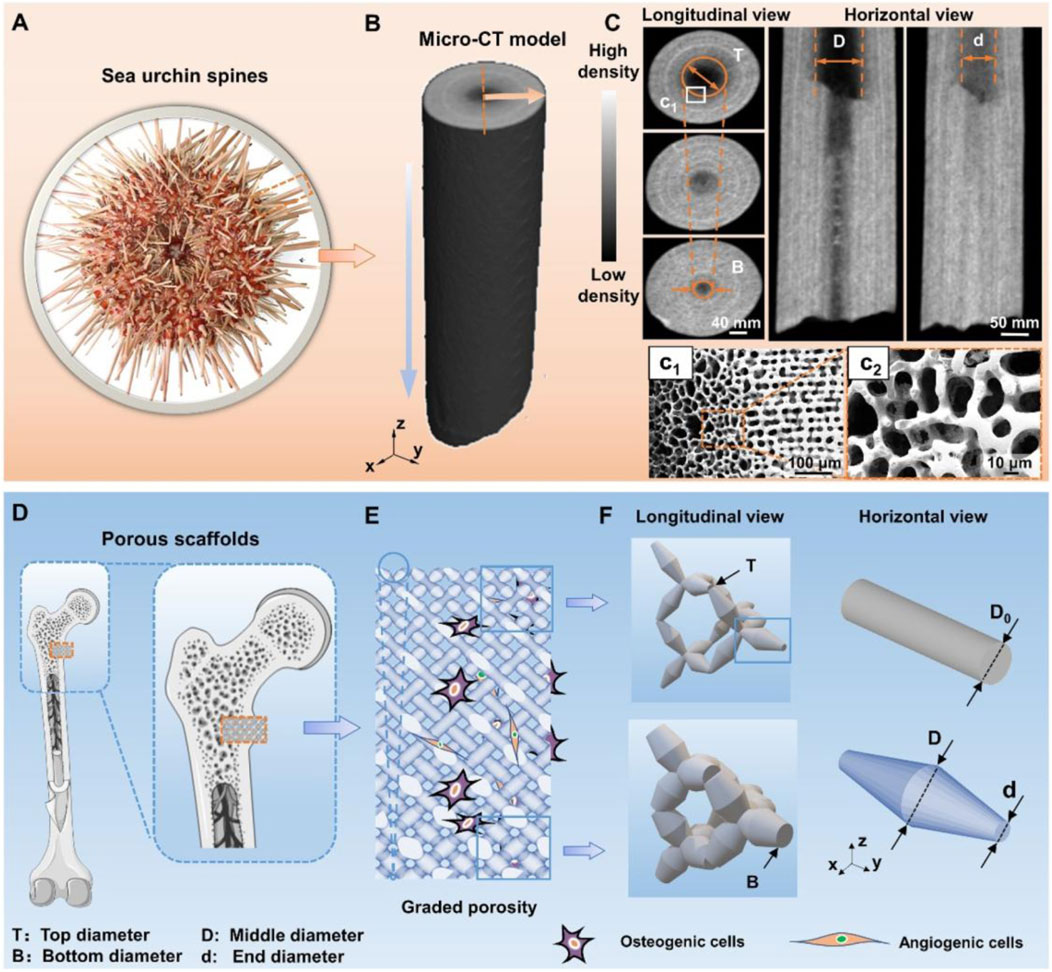
Figure 15. Topological morphologies of sea urchin spine and its biomimetic scaffolds (Zhang et al., 2023). Sea urchin spines’ needle-like appearance and internal architecture of graded porosity. (A) The optical image shows the natural features of the sea urchin spine. (B) Micro-computed tomography (CT) images show internal graded porosity in horizontal view and longitudinal views. (C) SEM images present the delicate internal morphologies in (c1-c2) sectional views. (D) Schematic diagram of the position of porous scaffolds within the implant. (E) Biomimetic graded pentamode-based scaffolds. (F) Geometrical features of the graded density from longitudinal view and the tapering strut topology compared with the uniform struts in horizontal view (Zhang et al., 2023). (open access).
Similarly, Functionally Graded Lattices (FGLs) produced by AM were investigated in view of the design, fabrication, and performance (Noronha et al., 2023). FGLs are engineered structures with spatially varying properties—such as density, stiffness, and geometry—to achieve tailored mechanical responses as shown in Figure 16. The study explores various design strategies, evaluates mechanical behavior under different loading conditions, and discusses deformation mechanisms (Noronha et al., 2023). It also highlights the broad application potential of FGLs in fields such as biomedical engineering, aerospace, and energy absorption systems. The insights provided will guide future development of high-performance, multifunctional lattice materials (Noronha et al., 2023).
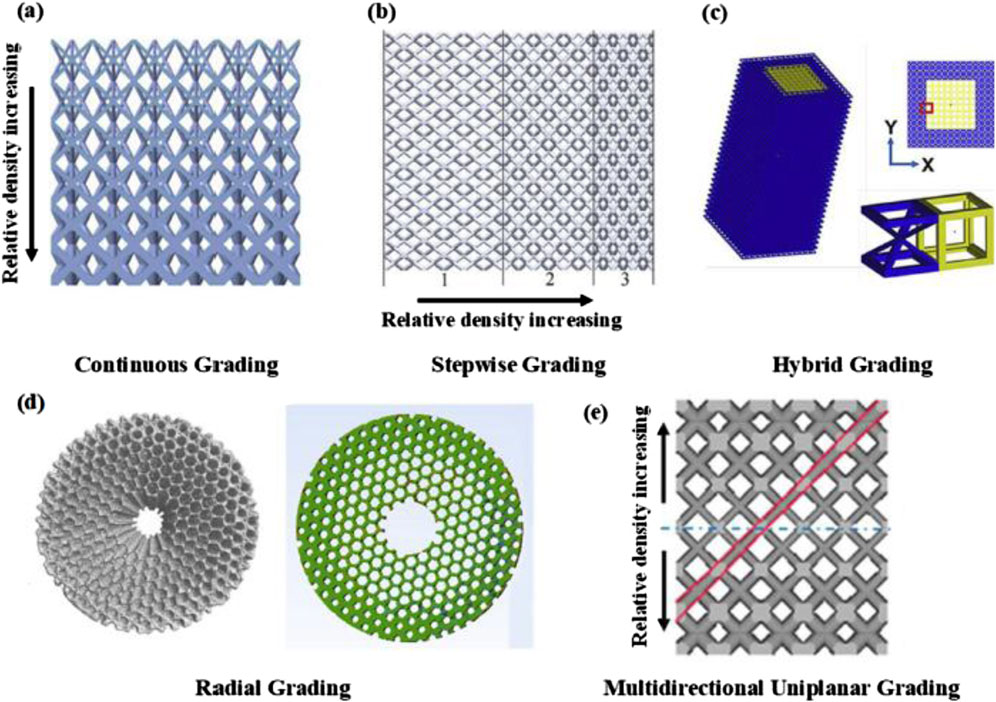
Figure 16. Different grading patterns in functionally graded lattices (FGLs) (Noronha et al., 2023).
Recently, a comprehensive overview on Functionally Graded Metamaterials (FGMMs) including acoustic MMs and FGLs was presented in relation to AM. It covers the relevant technologies applied in the fabrication and design processes, and the theoretical models are mentioned for FGMMs, in addition to related simulation methods utilizing several commercial solvers (Alkunte et al., 2024b).
4.3.3 Lattice and micro-structures improving energy conversion efficiency
In the previous section, FGMMs including FGLs are explained, which are basically designed and optimized to address structural challenges such as weight reduction, relaxation of high thermal stresses and mechanical reinforcement. In this section, however, we shift our focus to efforts aimed at enhancing TE performance, specifically in relation to crystal-level Lattice structures and micro-structures in TE materials. Therefore, in this section atomic-scale nano-structures are investigated in view of inorganic crystal structures or molecules for the determination of intrinsic physical properties of materials.
In relation to crystal lattices and micro-structures for TE materials, the material properties that affect the performance of TE materials were expressed as a hierarchical structure. Figure 17 shows detailed material and transport descriptors (Urban et al., 2019). For example, as expressed in Equation 2, thermal conductivity is comprised with lattice thermal conductivity κL and electronic thermal conductivity κe. And the lattice thermal conductivity is dependent on phonon group velocity, mean free path and specific heat, and so on. Finaly, κL is determined by Elastic constant, Defects, Grain boundary and Anharmonicity.
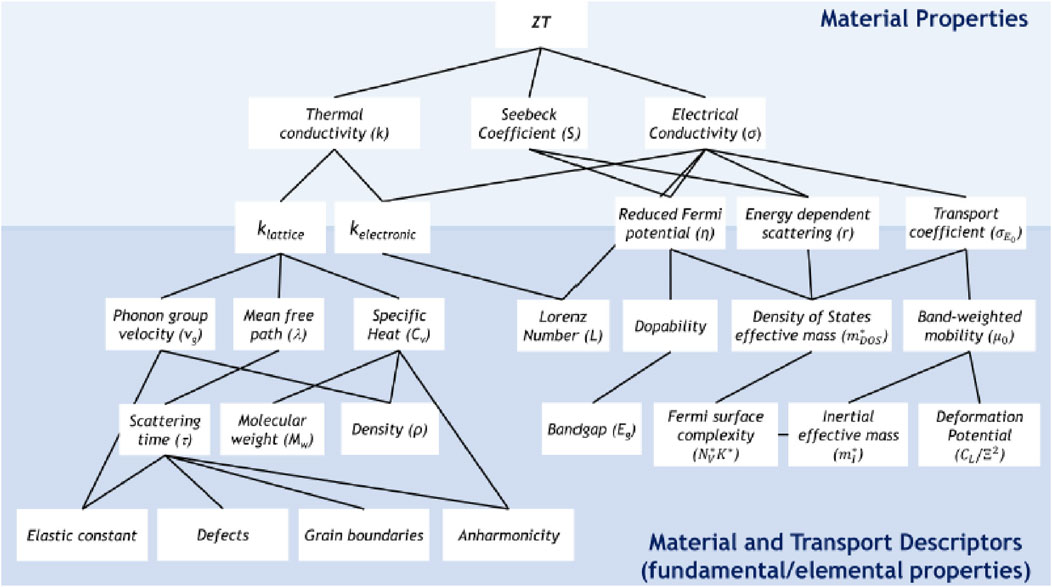
Figure 17. Hierarchical structure for detailed material and transport descriptors (Urban et al., 2019).
For example, Grain boundary effect on κL was theoretically investigated early on the TE properties of granular semiconductors (Narducci et al., 2012). Energy filtering is a mechanism that enhances the Seebeck coefficient by selectively scattering low-energy carriers while allowing high-energy carriers to pass through. However, potential barriers formed at grain boundaries or within nanostructures can induce carrier localization, which may reduce carrier density and consequently lower electrical conductivity. The authors demonstrate that randomly distributed barriers can simultaneously induce both energy filtering and localization. By incorporating quantum tunneling effects into the theoretical model, they showed that an increase in doping concentration can lead to an enhancement in the power factor. Figure 18 shows Energy Filtering on Grain Boundaries in polycrystalline materials (Narducci et al., 2012).
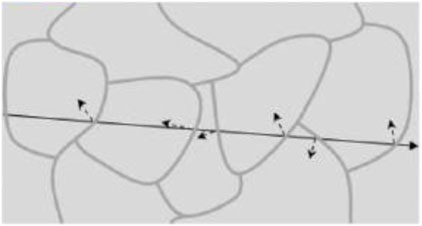
Figure 18. Energy filtering on grain boundary (Narducci et al., 2012).
Then, in recent years, this research field has become more actively studied. Other examples for the enhancement of TE properties by application of point defects were presented (Pan et al., 2015; Fu et al., 2017). Also, quite impressive research was reported on the enhancement of power factor by energy filtering effect in hierarchical BiSbTe3, in which the chemical solution synthesis of nanoparticles was proved as useful manufacturing method for the TE materials because the small particle size causes scattering of phonon along the crystal boundaries, effectively allowing the thermal conductivity to be reduced while maintaining the electrical conductivity as shown in Figure 19 (Sabarinathan et al., 2016).
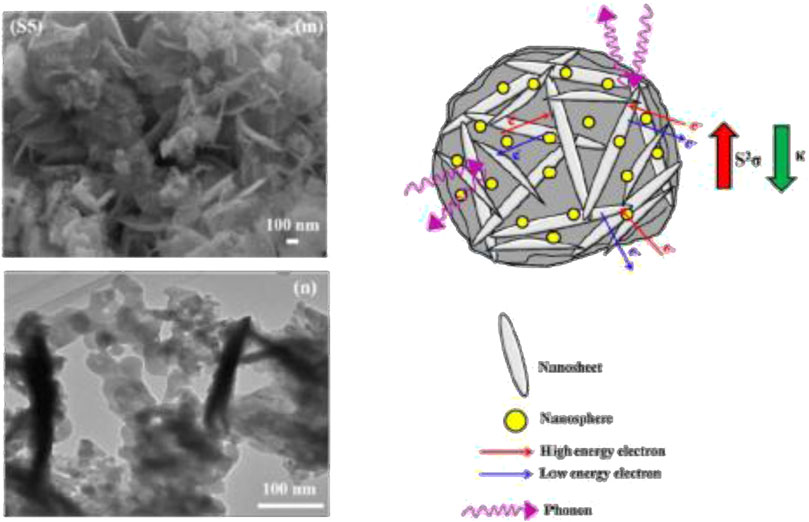
Figure 19. Enhancement of power factor by energy filtering effect (Sabarinathan et al., 2016).
A comprehensive review incorporating new perspectives in this field was reported (Urban et al., 2019). Figure 20 shows the progress of maximum figure of merit (ZT) in bulk inorganic systems up to 2019 displayed in this report. While there have been selective reports of individual materials realizing new record levels of performance (as high as ZT∼2.6) in lab scale SnSe and Cu2Se, no general approach has emerged from these studies. It also explores the potential for enhancing TE performance through novel physical and materials-based approaches in addition to conventional band transport model of TE materials. The authors emphasized the following three areas: 1) wave effects in phonon transport, 2) correlated electron physics, and 3) un-conventional transport in organic materials (Urban et al., 2019).
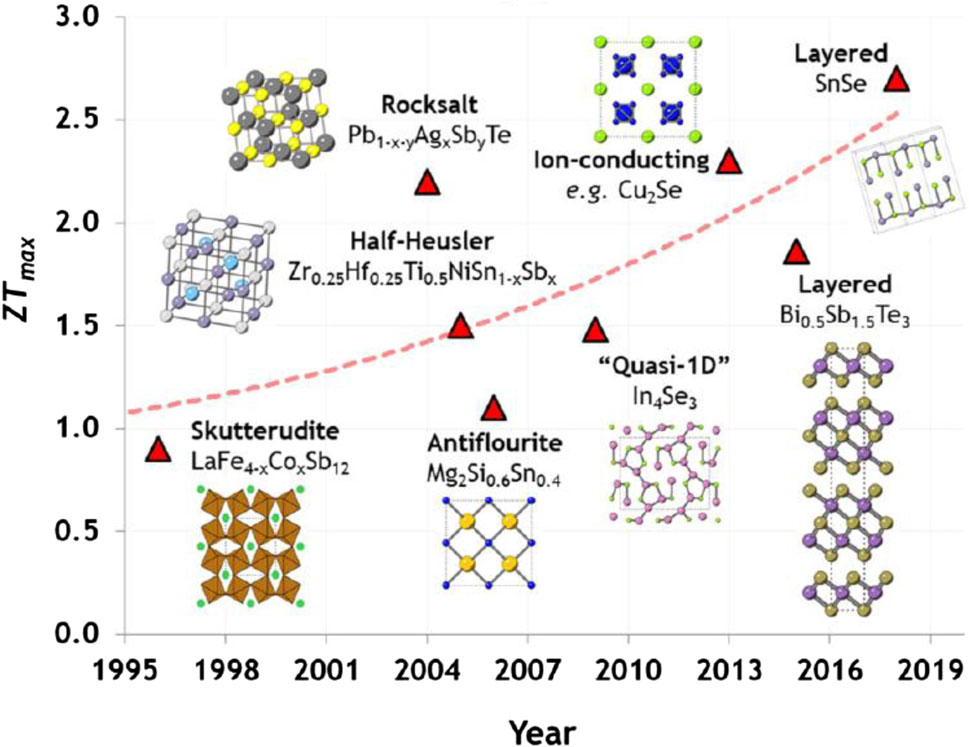
Figure 20. Progress of maximum ZT in bulk inorganic systems achieved over time (Urban et al., 2019).
Previous Figure 17 was also cited from the same report, in which Lorenz number L is expressed as the key factor corelating between electronic thermal conductivity κe and electrical conductivity σ (Urban et al., 2019). When electrons behave as a collective hydrodynamic fluid, charge transport occurs efficiently while thermal energy is dissipated. Such physical behavior enables the decoupling of charge and heat transport, offering a novel mechanism for tuning the Lorenz number (Urban et al., 2019). Furthermore, coherent phonon interference—an emergent wave-based description of phonon transport—has the potential to reduce the lattice thermal conductivity below the lower bound predicted by the classical particle model, without decreasing electronic conductivity. This phenomenon may contribute to the enhancement of the TE figure of merit, ZT (Urban et al., 2019).
The same concept was reported later, in which two types of nano- and micro-structures are explained. Figure 21 illustrates the differences in electron transport between a pristine material and a superlattice structure, highlighting the impact of band structure and energy filtering on carrier dynamics (Neophytou et al., 2020).
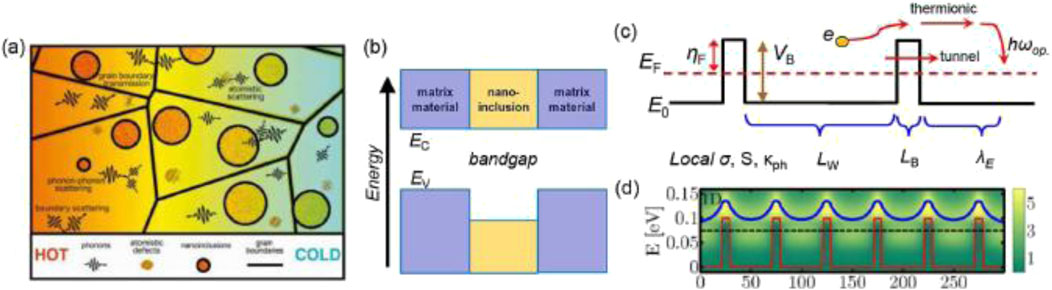
Figure 21. Electron transport between a pristine material and a superlattice structures (Neophytou et al., 2020).
Another experimental verification of enhancing TE efficiency by new method was reported, in which synthetic minerals based on Cu12Sb4S13 (tetrahedrite), a TE material known for its low thermal conductivity and moderate electrical performance (Hu et al., 2021). The authors introduce a novel sublimation-based method to create a porous network within the material, aiming to enhance its TE efficiency. The porous structure is expected to scatter phonons more effectively, reducing thermal conductivity while maintaining or improving electrical conductivity (Hu et al., 2021). Figure 22 illustrates the generation of a porous network during BiI3 sublimation, and representative SEM images of the fracture surfaces of initial and AP 0.7 vol% samples, which show a 3D porous network structure (Hu et al., 2021).

Figure 22. (a) Schemaitc illustration for the generation of porous network during BiI3 sublimation, (b,c) Representative SEM images of the fracture surfaces of initial and AP 0.7 vol% samples (Hu et al., 2021).
Quite recent study was posted, in which classical BiSbTe alloy was processed to optimize phonon and electron transport by new super-gravity-field re-melting method (SGF-RM) (Zhou et al., 2025). Using SGF, the brittle (Bi,Sb)2Te3 alloy undergoes unusual plastic deformation and forms mounts of defects in the micro-structure. As a result, the micro-structure reconstruction and the optimization of carrier concentration were realized simultaneously, resulting in ultra-low lattice thermal conductivity (κL<0.25W/mK) and a record-high figure of merit (ZT > 1.91) in the BiSbTe alloy (Zhou et al., 2025). Figure 23 depicts the synergistically optimizing phonon and electron transport. (A) Shows SGF-RM technology, (B) exhibits bubble movement in melts, and (C) reveals the reconstruction of microstructures after SGF-RM. (D) Explains the process of Te evaporation causing extra holes. (E) Depicts κL of samples before and after SGF-RM. The solid black symbols present the experimental result of Bi0.48Sb1.52Te3.03 alloy before SGF-RM (BST) and the red empty triangles present the corrected experimental values after SGF-RM. The black solid line represents the predicted κL considering the scattering of the Umklapp process, normal process, and point defects (U + N + P). The red solid line represents the predicted κL value considering the additional scattering of dislocations (U + N + P + I + DS). (F) Shows Power factor values as a function of the Hall carrier concentration predicted by the effective mass m* = 1.05m0 and drift mobility μw = 420 cm2/V s at 300 K. (G) zT values of BST and after SGF-RM (Zhou et al., 2025).
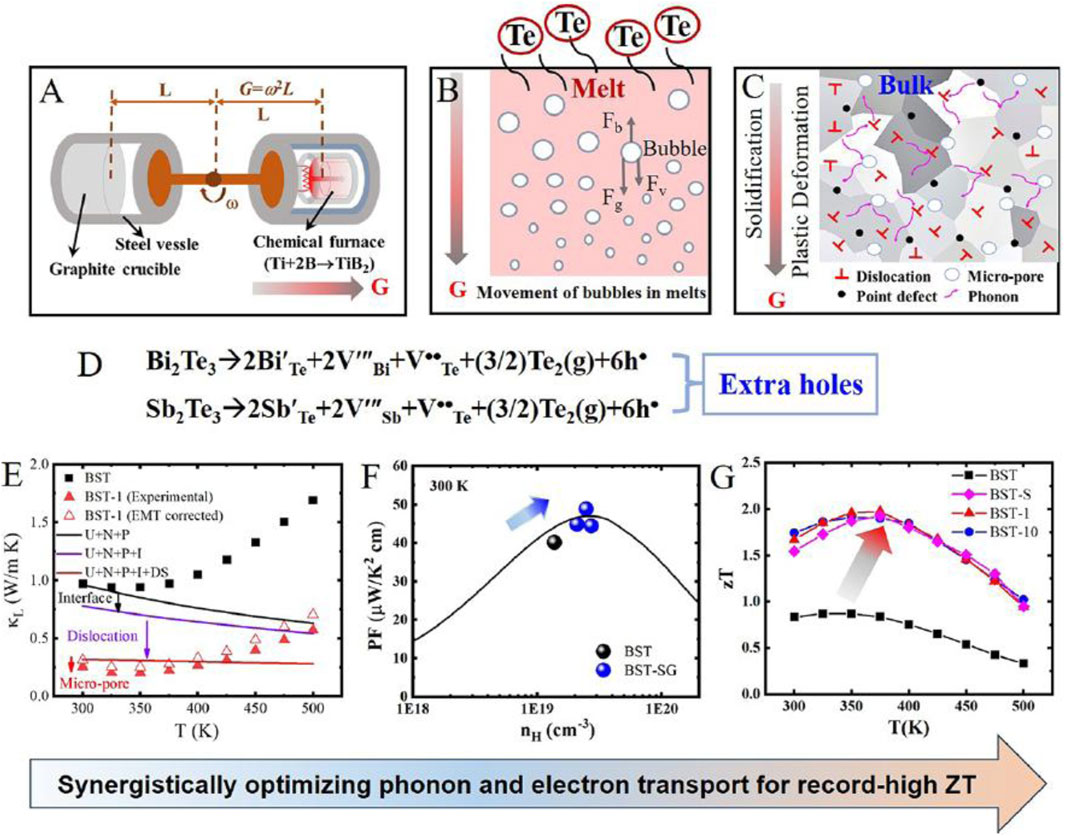
Figure 23. Synergistically optimizing phonon and electron transport for record-high ZT values (Zhou et al., 2025).
Another recent study discussed comprehensive strategies to enhance the TE performance of GeTe-based materials through chemical modulation and defect engineering (Jiang et al., 2025). By introducing specific dopants and controlling intrinsic Ge vacancies, the authors achieved a significant improvement in the figure of merit (ZT), reaching values upto 2.7 at elevated temperatures. The work highlights the synergistic effects of carrier concentration optimization, band structure tuning, and phonon scattering enhancement. Especially, Several phonon scattering mechanisms contributing to the reduction of lattice thermal conductivity κL are compared, including point defect (0D), dislocation (1D), grain boundary (2D) and precipitate (3D) (Jiang et al., 2025). Figure 24 shows the schematic views of those different phonon scattering sources in GeTe.
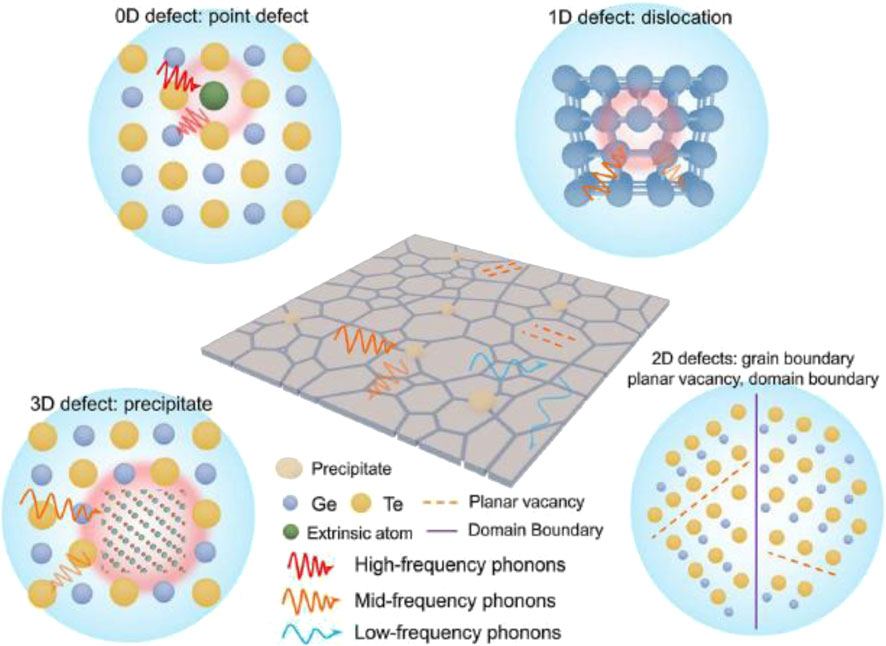
Figure 24. Schematic view for different types of phonon scattering sources in GeTe (Jiang et al., 2025).
A quite new physical paradigm for TE materials was recently proposed based on the superconducting Bardeen–Cooper–Schrieffer (BCS) theory and phonon drag effect (Liu and Cheng, 2025). According to the definition of the TE quality factor, high ZT values originate from material systems with high conductivity, large Seebeck coefficient, and low thermal conductivity. In the past few decades, traditional methods for optimizing TE performance have relied on electron-phonon transport separation, electronic band engineering, and phonon scattering mechanism modulation. However, even at various optimization levels, only moderate ZT values can be obtained. Therefore, another physical paradigm of synergistic electro/phonon transport based on the mechanism of electron-phonon interaction was proposed (Liu and Cheng, 2025). This approach is quite promising for improving ZT up to three or more.
Finally, several applications of AI and DL for modeling and predicting crystal structures are introduced. A study was reported, in which crystal structures were represented as graphs, where atoms are treated as nodes and interatomic bonds as edges (Xie and Grossman, 2018). Unlike traditional machine learning methods that rely on handcrafted features and are often limited to specific crystal types, Crystal Graph Convolutional Neural Networks (CGCNN) automatically learns representations from raw crystal structures. The model demonstrates high accuracy in predicting eight material properties derived from density functional theory (DFT), including band gap, formation energy, and elastic moduli. Importantly, CGCNN also provides interpretability by quantifying the contribution of local chemical environments to the overall property prediction, enabling insights into structure–property relationships and guiding materials design (Xie and Grossman, 2018).
Another study was reported, in which recent advances in predicting lattice thermal conductivity (κL) using machine learning (ML) techniques are reviewed (Luo et al., 2023). Traditional methods like first-principles calculations and molecular dynamics are accurate but computationally expensive. ML approaches offer a promising alternative by learning from existing data to predict κL efficiently. The review categorizes ML models into three types: descriptor-based models, graph-based models, and hybrid approaches. It also discusses the importance of data quality, feature engineering, and model interpretability. The authors highlight challenges such as data scarcity and generalizability and suggest future directions including active learning and integration with high-throughput screening. Figure 25 shows high-throughput prediction of lattice thermal conductivities by ML models (Luo et al., 2023).
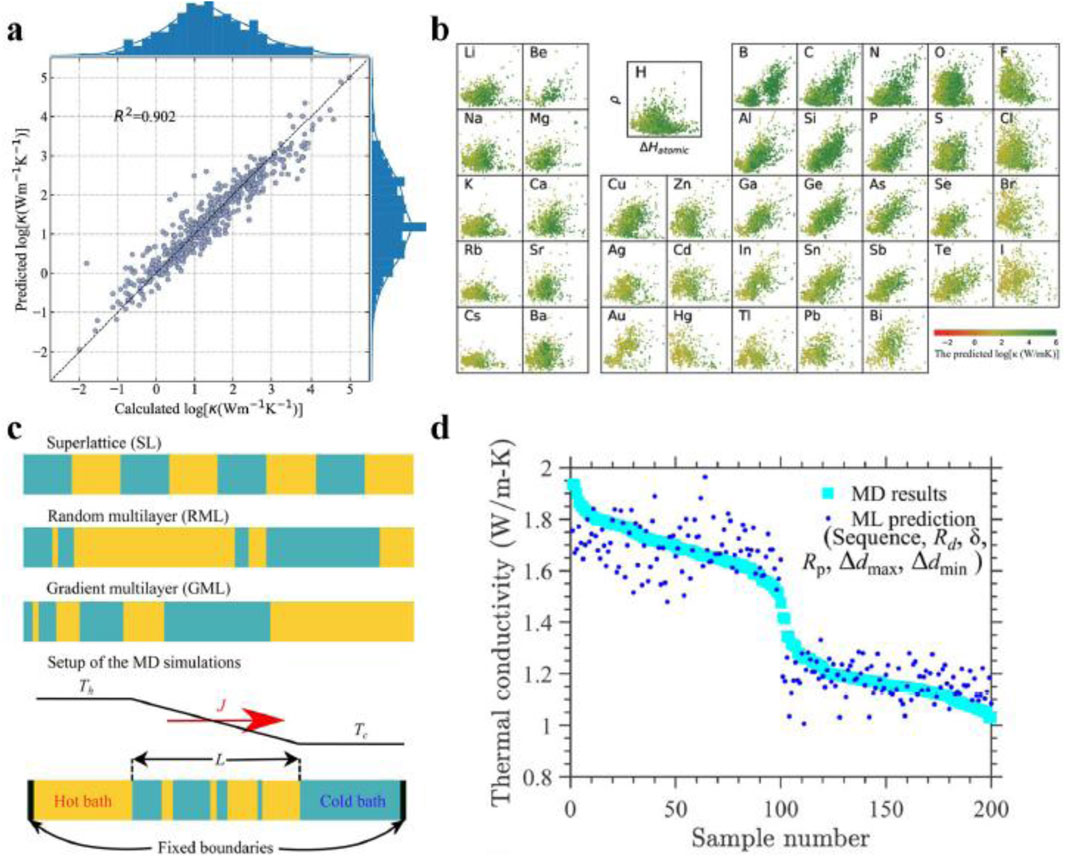
Figure 25. High-throughput prediction of lattice thermal conductivities by ML models (Luo et al., 2023). (a) The XGBoost model-predicted log scaled κL versus the calculated values for the testing set. The top and right histograms show the corresponding data distributions. (b) Dependence of the predicted κL on specific elements for compounds in the Inorganic Crystallographic Structure Database (ICSD), and the values are shown by colors along with the ΔHatomic and ρ. (c) Schematics of the multilayer structures and the MD simulation setup. (d) Comparisons of the real and predicted κL for 100 randomly generated RMLs and their corresponding 100 GMLs in the testing set (Luo et al., 2023).
5 Conclusion: summary and future prospects
This study has presented comprehensive review of the modeling and design of micro-structures in Functionally Graded Materials (FGMs), emphasizing their evolution from early aerospace applications to advanced energy conversion systems. FGMs, characterized by spatially varying phase compositions and micro-structures, offer unique advantages in tailoring material properties to meet specific performance requirements, particularly under extreme thermal and mechanical conditions. Micro-structural features such as phase distribution, grain size, shape, and porosity play a critical role in determining the behavior of FGMs. The design of FGMs is inherently an inverse problem, requiring precise control over these features during fabrication. Analytical and computational tools including Finite Element Method (FEM), multi-scale modeling, micro-mechanics, and fracture analysis have become essential for predicting and optimizing material performance. In energy conversion applications, particularly thermoelectric materials, FGMs have demonstrated significant potential in enhancing the figure of merit (ZT) through lattice and grain boundary engineering. Concepts such as quantum confinement, energy filtering, and phonon scattering have been successfully applied to improve thermal and electrical transport properties.
Recent advancements in artificial intelligence (AI) and deep learning (DL) have revolutionized micro-structure design. Generative models such as GANs, DDPMs, and VQ-VAEs enable high-fidelity inverse design, while Transformer-based architectures facilitate natural language-driven material generation. Tools like MCRpy and CGCNN further support property prediction and micro-structure reconstruction. Also, several applications of AI and DL for modeling and prediction of crystal structures and lattice thermal conductivity are introduced quite recently.
Additive Manufacturing (AM) technologies, including Direct Energy Deposition (DED) and Wire-Arc Additive Manufacturing (WAAM), have enabled the fabrication of complex FGMs with spatially controlled properties. AI-assisted monitoring and quality control are enhancing the reliability of these processes.
The integration of AI-driven design automation, advanced AM, and multi-physics optimization will be quite important in modeling and design of micro-structures for the next-generation FGMs. These materials are expected to play a transformative role across aerospace, energy, biomedical, and robotics sectors, offering multifunctional solutions with superior structural, thermal, and environmental compatibility.
Author contributions
TH: Writing – review and editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
Author TH was employed by Daikin Industries, Ltd.
Generative AI statement
The author(s) declare that Generative AI was used in the creation of this manuscript. The author(s) verify and take full responsibility for the use of generative AI in the preparation of this manuscript. Generative AI was used Search for relevant papers. Translate the documents.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alagha, A. N., Hussain, S., and Zaki, W. (2021). Additive manufacturing of shape memory alloys: a review with emphasis on powder bed systems. Mater. Des. 204, 109654. doi:10.1016/j.matdes.2021.109654
Alkunte, S., Fidan, I., Naikwadi, V., Gudavasov, S., Ali, M. A., Mahmudov, M., et al. (2024a). Advancements and challenges in additively manufactured functionally graded materials: a comprehensive review. J. Manuf. Mater. Process. 8 (1), 23. doi:10.3390/jmmp8010023
Alkunte, S., Gupta, M., Rajeshirke, M., More, N., Cheepu, M., Gupta, A., et al. (2024b). Functionally graded metamaterials: fabrication techniques, modeling, and applications—a review. Processes 12 (10), 2252. doi:10.3390/pr12102252
Alrfou, K., Zhao, T., and Kondijazi, A., A transfer learning for microstructure segmentation with CS-Net: a hybrid algorithm with transformer and CNN encoders. (2023). arXiv:2308.13917v1
Arai, Y., Kobayashi, H., and Tamura, M. (1993). Elastic-plastic thermal stress analysis for optimum material design of functionally gradient material. Trans. JSME 59 (559), 849–855. doi:10.1299/kikaia.59.849
Azqadan, E., Jahed, H., and Arami, A. (2023). Predictive microstructure image generation using denoising diffusion probabilistic models. Acta Mater. 261, 119406. doi:10.1016/j.actamat.2023.119406
Bendsoe, M. P., and Kikuchi, N. (1998). Generating optimal topologies in structural design using a homogenization method. Comp. Methods Appl. Mech. Eng. 71, 197–224. doi:10.1016/0045-7825(88)90086-2
Bohuder, S. K., Sharma, R., and Mishra, P. R. (2014). Functionally graded materials: a critical review. Int. J. Sci. Footprints 2 (4), 1 8–29.
Chen, G., Dresselhaus, M. S., Dresselhaus, G., Fleurial, J. P., and Caillat, T. (2003). Recent developments in thermoelectric materials. Int. Mater. Rev. 48, 45–66. doi:10.1179/095066003225010182
Dai, H., Zhang, X., Zheng, Y., Pei, W., Zhou, R., Liu, R., et al. (2022). Review and prospects of metamaterials used to control elastic waves and vibrations. Front. Phys. 10, 1069454. doi:10.3389/fphy.2022.1069454
Erdogan, F., and Wu, B. H. (1997). The surface crack problem for a plate with functionally graded properties. J. Appl. Mech. 64 (3), 449–456. doi:10.1115/1.2788914
Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 241 (No.1226), 376–396.
Fu, L., Yin, M., Wu, D., Li, W., Feng, D., Huang, L., et al. (2017). Large enhancement of thermo-electric properties in n-type PbTe via dual-site point defects. Energy Environ. Sci. 10, 2030–2040. doi:10.1039/c7ee01871a
Fu, N., Wei, L., Song, Y., Li, Q., Xin, R., Omee, S., et al. (2023). Material transformers: deep learning language models for generative materials design. Mach. Learn. Sci. Technol. 4, 015001. doi:10.1088/2632-2153/acadcd
Fukui, Y. (1991). Fundamental investigation of functionally gradient material manufacturing system using centrifugal force. JSME Int. J. Ser. III-Vibration Control Eng. 34 (1), 144–148. doi:10.1299/jsmec1988.34.144
Haghdadi, N., Laleh, M., Moyle, M., and Primig, S. (2021). Additive manufacturing of steels: a review of achievements and challenges. J. Mater Sci. 56, 64–107. doi:10.1007/s10853-020-05109-0
Hicks, L. D., and Dresselhaus, M. S. (1993). Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 47, 12727–12731. doi:10.1103/physrevb.47.12727
Hiraide, K., Hirayama, K., Endo, K., and Muramatsu, M. (2021). Application of deep learning to inverse design of phase separation structure in polymer alloy. Comput. Mater. Sci. 190 (1), 110278. doi:10.1016/j.commatsci.2021.110278
Hirano, T. (1995). From thermal stress relaxation type FGM to energy conversion type FGM. Osaka: JSME, pp126–pp131.
Hirano, T., Teraki, J., and Yamada, T. (1990). “On the design of functionally gradient materials,” in Proc. The first int. Symposium on FGM. Sendai.
Hirano, T., Teraki, J., and Yamada, T. (1991). “Applications of fuzzy theory to the design of functionally gradient materials,” in 11th int. conf. on structural mechanics in reactor technology. SD1-SD2, 49–54.
Hirano, T., Whitlow, L. W., Teraki, J., and Miyajima, M. (1994). Gradient potential design for functionally gradient energy conversion materials. Proc. 3rdInt. Symposium FGMs, 633.
Ho, J., Jain, A., and Abbeel, P. (2020). “Denoising diffusion probabilistic models,” in 34thConf. Neural Inf. Proc. Systems. NeurIPS. doi:10.48550/arXiv.2006.11239
Hu, H., Zhuang, H., Jiang, Y., Shi, J., Li, J., Cai, B., et al. (2021). Thermoelectric Cu12-Sb4S13-based synthetic minerals with a sublimation-derived porous network. Adv. Mater. 33, 2103633. doi:10.1002/adma.202103633
Jiang, Y., Yu, J., Li, H., Zhang, H. L., and Li, J. (2025). Chemical modulation and defect engineering in high-performance GeTe-based thermoelectrics. Chem. Sci. 16, 1617–1651. doi:10.1039/d4sc06615d
Jumper, J., Hassabis, D., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596 (26 August), 583–589. doi:10.1038/s41586-021-03819-2
Kawai, C., Teraki, J., Hirano, T., and Nomura, T. (1992). Fabrication of a functionally gradient material of TiC-SiC system by chemical vapor deposition. J. Ceram. Soc. Jpn. 100 (9), 1117–1121. doi:10.2109/jcersj.100.1117
Kondo, H., Yokoyama, A., Omori, M., Ohkubo, A., Hirai, T., Watari, F., et al. (2004). Fabrication of Titanium Nitride/Apatite functionally graded implants by spark plasma Sintering. Mater. Trans. 45 (No. 11), 3156–3162. doi:10.2320/matertrans.45.3156
Liu, H., and Cheng, X., Electron and phonon transport mechanisms in thermoelectric materials. (2025). doi:10.5772/intechopen.1010139
Luo, Y., Li, M., Yuan, H., Liu, H., and Fang, Y. (2023). Predicting lattice thermal conductivity via machine learning: a mini review. Npj Comput. Mater. 9, 4. doi:10.1038/s41524-023-00964-2
Moes, N., Dolbow, J., and Belytschko, T. (1999). A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46 (Issue 1), 131–150. doi:10.1002/(sici)1097-0207(19990910)46:1<131::aid-nme726>3.0.co;2-j
Narducci, D., Selezneva, E., Cerofolini, G., Frabboni, S., and Ottaviani, G. (2012). Impact of energy filtering and carrier localization on the thermoelectric properties of granular semiconductors. J. Solid State Chem. 193, 19–25. doi:10.1016/j.jssc.2012.03.032
Neophytou, N., Vargiamidis, V., Foster, S., Graziosi, P., de Sousa Oliveira, L., Chakraborty, D., et al. (2020). Hierarchically nanostructured thermoelectric materials: challenges and opportunities for improved power factors. Eur. Phys. J. B 93, 213. doi:10.1140/epjb/e2020-10455-0
Niino, M., Hirai, T., and Watanabe, R. (1987). The functionally gradient materials -Aiming for ultra-heat-resistant materials for spacecraft. J. Jpn. Soc. Compos. Mater. 13, 257–264. doi:10.6089/jscm.13.257
Niino, M., Suzuki, A., Hirai, J., Watanabe, R., Hirano, T., and Kuroishi, N. (1988a). Method of producing a functionally gradient material. USP4751099. June, 14.
Niino, M., Yatsuyanagi, N. I. J., Hirano, T., and Sumiyoshi, K. (1988b). Method of producing composite materials. USP4778649. October, 18.
Nishio, Y., and Hirano, T. (1997). Improvement of the efficiency of thermoelectric energy conversion by utilizing potential barriers. Jpn. J. Appl. Phys. 36 (Pt.1), 1A.
Noguchi, S., and Inoue, J. (2024). Bayesian inverse inference of material properties from microstructure images. Comput. Mater. Sci. 245, 113306. doi:10.1016/j.commatsci.2024.113306
Noguchi, S., Wang, H., and Inoue, J. (2022). Identification of microstructures critically affecting material properties using machine learning framework based on metallurgists’ thinking process. Sci. Rep. 12, 14238. doi:10.1038/s41598-022-17614-0
Noronha, J., Dash, J., Leary, M., Warson, M., Qian, M., Kyriakou, E., et al. (2023). Additively manufactured functionally graded lattices: design, mechanical response, deformation behavior, applications, and insights. JOM 75 (12), 5729–5754. doi:10.1007/s11837-023-06190-x
Nowler, M. A. A., Abd-Elhady, A. A., Sallam, H., El-Din, M., and Atta, M. (2025). Enhancing the tribological performance of polymeric laminated composite materials by adopting the functionally graded materials technique. Archives Civ. Mech. Eng. 25, 167. doi:10.1007/s43452-025-01224-4
Pan, Y., Wei, T. R., Wu, F. C., and Li, J. F. (2015). Electrical and thermal transport properties of spark plasma sintered n-type Bi2Te3-xSex alloys: the combined effect of point defect and Se content. J. Mater. Chem. C August 3, 10583–10589. doi:10.1039/C5TC02219C
Peng, X.-L., Fathidoost, M., Lin, B., Yang, Y., and Xu, B.-X. (2025). What can machine learning help with microstructure-informed materials modeling and design? MRS Bull. 50 (January), 61–79. doi:10.1557/s43577-024-00797-4
Petrova, V., and Schmauder, S. (2021). Thermal fracture of functionally graded thermal barrier coatings with pre-existing edge cracks and multiple internal cracks imitating a curved interface. Contin. Mech. Thermodyn. 33, 1487–1503. doi:10.1007/s00161-021-00994-5
Reddy, J. N. (2000). Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 47, 663–684. doi:10.1002/(sici)1097-0207(20000110/30)47:1/3<663::aid-nme787>3.0.co;2-8
Rhee, R. S. (2007). Multi-scale modeling of functionally graded materials (FGMs) using finite element methods. December: Dissertation to University of Southern California.
Sabarinathan, M., Omprakash, M., Harish, S., Navaneethan, M., Archana, J., Ponnusamy, S., et al. (2016). Enhancement of power factor by energy filtering effect in hierarchical BiSbTe3 nanostructures for thermoelectric applications. Appl. Surf. Sci. Dec. 418, 246–251. doi:10.1016/j.apsusc.2016.12.010
Sanjeeviprakash, K., Kannan, A. R., and Shanmugam, N. S. (2023). Additive manufacturing of metal-based functionally graded materials: overview, recent advancements and challenges. J. Braz. Soc. Mech. Sci. Eng. 45, 241. doi:10.1007/s40430-023-04174-1
Sasaki, M., Wang, Y., Hirano, T., and Hirai, T. (1989). Design of SiC/C functionally gradient material and its Preparation by chemical vapor deposition. J. Ceram. Soc. Jpn. 97 (5), 539–543. doi:10.2109/jcersj.97.539
Sata, N. (1993). Characteristic of SiC–TiB2 composites as the surface layer of SiC–TiB2–Cu functionally gradient material produced by self-propagating high-temperature synthesis. Ceram. Trans. Funct. Gradient Mater. 34, 109–116.
Seibert, P., Rassloff, A., Kalina, K., Ambati, M., and Kastner, M. (2022). Microstructure characterization and reconstruction in Python. MCRpy. Integrating Mater. Manuf. Innovation 11, 450. doi:10.1007/s40192-022-00273-4
Shahzamanian, M. M., Patovi, A., and Wu, P. D. (2020). Finite element analysis of elastic-plastic and fracture behavior in functionally graded materials (FGMs). SN Appl. Sci. 2, 2135. doi:10.1007/s42452-020-03901-w
Silva, R. F., Coelho, P. G., Gustavo, C. V., Almeida, C. J., Farias, F. W. C., Duarte, V. R., et al. (2024). Functionally graded materials and structures: unified approach by optimal design, metal additive manufacturing, and image-based characterization. Materials 17 (18), 4545. doi:10.3390/ma17184545
Sinha, A. K., and Pamnani, G. (2025). Applications of XFEM in fracture analysis: a review. Int. J. Sci. Technol. Trans. Civ. Eng., 18 July. doi:10.1007/s40996-025-01955-7
Smith, D. R., Schurig, D., Starr, A. F., and Mock, J. J., METAMATERIALS. USP7538946 B2, may 26 (2009).
Suresh, S., and Mortensen, A. (1998). Fundamentals of functionally graded materials: processing and thermomechanical behavior of graded metals and metal-ceramic composites. London: IOM Communications Ltd.
Tan, R. K., Zhang, N. L., and Ye, W. (2020). A deep learning–based method for the design of microstructural materials. Struct. Multidisc Optim. 61, 1417–1438. doi:10.1007/s00158-019-02424-2
Teraki, J., Hirano, T., and Wakashima, K. (1992). An elastic-plastic analysis of thermal stresses in a FGM plate under Cyclic thermal load. Proc. 2nd Int. Symposium FGM.
Tukamoto, H. (2017). Structural analysis and characterization of functionally graded materials. J. Jpn. Soc. Precis. Eng. 83 (No.5), 405–410. doi:10.2493/jjspe.83.405
Urban, J. J., Menon, A. K., Tian, Z., Jain, A., and Hippalgaonkar, K. (2019). New horizons in thermoelectric materials: correlated electrons, organic transport, machine learning, and more. J. Appl. Phys. 125, 180902. doi:10.1063/1.5092525
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention is all You need,” in 31stconf. Neural Inf. Proc. Systems. NeurIPS.
Veselago, V. G. (1967). The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Uspekhi 10 (4), 509–514. doi:10.1070/pu1968v010n04abeh003699
Wasmer, K., Wust, M., Cui, D., Masinelli, G., Pandiyan, V., and Shevchik, S. (2023). Monitoring of functionally graded material during laser directed energy deposition by acoustic emission and optical emission spectroscopy using artificial intelligence. Virtual Phys. Prototype. 18, e2189599. doi:10.1080/17452759.2023.2189599
Whitlow, L. W., and Hirano, T. (1995). Superlattice applications to thermoelectricity. J. Appl. Phys. 78 (No.9), 5460–5466. doi:10.1063/1.359661
Xie, T., and Grossman, J. C. (2018). Crystal graph Convolutional neural networks for an accurate and interpretable prediction of material properties. arXiv:1710.10324v3.
Xu, C., Wang, Y., and Farimani, A. B. (2023). TransPolymer: a Transformer-based language model for polymer property predictions. Npj Comput. Mater. 9, 64. doi:10.1038/s41524-023-01016-5
Yang, Z., and Buehler, M. (2021). Words to Matter: de novo architected materials design using transformer neural networks. Front. Mater. 8, 740754 October. doi:10.3389/fmats.2021.740754
Zhang, L., Wang, B., Song, B., Yao, Y., Chol, S.-K., Yang, C., et al. (2023). 3D printed biomimetic metamaterials with graded porosity and tapering topology for improved Cell Seeding and bone Regeneration. Bioact. Mater. 25, 677–688. doi:10.1016/j.bioactmat.2022.07.009
Keywords: computational materials science, modeling and design of micro-structures, constitutive material modeling, FGMs (functionally graded materials), multi-scale modeling, deep learning, material transformer, additive manufacturing
Citation: Hirano T (2025) Modeling and design of micro-structures: focusing on functionally graded materials and future prospects. Front. Mater. 12:1659727. doi: 10.3389/fmats.2025.1659727
Received: 04 July 2025; Accepted: 15 August 2025;
Published: 22 October 2025.
Edited by:
Mayu Muramatsu, Keio University, JapanReviewed by:
Agnivesh Kumar Sinha, Rungta College of Engineering and Technology, IndiaCopyright © 2025 Hirano. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tohru Hirano, dG9ocnUuaGlyYW5vQGRhaWtpbi5jby5qcA==
 Tohru Hirano
Tohru Hirano