Analysis of expected value of connectivity indices of random 2T2 kink chains

In this work, we calculated the product connectivity index of three structures for the $T_2$-type twists and formulated expressions of expected values of the forgotten index, atom bond connectivity index, sum connectivity index, product connectivity index and geometric arithmetic index of these random structures in the $(\acute{\eta }-2)$ stage. In addition, we calculated the expected values numerically, graphically and analytically and found the topological indices that have the maximum and minimum value.

1 Introduction

A square-hexagonal system is connected geometric shape and a unique geometric arrangement formed by connecting equal sized squares and/or hexagons together. In this system, the lattice points form a repeating pattern that resembles a combination of squares and hexagons. In contrast, a square-hexagonal chain is a one-dimensional linear sequence where square and hexagonal units alternate or connect in a line, creating a chain-like arrangement. This configuration is useful in fields like combinatorics and polymer chemistry, where alternating shapes along a single axis influence the overall behavior and properties of the chain. Different square-hexagoal chains are formed depending on the way how polygons are concatenated.

A [1, 2] polyomino chain is a sequence of connected squares, where each square shares at least one side with the next in the sequence. A hexagonal chain is a one-dimensional, linear sequence of connected hexagonal units, where each hexagon is linked to the next in a chain-like formation. Unlike a full hexagonal lattice, which extends in two dimensions, a hexagonal chain progresses in a single direction, creating a structure that resembles a series of hexagonal “tiles” arranged side by side. In graph theory, a graph $\psi$ is defined as an ordered pair $\psi =(V_{\psi },E_{\psi })$, where $V_{\psi }$ (also called vertices or nodes) is a set elements that represent pints in a graph and $E_{\psi }$ (called edges or arcs) is a set of pairs of vertices. Each pair $(u,v)$ represents a connection (edge) between two vertices $u$ and $v$.

Topological indices are the quantitative values that represent the structural characteristic of a graph which are used to relate the structure with its physical and chemical properties. These indices are usually known as descriptors of graphical structures for precisely this reason. These are the conclusions reached by applying logic and mathematics to a symbolic representation of a graph in an usable number. Some topological descriptors which we have used in our paper are described below.

The [3] geometric-arithmetic index is defined as;

$GA\left(\psi \right)={\displaystyle \sum _{uv\in E\left(\psi \right)}}\frac{2\sqrt{d_u\times d_v}}{d_u+d_v}(1)$

The sum-connectivity and product-connectivity indices are defined respectively as;

$SC\left(\psi \right)={\displaystyle \sum _{uv\in E\left(\psi \right)}}\frac{1}{\sqrt{d_u+d_v}}(2)$

$PC\left(\psi \right)={\displaystyle \sum _{uv\in E\left(\psi \right)}}\frac{1}{\sqrt{d_u\times d_v}}(3)$

Different relations between these two indices are established in [4].

In article [5] the forgotten index is given as;

$F\left(\psi \right)={\displaystyle \sum _{uv\in E\left(\psi \right)}}{\left(d_u\right)}^3$

or it can also be defined as;

$F\left(\psi \right)={\displaystyle \sum _{uv\in E\left(\psi \right)}}\left[{\left(d_u\right)}^2+{\left(d_v\right)}^2\right](4)$

The [6] atom bond connectivity index is defined as;

$ABC\left(\psi \right)={\displaystyle \sum _{uv\in E\left(\psi \right)}}\sqrt{\frac{d_u+d_v-2}{d_u\times d_v}}(5)$

In mathematical chemistry the application of chemical graph theory to the study of complex structures, using different chemical invariants, has revolutionary effects. The total count of nodes or vertices in a graph is known as its order, represented by $|V_{\psi }|$. Whereas the total count of edges between the nodes in a graph is called its size which is represented by $|E_{\psi }|$. In a molecular graph atoms are represented by $u\in V_{\psi }$, while $u_i{v}_j\in E(\psi )$ represents the bonds connecting the corresponding atoms. The degree of a vertex, indicated by $deg(u)$ or $d_u$, refers to the count of edges connected to that vertex. Further notations of graph are discussed in [7].

Phenylene chains are part of a broader class of conjugated organic polymers, formed by joining squares and hexagons alternatively. Raza et al. in [8] compared numerically as well as graphically, the random phenylene chains among the expected values of atom bond connectivity and geometric-arithmetic indices. Wei et al. [9] formulated the expected values of various topological indices for random phenylene chains using auxiliary graphical structures, with a particular focus on the Merrifield-Simmons index.

Several researchers [10–12] have provided exact expressions and comparative analyses of topological indices for chemical graph structures, including random phenylene and polyphenyl chains. In [2], Sigarreta et al. computed the Sombor, Forgotten, Zagreb, Atom-Bond Connectivity, Randic, and Geometric-Arithmetic indices for polyomino chains, deriving precise expressions for their expected values and variances in random polyomino structures.

The first Zagreb connection index, a widely studied topological descriptor, has been extensively used to investigate the structural properties and chemical stability of molecular networks. Recent studies [14] have explored its expected value in random cyclooctatetraene chains, random polyphenyl chains, and random chain networks, providing valuable insights into the probabilistic behavior of these indices in complex molecular structures. This research contributes significantly to the understanding of topological indices in stochastic chemical graph theory, particularly in the context of polymers and organic chain networks. Distance-based graphical indices have proven highly effective in predicting the thermodynamic properties of benzenoid hydrocarbons [15], highlighting their practical applications in computational chemistry and materials science.

Similarly, eigenvalue-based graphical indices have demonstrated significant predictive capabilities in modeling and determining the thermodynamic properties of polycyclic aromatic hydrocarbons [16]. This method has been particularly useful in studying polyacenes, providing valuable insights into their structural and thermal behavior.

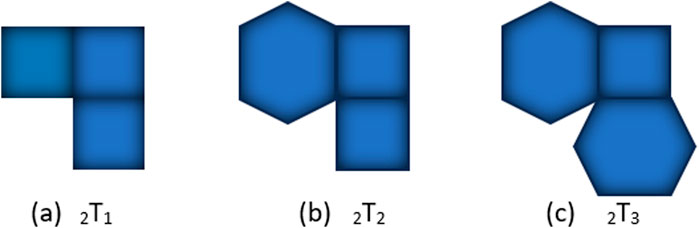
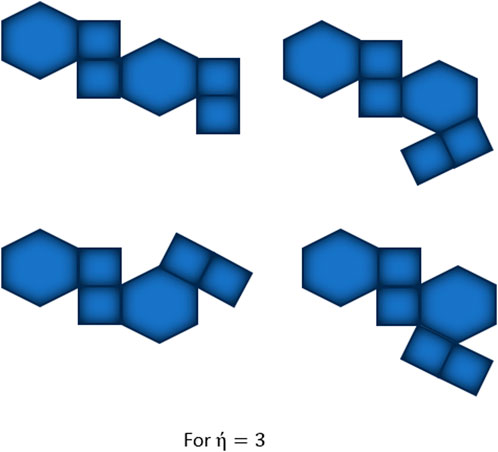
Furthermore, temperature-based topological indices have been utilized in structure-property modeling to predict the thermodynamic properties of benzenoid hydrocarbons [17], contributing to a deeper understanding of their thermal characteristics. Depending on the attachment of polygons and graphical representation, there are two types of square-hexagonal kinks, kinks of type $T_1$ and $T_2$. In type $T_1$ hexagon occurs as a kink holding the criteria to have two adjacent vertices of degree two. While in type $T_2$, a square is said to be a kink if contains a vertex of degree 2. Kinks of type $T_2$ are divided into three types [1] based on the possibilities of connecting polygons (square and hexagon) at different places of a square. These three types, ${}_{2}T_1,{}_{2}T_2$ and ${}_{2}T_3$, are shown in Figure 1

Figure 1

Figure 1. Kinks of type ${}_{2}T_1,{}_{2}T_2$ and ${}_{2}T_3$.

By considering $\acute{\eta }$ being the kink, we have further discovered three types of kink chains of type ${}_{2}T_2$, named as [18] ${}_{2}T_2^1$, ${}_{2}T_2^2$ and ${}_{2}T_2^3$. Also computed Forgotten, atom-bond connectivity, Sum-connectivity and Product-connectivity indices of these chains and found out the maximizing and minimizing index using graphical representation. For the sake of generality, we expressed our results into odd and even numbered kink chains. In graph theory, the concept of expected value is not inherently a property of a graph, but it is often used in the context of random graphs or randomized processes on graphs.

In [19], we calculated $1^{st}$ and $2^{nd}$ Gourava, $1^{st}$ and $2^{nd}$ Revan, Redefind $1^{st}$ and $2^{nd}$ Zagreb and Hyper-Zagreb indices of these three structures of kink chains of type ${}_{2}T_2$ and found out maximizing and minimizing index. In addition to that, we also got the expected valued values for these descriptors at ${(\acute{\eta }-1)}^{th}$ stage and made comparison among them.

We are motivated to consider square and hexagonal kink chains in our work due to their superior mechanical and structural properties, which are highly relevant in material science and engineering applications due to their unique geometric and mechanical properties. They enhance stress distribution and energy absorption, making them ideal for impact-resistant materials in aerospace, automotive, and structural engineering. A comprehensive examination of these structural and topological characteristics offers valuable understanding of how kink chains impact material properties, forming a crucial foundation for bridging theoretical outcomes with practical engineering applications. This research establishes a basis for future studies to implement these insights in addressing specific engineering challenges, including the design and optimization of materials for advanced technological applications.

2 Methodology

In this study, we employed a comprehensive methodology to analyze the connectivity indices of random $T_2$ kink chains. We began by graphically representing the kink structures as graphs, where vertices denote atoms and edges represent bonds. We calculated several topological indices including the Product Connectivity Index $(PC)$, Sum Connectivity Index $(SC)$, Atom Bond Connectivity Index $(ABC)$, and Forgotten Index $(F)$ using established mathematical definitions. The expected values of these indices were derived at various stages of the kink evolution, employing relationships from previous literature in mathematical chemistry. Numerical analysis were performed to identify the maximizing and minimizing values of these indices, complemented by graphical visualizations to portray their behavior throughout the kinking process. Finally, a comparative analysis with existing studies allowed us to validate our results and deepen our understanding of the structural implications of these connectivity indices in molecular networks.

3 Main results

In this article, we will expand our work and calculate $PC$ index of three possible arrangements of kinks of type ${}_{2}T_2$ and the expected value of $PC$, $SC$, $F$, $ABC$ and $GA$ indices of three random structures for the kink of type ${}_{2}T_2$. We will numerically, graphically as well as analytically find out the maximizing and minimizing expectation at ${(\acute{\eta }-2)}^{th}$ stage.

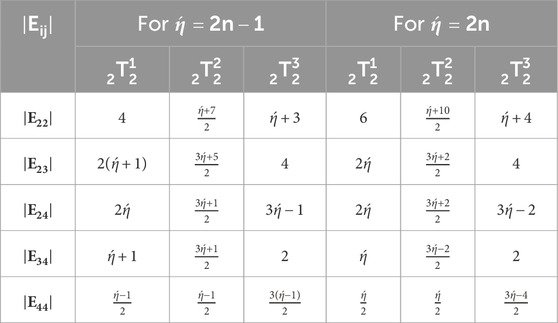
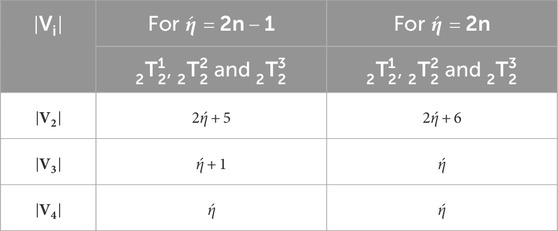
Let $\acute{\eta }$ represents the kink. Tables 1, 2 represents the vertex and edge partitions of each kink chain accordingly [18].

Table 1

Table 1. Edge partitions of ${}_{2}T_2^1$, ${}_{2}T_2^2$ and ${}_{2}T_2^3$; $n\in N$.

Table 2

Table 2. Vertex partitions of ${}_{2}T^1$, ${}_{2}T_2^2$ and ${}_{2}T_2^3$.

Theorem 3.1. Let $n\in N$, then the product connectivity topological index of kink chain $T_{\mathrm{2,2}}^p$ is given as;

$PC\left(T_{\mathrm{2,2}}^p\right)=\left\{\begin{array}{cc}1.937278497\acute{\eta }+2.980171716\hfill & \text{if}p=1\hfill \\ 1.950715223\acute{\eta }+2.966734989\hfill & \text{if}p=2;for\acute{\eta }=2n-1\hfill \\ 1.935660172\acute{\eta }+2.98179004\hfill & \text{if}p=3\hfill \end{array}\right.$

$PC\left(T_{\mathrm{2,2}}^p\right)=\left\{\begin{array}{cc}1.937278497\acute{\eta }+3\hfill & \text{if}p=1\hfill \\ 1.950715223\acute{\eta }+2.973126546\hfill & \text{if}p=2;for\acute{\eta }=2n\hfill \\ 1.935660172\acute{\eta }+3.00323665\hfill & \text{if}p=3\hfill \end{array}\right.$

Proof. Let $\acute{\eta }=2n-1$. Using the edge partition given in Table 1 and the definition of product connectivity topological index, we get

$\begin{array}{ll}\hfill PC\left(T_{\mathrm{2,2}}^1\right)& =\left(4\right)\left(\frac{1}{2}\right)+\left(2\left(\acute{\eta }+1\right)\right)\left(\frac{1}{\sqrt{6}}\right)+\left(2\acute{\eta }\right)\left(\frac{1}{2\sqrt{2}}\right)\hfill \\ \hfill & +\left(\acute{\eta }+1\right)\left(\frac{1}{2\sqrt{3}}\right)+\left(\frac{\acute{\eta }-1}{2}\right)\left(\frac{1}{4}\right)\hfill \\ \hfill & =1.937278497\acute{\eta }+2.980171716\hfill \end{array}$

$\begin{array}{cc}\hfill PC\left(T_{\mathrm{2,2}}^2\right)& =\left(\frac{\acute{\eta }+7}{2}\right)\left(\frac{1}{2}\right)+\left(\frac{3\acute{\eta }+5}{2}\right)\left(\frac{1}{\sqrt{6}}\right)+\left(\frac{3\acute{\eta }+1}{2}\right)\left(\frac{1}{2\sqrt{2}}\right)\hfill \\ \hfill & +\left(\frac{3\acute{\eta }+1}{2}\right)\left(\frac{1}{2\sqrt{3}}\right)+\left(\frac{\acute{\eta }-1}{2}\right)\left(\frac{1}{4}\right)\hfill \\ \hfill & =1.950715223\acute{\eta }+2.966734989\hfill \end{array}$

$\begin{array}{cc}\hfill PC\left(T_{\mathrm{2,2}}^3\right)& =\left(\acute{\eta }+3\right)\left(\frac{1}{2}\right)+\left(4\right)\left(\frac{1}{\sqrt{6}}\right)+\left(3\acute{\eta }-1\right)\left(\frac{1}{2\sqrt{2}}\right)\hfill \\ \hfill & +\left(2\right)\left(\frac{1}{2\sqrt{3}}\right)+\left(\frac{3\left(\acute{\eta }-1\right)}{2}\right)\left(\frac{1}{4}\right)\hfill \\ \hfill & =1.935660172\acute{\eta }+2.98179004\hfill \end{array}$

Let $\acute{\eta }=2n$. Using the edge partition given in Table 1 and the definition of product connectivity topological index, we get

$\begin{array}{cc}\hfill PC\left(T_{\mathrm{2,2}}^1\right)& =\left(6\right)\left(\frac{1}{2}\right)+\left(2\acute{\eta }\right)\left(\frac{1}{\sqrt{6}}\right)+\left(2\acute{\eta }\right)\left(\frac{1}{2\sqrt{2}}\right)+\left(\acute{\eta }\right)\left(\frac{1}{2\sqrt{3}}\right)+\left(\frac{\acute{\eta }}{2}\right)\left(\frac{1}{4}\right)\hfill \\ \hfill & =1.937278497\acute{\eta }+3\hfill \end{array}$

$\begin{array}{cc}\hfill PC\left(T_{\mathrm{2,2}}^2\right)& =\left(\frac{\acute{\eta }+10}{2}\right)\left(\frac{1}{2}\right)+\left(\frac{3\acute{\eta }+2}{2}\right)\left(\frac{1}{\sqrt{6}}\right)+\left(\frac{3\acute{\eta }+2}{2}\right)\left(\frac{1}{2\sqrt{2}}\right)\hfill \\ \hfill & +\left(\frac{3\acute{\eta }-2}{2}\right)\left(\frac{1}{2\sqrt{3}}\right)+\left(\frac{\acute{\eta }}{2}\right)\left(\frac{1}{4}\right)\hfill \\ \hfill & =1.950715223\acute{\eta }+2.973126546\hfill \end{array}$

$\begin{array}{cc}\hfill PC\left(T_{\mathrm{2,2}}^3\right)& =\left(\acute{\eta }+4\right)\left(\frac{1}{2}\right)+\left(4\right)\left(\frac{1}{\sqrt{6}}\right)+\left(3\acute{\eta }-2\right)\left(\frac{1}{2\sqrt{2}}\right)\hfill \\ \hfill & +\left(2\right)\left(\frac{1}{2\sqrt{3}}\right)+\left(\frac{3\acute{\eta }-4}{2}\right)\left(\frac{1}{4}\right)\hfill \\ \hfill & =1.935660172\acute{\eta }+3.00323665\hfill \end{array}$

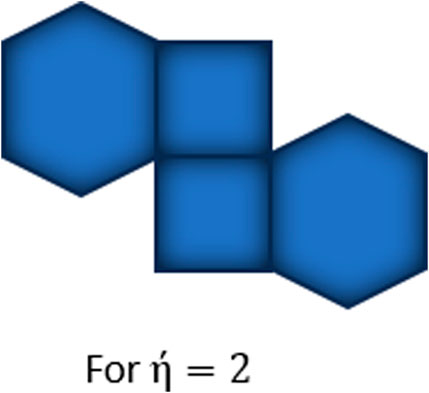
Observe that there is no edge between two adjacent vertices of degree 2, only one edge between two adjacent vertices of degree 2, and two edges between two adjacent vertices of degree two in three random (the second and third arrangements are same) structures of kink of type ${}_{2}T_2$ respectively, except at terminal polygons, so we have only three possible arrangements of type ${}_{2}T_2$, holding the conditions to make kink at each step. The possible arrangement for $\acute{\eta }=1$ is same as shown in Figure 1b and for $\acute{\eta }=2$ is shown in Figure 2. For $\acute{\eta }\ge 2$, the possible arrangements for attaching terminal polygons are shown in Figure 3 in three different ways, resulting three types [18]${}_{2}T_2^1$, ${}_{2}T_2^2$ and ${}_{2}T_2^3$. Let $\acute{\stackrel{́}{\gamma }}$ be the probability of attaching terminal polygons in the first or second kind of arrangement, then $1-2\acute{\stackrel{́}{\gamma }}$ be the probability of attaching the terminal polygon in the third type of arrangement.

Figure 2

Figure 2. Kinks of type ${}_{2}T_1,{}_{2}T_2$and ${}_{2}T_3$.

Figure 3

Figure 3. Possible arrangements of kink chains of type ${}_2\top _2$.

Consider kink chain ${}_{2}T_2$ with $\acute{\eta }$ number of kinks and probability $\acute{\stackrel{́}{\gamma }}$ is represented by ${({}_{\mathbf{2}}\mathbf{T}_{\mathbf{2}}^{\acute{\stackrel{́}{\mathit{\gamma }}}})}_{\acute{\stackrel{́}{\mathit{\eta }}}}$. Now we compute expected values of product-connectivity, Forgotten, atom-bond connectivity, product-connectivity and sum-connectivity indices of possible square-hexagonal kink chains ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$. Let $|E_{ij}|={\beta }_{ij}$ denotes the number of edges for ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ with end vertices of degree i and j accordingly. There are only ${\beta }_{22}$, ${\beta }_{23}$, ${\beta }_{24}$, ${\beta }_{34}$ and ${\beta }_{44}$-type of edges in ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$. From Equations 1–5, topological descriptors can be expressed as

$F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}=8{\beta }_{22}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+13{\beta }_{23}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+20{\beta }_{24}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+25{\beta }_{34}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+32{\beta }_{44}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}(6)$

$GA{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}={\beta }_{22}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+2\frac{\sqrt{6}}{5}{\beta }_{23}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+2\frac{\sqrt{2}}{3}{\beta }_{24}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+4\frac{\sqrt{3}}{7}{\beta }_{34}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+{\beta }_{44}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}(7)$

$SC{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}=\frac{1}{2}{\beta }_{22}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{\sqrt{5}}{\beta }_{23}\left({\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{\sqrt{6}}{\beta }_{24}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{\sqrt{7}}{\beta }_{34}\left({\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{2\sqrt{2}}{\beta }_{44}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}\right.\right.(8)$

$ABC{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}=\frac{\sqrt{2}}{4}{\beta }_{22}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{\sqrt{3}}{6}{\beta }_{23}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{4}{\beta }_{24}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{\sqrt{5}}{12}{\beta }_{34}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{\sqrt{6}}{16}{\beta }_{44}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}(9)$

$PC{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}=\frac{1}{2}{\beta }_{22}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{\sqrt{6}}{\beta }_{23}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{2\sqrt{2}}{\beta }_{24}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{2\sqrt{3}}{\beta }_{34}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}+\frac{1}{4}{\beta }_{44}{\left({}_{2}T_2^{\gamma }\right)}_{\acute{\eta }}(10)$

As ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ is a possible kink chain, it proceeds that $F{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$, $GA{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$, $SC{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$, $ABC{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ and $PC{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ are possible variables. Let us denote by $E_{\acute{\eta }}^F=E[F{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}]$, $E_{\acute{\eta }}^{GA}=E[GA{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}]$, $E_{\acute{\eta }}^{\mathit{ABC}}=E[ABC{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}]$, $E_{\acute{\eta }}^{SC}=E[SC{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}]$ and $E_{\acute{\eta }}^{PC}=E[PC{({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}]$ the expected values of these indices respectively.

To compute the expected values for above mentioned indices we will compute the change in edge partitions of ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ for three possible constructions of kink chains as shown in Figure 3. It is to be noted that if $\acute{\eta }$ is odd in possible arrangements (${}_{2}T_2^1$, ${}_{2}T_2^2$ and ${}_{2}T_2^3$) of kink chain then at ${(\acute{\eta }-1)}^{th}$ step, even numbered kink chains are formed and at ${(\acute{\eta }-2)}^{th}$ step, odd numbered kink chains are formed. Similarly, if $\acute{\eta }$ is even in possible arrangements of kink chain then at ${(\acute{\eta }-1)}^{th}$ step, odd numbered kink chains are obtained and at ${(\acute{\eta }-2)}^{th}$ step, even numbered kink chains are obtained again. We will formulate our expressions at ${(\acute{\eta }-2)}^{th}$ stage.

4 Results at ${(\acute{\eta }-2)}^{th}$ stage

The three possible constructions at ${(\acute{\eta }-2)}^{th}$ stage are as follows:

$\mathit{1}.{({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{1}})}_{\acute{\mathit{\eta }}}$

$\mathit{2}.{({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{2}})}_{\acute{\mathit{\eta }}}$

$\mathit{3}.{({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{3}})}_{\acute{\mathit{\eta }}}$

It is interested to note that change in edge partitions of ${({}_{2}T_2^{\acute{\gamma }})}_k$ remains same for $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$ when we take ${(\acute{\eta }-2)}^{th}$ stage. Change in edge partitions of ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ at ${(\acute{\eta }-2)}^{th}$ stage for $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$ is shown in Table 3

Table 3

Table 3. Change in edge partitions of ${({}_{2}T_2^{\acute{\gamma }})}_k$ at ${(\acute{\eta }-2)}^{th}$ step for $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$; $n\in n$.

Theorem 4.1. For square-hexagonal kink chain ${}_{2}T_2$ with $\acute{\eta }$ number of kinks, we have

(a) For $\acute{\eta }=2n-1$; $n\in N$

$E_{\acute{\eta }}^F=\acute{\eta }\left[-18\acute{\gamma }+116\right]+18\acute{\gamma }+58$

(b) For $\acute{\eta }=2n$; $n\in N$

$E_{\acute{\eta }}^F=\acute{\eta }\left[-18\acute{\gamma }+116\right]+36\acute{\gamma }+30$

Proof. Let $\acute{\eta }\ge 2$, then there are three possibilities. Using Table 3 and Equation 3, we get

$\mathit{1}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{1}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill F{\left({}_{2}T_2^1\right)}_{\acute{\eta }}& =8{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+13\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]+20\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]\hfill \\ \hfill & +25\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+32\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \end{array}$

$=F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+214(11)$

$\mathit{2}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{2}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill F{\left({}_{2}T_2^2\right)}_{\acute{\eta }}& =8\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]+13\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+20\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]\hfill \\ \hfill & +25\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+32\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \end{array}$

$=F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+214(12)$

$\mathit{3}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{3}})}_{\acute{\mathit{\eta }}}$, then

$F{\left({}_{2}T_2^3\right)}_{\acute{\eta }}=8\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+13{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+20\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+6\right]+25{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+32\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]=F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+232(13)$

Thus, we have

$E_{\acute{\eta }}^F=\acute{\gamma }F{\left({}_{2}T_2^1\right)}_{\acute{\eta }}+\acute{\gamma }F{\left({}_{2}T_2^2\right)}_{\acute{\eta }}+\left(1-2\acute{\gamma }\right)F{\left({}_{2}T_2^3\right)}_{\acute{\eta }}$

Using Equations 11–13, we get the following relation

$E_{\acute{\eta }}^F=\acute{\gamma }\left[F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+214\right]+\acute{\gamma }\left[F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+214\right]+\left(1-2\acute{\gamma }\right)\left[F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+232\right]=F{\left({}_{2}T_2\right)}_{\acute{\eta }-2}-36\acute{\gamma }+232$

Applying operator E on both sides and $\therefore E(E_{\acute{\eta }}^F)=E_{\acute{\eta }}^F$

$E_{\acute{\eta }}^F=E_{\acute{\eta }-2}^F-36\acute{\gamma }+232$

$•$ Let $\acute{\eta }=2n-1$

For $n=1\Rightarrow \acute{\eta }=1$, $E_1=174$, which is indeed true. Using recursive relation upto $\acute{\eta }-1$ trerms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^F& =E_{\acute{\eta }-\left(\acute{\eta }-1\right)}^F+\left(\frac{\acute{\eta }-1}{2}\right)\left[-36\acute{\gamma }+232\right]=174+\left(\acute{\eta }-1\right)\left[-18\acute{\gamma }+116\right]\hfill \\ \hfill & =\acute{\eta }\left[-18\acute{\gamma }+116\right]+18\acute{\gamma }+58\hfill \end{array}$

which completes the result.

$•$ Let $\acute{\eta }=2n$

For $n=1\Rightarrow \acute{\eta }=2$, $E_2=262$, which is indeed true. Using recursive relation upto $\acute{\eta }-2$ terms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^F& =E_{\acute{\eta }-\left(\acute{\eta }-2\right)}^F+\left(\frac{\acute{\eta }-2}{2}\right)\left[-36\acute{\gamma }+232\right]=262+\left(\acute{\eta }-2\right)\left[-18\acute{\gamma }+116\right]\hfill \\ \hfill & =\acute{\eta }\left[-18\acute{\gamma }+116\right]+36\acute{\gamma }+30\hfill \end{array}$

which completes the proof.

Theorem 4.2. For square-hexagonal kink chain ${}_{2}T_2$ with $\acute{\eta }$ number of kinks, we have

$E_{\acute{\eta }}^{GA}=\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.04662133\acute{\gamma }+6.455861185$

(b) For $\acute{\eta }=2n$; $n\in N$

$E_{\acute{\eta }}^{GA}=\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.09324266\acute{\gamma }+6.01305214$

Proof. Let $\acute{\eta }\ge 2$, then there are three possibilities. Using Table 3 and Equation 7, we get

$\mathit{1}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{1}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill GA{\left({}_{2}T_2^1\right)}_{\acute{\eta }}& ={\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\frac{\sqrt{6}}{5}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]+2\frac{\sqrt{2}}{3}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]\hfill \\ \hfill & +4\frac{\sqrt{3}}{7}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\hfill \end{array}$

$=GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+10.66990639(14)$

$\mathit{2}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{2}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill GA{\left({}_{2}T_2^2\right)}_{\acute{\eta }}& ={\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1+2\frac{\sqrt{6}}{5}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+2\frac{\sqrt{2}}{3}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]\hfill \\ \hfill & +4\frac{\sqrt{3}}{7}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\hfill \end{array}$

$=GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+10.73704477(15)$

$\mathit{3}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{3}})}_{\acute{\mathit{\eta }}}$, then

$GA{\left({}_{2}T_2^3\right)}_{\acute{\eta }}={\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2+2\frac{\sqrt{6}}{5}{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\frac{\sqrt{2}}{3}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+6\right]+4\frac{\sqrt{3}}{7}{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3$

$=GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+10.65685425(16)$

Thus, we have

$E_{\acute{\eta }}^{GA}=\acute{\gamma }GA{\left({}_{2}T_2^1\right)}_{\acute{\eta }}+\acute{\gamma }GA{\left({}_{2}T_2^2\right)}_{\acute{\eta }}+\left(1-2\acute{\gamma }\right)GA{\left({}_{2}T_2^3\right)}_{\acute{\eta }}$

Using Equations 14–16, we get the following relation

$E_{\acute{\eta }}^{GA}=\acute{\gamma }\left[GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+10.66990639\right]+\acute{\gamma }\left[GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+10.73704477\right]+\left(1-2\acute{\gamma }\right)\left[GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+10.65685425\right]$

$E_{\acute{\eta }}^{GA}=GA{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+0.09324266\acute{\gamma }+10.65685425$

Applying operator E on both sides and $\therefore E(E_{\acute{\eta }}^{GA})=E_{\acute{\eta }}^{GA}$

$E_{\acute{\eta }}^{GA}=E_{\acute{\eta }-2}^{GA}+0.09324266\acute{\gamma }+10.65685425$

$•$ Let $\acute{\eta }=2n-1$

For $n=1\Rightarrow \acute{\eta }=1$, $E_1=11.78428831$, which is indeed true. Using recursive relation upto $\acute{\eta }-1$ trerms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{GA}& =E_{\acute{\eta }-\left(\acute{\eta }-1\right)}^{GA}+\left(\frac{\acute{\eta }-1}{2}\right)\left[0.09324266\acute{\gamma }+10.65685425\right]\hfill \\ \hfill & =11.78428831+\left(\acute{\eta }-1\right)\left[0.04662133\acute{\gamma }+5.328427125\right]\hfill \\ \hfill & =\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.04662133\acute{\gamma }+6.455861185\hfill \end{array}$

which completes the result.

$•$ Let $\acute{\eta }=2n$

For $n=1\Rightarrow \acute{\eta }=2$, $E_2=16.66990639$, which is indeed true. Using recursive relation upto $\acute{\eta }-2$ terms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{GA}& =E_{\acute{\eta }-\left(\acute{\eta }-2\right)}^{GA}+\left(\frac{\acute{\eta }-2}{2}\right)\left[0.09324266\acute{\gamma }+10.65685425\right]\hfill \\ \hfill & =16.66990639+\left(\acute{\eta }-2\right)\left[0.04662133\acute{\gamma }+5.328427125\right]\hfill \\ \hfill & =\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.09324266\acute{\gamma }+6.01305214\hfill \end{array}$

which completes the proof.

Theorem 4.3. For square-hexagonal kink chain ${}_{2}T_2$ with $\acute{\eta }$ number of kinks, we have

$E_{\acute{\eta }}^{SC}=\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.032431259\acute{\gamma }+3.106204951$

(b) For $\acute{\eta }=2n$; $n\in N$

$E_{\acute{\eta }}^{SC}=\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.064862518\acute{\gamma }+3.021179965$

Proof. Let $\acute{\eta }\ge 2$, then there are three possibilities. Using Table 3 and Equation 8, we get

$\mathit{1}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{1}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill SC{\left({}_{2}T_2^1\right)}_{\acute{\eta }}& =\frac{1}{2}{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{\sqrt{5}}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]+\frac{1}{\sqrt{6}}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]\hfill \\ \hfill & +\frac{1}{\sqrt{7}}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+\frac{1}{2\sqrt{2}}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \end{array}$

$=SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4.53132988(17)$

$\mathit{2}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{2}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill SC{\left({}_{2}T_2^2\right)}_{\acute{\eta }}& =\frac{1}{2}\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]+\frac{1}{\sqrt{5}}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+\frac{1}{\sqrt{6}}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]\hfill \\ \hfill & +\frac{1}{\sqrt{7}}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+\frac{1}{2\sqrt{2}}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \end{array}$

$=SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4.553832468(18)$

$\mathit{3}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{3}})}_{\acute{\mathit{\eta }}}$, then

$=\frac{1}{2}\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+\frac{1}{\sqrt{5}}{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{\sqrt{6}}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+6\right]+\frac{1}{\sqrt{7}}{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{2\sqrt{2}}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]$

$SC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}=SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4.510149915(19)$

Thus, we have

$E_{\acute{\eta }}^{SC}=\acute{\gamma }SC{\left({}_{2}T_2^1\right)}_{\acute{\eta }}+\acute{\gamma }SC{\left({}_{2}T_2^2\right)}_{\acute{\eta }}+\left(1-2\acute{\gamma }\right)SC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}$

Using Equations 17–19, we get the following relation

$E_{\acute{\eta }}^{SC}=\acute{\gamma }\left[SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4.53132988\right]+\acute{\gamma }\left[SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4.553832468\right]+\left(1-2\acute{\gamma }\right)\left[SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4.510149915\right]$

$E_{\acute{\eta }}^{SC}=SC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+0.064862518\acute{\gamma }+4.510149915$

Applying operator E on both sides and $\therefore E(E_{\acute{\eta }}^{SC})=E_{\acute{\eta }}^{SC}$

$E_{\acute{\eta }}^{SC}=E_{\acute{\eta }-2}^{SC}+0.064862518\acute{\gamma }+4.510149915$

$•$ Let $\acute{\eta }=2n-1$; $n\in N$

For $n=1\Rightarrow \acute{\eta }=1$, $E_1=5.361279909$, which is indeed true. Using recursive relation upto $\acute{\eta }-1$ trerms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{SC}& =E_{\acute{\eta }-\left(\acute{\eta }-1\right)}^{SC}+\left(\frac{\acute{\eta }-1}{2}\right)\left[0.064862518\acute{\gamma }+4.510149915\right]\hfill \\ \hfill & =5.361279909+\left(\acute{\eta }-1\right)\left[0.032431259\acute{\gamma }+2.255074958\right]\hfill \\ \hfill & =\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.032431259\acute{\gamma }\hfill \\ \hfill & +3.106204951\hfill \end{array}$

which completes the result.

$•$ Let $\acute{=}2n$; $n\in N$

For $n=1\Rightarrow \acute{\eta }=2$, $E_2=7.53132988$, which is indeed true. Using recursive relation upto $\acute{\eta }-2$ terms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{SC}& =E_{\acute{\eta }-\left(\acute{\eta }-2\right)}^{SC}+\left(\frac{\acute{\eta }-2}{2}\right)\left[0.064862518\acute{\gamma }+4.510149915\right]\hfill \\ \hfill & =7.53132988+\left(\acute{\eta }-2\right)\left[0.032431259\acute{\gamma }+2.255074958\right]\hfill \\ \hfill & =\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.064862518\acute{\gamma }\hfill \\ \hfill & +3.021179965\hfill \end{array}$

which completes the proof.

Theorem 4.4. For square-hexagonal kink chain ${}_{2}T_2$ with $\acute{\eta }$ number of kinks, we have

(a) For $\acute{\eta }=2n-1$; $n\in N$

$E_{\acute{\eta }}^{\mathit{ABC}}=\left[0.014694163\acute{\gamma }+1.333193054\right]\acute{\eta }-0.014694163\acute{\gamma }+2.108399043$

(b) For $\acute{\eta }=2n$; $n\in N$

$E_{\acute{\eta }}^{\mathit{ABC}}=\left[0.014694163\acute{\gamma }+1.333193054\right]\acute{\eta }-0.029388326\acute{\gamma }+2.135405879$

Proof. Let $\acute{\eta }\ge 2$, then there are three possibilities. Using Table 3 and Equation 9, we get$\mathit{1}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{1}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill ABC{\left({}_{2}T_2^1\right)}_{\acute{\eta }}& =\frac{\sqrt{2}}{4}{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{\sqrt{3}}{6}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]\hfill \\ \hfill & +\frac{1}{4}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]\hfill \\ \hfill & +\frac{\sqrt{5}}{12}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+\frac{\sqrt{6}}{16}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \\ \hfill & =ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2.680471644\hfill \end{array}(20)$

$\mathit{2}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{2}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill ABC{\left({}_{2}T_2^2\right)}_{\acute{\eta }}& =\frac{\sqrt{2}}{4}\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]+\frac{\sqrt{3}}{6}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]\hfill \\ \hfill & +\frac{1}{4}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]+\frac{\sqrt{5}}{12}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]\hfill \\ \hfill & +\frac{\sqrt{6}}{16}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \\ \hfill & =ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2.681688898\hfill \end{array}(21)$

$\mathit{3}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{3}})}_{\acute{\mathit{\eta }}}$, then

$ABC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}=\frac{\sqrt{2}}{4}\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+\frac{\sqrt{3}}{6}{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{4}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+6\right]+\frac{\sqrt{5}}{12}{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{\sqrt{6}}{16}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]$

$ABC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}=ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2.666386108(22)$

Thus, we have

$E_{\acute{\eta }}^{\mathit{ABC}}=\acute{\gamma }ABC{\left({}_{2}T_2^1\right)}_{\acute{\eta }}+\acute{\gamma }ABC{\left({}_{2}T_2^2\right)}_{\acute{\eta }}+\left(1-2\acute{\gamma }\right)ABC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}$

Using Equations 20–22, we get the following relation

$E_{\acute{\eta }}^{\mathit{ABC}}=\acute{\gamma }\left[ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2.680471644\right]+\acute{\gamma }\left[ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2.681688898\right]+\left(1-2\acute{\gamma }\right)\left[ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2.666386108\right]$

$E_{\acute{\eta }}^{\mathit{ABC}}=ABC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+0.029388326\acute{\gamma }+2.666386108$

Applying operator E on both sides and $\therefore E(E_{\acute{\eta }}^{\mathit{ABC}})=E_{\acute{\eta }}^{\mathit{ABC}}$

$E_{\acute{\eta }}^{\mathit{ABC}}=E_{\acute{\eta }-2}^{\mathit{ABC}}+0.029388326\acute{\gamma }+2.666386108$

For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}-\mathit{1}$ For $n=1\Rightarrow \acute{\eta }=1$, $E_1=3.441592097$, which is indeed true. Using recursive relation upto $\acute{\eta }-1$ trerms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{\mathit{ABC}}& =E_{\acute{\eta }-\left(\acute{\eta }-1\right)}^{\mathit{ABC}}+\left(\frac{\acute{\eta }-1}{2}\right)\left[0.029388326\acute{\gamma }+2.666386108\right]\hfill \\ \hfill & =3.441592097+\left(\acute{\eta }-1\right)\left[0.014694163\acute{\gamma }+1.333193054\right]\hfill \\ \hfill & =\left[0.014694163\acute{\gamma }+1.333193054\right]\acute{\eta }-0.014694163\acute{\gamma }\hfill \\ \hfill & +2.108399043\hfill \end{array}$

which completes the result.

For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}$ For $n=1\Rightarrow \acute{\eta }=2$, $E_2=4.801791987$, which is indeed true. Using recursive relation upto $\acute{\eta }-2$ terms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{\mathit{ABC}}& =E_{\acute{\eta }-\left(\acute{\eta }-2\right)}^{\mathit{ABC}}+\left(\frac{\acute{\eta }-2}{2}\right)\left[0.029388326\acute{\gamma }+2.666386108\right]\hfill \\ \hfill & =4.801791987+\left(\acute{\eta }-2\right)\left[0.014694163\acute{\gamma }+1.333193054\right]\hfill \\ \hfill & =\left[0.014694163\acute{\gamma }+1.333193054\right]\acute{\eta }-0.029388326\acute{\gamma }\hfill \\ \hfill & +2.135405879\hfill \end{array}$

which completes the proof.

Theorem 4.5. For square-hexagonal kink chain ${}_{2}T_2$ with $\acute{\eta }$ number of kinks, we have

(a) For $\acute{\eta }=2n-1$; $n\in N$

$E_{\acute{\eta }}^{PC}=\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.016673376\acute{\gamma }+2.98179004$

(b) For $\acute{\eta }=2n$; $n\in N$

$E_{\acute{\eta }}^{PC}=\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.033346752\acute{\gamma }+3.003236649$

Proof. Let $\acute{\eta }\ge 2$, then there are three possibilities. Using Table 3 and Equation 10, we get

$\mathit{1}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{1}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill PC{\left({}_{2}T_2^1\right)}_{\acute{\eta }}& =\frac{1}{2}{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{\sqrt{6}}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]+\frac{1}{2\sqrt{2}}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+4\right]\hfill \\ \hfill & +\frac{1}{2\sqrt{3}}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+\frac{1}{4}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+1\right]\hfill \end{array}$

$=PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3.874556993(23)$

$\mathit{2}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{2}})}_{\acute{\mathit{\eta }}}$, then

$\begin{array}{cc}\hfill PC{\left({}_{2}T_2^2\right)}_{\acute{\eta }}& =\frac{1}{\sqrt{2}}\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{n-2}+1\right]+\frac{1}{\sqrt{6}}\left[{\beta }_{23}{\left({}_{2}T_2\right)}_{n-2}+3\right]\hfill \\ \hfill & +\frac{1}{2\sqrt{2}}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{n-2}+3\right]+\frac{1}{2\sqrt{3}}\left[{\beta }_{34}{\left({}_{2}T_2\right)}_{n-2}+3\right]\hfill \\ \hfill & +\frac{1}{4}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{n-2}+1\right]=PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3.901430447\hfill \end{array}(24)$

$\mathit{3}.$ If ${({}_{\mathit{2}}\mathit{T}_{\mathit{2}})}_{\acute{\mathit{\eta }}-\mathit{2}}\to {({}_{\mathit{2}}\mathit{T}_{\mathit{2}}^{\mathit{3}})}_{\acute{\mathit{\eta }}}$, then

$PC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}=\frac{1}{2}\left[{\beta }_{22}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+2\right]+\frac{1}{\sqrt{6}}{\beta }_{23}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{2\sqrt{2}}\left[{\beta }_{24}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+6\right]+\frac{1}{2\sqrt{3}}{\beta }_{34}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+\frac{1}{4}\left[{\beta }_{44}{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3\right]$

$PC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}=PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3.871320344(25)$

Thus, we have

$E_{\acute{\eta }}^{PC}=\acute{\gamma }PC{\left({}_{2}T_2^1\right)}_{\acute{\eta }}+\acute{\gamma }PC{\left({}_{2}T_2^2\right)}_{\acute{\eta }}+\left(1-2\acute{\gamma }\right)PC{\left({}_{2}T_2^3\right)}_{\acute{\eta }}$

Using Equations 23–25, we get the following relation

$E_{\acute{\eta }}^{PC}=\acute{\gamma }\left[PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3.874556993\right]+\acute{\gamma }\left[PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3.901430447\right]+\left(1-2\acute{\gamma }\right)\left[PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+3.871320344\right]$

$E_{\acute{\eta }}^{PC}=PC{\left({}_{2}T_2\right)}_{\acute{\eta }-2}+0.033346752\acute{\gamma }+3.871320344$

Applying operator E on both sides and $\therefore E(E_{\acute{\eta }}^{PC})=E_{\acute{\eta }}^{PC}$

$E_{\acute{\eta }}^{PC}=E_{\acute{\eta }-2}^{PC}+0.033346752\acute{\gamma }+3.871320344$

For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}-\mathit{1}$ For $n=1\Rightarrow \acute{\eta }=1$, $E_1=4.917450212$, which is indeed true. Using recursive relation upto $\acute{\eta }-1$ trerms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{PC}& =E_{\acute{\eta }-\left(\acute{\eta }-1\right)}^{PC}+\left(\frac{\acute{\eta }-1}{2}\right)\left[0.033346752\acute{\gamma }+3.871320344\right]\hfill \\ \hfill & =4.917450212+\left(\acute{\eta }-1\right)\left[0.016673376\acute{\gamma }+1.935660172\right]\hfill \\ \hfill & =\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.016673376\acute{\gamma }+2.98179004\hfill \end{array}$

which completes the result.

For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}$ For $n=1\Rightarrow \acute{\eta }=2$, $E_2=6.874556993$, which is indeed true. Using recursive relation upto $\acute{\eta }-2$ terms

$\begin{array}{cc}\hfill E_{\acute{\eta }}^{PC}& =E_{\acute{\eta }-\left(\acute{\eta }-2\right)}^{PC}+\left(\frac{\acute{\eta }-2}{2}\right)\left[0.033346752\acute{\gamma }+3.871320344\right]\hfill \\ \hfill & =6.874556993+\left(\acute{\eta }-2\right)\left[0.016673376\acute{\gamma }+1.935660172\right]\hfill \\ \hfill & =\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.033346752\acute{\gamma }+3.003236649\hfill \end{array}$

which completes the proof.

From Figure 3 it is easy to that three possible kink chains can be obtained from ${({}_{2}T_2^{\acute{\gamma }})}_{\acute{\eta }}$ by taking the value of $\acute{\gamma }=\frac{1}{3}$.

Corollary 1. If $\acute{\eta }=2n-1$; $n\in N$ then at ${(\acute{\eta }-2)}^{th}$ stage

$•F=110(\acute{\eta }-2)+284$

$•GA=5.343967568(\acute{\eta }-2)+17.12825588$

$•SC=2.265885378(\acute{\eta }-2)+7.627165287$

$•ABC=1.338091108(\acute{\eta }-2)+4.779683205$

$•PC=1.941217964(\acute{\eta }-2)+6.858668176$

Corollary 2. If $\acute{\eta }=2n$; $n\in N$ then at ${(\acute{\eta }-2)}^{th}$ stage

$•F=110(\acute{\eta }-2)+262$

$•GA=5.343967568(\acute{\eta }-2)+16.66990639$

$•SC=2.265885378(\acute{\eta }-2)+7.531329882$

$•ABC=1.338091108(\acute{\eta }-2)+4.801791986$

$•PC=1.941217964(\acute{\eta }-2)+6.874556993$

4.1 Analytical comparison at ${(\acute{\eta }-2)}^{th}$ stage

In this section we analytically prove that forgotten index attains the greatest expected values at ${(\acute{\eta }-2)}^{th}$ stage, for any value of $\acute{\gamma }$ and $\acute{\eta }$ and for $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$, while atom-bond connectivity attains minimum expectations.

Corollary 3. For $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$; $n\in N$, we have

$E\left[F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]$

Proof. $•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}-\mathit{1}$

$\begin{array}{cc}\hfill E\left[F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]& =\left\{\acute{\eta }\left[-18\acute{\gamma }+116\right]+18\acute{\gamma }+58\right\}\hfill \\ \hfill & -\left\{\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]\right.\hfill \\ \hfill & \left.-0.04662133\acute{\gamma }+6.455861185\right\}\hfill \\ \hfill & =18.04662133\acute{\gamma }\left(1-\acute{\eta }\right)+110.6715729\acute{\eta }\hfill \\ \hfill & +51.54413881>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

$•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}$

$\begin{array}{c}E\left[F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ =\left\{\acute{\eta }\left[-18\acute{\gamma }+116\right]+36\acute{\gamma }+30\right\}\hfill \\ -\left\{\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.09324266\acute{\gamma }+6.01305214\right\}\hfill \\ =18.04662133\acute{\gamma }\left(2-\acute{\eta }\right)+110.6715783\acute{\eta }+23.98694786>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

Corollary 4. For $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$; $\acute{\eta }\in N$, we have

$E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]$

Proof. $•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}-\mathit{1}$

$\begin{array}{c}E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ =\left\{\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.04662133\acute{\gamma }+6.455861185\right\}\hfill \\ -\left\{\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.032431259\acute{\gamma }+3.106204951\right\}\hfill \\ =0.014190071\acute{\gamma }\left(\acute{\eta }-1\right)+3.073352167\acute{\eta }+3.349656234>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

$•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}$

$\begin{array}{c}E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ =\left\{\acute{\eta }\left[0.04662133\acute{\gamma }+5.328427125\right]-0.09324266\acute{\gamma }+6.01305214\right\}\hfill \\ -\left\{\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.064862518\acute{\gamma }+3.021179965\right\}\hfill \\ =0.014190071\acute{\gamma }\left(\acute{\eta }-2\right)+3.073352167\acute{\eta }+2.991872175)>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

Corollary 5. For $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$; $\acute{\eta }\in N$, we have

$E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]$

Proof. $•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}-\mathit{1}$

$\begin{array}{c}\hfill E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\\ =\left\{\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.032431259\acute{\gamma }+3.106204951\right\}\hfill \\ -\left\{\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.016673376\acute{\gamma }+2.98179004\right\}\hfill \\ =0.015757883\acute{\gamma }\left(\acute{\eta }-1\right)+0.319414786\acute{\eta }+0.124414911)>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

$•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}$

$\begin{array}{c}E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ =\left\{\acute{\eta }\left[0.032431259\acute{\gamma }+2.255074958\right]-0.064862518\acute{\gamma }+3.021179965\right\}\hfill \\ -\left\{\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.033346752\acute{\gamma }+3.003236649\right\}\hfill \\ =0.015757883\acute{\gamma }\left(\acute{\eta }-2\right)+0.319414786\acute{\eta }+0.017943316>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

Corollary 6. For $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$; $\acute{\eta }\in N$, we have

$E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[ABC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]$

Proof. $•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}-\mathit{1}$

$\begin{array}{c}E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[ABC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ =\left\{\acute{\eta }\left[0.016673376\acute{\gamma }+1.935660172\right]-0.016673376\acute{\gamma }+2.98179004\right\}\hfill \\ -\left\{\left[0.014694163\acute{\gamma }+1.333193054\right]\acute{\eta }-0.014694163\acute{\gamma }+2.108399043\right\}\hfill \\ =0.001979213\acute{\gamma }\left(\acute{\eta }-1\right)+0.602467118\acute{\eta }+0.873390997>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[ABC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

$•$ For $\acute{\mathit{\eta }}=\mathit{2}\mathit{n}$

$\begin{array}{c}E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]-E\left[ABC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ =\left\{\left[0.016673376\acute{\gamma }+1.935660172\right]\acute{\eta }-0.033346752\acute{\gamma }+3.003236649\right\}\hfill \\ -\left\{\left[0.014694163\acute{\gamma }+1.333193054\right]\acute{\eta }-0.029388326\acute{\gamma }+2.135405879\right\}\hfill \\ =0.001979213\acute{\gamma }\left(\acute{\eta }-2\right)+0.602467118\acute{\eta }+0.86783077>0\hfill \end{array}$

which holds for $\acute{\gamma }=\frac{1}{3}$ and for all $\acute{\eta }\in N$, so we have

$\begin{array}{c}\hfill E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[ABC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\end{array}$

The above corollaries implies that;

Corollary 7.

$\begin{array}{cc}\hfill E\left[F{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]& >E\left[GA{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[SC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]>E\left[PC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \\ \hfill & >E\left[ABC{\left({}_{2}T_2^{\acute{\gamma }}\right)}_{\acute{\eta }}\right]\hfill \end{array}$

From these analytical expressions, we conclude that that the expected value of Forgotten index for $\acute{\gamma }=\frac{1}{3}$ is greatest among all other computed topological indices at ${(\acute{\eta }-2)}^{th}$ stage.

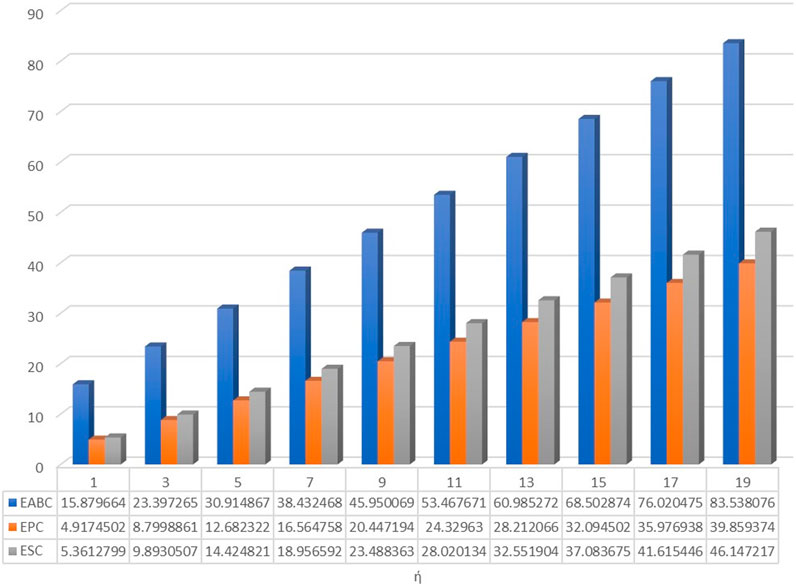
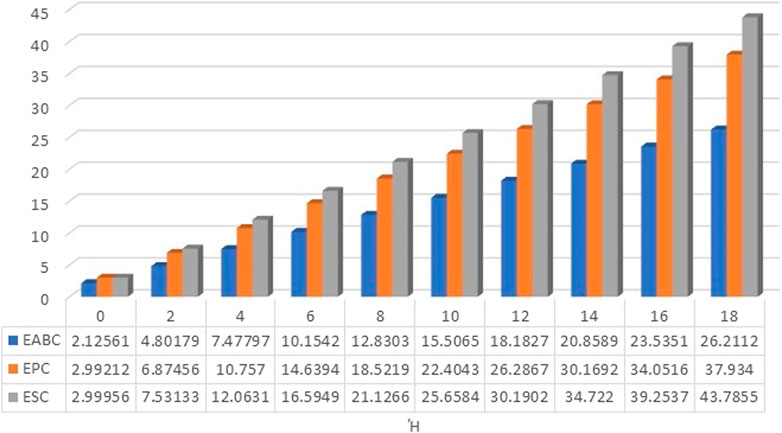
4.2 Graphical comparison of expected values of topological indices at ${(\acute{\eta }-2)}^{th}$ stage

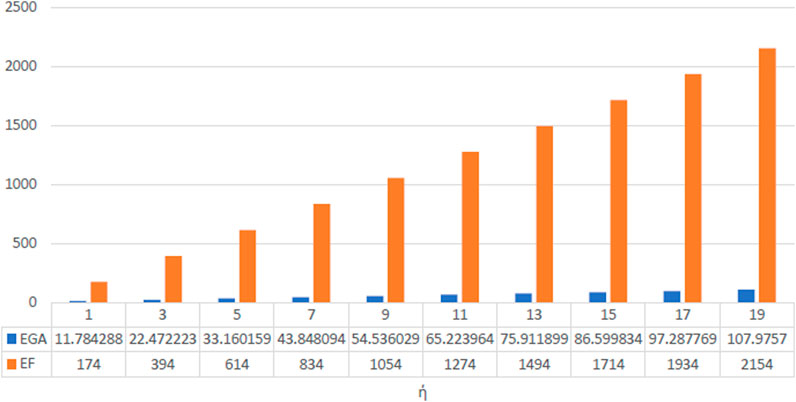
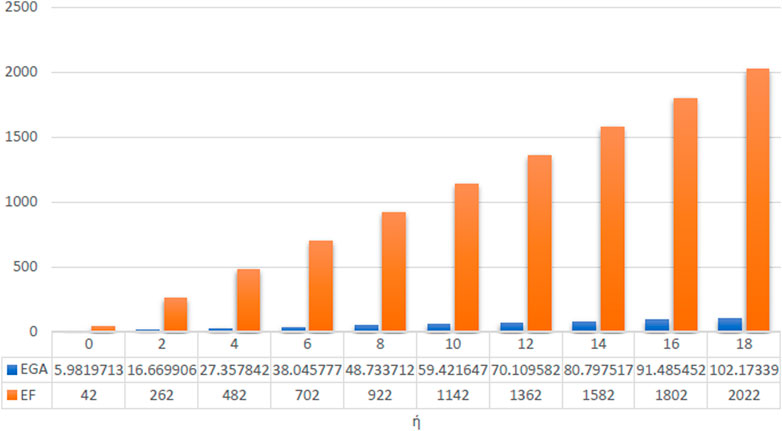
The numerical values as well as graphical representation in Figures 4–7 meet with the results of analytical comparison. So, we conclude that the expected value of $F$ index reaches maximum value for both odd and even numbered kinked chains at ${(\acute{\eta }-2)}^{th}$ stage. And the expected value of $ABC$ index for both odd and even numbered kinked chains attains minimum value at ${(\acute{\eta }-2)}^{th}$ stage, and for $\acute{\gamma }=\frac{1}{3}$.

Figure 4

Figure 4. Expected values of $PC$, $ABC$ and $SC$ at ${(\acute{\eta }-2)}^{th}$ stage for $\acute{\eta }=2n-1$.

Figure 5

Figure 5. Expected values of $PC$, $ABC$ and $SC$ at ${(\acute{\eta }-2)}^{th}$ stage for $\acute{\eta }=2n$.

Figure 6

Figure 6. Expected values of $F$ and $GA$ at ${(\acute{\eta }-2)}^{th}$ stage for $\acute{\eta }=2n-1$.

Figure 7

Figure 7. Expected values of $F$ and $GA$ at ${(\acute{\eta }-2)}^{th}$ stage for $\acute{\eta }=2n$.

5 Conclusion

In conclusion, at the ${(\acute{\eta }-2)}^{th}$ stage, the expected value of a certain topological descriptor for three kink chains with $\acute{\eta }=2n-1$ is equal to the average of the corresponding topological descriptor for $\acute{\eta }=2n-1$, and similarly, the expected value of the topological descriptor for $\acute{\eta }=2n$ equals the average for $\acute{\eta }=2n$. This establishes the validity of the results. The values of the topological descriptors ${\mathfrak{R}}_1$, ${\mathfrak{R}}_2$, $HZ$, $Re{Z}_2$, $G{O}_1$, and $G{O}_2$ can be calculated using the theorems proven above for $\acute{\gamma }=\frac{1}{3}$ at the ${(\acute{\eta }-2)}^{th}$ stage. Furthermore, at this stage, for both $\acute{\eta }=2n-1$ and $\acute{\eta }=2n$, the expected values of the descriptors $E_{{\mathfrak{R}}_1}^{\acute{\eta }}$, $E_{{\mathfrak{R}}_2}^{\acute{\eta }}$, $E_{HZ}^{\acute{\eta }}$, $E_{Re{Z}_2}^{\acute{\eta }}$, $E_{G{O}_1}^{\acute{\eta }}$, and $E_{G{O}_2}^{\acute{\eta }}$ depend on both $\acute{\gamma }$ and the number of kinks $\acute{\eta }$. However, the expected value of $Re{Z}_1$ depends solely on the number of kinks $\acute{\eta }$ and is identical in both cases. Moreover, the expected values for the forgotten index attains maximum value, whereas those for the ABC index attains minimum value, for both the cases.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XL: Funding acquisition, Investigation, Formal analysis, Validation, Writing – review and editing. AR: Conceptualization, Formal Analysis, Investigation, Validation, Writing – review and editing. MK: Conceptualization, Formal Analysis, Investigation, Validation, Writing – original draft. SK: Conceptualization, Investigation, Methodology, Validation, Writing – review and editing. SN: Conceptualization, Investigation, Validation, Writing – review and editing. RN: Conceptualization, Investigation, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [KFU251155] and Anhui Province quality Engineering” online and offline mixed and Social practice course” (2020xsxxkc222) Scientific Research Program of Colleges and Universities in Anhui Province (2022AH052889, 2024AH050616).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Alraqad TA, Saber H, Ali A, Mazorodze JP. On-bond incident degree indices of square-hexagonal chains. J Mathematics (2022) 2022(1):1864828. doi:10.1155/2022/1864828

CrossRef Full Text | Google Scholar

2. Sigarreta SC, Sigarreta SM, Cruz-Suarez H. On degree-based topological indices of random polyomino chains. Math Biosciences Eng (2022) 19(9):8760–73. doi:10.3934/mbe.2022406

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Xiao L, Chen S, Guo Z, Chen Q. The geometric-arithmetic index of benzenoid systems and phenylenes. Int J Contemp Math Sci (2010) 5(45):2225–2230.

Google Scholar

4. Zhou B, Trinajstic N. Relations between the product-and sum-connectivity indices. Croatica chemica acta (2012) 85(3):363–365.

CrossRef Full Text | Google Scholar

5. Furtula B, Gutman I. A forgotten topological index. J Math Chem (2015) 53(4):1184–90. doi:10.1007/s10910-015-0480-z

CrossRef Full Text | Google Scholar

6. Gao W, Husin MN, Farahani MR, Imran M. On the edges version of atom-bond connectivity index of nanotubes. J Comput Theor Nanoscience (2016) 13(10):6733–40. doi:10.1166/jctn.2016.5621

CrossRef Full Text | Google Scholar

7. Trinajstic N. Chemical graph theory. Boca Raton: CRC Press (1992).

Google Scholar

8. Raza Z. The expected values of arithmetic bond connectivity and geometric indices in random phenylene chains. Heliyon (2020) 6(7):e04479. doi:10.1016/j.heliyon.2020.e04479

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wei L, Bian H, Yu H, Ding J. The expected values of Merrifield-Simmons index in random phenylene chains. Iran J Math (2020) 11(4):271–81.

Google Scholar

10. Fang X, You L, Liu H. The expected values of Sombor indices in random hexagonal chains, phenylene chains and Sombor indices of some chemical graphs. Int J Quan Chem. (2021) 121(17):e26740. doi:10.1002/qua.26740

CrossRef Full Text | Google Scholar

11. Ke X, Wei S, Huang J. The atom-bond connectivity and geometric-arithmetic indices in random polyphenyl chains. Polycyclic Aromatic Compounds (2021) 41(9):1873–82. doi:10.1080/10406638.2019.1703763

CrossRef Full Text | Google Scholar

12. Raza Z. The expected values of some indices in random phenylene chains. The Eur Phys J Plus (2021) 136(1):91–15. doi:10.1140/epjp/s13360-021-01082-y

CrossRef Full Text | Google Scholar

13. Raza Z, Akhter S, Shang Y. Expected value of first Zagreb connection index in random cyclooctatetraene chain, random polyphenyls chain, and random chain network. Front Chem (2023) 10:1067874. doi:10.3389/fchem.2022.1067874

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hayat S. Distance-based graphical indices for predicting thermodynamic properties of benzenoid hydrocarbons with applications. Comput Mater Sci (2023) 230:112492. doi:10.1016/j.commatsci.2023.112492

CrossRef Full Text | Google Scholar

15. Hayat S, Mahadi H, Alanazi SJ, Wang S. Predictive potential of eigenvalues-based graphical indices for determining thermodynamic properties of polycyclic aromatic hydrocarbons with applications to polyacenes. Comput Mater Sci (2024) 238:112944. doi:10.1016/j.commatsci.2024.112944

CrossRef Full Text | Google Scholar

16. Hayat S, Khan A, Ali K, Liu JB. Structure-property modeling for thermodynamic properties of benzenoid hydrocarbons by temperature-based topological indices. Ain Shams Eng J (2024) 15(3):102586. doi:10.1016/j.asej.2023.102586

CrossRef Full Text | Google Scholar

17. Chunsong B, Khalil M, Razzaque A, Kanwal S, Nazir R, Noor S. Exploring structural variations and topological descriptors of square-hexagonal kink chains of type T_2,2 in engineering applications. Adv Mech Eng (2024) 16(10):16878132241290418. doi:10.1177/16878132241290418

CrossRef Full Text | Google Scholar

18. Chen R, Razzaque A, Khalil M, Kanwal S, Noor S, Nazir R. Expected value of topological descriptors for possible kink chains of type ₂T₂. Front Chem (2024) 12:1517892. doi:10.3389/fchem.2024.1517892

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Garcia-Domenech R, Galvez J, de Julian-Ortiz JV, Pogliani L. Some new trends in chemical graph theory. Chem Rev (2008) 108(3):1127–69. doi:10.1021/cr0780006

PubMed Abstract | CrossRef Full Text | Google Scholar