- 1Department of Psychology, College of Arts & Sciences, University of Oregon, Eugene, OR, United States
- 2Department of Education Studies, College of Education, University of Oregon, Eugene, OR, United States
This paper connects two research traditions—social psychology's examination of inferential accuracy, and educational research on teacher cognition and decision-making, in order to consider how teachers attempt to accurately infer their students' thoughts and feelings during instruction. Our aim is to link the social psychological study of inferential accuracy with several prominent educational constructs related to teacher expertise. We begin by introducing inferential accuracy and providing a brief overview of social psychology research about it. We suggest that inferential accuracy may affect teacher decisions in what are known as “discretionary spaces” in classroom settings. Next, we delineate similarities and differences between inferential accuracy and two constructs related to teacher expertise (diagnostic competence and teacher noticing). We then identify the parallels between inferential accuracy and two other educational constructs—pedagogical content knowledge and informal formative assessment. Throughout this synthesis, we consider applications of inferential accuracy research to inform how, and how well, teachers may be able to infer their students' thoughts and feelings during instruction, as well as the ways that social psychology researchers may consider teacher-student classroom interactions as fruitful settings in which to examine interpersonal accuracy. We point out the educational constructs that correspond to social psychological predictors of inferential accuracy, discuss areas of tension when translating inferential accuracy research into educational contexts, and suggest future research questions that may prove fruitful with interdisciplinary collaboration.
Introduction
How do teachers know the right thing to do next in the classroom? The methods of defining, operationalizing, and measuring teacher expertise are as varied as the tasks teachers undertake before, during, and after instruction (Anderson and Taner, 2023; Berliner, 2001; Bromme, 2001; Clarke et al., 2011; Dunham, 2002; Eraut, 2007; Gotwals et al., 2015; Hattie, 2009; Palmer et al., 2005; Ropo, 2004; Shulman, 2000; Tsui, 2005, 2009; van Dijk et al., 2020). One particularly difficult-to-study aspect of teacher expertise is how teachers make moment-to-moment decisions not structured within a predetermined lesson plan—decisions that are in part informed by teachers' inferences about what is going on in the heads of their students (e.g., choosing which student to call on, deciding how to address misbehavior, or determining whether to move forward with a lesson in lieu of taking extra time to review a concept). Navigating these rapid-fire decisions, called discretionary spaces (Ball, 2018), requires teachers to recruit a diverse set of pedagogical, socio-emotional, and interpersonal skills and knowledge (e.g., pedagogical content knowledge, individuated knowledge about their students, meta-awareness of how they are perceived by the class).
In this conceptual analysis, we review social psychological research on inferential accuracy (the accurate inference of a target's thoughts and/or feelings, Hodges et al., 2024, 2015; Ickes et al., 1990), which has (to our knowledge) never been examined in the context of teachers during instruction. Inferential accuracy may offer a unique perspective for education researchers to examine how discretionary space choices and other classroom decisions are informed by teachers' inferences about students' dynamic thoughts and feelings. We first introduce inferential accuracy with a brief background and then recount an example of two discretionary spaces from an elementary school math class to provide an illustration and context for our discussions of educational and psychological constructs. We discuss grain-size as a means of contrasting inferential accuracy with two similar constructs from education research, diagnostic competence and teacher noticing (Ball, 2018; Wilson, 2024). We next examine the overlap and tension between inferential accuracy and two educational constructs related to teacher expertise: pedagogical content knowledge and informal formative assessment. In addition, we identify educational constructs that correspond to social psychological predictors of inferential accuracy to orient the reader to inferential accuracy's possible place in classroom research. We also discuss areas of tension when translating inferential accuracy research into educational contexts and suggest future research questions that may prove fruitful with interdisciplinary collaboration. Throughout the paper, we seek to build a bridge between one form of interpersonal accuracy studied by social psychology (inferential accuracy) and several prominent educational constructs reflective of teacher expertise in pedagogical contexts. These educational constructs are themselves wide-reaching and heterogeneous and so we limit the main focus of this paper to a conceptual review of their relation to inferential accuracy.
Inferential accuracy
Inferential accuracy is the accurate inference by one person (the “perceiver”) of another person's (the “target's”) thoughts and feelings during a social interaction (Hodges et al., 2015; Ickes, 2016). It has historically been referred to as “empathic accuracy,” although recent calls (e.g., Hodges et al., 2024) have suggested moving away from this term because it incorrectly suggests that this accuracy always leads to prosocial outcomes (Consider, as an example, a poker player who uses inferential accuracy to aid in taking an opponent's money). Within the focus of the current manuscript, we view teachers as perceivers (i.e., the ones inferring someone else's thoughts) and students as targets (i.e., the ones whose thoughts are inferred). Although inferences likely occur in both directions (i.e., students may also attempt to infer the thoughts and feelings of their teachers; see Gleason et al., 2009), the current paper is specifically interested in teacher inferences of students' thoughts and feelings.
The Ickes paradigm
The most common paradigm for studying inferential accuracy was developed by William Ickes and colleagues and first appeared in publications in the 1990s (Ickes et al., 1990). In this paradigm, two participants—i.e., a “dyad,” (defined as a group consisting of two people, particularly two people in a social interaction1)—engage in a video-recorded verbal interaction. Immediately following the interaction, one participant (the target) watches the video, which is paused intermittently at which times the targets report what they were thinking and feeling. The intermittent pauses may occur when the target reports remembering discrete thoughts/feelings or at predetermined intervals (e.g., every 30 s). The other participant (the perceiver) then watches the video of the interaction and, at the times when the target reported their thoughts and feelings, the perceiver is asked to infer—and provide in writing—their best guess of what the target was thinking at that moment (Gesn and Ickes, 1999; Ickes, 2016; Ickes et al., 1990). These thoughts and feelings—reported by the target and inferred by the perceiver—are then compared and rated for accuracy on a 3-point or 4-point scale by a team of coders.
The Ickes paradigm has developed into two sub-paradigms, both of which are relevant to the points we make in this paper, as both share the fundamental element of a perceiver inferring the thoughts and feelings of a target person, which we believe is the key ingredient that makes inferential accuracy interesting to contemplate in classrooms. In the dyadic interaction paradigm, the perceiver infers the thoughts and feelings of a target with whom they just interacted. In the standard stimulus paradigm, the perceivers can infer the thoughts and feelings of a target with whom they do not directly interact; instead, the target is viewed in a video recording interacting with another conversation partner (e.g., see Marangoni et al., 1995). In the standard stimulus paradigm, targets still re-watch their own videos to report their thoughts and feelings, but perceivers can be recruited to watch those videos and to infer the targets' thoughts and feelings at research sessions in the future, at times and in settings far removed from those at which the interaction in the video initially took place. Researchers use these different paradigms for different purposes (e.g., the standard stimulus paradigm aids in identifying target-level effects by having multiple perceivers view a single target; it also provides a standard test of accuracy, allowing comparison of different categories of perceivers or perceivers taking part under different conditions. The dyadic interaction paradigm allows for the examination of variables related to the target and perceiver's unique relationship—e.g., its length and quality.
Predictors of inferential accuracy
Although target characteristics can contribute to accuracy (Human and Biesanz, 2013; Lewis, 2014), the predominant focus of past inferential accuracy research has been identifying predictors of accuracy associated with the perceiver (i.e., what makes a good “mind-reader”). From this work, three predictors of perceiver accuracy have garnered robust empirical support: (1) the perceiver's familiarity with the target; (2) the use of cognitive schemas when making inferences; and (3) the use of verbal information from the target. Although inferential accuracy between teachers and students has not been studied in the context of education, each of these sources of accuracy correspond to a construct within teacher expertise, suggesting that expert teachers should be more accurate in inferring their students' thoughts in discretionary spaces.
First, familiarity with the target improves accuracy: friends are better at inferring a target's thoughts and feelings than strangers (Stinson and Ickes, 1992) and inferential accuracy generally increases as perceivers see more of a target (Marangoni et al., 1995). Curiously, in zero-acquaintance education research (studies conducted where teachers are unfamiliar with the students, e.g., Bhowmik et al., 2025), teachers' accuracy for students' stable characteristics after seeing a 30-s video is comparable to their accuracy in a natural classroom, suggesting that their expertise allows for accurate, rapid-fire judgments of stable characteristics or student characteristic profiles (Nickerson, 1999; Seidel et al., 2021). As described above, however, the relationship between a teacher's familiarity with their students and their accuracy for variable emotions or specific thought content at the level at which they are studied in inferential accuracy (e.g., every 30 s) remains understudied (Borko et al., 2008).
Second, incorporating schemas about people (and more specifically schemas that are actually validly informative) into inferences about a specific target's thoughts and feelings is related to increased accuracy (Hodges and Kezer, 2021; Lewis et al., 2012; Stinson and Ickes, 1992). “Informative schemas” are schemas about people that are made up of accurate information about a particular individual (Stinson and Ickes, 1992) or about categories of people (Lewis et al., 2012)2. As we discuss in detail later, schemas in educational contexts associated with increased accuracy may include a teacher's generalizations about how students at a particular developmental stage or who come from a certain kind of educational background may encounter common pitfalls when learning a specific topic—in other words, drawing on teachers' pedagogical content knowledge.
Third, the utilization of verbal information from the target (i.e., what the target says) corresponds to higher inferential accuracy. Multiple studies have shown that access to the target's words leads to higher accuracy—even in the absence of the video of the target (Gesn and Ickes, 1999; Hall and Schmid Mast, 2007; Hodges and Kezer, 2021; Kraus, 2017). Generally, attending to and using what targets say improves inferential accuracy in part because target speech tends to correspond to what targets are thinking (Hodges and Kezer, 2021). In the classroom, explicitly asking targets (students) to verbalize what they are thinking is a well-supported pedagogical tool that is a part of informal formative assessment, which we discuss below. Armed with this basic overview of how inferential accuracy has been studied, and importantly, sources of information that perceivers may use to accurately infer a target's thoughts, we now consider the educational concept of “discretionary spaces” and the decisions that teachers make in these spaces, to illustrate how inferential accuracy is likely to be reflected in student-teacher interactions within the classroom.
Discretionary spaces
To illustrate the concept of discretionary spaces, we offer the case study Deborah Ball (2018) presented in her presidential address to the American Educational Research Association. In this example, an expert teacher (Ball herself) leads a math lesson about locating fractions on a number line in an American elementary school classroom. Ball begins by noting that this lesson is often difficult for students due to the inconsistency between how number lines are presented (as consisting of whole numbers) and how fractions are visualized (as parts or “slices” of pizzas and pies). The students in Ball's example are tasked with identifying the fraction, 3/4, which is pointed out by an arrow on a number line (Figure 1). One student is called on and reports that she labeled the fraction 7/8. Although incorrect, her answer demonstrates a common pitfall for students in the lesson: counting all dashes on the number line instead of anchoring at zero. This first student's explanation is interrupted by a second student who asks, “why'd you choose seven-eighths?”
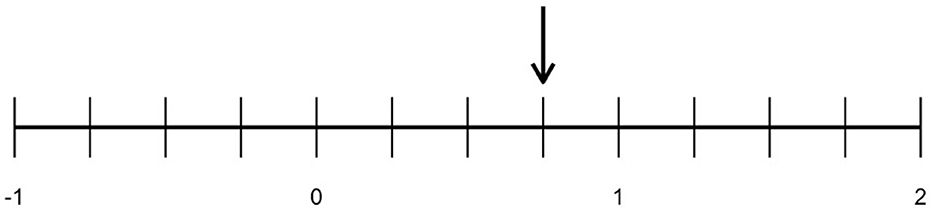
Figure 1. Fraction and number line task adapted from Ball (2018).
Ball identifies 22 unique discretionary spaces in an 88-s portion of this math lesson. Although Ball does not specifically describe inferring either student's thoughts or feelings as part of her proximal deliberation when navigating these discretionary spaces, we saw two examples of how Ball's expertise informed her inferences of students' thoughts, which in turn influenced Ball's decisions: (1) Ball infers the first student's reasoning as illustrative of a common misconception and thus worth exploring with the class, and (2) Ball infers that the second student's interruption was caused by mathematical curiosity (not an attempt to taunt the first student for answering incorrectly) and so does not reprimand her. Although both decisions reflect Ball's pedagogical content knowledge and are made in service of overarching pedagogical goals, they are also made in a distinctly social context and require Ball to leverage socio-emotional and interpersonal skills and knowledge.
In the first discretionary space, Ball infers a student's thinking as exemplary of a common misconception, an accurate inference informed by her pedagogical content knowledge (discussed below). An inaccurate inference in that moment (perhaps made by a novice teacher) may have missed the cues to this student's thinking and overlooked an opportunity for collaborative learning. This discretionary space is complicated by the socio-emotional risks Ball takes in asking the student to share her erroneous thinking with the class. Accurately inferring the student's current thoughts and feelings may support a positive pedagogical opportunity in which the student shares willingly or is appropriately pushed beyond her comfort zone to speak in front of the class. However, given the many social, emotional, and academic pressures students feel when participating in math classes (e.g., Ashcraft, 2002; Good et al., 2012), inaccuracy could result in Ball requesting a student who may be frustrated with the lesson or insecure in their feelings of belonging to share a wrong answer publicly and feel humiliated or picked on, jeopardizing Ball's positive teacher-student relationship with that student (e.g., Klassen et al., 2012).
The second discretionary space requires Ball to leverage very different information to determine whether to reprimand the interrupting student or encourage a dialogue between her and the first student. This decision likely incorporates Ball's knowledge of both students' individual thinking, knowledge of the students' relationships to one another and to the other students in the class, and knowledge of classroom protocols (e.g., the second student raised her hand prior to speaking but did not wait to be called on). Ball opts not to reprimand this second student, accurately inferring that she was genuinely curious about the first student's thinking. Inappropriately reprimanding the student risks punishing her for expressing mathematical curiosity, but failing to intervene if the second student were taunting the first risks the first student's feelings. In both cases, improper action risks harming a student's feelings of belonging (Good et al., 2012; Lewis and Hodges, 2015).
These discretionary spaces require Ball to incorporate a wide variety of prior information and proximal cues when making pedagogical decisions. Yet, they are only a few seconds apart, occur at the same level of analysis (i.e., they both constitute one discretionary space), and both clearly reflect her expertise. In our examination of several lines of education research (discussed below), no prior studies have collected reports of what students were thinking and feeling in discretionary spaces such as these. This may be a missed opportunity, as by examining students' thoughts and feelings in discretionary spaces and comparing them to teacher inferences, researchers may access a novel operationalization of teacher expertise that can begin to demonstrate how teachers' personal and enacted pedagogical content knowledge impacts the accuracy of their inferences about students and which in turn influences the effectiveness of their judgments and actions in the classroom.
Grain-size
To think about inferential accuracy in the classroom, we must consider the concept of grain-size. “Grain-size” is used in describing empirical research to differentiate levels and schedules of measurement—for example, to contrast large grain-size methods (e.g., teacher judgments as they are shaped over an entire academic year, Meissel et al., 2017) with small grain-size methods (e.g., measures of teachers' blood-oxygen level or heart-rate variability during classroom instruction that are taken every few seconds, Donker et al., 2023; Tobin et al., 2016; Wettstein et al., 2024). Grain-size encompasses not only the frequency of measurements but the scope and scale of the measures as well—it may include fine-tuned data such as heart-rate variability or complex, qualitative data from a teacher's reflections on a year of teaching.
The grain-size associated with discretionary spaces is particularly tricky for researchers as it encompasses moment-to-moment data for both teacher thinking and student experiences. In the case study example featured earlier in this paper, how researchers examine the second discretionary space (the student's interruption) may include recording data on Ball's proximal cognition of that student's rationale for interrupting her classmate and what the student is thinking in that moment (i.e., whether the student was taunting or positively engaging with her classmate).
At first glance, inferential accuracy in classroom contexts may seem to be already covered by two core constructs within teacher expertise: diagnostic competence (also referred to as diagnostic judgments or teacher judgment accuracy, Heitzmann et al., 2019; Helmke and Schrader, 1987; Loibl et al., 2020; Südkamp et al., 2012; Urhahne and Wijnia, 2021) and teacher noticing (also called professional vision, Jacobs et al., 2010; König et al., 2022; Sherin, 2014; Sherin et al., 2011). However, when considered in conjunction with grain-size, we believe that inferential accuracy taps into a precise—and understudied—empirical niche.
Diagnostic competence
Diagnostic competence most often refers to a teacher's accurate judgment of comparatively stable characteristics, such as students' academic achievement. It is often assessed by comparing teacher judgments to standardized test scores (Demaray and Elliot, 1998; Helmke and Schrader, 1987; Südkamp et al., 2012), reading ability (Beswick et al., 2005) or student cognitive ability measures (Machts et al., 2016). Some work has examined diagnostic competence for more dynamic processes, such as learning behaviors (Klug et al., 2016) or accurate judgments of the appropriateness, difficulty, and applicability of a task for a specific learning outcome (for a review, see Urhahne and Wijnia, 2021). However, even though the characteristics that are often studied as part of diagnostic competence (e.g., reading ability, achievement) change over time, they can be considered relatively stable when compared to the moment-to-moment dynamic thoughts and feelings that are examined in inferential accuracy. Of the few studies of diagnostic competence that have examined more dynamic student states, the main focus has been on emotional experiences such as test anxiety or general feelings toward school (e.g., Zhu and Urhahne, 2021) and not on dynamic student mental states that change moment-to-moment within a lesson. Thus, inferential accuracy in the classroom could be viewed as a sub-construct of diagnostic competence that specifically examines teacher accuracy—one that occurs at a smaller grain-size than current measures employed to study diagnostic competence.
Teacher noticing
The second construct within teacher expertise that bears similarity to inferential accuracy (but also differs from it) is teacher noticing—how a teacher makes sense of the “noise” of a classroom and attends to (or ignores) information relevant to their proximal pedagogical goals (Sherin, 2014; Sherin et al., 2011). An expert teacher viewing a classroom mid-lesson is like a chess expert viewing a chessboard mid-game: they notice important features of the environment, ignore unimportant features, and extract meaningful patterns that novices miss, (e.g., an expert teacher may ignore some student misbehavior that does not jeopardize the flow of the lesson just as an expert chess player may ignore pieces that they have already blocked—see Chase and Simon, 1973).
When measuring both inferential accuracy and teacher noticing, attention is paid to how a perceiver (i.e., teacher) processes cues from the environment, but, as with diagnostic competence, inferential accuracy involves a somewhat smaller grain-size than prevalent current measures of teacher noticing. The study of teacher noticing has most often addressed the level of the classroom and focuses on how teachers extract cues of student learning and misbehavior from the class as a whole (Berliner, 2001; König et al., 2022). Inferential accuracy, on the other hand, occurs at the level of discrete student thoughts. This level may be more familiar in dyadic pedagogical interactions such as one-on-one tutoring, but many discretionary spaces within a full-class may be viewed as dyadic—for example, consider Ball's decision in our example to call the first student forward to share her thinking. Although Ball may have considered the other students in the class, that decision was based largely on her specific inference about that one student's thinking. One sub-facet of teacher noticing research, informal formative assessment (e.g., Sezen-Barrie and Kelly, 2017), bears a striking concordance with research findings about inferential accuracy that support using what a target says as a basis for accurate thought-feeling inferences. As such, we discuss informal formative assessment in more detail below.
Thus, inferential accuracy encompasses a dyadic exchange between teacher and student (differentiating it from the bulk of teacher noticing research) and touches on a mixture of dynamic socio-emotional and pedagogical states—at a grain-size that is finer than the relatively-stable traits that make up the bulk of diagnostic competence research. This is not to say that these areas of research cannot inform one another, but instead to specify that inferential accuracy embodies diagnostic competence and/or teacher noticing specifically within the micro-moments that are discretionary spaces.
We turn next to two widely studied educational constructs—pedagogical content knowledge and informal formative assessment—that have been used to understand teacher expertise and that we also believe play a role in inferential accuracy. Both of these educational constructs are themselves wide-reaching and heterogeneous (for a review of heterogeneity in pedagogical content knowledge, see Depaepe et al., 2013; for a review of heterogeneity within conceptualizations of informal formative assessment and teacher noticing, see König et al., 2022). Thus, in line with our goals for this conceptual review, we focus specifically on these constructs' possible connection to inferential accuracy.
Pedagogical content knowledge
Pedagogical content knowledge (PCK) is a manifest aspect of pedagogy that draws on teacher noticing and is the basis for real-time pedagogical decision-making (Ball, 1993; Ball et al., 2008; Ball and Bass, 2000; Kersting, 2008; König et al., 2022). PCK includes teachers' knowledge of pedagogy, the lesson material, their students, and how students generally learn the material, including the errors and misconceptions indicative of learning processes (Aliustaoglu and Tuna, 2021; Evens et al., 2015).
In line with one comprehensive model of PCK (i.e., the Refined Consensus Model of PCK; for a review, see Chan and Hume, 2019), we conceptualize PCK as existing on three levels and grain-sizes: collective, personal, and enacted PCK (for a review, see Behling et al., 2022). Collective PCK encompasses knowledge shared by multiple educators within a subject area and includes knowledge such as general misconceptions in student thinking (e.g., that the human body has only one blood stream; Behling et al., 2022). Research on collective PCK has included surveying content-area experts to map a subject-area (e.g., Vergara et al., 2024) and collective PCK may be cultivated within shared learning spaces such as reading groups (e.g., Cooper et al., 2022).
In contrast, personal PCK exists within a single teacher and is the individualized distillation of knowledge from collective PCK through that teacher's specific lens of experience, such as the cultural background of the teacher and of their students. Personal PCK can be articulated by the teacher outside of a pedagogical context, often in interviews or surveys (e.g., Aliustaoglu and Tuna, 2021). In the classroom case study we described earlier, Ball's personal PCK was demonstrated when she recruited a schema relevant to the lesson—specifically, that the disconnect between how the students had learned about fractions (as slices of pizza or pie) and number lines (as consisting only of whole numbers) made the task of labeling a fraction on a number line particularly difficult for students (Ball, 2018). Personal PCK shows a strong association with diagnostic competence (Kramer et al., 2021) and teacher noticing (Dreher and Kuntze, 2015). However, the variability of PCK operationalizations across subject area suggests that this relationship is largely defined within-study and should be considered in context (Alonzo et al., 2019; Vergara et al., 2024).
The third level of PCK, enacted PCK, differs from personal PCK in that it is contextualized within a particular pedagogical interaction with specific students: Enacted PCK only exists during teaching and is often difficult for teachers to recall and articulate (e.g., “Why did you use X metaphor to answer student Y's question?”—see Sherin et al., 2011). Because these moments occur frequently and are fleeting, they are often viewed as impossible to reason about post hoc (Behling et al., 2022). However, one method of peeling open teacher cognition underlying enacted PCK is by examining the relationship between a teacher's accuracy in inferring a student's thoughts during a discretionary space and their proximal enacted PCK, a method similar to the video-recorded lessons often used to study enacted PCK (e.g., Hoth et al., 2018, as well as methods used in inferential accuracy, see Hodges et al., 2015).
Inferential accuracy paradigms may be of particular interest to education researchers as an operationalization of enacted PCK. Although some studies have examined students' post-lesson understanding or quiz scores as correlates of PCK (e.g., Ali et al., 2020), we have not identified any that specifically measured the relationship between a teacher's accuracy in monitoring their students' thoughts during a lesson and their PCK. Within Ball's (2018) case study, the first student's explanation was interrupted by a second student who asked, “why'd you choose seven-eighths?” Ball's decision in this discretionary space to not reprimand the second student for interrupting but instead to allow the first student to respond with her mathematical reasoning reflected Ball's enacted PCK and was based on inferring that the student was demonstrating mathematical curiosity. This constituted an accurate inference made by an expert teacher who was familiar with the class. The variability of teacher responses between novice and expert teachers in moments like these may shed light on how enacted PCK is updated or adjusted during instruction. It may show where inaccuracy is not important (i.e., where the classroom script is sufficient) but also circumstances where inaccuracy may be particularly problematic for enacted PCK.
Informal formative assessment
We now turn to a second educational construct that intersects with inferential accuracy. Formative assessment encompasses the process by which teachers assess their students' understanding of lesson material (Bennett, 2011). Formative assessment is comprised of both formal formative assessment, which includes preplanned, graded demonstrations of student learning such as quizzes, tests, and class projects (Ayala et al., 2008; Black and Wiliam, 1998), and informal formative assessment (Ruiz-Primo, 2011), the unplanned and ungraded instances wherein teachers (or other students) encourage students to share their current thinking about the lesson material. We focus on informal formative assessment as an enterprise that draws on inferential accuracy in the classroom.
There are many different conceptualizations of informal formative assessment (IFA) and no strong consensus on a single definition or operationalization (König et al., 2022). Given this heterogeneity, we have chosen to frame our discussion in this section around one commonly-used model of IFA identified by Ruiz-Primo and Furtak (2007)—the “ESRU” cycle. Ruiz-Primo and Furtak describe an “ESRU” cycle thus: the teacher Elicits a response from a student on an aspect of the current lesson, the Student responds, and the teacher Recognizes the response, Utilizing the information to inform further cycles of instructional dialogue or to progress through the next portion of the lesson. ESRU cycles are an empirically supported teaching strategy (Leenknecht et al., 2021) for gathering data about a student's level of understanding (a pedagogically-related internal state). These instances often include evaluation from the teacher (e.g., acknowledging that the student correctly understands the material) and/or follow-up to further probe student understanding.
While PCK can be drawn upon to increase teachers' inferential accuracy, IFA within ESRU cycles intersects with inferential accuracy in a different way—as a means of directly eliciting information about students' thoughts. Of course, collecting information about a student's thinking is not the sole purpose of ESRU cycles; asking a student to articulate their thinking is itself a useful pedagogical tool both to reinforce that student's understanding as well as to provide opportunities for students to engage with the ideas of their peers (Tao and Chen, 2024). However, ESRU cycles may bolster instructors' inferential accuracy in two ways: first, by prompting students to directly tell teachers what they are thinking about lesson material; and second, by using ESRU cycles to elicit information that instructors can use to construct and update their inferences about what students are thinking and feeling (and potentially also their general PCK).
In Ball's (2018) case study, she made the first student's thinking explicit at two points during the interaction. First, Ball called on this student to share her initial answer. Ball leveraged her personal PCK to infer why the student made this choice and then Ball again made the student's thinking explicit by asking the student to articulate her reasoning to the class. This sequence differs from most inferential accuracy research, which collects retrospective inferences at either arbitrary intervals or those determined by the target while watching a video-taped social interaction (see Tipsord, 2009, for a rare measure of inferential accuracy driven by the perceiver). In contrast, the timing of Ball's attempts to uncover what the student was thinking used an ESRU cycle as a real-time strategy to facilitate inferential accuracy.
It is important to note that ESRU cycles may not yield entirely accurate information from students about what they are thinking. This may be especially true for non-specific or poorly implemented ESRU cycles (e.g., asking students, “do you get it?”). There are a myriad of social pressures influencing student responses that teachers must consider when assessing the veracity of students' self-reported understanding (for a discussion of how perceptions of possible target dishonesty affect inferential accuracy, see DesJardins and Hodges, 2015). For example, within the context of a math class, a student who experiences math anxiety (Ashcraft, 2002), low belongingness in math (Banchefsky et al., 2019; Good et al., 2012; Lewis and Hodges, 2015), math-related stereotype threat (Spencer et al., 1999), or a combination of the three may seek to conceal a low level of understanding (or perceived low-level of understanding) when responding to a teacher's question, preferring to say, “I don't know” rather than risk the embarrassment of being incorrect. Although classrooms are highly variable, examining teachers' ability to accurately infer students' true state of mind in these contexts may prove a productive path for future researchers.
Discussion: integrating inferential accuracy into classroom interactions and future questions
Our consideration of inferential accuracy in the context of educational research has likened it to a highly specific form of diagnostic competence and teacher noticing found at the underexamined grain-size level of student thoughts and feelings that may inform teacher choices in discretionary spaces. Prior research has examined teacher cognition during instruction, noting how teachers notice student learning, adapt to challenges, provide scaffolding on the fly, and flexibly support students during instruction (Klug et al., 2016; König et al., 2022; Loibl et al., 2020; Sasse et al., 2025). However, student thoughts and feelings—the unit of analysis examined in inferential accuracy—has received little-to-no attention, with research on teachers' expertise instead focused on post-lesson measures of student learning as the primary outcome measure (Tao and Chen, 2024). However, it is clear in Ball's (2018) case study that how teachers navigate discretionary spaces may also reflect expertise and one method of capturing this skill would be to examine inferential accuracy. Ball's example illustrates something we have aimed to do throughout this paper—that is, to make visible the connections between actions occurring in educational contexts that correspond to predictors of inferential accuracy. In the discussion that follows, we first consider sources of tension when bringing inferential accuracy research into the classroom before next turning to promising future directions where education and social psychology might fruitfully collaborate on inferential accuracy research.
Tension between inferential accuracy and education
Adapting inferential accuracy research to classroom contexts presents some challenges, although aspects of inferential accuracy paradigms are not entirely novel or foreign in studies of classroom interactions. Videos of classroom teaching are frequently used as stimuli when studying both PCK (Berliner, 2001; Hoth et al., 2018; Kersting, 2008; Kersting et al., 2016; van Es and Sherin, 2021) and IFA (Furtak et al., 2017; Gotwals et al., 2015; Sato et al., 2008; Wells and Arauz, 2006). However, inferential accuracy research differs from the modal study of these other topics in that it collects separate data from the perceiver (teacher) and the target (student). A point of difficulty may be the added vector of where students are developmentally and cognitively (e.g., Tucker-Drob, 2009). High variability in classroom teaching goals and content across grade level suggests that the relationship between inferential accuracy and instruction is likely to be very different across classroom contexts: A university lecturer may speak to a room of 300 students from a lectern 15 feet away from the first row of seats, whereas a teacher in a preschool class may never be more than 15 feet away from any of their 20 students. The importance of individual students' thoughts and feelings, the teacher's individualized knowledge of each student, and pedagogical goals in different classrooms may greatly affect how inferential accuracy relates to the teacher's instruction.
A cautionary note is in order: expecting past inferential accuracy findings based on data collected from dyads in controlled laboratory settings to generalize neatly to classroom settings is probably unreasonable. Researchers may find success in studying inferential accuracy in pedagogical dyads, but the mechanisms and processes underlying inferring the thoughts and feelings for one target may not generalize to the challenge of integrating or generalizing inferences across a whole classroom of students. The degree to which individual discretionary spaces are dyadic and thus amenable to examination is an empirical one. However, when viewing teacher decision-making at the grain-size of discretionary spaces, dyadic interactions may turn out to play an important role.
Future directions
In this paper, we have tried to lay the groundwork for potential collaboration between social psychology and education around inferential accuracy. Although we believe there are many possible avenues for such collaboration, we now highlight three future directions that may prove particularly fruitful. First, inferential accuracy may aid in distinguishing between the respective contributions of positive teacher-student relationships (e.g., Li et al., 2022) and content area expertise (e.g., Park and Chen, 2012). For example, to what extent is teacher expertise a function of how well a teacher knows their specific students, and does the variance in teacher expertise that is attributable to inferential accuracy help us to know how well teacher expertise may generalize across different subject areas? A math teacher's accuracy at inferring the thoughts and feelings of a familiar student learning material outside the teacher's usual content area (e.g., in a science class) may differ from the inferential accuracy of a science teacher encountering that same student for the first time in a science class. Although prior research on diagnostic competence and teacher noticing would give the advantage to the content-area expert (i.e., the science teacher—see Sherin et al., 2011) due to accuracy at inferring student thoughts germane to the lesson, there may also be a benefit conferred from accuracy at inferring thoughts irrelevant to the current lesson material, as this accuracy may contribute to positive teacher-student relationships (Yu et al., 2018).
Second, the study of inferential accuracy in the classroom may also open up new lines of research on how student readability affects instructional and learning success: Some students may be an “open book” to all their teachers, while others' minds may not be easily inferred or may vary in how readable they are based on the teacher or subject area (Lewis, 2014). By comparing student targets across different instructors and subject areas, researchers may find insights into how constructs like test anxiety or stereotype threat may vary in terms of how they impact student readability. For example, is one student highly readable in all their classes except math, where they feel considerable stereotype threat? Is another student an “open book” in class with their favorite instructor, but inscrutable elsewhere? Or perhaps student readability is generally stable across classroom instructor and subject area.
Third, social psychology's study of inferential accuracy research may have a great deal to gain from venturing into instructional settings, including developments in how inferential accuracy is studied and a better understanding of what can improve inferential accuracy. If any group should be proficient at inferring a student's thoughts and feelings during a lesson, it is likely to be teachers. It may be that teachers' PCK and expert schemas for student learning help teachers to make accurate inferences, or it may be that teachers' explicit requests for students to report what they are thinking as part of informal formative assessment provide teachers with better information. These strategies may be adapted to other contexts where people in certain roles need to know what targets are thinking and feeling. There may also be characteristics associated with teachers that help with inferential accuracy, e.g., factors related to self-selection in choosing teaching as a profession and/or a high motivation to accurately infer what students are thinking in order to help students or to succeed at teaching (higher motivation in certain contexts has been previously linked to greater inferential accuracy—see Klein and Hodges, 2001; Thomas and Maio, 2008). Additionally, classroom settings may broaden how inferential accuracy is defined and studied. For example, the skills and knowledge of expert teachers may entail monitoring many students simultaneously, and this ability may offer novel insights that may generalize to other, non-pedagogical contexts in which interactions involve more than a single dyad.
In closing, we have attempted to link research findings from the inferential accuracy literature with teacher practices in educational contexts and to draw connections between predictors of inferential accuracy and several common educational constructs (PCK, IFA). We have pointed out major sources of tension in trying to make these links, such as the difficulty in translating the dyadic methods (a pair of people interacting) that inferential accuracy research has primarily focused on into the classroom, where a teacher is interacting with multiple students. We have described areas of promising future research—some of them directly motivated by the interdisciplinary challenges of merging social psychological approaches in educational contexts. We expect that examining inferential accuracy in educational settings will involve some of the lines of inquiry we have explored here (e.g., PCK, IFA) and likely several others. Classrooms are complex social ecosystems in which teachers engage in specialized social cognition and leverage a diverse skillset to teach effectively. This complexity has resulted in a substantial body of research directed at understanding and improving teacher expertise—research that both may be further informed by incorporating insights from work on inferential accuracy and also may generate important new questions and answers about inferential accuracy.
Author contributions
ZS: Conceptualization, Writing – original draft, Writing – review & editing. JH: Conceptualization, Supervision, Writing – review & editing. SH: Conceptualization, Supervision, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. Preliminary work on this project began while Zachary J. Schroeder was supported by a U.S. National Science Foundation Graduate Research Fellowship (NSF GRFP Grant 2236419). Publication fees for this article were funded with awards from the University of Oregon Open Access Article Processing Charge Fund and from the University of Oregon Department of Psychology's Graduate Education Committee.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^In this paper, we use “dyad” to represent a student-teacher pair with teacher as perceiver and student as target. As we will discuss later, dyadic interactions may occur in full classrooms as long as they predominantly occur between one student and one teacher.
2. ^The formal social psychological definition of a stereotype is a generalization about members of a group (e.g., Aronson et al., 2010)—these generalizations may or may not be accurate. A correct generalization about members of a group (e.g., new mothers are generally tired) would be an accurate stereotype. However, to avoid negative connotations with prejudice and discrimination that are evoked by the use of the word stereotype, we use the term “schema” (which refers to a broad range cognitive constructs that scaffold people's perceptions, including stereotypes) in the current paper.
References
Ali, Z., Busch, M., Muhammad, N., Qaisrani, H., Hidayat, U., and Rehman, H. U. (2020). The influence of teachers' professional competencies on students' achievement: a quantitative research study. Am. Res. J. Humanit. Soc. Sci. 3, 45–54. doi: 10.54183/jssr.v3i2.272
Aliustaoglu, F., and Tuna, A. (2021). Examining the pedagogical content knowledge of prospective mathematics teachers on the subject of limits. Int. J. Math. Educ. Sci. Technol. 52, 833–856. doi: 10.1080/0020739X.2019.1703148
Alonzo, A. C., Berry, A., and Nilsson, P. (2019). “Unpacking the complexity of science teachers' PCK in action: enacted and personal PCK,” in Repositioning Pedagogical Content Knowledge in Teachers' Knowledge for Teaching Science, Eds. A. Hume, R. Cooper, and A. Borowski (Singapore: Springer Nature) 273–288.
Anderson, J., and Taner, G. (2023). Building the expert teacher prototype: a metasummary of teacher expertise studies in primary and secondary education. Educ. Res. Rev. 38:100485. doi: 10.1016/j.edurev.2022.100485
Aronson, E., Wilson, T. D., and Akert, R. M. (2010). Social Psychology, 7th Edn. Upper Saddle River, NJ: Pearson.
Ashcraft, M. H. (2002). Math anxiety: personal, educational, and cognitive consequences. Curr. Dir. Psychol. Sci. 11, 181–185. doi: 10.1111/1467-8721.00196
Ayala, C. C., Shavelson, R. J., Araceli Ruiz-Primo, M., Brandon, P. R., Yin, Y., Furtak, E. M., et al. (2008). From formal embedded assessments to reflective lessons: the development of formative assessment studies. Appl. Meas. Educ. 21, 315–334. doi: 10.1080/08957340802347787
Ball, D. L. (1993). With an eye on the mathematical horizon: dilemmas of teaching elementary school mathematics. Elem. Sch. J. 93, 373–397. doi: 10.1086/461730
Ball, D. L. (2018). Just Dreams and Imperatives: The Power of Teaching in the Struggle for Public Education. Presidential Address at the American Educational Research Association Annual Meeting, New York, NY. Available online at: https://youtu.be/JGzQ7O_SIYY (Accessed October 23, 2025).
Ball, D. L., and Bass, H. (2000). “Interweaving content and pedagogy in teaching and learning to teach: knowing and using mathematics,” in Multiple Perspectives on the Teaching and Learning of Mathematics, Ed. J. Boaler (Westport, CT: Ablex) 83–104.
Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content knowledge for teaching: what makes it special? J. Teach. Educ. 59, 389–407. doi: 10.1177/0022487108324554
Banchefsky, S., Lewis, K. L., and Ito, T. A. (2019). The role of social and ability belonging in men's and women's pSTEM persistence. Front. Psychol. 10:2386. doi: 10.3389/fpsyg.2019.02386
Behling, F., Förtsch, C., and Neuhaus, B. J. (2022). The refined consensus model of pedagogical content knowledge (PCK): detecting filters between the realms of PCK. Educ. Sci. 12:592. doi: 10.3390/educsci12090592
Bennett, R. E. (2011). Formative assessment: a critical review. Assess. Educ. Princ. Policy Pract. 18, 5–25. doi: 10.1080/0969594X.2010.513678
Berliner, D. (2001). Learning about and learning from expert teachers. Int. J. Educ. Res. 35, 463–482. doi: 10.1016/S0883-0355(02)00004-6
Beswick, J. F., Willms, J. D., and Sloat, E. A. (2005). A comparative study of teacher ratings of emergent literacy skills and student performance on a standardized measure. Education 126, 116–137.
Bhowmik, C. V., Back, M. D., Nestler, S., and Schrader, F.-W. (2025). Appearing smart, confident and motivated: a lens model approach to judgment accuracy in an educational setting. Soc. Psychol. Educ. 28, 105–134. doi: 10.1007/s11218-025-10057-1
Black, P., and Wiliam, D. (1998). Assessment and classroom learning. Assess. Educ. Princ. Policy Pract. 5, 7–74. doi: 10.1080/0969595980050102
Borko, H., Roberts, S. A., and Shavelson, R. (2008). “Teachers' decision making: from Alan J. Bishop to today,” in Critical Issues in Mathematics Education, Eds. P. Clarkson and N. Presmeg (Boston, MA: Springer US) 37–67.
Bromme, R. (2001). “Teacher expertise,” in International Encyclopedia of the Social & Behavioral Sciences, Vol. 22, Eds. N. Smelser and P. Baltes (Amsterdam: Elsevier), 15459–15465.
Chan, K. K. H., and Hume, A. (2019). “Towards a consensus model: literature review of how science teachers' pedagogical content knowledge is investigated in empirical studies,” in Repositioning Pedagogical Content Knowledge in Teachers' Knowledge for Teaching Science, Eds. A. Hume, R. Cooper, and A. Borowski (Singapore: Springer), 3–76.
Chase, W. G., and Simon, H. A. (1973). Perception in chess. Cogn. Psychol. 4, 55–81. doi: 10.1016/0010-0285(73)90004-2
Clarke, D., Clarke, B., and Roche, A. (2011). Building teachers' expertise in understanding, assessing and developing children's mathematical thinking: the power of task-based, one-to-one assessment interviews. ZDM Math. Educ. 43, 901–913. doi: 10.1007/s11858-011-0345-2
Cooper, R., Fitzgerald, A., and Carpendale, J. (2022). A reading group for science educators: an approach for developing personal and collective pedagogical content knowledge in science education. Int. J. Sci. Math. Educ. 20, 117–139. doi: 10.1007/s10763-022-10260-y
Demaray, M. K., and Elliot, S. N. (1998). Teachers' judgments of students' academic functioning: a comparison of actual and predicted performances. Sch. Psychol. Q. 13, 8–24. doi: 10.1037/h0088969
Depaepe, F., Verschaffel, L., and Kelchtermans, G. (2013). Pedagogical content knowledge: a systematic review of the way in which the concept has pervaded mathematics educational research. Teach. Teach. Educ. 34, 12–25. doi: 10.1016/j.tate.2013.03.001
DesJardins, N. M. L., and Hodges, S. D. (2015). Reading between the lies: empathic accuracy and deception detection. Soc. Psychol. Personal. Sci. 6, 781–787. doi: 10.1177/1948550615585829
Donker, M., van Aken, S., and Mainhard, T. (2023). “Using heart rate to tap into motivational and emotional processes during teaching and learning,” in Motivation and Emotion in Learning and Teaching across Educational Contexts, Eds. G. Hagenauer, R. Lazarides, and H. Järvenoja (London: Routledge).
Dreher, A., and Kuntze, S. (2015). Teachers' professional knowledge and noticing: the case of multiple representations in the mathematics classroom. Educ. Stud. Math. 88, 89–114. doi: 10.1007/s10649-014-9577-8
Eraut, M. (2007). Learning from other people in the workplace. Oxford Rev. Educ. 33, 403–422. doi: 10.1080/03054980701425706
Evens, M., Elen, J., and Depaepe, F. (2015). Developing pedagogical content knowledge: lessons learned from intervention studies. Educ. Res. Int. 2015:790417. doi: 10.1155/2015/790417
Furtak, E. M., Ruiz-Primo, M. A., and Bakeman, R. (2017). Exploring the utility of sequential analysis in studying informal formative assessment practices. Educ. Meas. Issues Pract. 36, 28–38. doi: 10.1111/emip.12143
Gesn, P. R., and Ickes, W. (1999). The development of meaning contexts for empathic accuracy: channel and sequence effects. J. Pers. Soc. Psychol. 77, 746–761. doi: 10.1037/0022-3514.77.4.746
Gleason, K. A., Jensen-Campbell, L. A., and Ickes, W. (2009). The role of empathic accuracy in adolescents' peer relations and adjustment. Pers. Soc. Psychol. Bull. 35, 997–1011. doi: 10.1177/0146167209336605
Good, C., Rattan, A., and Dweck, C. S. (2012). Why do women opt out? Sense of belonging and women's representation in mathematics. J. Pers. Soc. Psychol. 102, 700–717. doi: 10.1037/a0026659
Gotwals, A. W., Philhower, J., Cisterna, D., and Bennett, S. (2015). Using video to examine formative assessment practices as measures of expertise for mathematics and science teachers. Int. J. Sci. Math. Educ. 13, 405–423. doi: 10.1007/s10763-015-9623-8
Hall, J. A., and Schmid Mast, M. (2007). Sources of accuracy in the empathic accuracy paradigm. Emotion 7, 438–446. doi: 10.1037/1528-3542.7.2.438
Hattie, J. (2009). Visible Learning: A Synthesis of Over 800 Meta-Analyses Relating to Achievement. London: Routledge.
Heitzmann, N., Seidel, T., Hetmanek, A., Wecker, C., Fischer, M. R., Ufer, S., et al. (2019). Facilitating diagnostic competences in simulations in higher education: a framework and a research agenda. Frontline Learn. Res. 7, 1–24. doi: 10.14786/flr.v7i4.384
Helmke, A., and Schrader, F.-W. (1987). Interactional effects of instructional quality and teacher judgement accuracy on achievement. Teach. Teach. Educ. 3, 91–98. doi: 10.1016/0742-051X(87)90010-2
Hodges, S. D., and Kezer, M. (2021). It is hard to read minds without words: cues to use to achieve empathic accuracy. J. Intell. 9:27. doi: 10.3390/jintelligence9020027
Hodges, S. D., Kezer, M., Hall, J. A., and Vorauer, J. D. (2024). Exploring actual and presumed links between accurately inferring contents of other people's minds and prosocial outcomes. J. Intell. 12:13. doi: 10.3390/jintelligence12020013
Hodges, S. D., Lewis, K. L., and Ickes, W. (2015). “The matter of other minds: empathic accuracy and the factors that influence it,” in APA Handbook of Personality and Social Psychology, Volume 3: Interpersonal Relations, Eds. M. Mikulincer, P. R. Shaver, J. A. Simpson, and J. F. Dovidio (Washington, DC: American Psychological Association) 319–348.
Hoth, J., Kaiser, G., Döhrmann, M., König, J., and Blömeke, S. (2018). “A situated approach to assess teachers' professional competencies using classroom videos,” in Mathematics Teachers Engaging With Representations of Practice, Eds. O. Buchbinder and S. Kuntze (Cham: Springer International Publishing) 23–45.
Human, L. J., and Biesanz, J. C. (2013). Targeting the good target: an integrative review of the characteristics and consequences of being accurately perceived. Pers. Soc. Psychol. Rev. 17, 248–272. doi: 10.1177/1088868313495593
Ickes, W. (2016). “Empathic accuracy: judging thoughts and feelings,” in The Social Psychology of Perceiving Others Accurately, Eds. J. A. Hall, M. Schmid Mast, and T. V. West (Cambridge: Cambridge University Press) 52–70.
Ickes, W., Stinson, L., Bissonnette, V., and Garcia, S. (1990). Naturalistic social cognition: empathic accuracy in mixed-sex dyads. J. Pers. Soc. Psychol. 59, 730–742. doi: 10.1037/0022-3514.59.4.730
Jacobs, V. R., Lamb, L. L. C., and Philipp, R. A. (2010). Professional noticing of children's mathematical thinking. J. Res. Math. Educ. 41, 169–202. doi: 10.5951/jresematheduc.41.2.0169
Kersting, N. (2008). Using video clips of mathematics classroom instruction as item prompts to measure teachers' knowledge of teaching mathematics. Educ. Psychol. Meas. 68, 845–861. doi: 10.1177/0013164407313369
Kersting, N., Sutton, T., Kalinec-Craig, C., Stoehr, K. J., Heshmati, S., Lozano, G., et al. (2016). Further exploration of the classroom video analysis (CVA) instrument as a measure of usable knowledge for teaching mathematics: taking a knowledge system perspective. ZDM Math. Educ. 48, 97–109. doi: 10.1007/s11858-015-0733-0
Klassen, R. M., Perry, N. E., and Frenzel, A. C. (2012). Teachers' relatedness with students: an underemphasized component of teachers' basic psychological needs. J. Educ. Psychol. 104, 150–165. doi: 10.1037/a0026253
Klein, K. J. K., and Hodges, S. D. (2001). Gender differences, motivation, and empathic accuracy: when it pays to understand. Pers. Soc. Psychol. Bull. 27, 720–730. doi: 10.1177/0146167201276007
Klug, J., Bruder, S., and Schmitz, B. (2016). Which variables predict teachers' diagnostic competence when diagnosing students' learning behavior at different stages of a teacher's career? Teach. Teach. 22, 461–484. doi: 10.1080/13540602.2015.1082729
König, J., Santagata, R., Scheiner, T., Adleff, A.-K., Yang, X., and Kaiser, G. (2022). Teacher noticing: a systematic literature review of conceptualizations, research designs, and findings on learning to notice. Educ. Res. Rev. 36:100453. doi: 10.1016/j.edurev.2022.100453
Kramer, M., Förtsch, C., Boone, W. J., Seidel, T., and Neuhaus, B. J. (2021). Investigating pre-service biology teachers' diagnostic competences: relationships between professional knowledge, diagnostic activities, and diagnostic accuracy. Educ. Sci. 11:89. doi: 10.3390/educsci11030089
Kraus, M. W. (2017). Voice-only communication enhances empathic accuracy. Am. Psychol. 72, 644–654. doi: 10.1037/amp0000147
Leenknecht, M., Wijnia, L., Köhlen, M., Fryer, L., Rikers, R., and Loyens, S. (2021). Formative assessment as practice: the role of students' motivation. Assess. Eval. High. Educ. 46, 236–255. doi: 10.1080/02602938.2020.1765228
Lewis, K. L. (2014). Searching for the Open Book: Exploring Predictors of Target Readability in Interpersonal Accuracy (Ph.D. dissertation). University of Oregon, Eugene, OR. Available online at: https://hdl.handle.net/1794/18374 (Accessed October 23, 2025).
Lewis, K. L., and Hodges, S. D. (2015). Expanding the concept of belonging in academic domains: development and validation of the ability uncertainty scale. Learn. Individ. Differ. 37, 197–202. doi: 10.1016/j.lindif.2014.12.002
Lewis, K. L., Hodges, S. D., Laurent, S. M., Srivastava, S., and Biancarosa, G. (2012). Reading between the minds: the use of stereotypes in empathic accuracy. Psychol. Sci. 23, 1040–1046. doi: 10.1177/0956797612439719
Li, X., Bergin, C., and Olsen, A. A. (2022). Positive teacher-student relationships may lead to better teaching. Learn. Instr. 80:101581. doi: 10.1016/j.learninstruc.2022.101581
Loibl, K., Leuders, T., and Dörfler, T. (2020). A framework for explaining teachers' diagnostic judgements by cognitive modeling (DiaCoM). Teach. Teach. Educ. 91:103059. doi: 10.1016/j.tate.2020.103059
Machts, N., Kaiser, J., Schmidt, F. T. C., and Möller, J. (2016). Accuracy of teachers' judgments of students' cognitive abilities: a meta-analysis. Educ. Res. Rev. 19, 85–103. doi: 10.1016/j.edurev.2016.06.003
Marangoni, C., Garcia, S., Ickes, W., and Teng, G. (1995). Empathic accuracy in a clinically relevant setting. J. Pers. Soc. Psychol. 68, 854–869. doi: 10.1037/0022-3514.68.5.854
Meissel, K., Meyer, F., Yao, E. S., and Rubie-Davies, C. M. (2017). Subjectivity of teacher judgments: exploring student characteristics that influence teacher judgments of student ability. Teach. Teach. Educ. 65, 48–60. doi: 10.1016/j.tate.2017.02.021
Nickerson, R. S. (1999). How we know—and sometimes misjudge—what others know: imputing one's own knowledge to others. Psychol. Bull. 125, 737–759. doi: 10.1037/0033-2909.125.6.737
Palmer, D. J., Stough, L. M., Burdenski, T. K. Jr., and Gonzales, M. (2005). Identifying teacher expertise: an examination of researchers' decision making. Educ. Psychol. 40, 13–25. doi: 10.1207/s15326985ep4001_2
Park, S., and Chen, Y.-C. (2012). Mapping out the integration of the components of pedagogical content knowledge (PCK): examples from high school biology classrooms. J. Res. Sci. Teach. 49, 922–941. doi: 10.1002/tea.21022
Ropo, E. (2004). “Teaching expertise,” in Professional Learning: Gaps and Transitions on the Way from Novice to Expert, Eds. H. P. A. Boshuizen, R. Bromme, and H. Gruber (Dordrecht: Springer Netherlands) 159–179.
Ruiz-Primo, M. A. (2011). Informal formative assessment: the role of instructional dialogues in assessing students' learning. Stud. Educ. Eval. 37, 15–24. doi: 10.1016/j.stueduc.2011.04.003
Ruiz-Primo, M. A., and Furtak, E. M. (2007). Exploring teachers' informal formative assessment practices and students' understanding in the context of scientific inquiry. J. Res. Sci. Teach. 44, 57–84. doi: 10.1002/tea.20163
Sasse, H., Weber, A. M., Reuter, T., and Leuchter, M. (2025). Teacher guidance and on-the-fly scaffolding in primary school students' inquiry learning. Sci. Educ. 109, 579–604. doi: 10.1002/sce.21921
Sato, M., Wei, R. C., and Darling-Hammond, L. (2008). Improving teachers' assessment practices through professional development: the case of national board certification. Am. Educ. Res. J. 45, 669–700. doi: 10.3102/0002831208316955
Seidel, T., Schnitzler, K., Kosel, C., Stürmer, K., and Holzberger, D. (2021). Student characteristics in the eyes of teachers: differences between novice and expert teachers in judgment accuracy, observed behavioral cues, and gaze. Educ. Psychol. Rev. 33, 69–89. doi: 10.1007/s10648-020-09532-2
Sezen-Barrie, A., and Kelly, G. J. (2017). From the teacher's eyes: facilitating teachers noticings on informal formative assessments (IFAs) and exploring the challenges to effective implementation. Int. J. Sci. Educ. 39, 181–212. doi: 10.1080/09500693.2016.1274921
Sherin, M. G. (2014). “Developing a professional vision of classroom events,” in Beyond Classical Pedagogy: Teaching Elementary School Mathematics, Ed. T. D. Lampert (London: Taylor and Francis) 75–94.
Sherin, M. G., Jacobs, V. R., and Philipp, R. A. eds. (2011). Mathematics Teacher Noticing: Seeing Through Teachers' Eyes. New York, NY: Routledge.
Shulman, L. S. (2000). Teacher development: roles of domain expertise and pedagogical knowledge. J. Appl. Dev. Psychol. 21, 129–135. doi: 10.1016/S0193-3973(99)00057-X
Spencer, S. J., Steele, C. M., and Quinn, D. M. (1999). Stereotype threat and women's math performance. J. Exp. Soc. Psychol. 35, 4–28. doi: 10.1006/jesp.1998.1373
Stinson, L., and Ickes, W. (1992). Empathic accuracy in the interactions of male friends versus male strangers. J. Pers. Soc. Psychol. 62, 787–797. doi: 10.1037/0022-3514.62.5.787
Südkamp, A., Kaiser, J., and Möller, J. (2012). Accuracy of teachers' judgments of students' academic achievement: a meta-analysis. J. Educ. Psychol. 104, 743–762. doi: 10.1037/a0027627
Tao, Y., and Chen, G. (2024). The relationship between teacher talk and students' academic achievement: a meta-analysis. Educ. Res. Rev. 45:100638. doi: 10.1016/j.edurev.2024.100638
Thomas, G., and Maio, G. R. (2008). Man, I feel like a woman: when and how gender-role motivation helps mind-reading. J. Pers. Soc. Psychol. 95, 1165–1179. doi: 10.1037/a0013067
Tipsord, J. M. (2009). The Effects of Mindfulness Training and Individual Differences in Mindfulness on Social Perception and Empathy (Ph.D. dissertation). University of Oregon, Eugene, OR.
Tobin, K., King, D., Henderson, S., Bellocchi, A., and Ritchie, S. M. (2016). Expression of emotions and physiological changes during teaching. Cult. Stud. Sci. Educ. 11, 669–692. doi: 10.1007/s11422-016-9778-9
Tsui, A. B. M. (2005). “Expertise in teaching: perspectives and issues,” in Expertise in Second Language Learning and Teaching, Ed. K. Johnson (London: Palgrave Macmillan UK) 167–189.
Tsui, A. B. M. (2009). Distinctive qualities of expert teachers. Teach. Teach. Theory Pract. 15, 421–439. doi: 10.1080/13540600903057179
Tucker-Drob, E. M. (2009). Differentiation of cognitive abilities across the life span. Dev. Psychol. 45, 1097–1118. doi: 10.1037/a0015864
Urhahne, D., and Wijnia, L. (2021). A review on the accuracy of teacher judgments. Educ. Res. Rev. 32:100374. doi: 10.1016/j.edurev.2020.100374
van Dijk, E. E., van Tartwijk, J., van der Schaaf, M. F., and Kluijtmans, M. (2020). What makes an expert university teacher? A systematic review and synthesis of frameworks for teacher expertise in higher education. Educ. Res. Rev. 31:100365.
van Es, E. A., and Sherin, M. G. (2021). Expanding on prior conceptualizations of teacher noticing. ZDM Math. Educ. 53, 17–27. doi: 10.1007/s11858-020-01211-4
Vergara, C., Bassaber, A., Núñez Nieto, P., Becerra, B., Hurtado, H., Santibáñez, D., et al. (2024). A map of collective pedagogical content knowledge as a basis for studying the development of biology teachers' personal PCK of evolution. Int. J. Sci. Educ. 1–23. doi: 10.1080/09500693.2024.2381841
Wells, G., and Arauz, R. M. (2006). Dialogue in the classroom. J. Learn. Sci. 15, 379–428. doi: 10.1207/s15327809jls1503_3
Wettstein, A., Krähling, S., Jenni, G., Schneider, I., and Kühne, F. (2024). Teachers' heart rate variability and behavioral reactions in aggressive interactions: teachers can downregulate their physiological arousal, and progesterone favors social integrative teacher responses. Eur. J. Investig. Health Psychol. Educ. 14, 2230–2247. doi: 10.3390/ejihpe14080149
Wilson, M. (2024). Finding the right grain-size for measurement in the classroom. J. Educ. Behav. Stat. 49, 3–31. doi: 10.3102/10769986231159006
Yu, M. V. B., Johnson, H. E., Deutsch, N. L., and Varga, S. M. (2018). “She calls me by my last name”: exploring adolescent perceptions of positive teacher-student relationships. J. Adolesc. Res. 33, 332–362. doi: 10.1177/0743558416684958
Keywords: inferential accuracy, empathic accuracy, pedagogical content knowledge, informal formative assessment, discretionary spaces
Citation: Schroeder ZJ, Husman J and Hodges SD (2025) Inferential accuracy in classroom contexts. Front. Psychol. 16:1647219. doi: 10.3389/fpsyg.2025.1647219
Received: 15 June 2025; Accepted: 17 October 2025;
Published: 07 November 2025.
Edited by:
Eva Hammar Chiriac, Linköping University, SwedenReviewed by:
Andreas Rieu, University of Education Freiburg, GermanyMario Fernando Gutiérrez-Romero, Pontificia Universidad Javeriana, Colombia
Copyright © 2025 Schroeder, Husman and Hodges. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zachary J. Schroeder, enNjaHJvZTJAdW9yZWdvbi5lZHU=
 Zachary J. Schroeder
Zachary J. Schroeder Jenefer Husman
Jenefer Husman Sara D. Hodges
Sara D. Hodges