Directional Control of Rayleigh Wave Propagation in an Elastic Lattice by Gyroscopic Effects

1 Introduction

According to their original definition, Rayleigh waves are a class of elastic waves that propagate on the surface of an infinite homogenous isotropic solid, and they are confined within a superficial region whose thickness is comparable with their wavelength (Rayleigh, 1885). These waves are well known by seismologists, since they are usually detected after the occurrence of an earthquake. They are also observed in other common urban activities, such as construction and demolition works and vehicular traffic, in addition to industrial processes and technologies, like mining exploration, non-destructive testing and design of electronic instruments. In the literature, they have been studied in depth especially with reference to continuous media (see, for instance, the classical treatizes by Viktorov (1967), Achenbach (1973) and Graff (1975)).

Surface waves traveling on the free boundaries of periodic media are usually referred to as Rayleigh-Bloch waves. They are of great importance in problems concerning the dynamic propagation of cracks in discrete systems, as discussed by Marder and Gross (1995) and Slepyan (2002) for uniform media and in successive works (Nieves et al., 2013) for non-uniform lattices. Similar localized phenomena may play a substantial role in non-uniform crack propagation as evidenced in (Piccolroaz et al., 2020), where lattice dissimilarity has been shown to promote or diminish localized deformations around the faces of the crack. Trapped modes associated with Rayleigh-Bloch waves in systems incorporating periodic gratings or periodic arrays of resonators were analyzed by Porter and Evans (1999), Porter and Evans (2005), Linton and McIver (2002) and Antonakakis et al. (2014) for scalar problems, by Colquitt et al. (2015) for vector systems and by Haslinger et al. (2017) and Morvaridi et al. (2018) for plates.

Recently, there has been an increasing interest in the design and fabrication of elastic media with unusual properties, often referred to as metamaterials (see the recent works by Filipov et al. (2015), Misseroni et al. (2016), Armanini et al. (2017), Bordiga et al. (2018), Bacigalupo et al. (2019), Al Ba’ba’a et al. (2020), Tallarico et al. (2020) and Wenzel et al. (2020) amongst others). In this paper, we focus the attention on an elastic metamaterial consisting of a triangular lattice connected to a system of gyroscopic spinners. The presence of gyroscopic spinners breaks the time-reversal symmetry of the system and makes the medium non-reciprocal, as proved by Nieves et al. (2020). We observe that the gyroscopic effect plays the role of magnetic bias (Bi et al., 2011) or angular momentum (Sounas et al., 2013) in linear non-reciprocal electromagnetic metamaterials and of circulating fluids in acoustic linear circulators (Fleury et al., 2014).

Firstly introduced by Brun et al. (2012) and later developed by Carta et al. (2014), a gyroscopic elastic lattice is a tunable system, whose dispersive properties can be varied by changing the spin and precession rates of the spinners. This type of metamaterial can be utilized to force waves to propagate along a line, whose direction is defined by the geometry of the medium (Carta et al., 2017). Gyroscopic spinners can also be employed to design topological insulators, where waves travel in one direction and are immune to backscattering (Nash et al., 2015; Süsstrunk and Huber, 2015; Wang et al., 2015; Garau et al., 2018; Lee et al., 2018; Mitchell et al., 2018; Carta et al., 2019; Garau et al., 2019; Carta et al., 2020). Furthermore, systems with gyroscopic spinners can be used to design coatings to hide the presence of objects in a continuous or discrete medium (Brun et al., 2012; Garau et al., 2019). In a recent work by Nieves et al. (2020), the dispersion analysis of Rayleigh waves in a semi-infinite triangular gyroscopic lattice has been carried out. The non-symmetry of the eigenmodes of the lattice’s particles at the free boundary for positive and negative values of the wave number has been linked to the non-symmetry of the system’s response to an applied force, determined by means of finite element simulations. In addition, a comparison with an effective gyroscopic continuum discussed in that paper has corroborated the results for the discrete system when low values of the wave number are considered.

In this paper, we present for the first time the analytical derivation of the displacement field in a semi-infinite elastic lattice incorporating gyroscopic spinners, focusing the attention on Rayleigh waves. Conversely, the main objective of previous papers (Garau et al., 2018, 2019) was related to the study of topologically-protected waveforms in lattices incorporating sub-domains with different values of the parameters of the gyroscopic spinners. The analytical results of the present paper are also verified with an independent finite element code. The displacement field produced by a point load acting on the boundary of the medium and the calculation of the energy flow demonstrate that the considered system is non-reciprocal, as the response of the forced lattice is not symmetric with respect to the point of application of the concentrated load. The influence of different physical quantities on the behavior of the gyroscopic system is also investigated through a detailed parametric analysis.

While in (Nieves et al., 2020) the wave field produced by a force on the boundary was determined numerically by using a finite element code, here the response of the system is calculated by means of a novel analytical formulation. The latter has many advantages. First, it does not require Adaptive Absorbing Layers (AAL) to prevent wave reflections at the boundaries of the computational domain; in fact, AAL are frequency-dependent and, as a consequence, their characteristic parameters need to be tuned manually every time the frequency is changed. The analytical formulation does not require the introduction of fictitious boundaries as in finite element codes. Second, the analytical formulation allows one to perform a parametric analysis quickly and efficiently, a task that is not straightforward in many finite element packages and that is performed here. Third, analytical results are necessary to validate the outcomes of finite element models. For these reasons, it is envisaged that the proposed analytical approach can be useful to the interested reader to tackle similar dynamic problems in discrete elastic systems.

2 Materials and Methods

The material under consideration consists of a semi-infinite two-dimensional triangular lattice of masses m, linked by elastic springs of stiffness γ, length L and whose inertia is negligible in comparison with m. The planar and three-dimensional representations of the lattice are shown in Figures 1A,C, respectively. In addition, each mass is attached to a gyroscopic spinner (see Figure 1B), whose configuration is described by the Euler angles θ, ϕ and ψ, denoted as the nutation, precession and spin angles, respectively. We assume that the nutation angle θ is small ($\theta \ll 1$), together with the displacement of the mass attached to the spinner. Each gyroscopic spinner has length l, moments of inertia $I_1$ about the axis of revolution and $I_0$ about the other two principal axes passing through the spinner’s base. Firstly derived by Carta et al. (2018) and Nieves et al. (2018), the gyricity$\text{Ω}$ is an independent parameter, representing the sum of the initial precession and spin rates, that remains constant throughout the motion: $\text{Ω}=\dot{\varphi }+\dot{\psi }=\text{Const}$. We also introduce the effective gyricity${\text{Ω}}^{\text{*}}=\text{Ω}\left[I_1/\left(I_0+m{l}^2\right)\right]$ and the effective mass$m^{\text{*}}=m\left[1+I_0/\left(m{l}^2\right)\right]$, that both include the inertial contribution of the spinners.

FIGURE 1

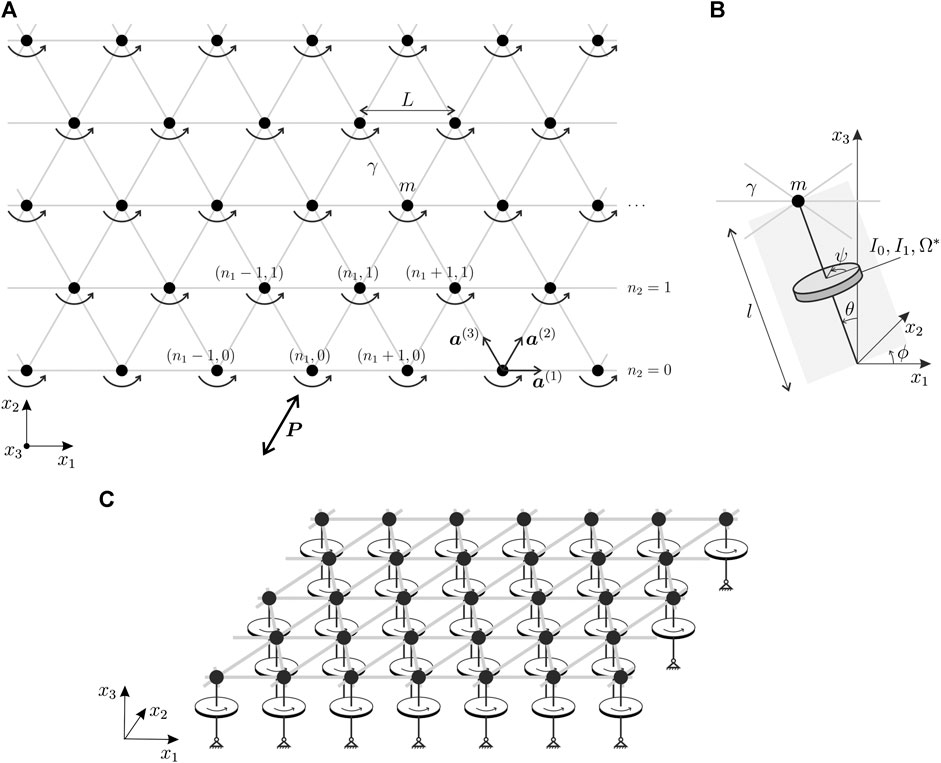
FIGURE 1. (A) Semi-infinite triangular array of masses, interconnected by elastic links and joined to gyroscopic spinners; a point force is applied on the boundary of the medium. (B) Representation of a gyroscopic spinner attached to a lattice’s mass; θ, ϕ and ψ indicate the nutation, precession and spin angles, respectively. (C) Three-dimensional sketch of the gyro-elastic lattice.

In practice, such a lattice can be realized by constructing a triangular array of masses (represented, for example, by spheres) connected by thin elastic rods. At the bottom part of each mass a cylindrical hole can be drilled, where the tip of the gyroscopic spinner can be inserted. The connection needs to be frictionless, so that the spinning motion of the gyroscope is not transmitted to the mass, which can only move in the x₁- or x₂‐direction without rotating. The spinning motion of the gyroscopic spinner can be applied by using an electric motor; in this way, its spin rate can remain constant during the motion. Each gyroscopic spinner is pinned at the base and its axis is parallel to the $x_3$‐direction in the initial configuration.

The boundary of the semi-infinite lattice is subjected to an oscillatory force of amplitude $\mathit{P}$ and prescribed radian frequency ${\omega }_0$ (see Figure 1A), which generates Rayleigh waves localized at the boundary and bulk waves propagating inside the medium. The displacement of a generic particle, whose position is identified by the multi-index $\mathbf{n}={\left(n_1,n_2\right)}^{\text{T}}$, is denoted by ${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)$ and is a function of time t.

We introduce the following normalizations:

$\begin{array}{l}\mathbf{x}=\tilde{\mathbf{x}}L,{\mathbf{u}}^{\left(n_1,n_2\right)}={\tilde{\mathbf{u}}}^{\left(n_1,n_2\right)}L,t=\tilde{t}\sqrt{m^{\text{*}}/\gamma },\\ {\omega }_0={\tilde{\omega }}_0\sqrt{\gamma /m^{\text{*}}},{\text{Ω}}^{\text{*}}={\widetilde{\text{Ω}}}^{\text{*}}\sqrt{\gamma /m^{\text{*}}},\mathbf{P}=\tilde{\mathbf{P}}\gamma L,\end{array}(1)$

where the tilde symbol indicates a dimensionless quantity. In the following, the tilde is omitted for ease of notation and it is assumed that all the appearing quantities are dimensionless.

2.1 Governing Equations of the Forced Lattice in the Transient Regime

The equations of motion of a mass within the bulk of the lattice are given in normalized form as (Garau et al., 2019)

$\begin{array}{l}{\ddot{\mathbf{u}}}^{\left(n_1,n_2\right)}=-{\text{Ω}}^{\text{*}}\mathbf{R}{\dot{\mathbf{u}}}^{\left(n_1,n_2\right)}+[{\mathbf{a}}^{\left(1\right)}\cdot \left({\mathbf{u}}^{\left(n_1+1,n_2\right)}+{\mathbf{u}}^{\left(n_1-1,n_2\right)}-2{\mathbf{u}}^{\left(n_1,n_2\right)}\right){\mathbf{a}}^{\left(1\right)}\\ \mathit{+}{\mathbf{a}}^{\left(2\right)}\cdot \left({\mathbf{u}}^{\left(n_1,n_2+1\right)}+{\mathbf{u}}^{\left(n_1,n_2-1\right)}-2{\mathbf{u}}^{\left(n_1,n_2\right)}\right){\mathbf{a}}^{\left(2\right)}\\ +{\mathbf{a}}^{\left(3\right)}\cdot \left({\mathbf{u}}^{\left(n_1-1,n_2+1\right)}+{\mathbf{u}}^{\left(n_1+1,n_2-1\right)}-2{\mathbf{u}}^{\left(n_1,n_2\right)}\right){\mathbf{a}}^{\left(3\right)}],n_1,n_2\in \mathrm{\mathbb{Z}},n_2>0,\end{array}(2)$

where

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)=\mathbf{u}\left(x_1,x_2,t\right),(3)$

with

$x_1=n_1+\frac{n_2}{2},x_2=\frac{\sqrt{3}{n}_2}{2}.(4)$

Further, the dot denotes the time derivative, the vectors ${\mathbf{a}}^{\left(i\right)}$ ($i=\mathrm{1,2,3}$) are

${\mathbf{a}}^{\left(1\right)}={\left(\mathrm{1,0}\right)}^{\text{T}},{\mathbf{a}}^{\left(2\right)}={\left(1/2,\sqrt{3}/2\right)}^{\text{T}},{\mathbf{a}}^{\left(3\right)}={\left(-1/2,\sqrt{3}/2\right)}^{\text{T}},(5)$

as shown in Figure 1A, and the matrix $\mathbf{R}$ is

$\mathbf{R}=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right).(6)$

The governing equations for a mass belonging to the boundary of the semi-infinite lattice ($n_2=0$) are

$\begin{array}{l}{\ddot{\mathbf{u}}}^{\left(n_1,0\right)}=-{\text{Ω}}^{\text{*}}\mathbf{R}{\dot{\mathbf{u}}}^{\left(n_1,0\right)}+[{\mathbf{a}}^{\left(1\right)}\cdot \left({\mathbf{u}}^{\left(n_1+\mathrm{1,0}\right)}+{\mathbf{u}}^{\left(n_1-\mathrm{1,0}\right)}-2{\mathbf{u}}^{\left(n_1,0\right)}\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left({\mathbf{u}}^{\left(n_1,1\right)}-{\mathbf{u}}^{\left(n_1,0\right)}\right){\mathbf{a}}^{\left(2\right)}+{\mathbf{a}}^{\left(3\right)}\cdot \left({\mathbf{u}}^{\left(n_1-\mathrm{1,1}\right)}-{\mathbf{u}}^{\left(n_1,0\right)}\right){\mathbf{a}}^{\left(3\right)}]\\ +\mathbf{P}\cos \left({\omega }_{0}t\right){\delta }_{n_1,0},n_1\in \mathrm{\mathbb{Z}},\end{array}(7)$

where

${\delta }_{i,j}=\{\begin{array}{cc}1,& i=j,\\ 0,& \text{otherwise},\end{array}(8)$

is the Kronecker delta.

In addition, we assume that the lattice is at rest initially, namely:

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(0\right)={\dot{\mathbf{u}}}^{\left(n_1,n_2\right)}\left(0\right)=0,n_1,n_2\in \mathrm{\mathbb{Z}},n_2\ge 0.(9)$

2.2 Alternative Representations of the Governing Equations in the Transient Regime

We introduce the integer $p=2n_1$ and the transient solution in the form

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)=\text{Re}\left({\mathbf{U}}^{\left(p,n_2\right)}\left(t\right)e^{\text{i}{\omega }_{0}t}\right),(10)$

where the time-dependent complex displacement amplitude ${\mathbf{U}}^{\left(p,n_2\right)}\left(t\right)=\mathbf{U}\left(p+n_2,n_2,t\right)$ satisfies the conditions of zero initial velocity and displacement. In addition, note that for $\alpha ,\beta \in \mathrm{\mathbb{Z}}$

${\mathbf{U}}^{\left(p,n_2\right)}\left(t\right){|}_{\begin{array}{c}{n}_1=n_1+\alpha \\ n_2=n_2+\beta \end{array}}={\mathbf{U}}^{\left(p+2\alpha +\beta ,n_2+\beta \right)}\left(t\right).(11)$

In terms of these complex displacement amplitudes, Eqs. 2,7 become:

$\begin{array}{l}-{\omega }_0^2{\mathbf{U}}^{\left(p,n_2\right)}+\left(2\text{i}{\omega }_0\mathbf{I}+{\text{Ω}}^{\text{*}}\mathbf{R}\right){\dot{\mathbf{U}}}^{\left(p,n_2\right)}+\text{i}{\omega }_0{\text{Ω}}^{\text{*}}\mathbf{R}{\mathbf{U}}^{\left(p,n_2\right)}+{\ddot{\mathbf{U}}}^{\left(p,n_2\right)}\\ =[{\mathbf{a}}^{\left(1\right)}\cdot \left({\mathbf{U}}^{\left(p+2,n_2\right)}+{\mathbf{U}}^{\left(p-2,n_2\right)}-2{\mathbf{U}}^{\left(p,n_2\right)}\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left({\mathbf{U}}^{\left(p+1,n_2+1\right)}+{\mathbf{U}}^{\left(p-1,n_2-1\right)}-2{\mathbf{U}}^{\left(p,n_2\right)}\right){\mathbf{a}}^{\left(2\right)}\\ +{\mathbf{a}}^{\left(3\right)}\cdot \left({\mathbf{U}}^{\left(p-1,n_2+1\right)}+{\mathbf{U}}^{\left(p+1,n_2-1\right)}-2{\mathbf{U}}^{\left(p,n_2\right)}\right){\mathbf{a}}^{\left(3\right)}],n_1,n_2\in \mathrm{\mathbb{Z}},n_2>0,\end{array}(12)$

and

$\begin{array}{l}-{\omega }_0^2{\mathbf{U}}^{\left(p,0\right)}+\left(2\text{i}{\omega }_0\mathbf{I}+{\text{Ω}}^{\text{*}}\mathbf{R}\right){\dot{\mathbf{U}}}^{\left(p,0\right)}+\text{i}{\omega }_0{\text{Ω}}^{\text{*}}\mathbf{R}{\mathbf{U}}^{\left(p,0\right)}+{\ddot{\mathbf{U}}}^{\left(p,0\right)}\\ =[{\mathbf{a}}^{\left(1\right)}\cdot \left({\mathbf{U}}^{\left(p+\mathrm{2,0}\right)}+{\mathbf{U}}^{\left(p-\mathrm{2,0}\right)}-2{\mathbf{U}}^{\left(p,0\right)}\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left({\mathbf{U}}^{\left(p+\mathrm{1,1}\right)}-{\mathbf{U}}^{\left(p,0\right)}\right){\mathbf{a}}^{\left(2\right)}\\ +{\mathbf{a}}^{\left(3\right)}\cdot \left({\mathbf{U}}^{\left(p-\mathrm{1,1}\right)}-{\mathbf{U}}^{\left(p,0\right)}\right){\mathbf{a}}^{\left(3\right)}]+\mathbf{P}{\delta }_{p,0},n_2=0,n_1\in \mathrm{\mathbb{Z}},\end{array}(13)$

where $\mathbf{I}$ is the identity matrix. In the last equation, the complex representation for the applied force was used.

2.2.1 Laplace and Fourier Transformed Equations for the Complex Displacement Amplitudes

Next, we apply the Laplace transform in time t to Eqs. 12,13 and we use the fact that the displacement amplitudes satisfy zero initial conditions. After this, we apply the discrete Fourier transform with respect to $n_1\in \mathrm{\mathbb{Z}}$$x_1$. In what follows, ${\mathbf{U}}_{n_2}^{\text{LF}}$ denotes the Laplace and discrete Fourier transform of the solution, defined as

${\mathbf{U}}_{n_2}^{\text{LF}}\left(s,k_1\right)={\displaystyle \sum _{n_1=-\infty }^{\infty }{\displaystyle {\int }_0^{\infty }{\mathbf{U}}^{\left(p,n_2\right)}\left(t\right)e^{-st+\text{i}{k}_1(n_1+n_2/2)}dt}}.(14)$

Here, s and $k_1$ are the Laplace and discrete Fourier transform parameters, respectively. The Fourier transform parameter $k_1$ will also be referred to as the (normalized) wave number.

For the equations in the bulk, we obtain that the complex displacement amplitude satisfies

$\begin{array}{l}\left[{\left(s+\text{i}{\omega }_0\right)}^2\mathbf{I}+{\text{Ω}}^{\text{*}}\left(s+\text{i}{\omega }_0\right)\mathbf{R}\right]{\mathbf{U}}_{n_2}^{\text{LF}}\left(s,k_1\right)=2{\mathbf{a}}^{\left(1\right)}\cdot \left(\text{cos}\left(k_1\right)-1\right){\mathbf{U}}_{n_2}^{\text{LF}}\left(s,k_1\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left(e^{-\text{i}{k}_1/2}{\mathbf{U}}_{n_2+1}^{\text{LF}}\left(s,k_1\right)+e^{\text{i}{k}_1/2}{\mathbf{U}}_{n_2-1}^{\text{LF}}\left(s,k_1\right)-2{\mathbf{U}}_{n_2}^{\text{LF}}\left(s,k_1\right)\right){\mathbf{a}}^{\left(2\right)}\\ +{\mathbf{a}}^{\left(3\right)}\cdot \left(e^{\text{i}{k}_1/2}{\mathbf{U}}_{n_2+1}^{\text{LF}}\left(s,k_1\right)+e^{-\text{i}{k}_1/2}{\mathbf{U}}_{n_2-1}^{\text{LF}}\left(s,k_1\right)-2{\mathbf{U}}_{n_2}^{\text{LF}}\left(s,k_1\right)\right){\mathbf{a}}^{\left(3\right)},\end{array}(15)$

for $n_2>0$, where the factor $e^{(-n^2/2)}$ appearing throughout due to the application of the discrete Fourier transform has been cancelled (see Eq. 10). Similar conversions for Eq. 7 describing the forced boundary at $n_2=0$ lead to

$\begin{array}{l}\left[{\left(s+\text{i}{\omega }_0\right)}^2\mathbf{I}+{\text{Ω}}^{\text{*}}\left(s+\text{i}{\omega }_0\right)\mathbf{R}\right]{\mathbf{U}}_0^{\text{LF}}\left(s,k_1\right)=\frac{1}{s}\mathbf{P}+2{\mathbf{a}}^{\left(1\right)}\cdot \left(\text{cos}\left(k_1\right)-1\right){\mathbf{U}}_0^{\text{LF}}\left(s,k_1\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left(e^{-\text{i}{k}_1/2}{\mathbf{U}}_1^{\text{LF}}\left(s,k_1\right)-{\mathbf{U}}_0^{\text{LF}}\left(s,k_1\right)\right){\mathbf{a}}^{\left(2\right)}+{\mathbf{a}}^{\left(3\right)}\cdot \left(e^{\text{i}{k}_1/2}{\mathbf{U}}_1^{\text{LF}}\left(s,k_1\right)-{\mathbf{U}}_0^{\text{LF}}\left(s,k_1\right)\right){\mathbf{a}}^{\left(3\right)}.\end{array}(16)$

2.3 Analysis of the Forced Problem in the Steady-State Regime

The transition to the steady-state regime (i.e. when $t\to +\infty$) is made by multiplying Eqs. 15,16 by the Laplace transform parameter s and taking the limit as $s\to +0$. In this limit, we define the discrete Fourier transform of the displacement amplitude in the steady-state regime as

${\mathbf{U}}_{n_2}^{\text{F}}\left(k_1\right)=\underset{s\to +0}{\text{lim}}s{\mathbf{U}}_{n_2}^{\text{LF}}\left(s,k_1\right),n_2\in \mathrm{\mathbb{Z}},n_2\ge 0.(17)$

From Eqs. 15,16, these transformed amplitudes then satisfy

$\begin{array}{l}\left[-{\left({\omega }_0-\text{i}0\right)}^2\mathbf{I}+{\text{iΩ}}^{\text{*}}\left({\omega }_0-\text{i}0\right)\mathbf{R}\right]{\mathbf{U}}_{n_2}^{\text{F}}\left(k_1\right)=2{\mathbf{a}}^{\left(1\right)}\cdot \left(\text{cos}\left(k_1\right)-1\right){\mathbf{U}}_{n_2}^{\text{F}}\left(k_1\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left(e^{-\text{i}{k}_1/2}{\mathbf{U}}_{n_2+1}^{\text{F}}\left(k_1\right)+e^{\text{i}{k}_1/2}{\mathbf{U}}_{n_2-1}^{\text{F}}\left(k_1\right)-2{\mathbf{U}}_{n_2}^{\text{F}}\left(k_1\right)\right){\mathbf{a}}^{\left(2\right)}\\ +{\mathbf{a}}^{\left(3\right)}\cdot \left(e^{\text{i}{k}_1/2}{\mathbf{U}}_{n_2+1}^{\text{F}}\left(k_1\right)+e^{-\text{i}{k}_1/2}{\mathbf{U}}_{n_2-1}^{\text{F}}\left(k_1\right)-2{\mathbf{U}}_{n_2}^{\text{F}}\left(k_1\right)\right){\mathbf{a}}^{\left(3\right)},\end{array}(18)$

for $n_2>0$ and

$\begin{array}{l}\left[-{\left({\omega }_0-\text{i}0\right)}^2\mathbf{I}+{\text{iΩ}}^{\text{*}}\left({\omega }_0-\text{i}0\right)\mathbf{R}\right]{\mathbf{U}}_0^{\text{F}}\left(k_1\right)=\mathbf{P}+2{\mathbf{a}}^{\left(1\right)}\cdot \left(\text{cos}\left(k_1\right)-1\right){\mathbf{U}}_0^{\text{F}}\left(k_1\right){\mathbf{a}}^{\left(1\right)}\\ +{\mathbf{a}}^{\left(2\right)}\cdot \left(e^{-\text{i}{k}_1/2}{\mathbf{U}}_1^{\text{F}}\left(k_1\right)-{\mathbf{U}}_0^{\text{F}}\left(k_1\right)\right){\mathbf{a}}^{\left(2\right)}+{\mathbf{a}}^{\left(3\right)}\cdot \left(e^{\text{i}{k}_1/2}{\mathbf{U}}_1^{\text{F}}\left(k_1\right)-{\mathbf{U}}_0^{\text{F}}\left(k_1\right)\right){\mathbf{a}}^{\left(3\right)},\end{array}(19)$

for $n_2=0$. Here, ${\omega }_0-\text{i}0={\text{lim}}_{s\to +0}\left({\omega }_0-\text{i}s\right)$, and in what follows “$\text{i}0$” will represent a small imaginary term with positive imaginary part. The presence of this term enables one to determine how singular points of the Fourier transformed solution approach the real axis in the complex plane in passing to the steady-state regime. In this limit, the location of these singular points in the complex plane provides a way of ascertaining the direction of waves propagating in the medium relative to the load position. This is linked to the causality principle (see Section 3.3.2 in (Slepyan, 2002) for more details).

2.4 Solution to the Transformed Steady-State Forced Problem

The transformed amplitudes ${\mathbf{U}}_{n_2}^{\text{F}}$ are sought in the form

${\mathbf{U}}_{n_2}^{\text{F}}=\mathbf{U}{\text{Λ}}^{n_2}.(20)$

Here, $\text{Λ}$ is such that $\left|\text{Λ}\right|<1$ for $n_2\ge 1$, since we are considering waves that decay into the bulk of the lattice.

The solution in Eq. 20 is inserted into Eq. 18 in order to find the eigensolutions for waves in the bulk; using Eq. 19 it is then possible to satisfy conditions at $n_2=0$ and find the response to the applied load. The full derivation is reported in the Supplementary Material, where it is shown that the solution has the form

${\mathbf{U}}_{n_2}^{\text{F}}={\mathbf{U}}_0{\mathbf{\Lambda }}^{n_2}{\left[{\mathbf{M}}_2\right]}^{-1}{\mathbf{P}|}_{{\omega }_0={\omega }_0-\text{i}0},(21)$

where ${\mathbf{U}}_0$, $\mathbf{\Lambda }$ and ${\mathbf{M}}_2$ are the matrices specified in Supplementary Equations S8, S7, S11, respectively.

Note, the right-hand side of Eq. 21 defines a $2\pi$ -periodic ($4\pi$ -periodic) function for real $k_1$ when $n_2$ is even (odd).

If the gyricity is zero and the load acts in the horizontal (vertical) direction, the solution in Eq. 21 describes a vector function whose first component has even (odd) real and imaginary parts as functions of $k_1$, whereas the second component has odd (even) real and imaginary parts. When gyricity is non-zero, these components have neither even nor odd real and imaginary parts. Such properties can be observed in Figure 2, where we report the horizontal and vertical components of the Fourier transform of the steady-state solution ${\mathit{U}}_0^{\text{F}}$, when ${\text{Ω}}^{\text{*}}=0$ (parts (A) and (B)) and ${\text{Ω}}^{\text{*}}=1$ (parts (C) and (D)) for a load acting in the horizontal direction. By further inspection of the analytical solution in Eq. 21, we pose the attention on the numerator in $h_j$ ($j=\mathrm{1,2}$), belonging to ${\mathbf{U}}_0$ and ${\mathbf{M}}_2$ (see Supplementary Equations S9, S11), where the presence of gyricity induces a competition between terms and the amplitude of the components depends on the sign of the wave number. This feature of the solution in Eq. 21 for ${\text{Ω}}^{\text{*}}\ne 0$ is responsible for the symmetry breaking in the considered problem (see also (Nieves et al., 2020)).

FIGURE 2

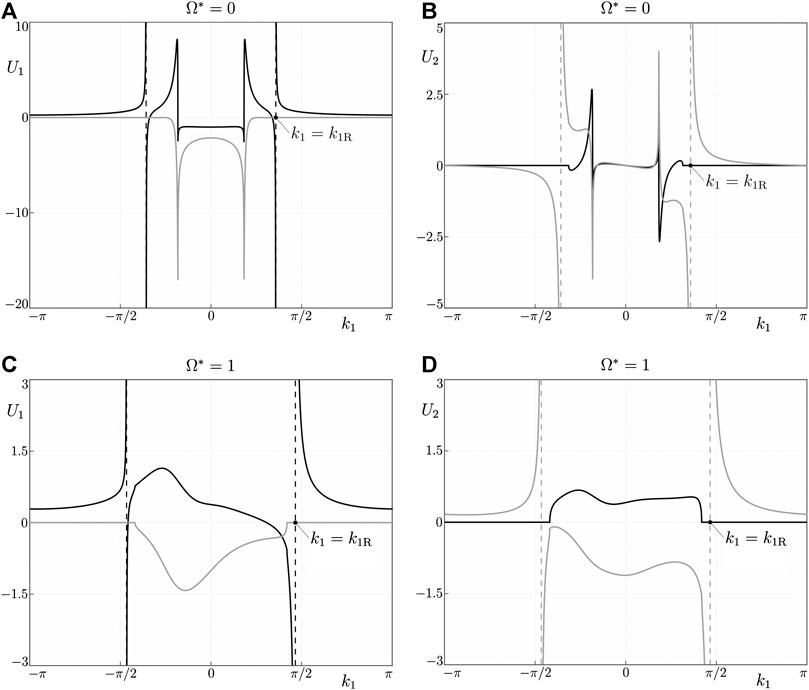
FIGURE 2. Plots of the discrete Fourier transform of the steady-state solution in Eq. 21, for $n_2=0$. Parts A,C(B,D) show the first (second) component of ${\mathit{U}}_0^{\text{F}}$ for ${\text{Ω}}^{\text{*}}=0$ and ${\text{Ω}}^{\text{*}}=1$, respectively. The real parts of the components are represented by black curves, whereas the imaginary parts are indicated by gray curves. The vertical dashed lines represent the wave numbers $\pm k_{1\text{R}}$ for which these components are singular, having simple poles. The computations are performed for ${\omega }_0=0.8$ and $\mathit{P}={\left(\mathrm{1,0}\right)}^{\text{T}}$.

2.5 The Displacements in the Forced Lattice and Associated Wave Phenomena

The displacements in the lattice can be found from inverting the discrete Fourier transform, taking into account the periodicity properties of Eq. 21. Then, the displacements of the nodes in the lattice are given by

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)=\text{Re}\left({\mathcal{U}}^{\left(n_1,n_2\right)}{e}^{\text{i}{\omega }_{0}t}\right),(22)$

where

${\mathcal{U}}^{\left(n_1,n_2\right)}=\{\begin{array}{cc}\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{\mathbf{U}}_{n_2}^{\text{F}}{e}^{-\text{i}{k}_1(n_1+n_2/2)}\text{d}{k}_1},& \text{if }{n}_2\text{is}\text{even},\\ \frac{1}{4\pi }{\displaystyle {\int }_{-2\pi }^{2\pi }{\mathbf{U}}_{n_2}^{\text{F}}{e}^{-\text{i}{k}_1(n_1+n_2/2)}\text{d}{k}_1},& \text{if}{n}_2\text{is}\text{odd}.\end{array}(23)$

Here, we note that ${\mathcal{U}}^{\left(n_1,n_2\right)}={\text{lim}}_{t\to +\infty }{\mathbf{U}}^{\left(p,n_2\right)}\left(t\right)$, where $p=2n_1$ and the complex time-dependent amplitude ${\mathbf{U}}^{\left(p,n_2\right)}\left(t\right)$ were introduced in Section 2.2.

2.5.1 The Rayleigh Waves

Rayleigh waves carry some of the energy produced by the point load in both directions along the boundary. The lack of symmetry in the integral kernel of Eq. 23 with respect to the zero wave number results in a disparity between amplitudes of waves outgoing from the source to the left and to the right of the load.

The Rayleigh waves are defined by the degenerate values of the wave number of ${\mathbf{M}}_2$ for a given frequency ${\omega }_0$, and these singular points are represented by the simple poles of Eq. 21. One can check that there exist no other singular points of this function for ${\omega }_0\ne {\text{Ω}}^{\text{*}}$ (the special case ${\omega }_0={\text{Ω}}^{\text{*}}$ will be discussed later). On the dispersion diagram, these simple poles correspond to the intersections of the line $\omega ={\omega }_0$ with the curve $\omega ={\omega }_{\text{R}}$, where ${\omega }_{\text{R}}$ is given by

${\omega }_{\text{R}}=\sqrt{3{\sin }^2\left(\frac{k_1}{2}\right)+\frac{{\left({\text{Ω}}^{\text{*}}\right)}^2}{2}-\sqrt{{\left[3{\sin }^2\left(\frac{k_1}{2}\right)+\frac{{\left({\text{Ω}}^{\text{*}}\right)}^2}{2}\right]}^2-6{\sin }^4\left(\frac{k_1}{2}\right)}},(24)$

and represents the dispersion curve of the system associated with Rayleigh waves.¹ The dispersion curve is plotted in Figure 3.

FIGURE 3

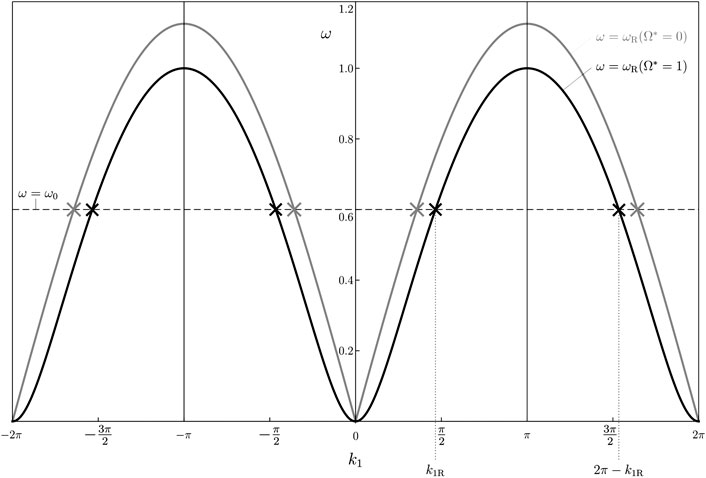
FIGURE 3. Dispersion diagram for $k_1\in [-2\pi ,2\pi ]$, relevant for Eq. 23 when $n_2$ is odd. The black (gray) curve indicates the function ${\omega }_{\text{R}}$ for ${\text{Ω}}^{\text{*}}=1$ (${\text{Ω}}^{\text{*}}=0$). The line $\omega ={\omega }_0$ is shown for ${\omega }_0=0.6$. The intersections of this line with the curve of ${\omega }_{\text{R}}$ for ${\text{Ω}}^{\text{*}}=1$ (${\text{Ω}}^{\text{*}}=0$) are represented by black (gray) crosses. The interval $[-\pi ,\pi ]$ is instead relevant for Eq. 23 when $n_2$ is even. Wave numbers $k_1=k_{1\text{R}}$ and $2\pi -k_{1\text{R}}$, defining singular points of Eq. 21, are also shown.

In Figure 3 we limit our attention to the intervals of periodicity for Eq. 21 mentioned in Section 2.4. Since ${\omega }_0-\text{i}0$ is present in Eq. 21, as discussed in Section 2.3, the degenerate wave numbers of Eq. 21 are perturbed and are slightly shifted from the real $k_1$ -axis in the complex plane. The causality principle enables the new locations of these points to be determined using information concerning the group velocity $v_g=\text{d}{\omega }_{\text{R}}/\text{d}{k}_1$ (see also (Slepyan, 2002)). In particular, if at the previously mentioned intersection points $v_g>0$ ($v_g<0$) the frequency ${\omega }_0$ and the corresponding wave number $k_1$ define waves propagating to the right (left) of the load. Additionally, when the frequency is ${\omega }_0-\text{i}0$, the associated degenerate value of Eq. 21 is located at $k_1-\text{i}0$ ($k_1+\text{i}0$). Consequently, the dispersion diagram in Figure 3 predicts that the degenerate values required later for the computation of outgoing waves from the source are at $k_1=\pm k_{1\text{R}}\mp \text{i}0$ and $k_1=\pm \left(2\pi -k_{1\text{R}}\right)\pm \text{i}0$.

Using the above information, we can calculate the form of the Rayleigh waves produced by the point load by determining the simple poles of Eq. 23 and employing the residue theorem to compute Eq. 23 at a point located far from the application point of the oscillatory force. With this approach, it is possible to show that for $n_2=0$

${\mathbf{u}}^{\left(n_1,0\right)}\left(t\right)\sim \text{Im}\left({\mathcal{A}}_{+}^{\left(0\right)}\left(k_{1\text{R}}\right)e^{\text{i}\left({\omega }_{0}t-k_{1\text{R}}{n}_1\right)}\right)\text{for}{n}_1\to \infty ,(25)$

where the term on the right-hand side is the Rayleigh wave produced to the right of the point load. On the other hand, we have

${\mathbf{u}}^{\left(n_1,0\right)}\left(t\right)\sim \text{Im}\left({\mathcal{A}}_{-}^{\left(0\right)}\left(-k_{1\text{R}}\right)e^{\text{i}\left({\omega }_{0}t+k_{1\text{R}}{n}_1+\pi \right)}\right)\text{for}{n}_1\to -\infty ,(26)$

where the right-hand side defines the Rayleigh wave traveling away from the load to the left. Here,

${\mathcal{A}}_{\pm }^{\left(n_2\right)}\left(k_1^{\text{*}}\right)=\left(\begin{array}{c}{\mathcal{A}}_1^{\left(n_2,\pm \right)}\left(k_1^{\text{*}}\right)\\ {\mathcal{A}}_2^{\left(n_2,\pm \right)}\left(k_1^{\text{*}}\right)\end{array}\right)=\underset{k_1\to k_1^{\text{*}}\mp \text{i}0}{\text{lim}}\left(k_1-k_1^{\text{*}}\pm \text{i}0\right){\mathbf{U}}_{n_2}^{\text{F}},(27)$

$={\underset{k_1\to k_1^{\text{*}}\mp \text{i}0}{\text{lim}}\left(k_1-k_1^{\text{*}}\pm \text{i}0\right){\mathbf{U}}_0{\mathbf{\Lambda }}^{n_2}{\left[{\mathbf{M}}_2\right]}^{-1}\mathbf{P}|}_{{\omega }_0={\omega }_0-\text{i}0}.(28)$

It can be verified that when ${\text{Ω}}^{\text{*}}\ne 0$

$\left|{\mathcal{A}}_1^{\left(n_2,\pm \right)}\left(k_1^{\text{*}}\right)\right|\ne \left|{\mathcal{A}}_1^{\left(n_2,\pm \right)}\left(-k_1^{\text{*}}\right)\right|\text{and}\left|{\mathcal{A}}_2^{\left(n_2,\pm \right)}\left(k_1^{\text{*}}\right)\right|\ne \left|{\mathcal{A}}_2^{\left(n_2,\pm \right)}\left(-k_1^{\text{*}}\right)\right|.(29)$

Hence, the resulting dynamic response at the boundary of the semi-infinite gyro-elastic lattice to the far left and right of the point load is different. Moreover, these outwardly-propagating boundary waves cause the nodes to follow elliptical trajectories, as shown by the eigenmode analysis developed by Nieves et al. (2020).

2.5.2 Bulk Wave Radiation

Waves are also radiated along the rows of the lattice in the bulk. As $n_2\to \infty$, the amplitudes of such waves decrease. These waves are again attributed to the singular points of Eq. 21 associated with $k_1=\pm k_{1\text{R}}\mp \text{i}0,\pm \left(2\pi -k_{1\text{R}}\right)\pm \text{i}0$, which also define Rayleigh waves along the boundary. The form of the waves depends on the row of the lattice considered and it is obtained following the same procedure outlined in Section 2.5.1.

For $n_2>0$ with $n_2$ even, the displacements to the far right of the lattice behave as

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)\sim \text{Im}\left({\mathcal{A}}_{+}^{\left(n_2\right)}\left(k_{1\text{R}}\right)e^{\text{i}\left[{\omega }_{0}t-k_{1\text{R}}(n_1+n_2/2)\right]}\right)\text{for}{n}_1\to \infty ,(30)$

where the term on the right-hand side describes a wave traveling along the row defined by $n_2>0$ to the right. On the other hand, we have

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)\sim \text{Im}\left({\mathcal{A}}_{-}^{\left(n_2\right)}\left(-k_{1\text{R}}\right)e^{\text{i}\left[{\omega }_{0}t+k_{1\text{R}}(n_1+n_2/2)+\pi \right]}\right)\text{ for}{n}_1\to -\infty ,(31)$

where the term on the right-hand side represents a wave propagating to the left along the row $n_2>0$. We note that for the wave numbers $k_1=\pm k_{1\text{R}},\pm \left(2\pi -k_{1\text{R}}\right)$ and the frequency ${\omega }_0-\text{i}0$, the functions ${\text{Λ}}_j$, $j=\mathrm{1,2}$, are complex with modulus less than unity. Hence, the matrix ${\mathbf{\Lambda }}^{n_2}$ in Eq. 21 ensures that these waves have a decreasing amplitude for increasing $n_2$.

For rows in the lattice defined by odd $n_2$, we recall that Eq. 21 is a $4\pi$ -periodic function in $k_1$. Hence, the inversion formula for the discrete Fourier transform is as presented in the second equation in Eq. 23. In this case, a slightly modified procedure is required to compute the waves radiated in the bulk, taking into account the singular points of the function Eq. 21 on the interval $\left[-2\pi ,2\pi \right]$. For odd $n_2$, the displacements for $n_1\to \infty$ are

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)\sim \frac{1}{2}\text{Im}\left(\left[{\mathcal{A}}_{+}^{\left(n_2\right)}\left(k_{1\text{R}}\right)-{\mathcal{A}}_{+}^{\left(n_2\right)}\left(k_{1\text{R}}-2\pi \right)\right]e^{\text{i}\left[{\omega }_{0}t-k_{1\text{R}}(n_1+n_2/2)\right]}\right),(32)$

whereas for $n_1\to -\infty$ we have

${\mathbf{u}}^{\left(n_1,n_2\right)}\left(t\right)\sim \frac{1}{2}\text{Im}\left(\left[{\mathcal{A}}_{-}^{\left(n_2\right)}\left(-k_{1\text{R}}\right)-{\mathcal{A}}_{-}^{\left(n_2\right)}\left(2\pi -k_{1\text{R}}\right)\right]e^{\text{i}\left[{\omega }_{0}t+k_{1\text{R}}(n_1+n_2/2)+\pi \right]}\right).(33)$

We point out that the amplitudes of the waves along the odd rows of the lattice, specified in Eqs. 32,33, take into account the contributions from the wave numbers $k_1=\pm \left(2\pi -k_{1\text{R}}\right)$ (see Figure 3).

There also exist preferential directions for energy radiation in the bulk. When the gyricity is zero, along these specific lines in the lattice, the nodal displacements decay slowly as $O\left(n_2^{-1/3}\right)$ for $n_2\to \infty$, as shown by Slepyan (2010). These directions can be identified by determining when ${\text{Λ}}_j$, involved in Eq. 21, is complex with $\left|{\text{Λ}}_j\right|=1,$$j=\mathrm{1,2}$, for the frequency equal to ${\omega }_0$. As discussed by Slepyan (2010), this effect is purely attributed to the lattice’s micro-structure and is not found in the analogous continuous model. When the gyricity ${\text{Ω}}^{\text{*}}\ne 0$ is introduced, preferential directions for wave propagation can remain and increasing the gyricity causes the associated displacement amplitudes to decrease.

2.5.3 Resonant Modes

Next, we discuss the resonant case when the steady-state solution to the considered problem does not exist. We show this by investigating the derived solution in Eq. 21 along the boundary, where $n_2=0$.

When $k_1\to 0$, for either horizontal or vertical loading at the lattice boundary, the solution in Eq. 21 is bounded for ${\omega }_0\ne {\text{Ω}}^{\text{*}}$ and admits the following asymptotic representation:

${\mathbf{U}}_0^{\text{F}}=\frac{{\mathbf{C}}_0}{\sqrt{D\left({\text{Ω}}^{\text{*}},{\omega }_0\right)}}+O\left(k_1\right),k_1\to 0,(34)$

where

$D\left({\text{Ω}}^{\text{*}},{\omega }_0\right)=-6{\omega }_0^2+3\sqrt{{\omega }_0^2\left(3{\left({\text{Ω}}^{\text{*}}\right)}^2+{\omega }_0^2\right)}(35)$

and ${\mathbf{C}}_0$ denotes a constant vector with non-zero entries depending on the gyricity ${\text{Ω}}^{\text{*}}$, the frequency ${\omega }_0$ and the load amplitude $\mathbf{P}$. Clearly, $D\left({\text{Ω}}^{\text{*}},{\omega }_0\right)=0$ when ${\omega }_0={\text{Ω}}^{\text{*}}$. In this degenerate case, the asymptote near $k_1\to 0$ takes the form

${\mathbf{U}}_0^{\text{F}}=\frac{1}{\sqrt{3}}\frac{{\mathbf{S}}_0}{\sqrt{k_1-\text{i}0}\sqrt{k_1+\text{i}0}}+O\left(1\right),k_1\to 0,(36)$

that indicates the appearance of other singular points near $k_1=0$ in the solution in Eq. 21. In the above, if the load is horizontal (vertical) the vector ${\mathbf{S}}_0={\left(-\text{i},-1\right)}^{\text{T}}$ (${\mathbf{S}}_0={\left(1,-\text{i}\right)}^{\text{T}}$).

We note that the singular points in this asymptote approach each other as the Laplace transform parameter $s\to +0$, with their limiting location being the real axis at $k_1=0$. An illustration showing the typical behavior of the first component of Eq. 21 in this case is given in Figure 4A. There, the kernel has a simple pole for positive wave numbers but not for negative wave numbers, which implies that the structure does not support Rayleigh waves propagating to the left of the load on the boundary. The second component of Eq. 21 possesses the same singular features. Further to Eq. 36, in this situation ${\mathbf{U}}_0^{\text{F}}$ can be written in the form:

${\mathbf{U}}_0^{\text{F}}=\frac{1}{\sqrt{3}}\frac{{\mathbf{S}}_0}{\sqrt{k_1-\text{i}0}\sqrt{k_1+\text{i}0}}+{\mathbf{W}}_0^{\text{F}}+{\mathbf{B}}_0^{\text{F}},(37)$

where ${\mathbf{W}}_0^{\text{F}}$ represents the term that is singular at $k_1=k_{1\text{R}}-\text{i}0$ of Eq. 21 and ${\mathbf{B}}_0^{\text{F}}$ is a bounded function for $k_1\in \left[-\pi ,\pi \right]$. Upon applying the inverse of the discrete Fourier transform, while the last two terms in the right-hand side of Eq. 37 give bounded contributions to the displacement, the first term leads to a function that is singular for $x_1=n_1+n_2/2=0$ and $s\to +0$. Hence, the displacement at the location of the load is unbounded for $t\to +\infty$.

FIGURE 4

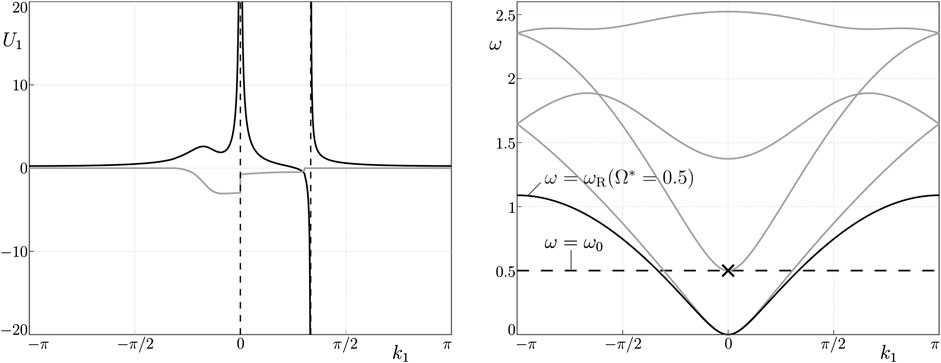
FIGURE 4. (A) The first component of the steady-state solution for the case of horizontal forcing on the boundary, with unit amplitude, when ${\omega }_0={\text{Ω}}^{\text{*}}$. The black (gray) curve represents the real (imaginary) part of this component. (B) The dispersion diagram for ${\omega }_0={\text{Ω}}^{\text{*}}$. The dispersion curve for Rayleigh waves is represented by the black curve, based on Eq. 24. The horizontal black dashed line represents ${\omega }_0=0.5$, which intersects the gray curves corresponding to $\left|{\text{Λ}}_j\right|=1$ ($j=\mathrm{1,2}$). The point $\left(k_1,{\omega }_0\right)=\left(0,{\text{Ω}}^{\text{*}}\right)$, indicated by the cross, corresponds to a resonance mode of the system. The computations in (A) and (B) have been performed for ${\text{Ω}}^{\text{*}}=0.5$.

The asymptotic representation in Eq. 36 is also in agreement with the dispersion diagram for ${\omega }_0={\text{Ω}}^{\text{*}}$, shown in Figure 4B. The associated horizontal line on this diagram intersects the curves along which $\left|{\text{Λ}}_j\right|=1$ ($j=\mathrm{1,2}$), represented by gray lines. These additional curves are useful in characterizing the main contribution of the integral contained in Eq. 23 in describing the lattice far-field and are connected with the appearance of waveforms and preferential directions in the bulk lattice (see also Slepyan (2010)). At $k_1=0$ on the dispersion diagram, the group velocity at the associated intersection point is zero (see Figure 4B, where at the point $\left(k_1,{\omega }_0\right)=\left(0,{\text{Ω}}^{\text{*}}\right)$ the group velocity is zero). Physically, such a point represents a resonance mode of the considered system, as discussed in (Slepyan, 2002, Section 3.3.5). The energy associated with this mode is unable to leave the location where the force is applied. Thus, the energy density at this location becomes unbounded as $t\to +\infty$. In other words, in the case ${\omega }_0={\text{Ω}}^{\text{*}}$ the steady-state solution does not exist.

2.6 Determination of Energy Flow in the Steady-State Regime

In this section, we analyze the energy carried by the Rayleigh waves and by the waves radiated into the bulk of the gyroscopic lattice by calculating the energy flow through the boundary of a sufficiently large region of the medium, as shown in Figure 5. The considered region is the rectangle S enclosed by the half-plane boundary and by the segments $\partial S_i$ ($i=1,\dots ,4$), indicated in Figure 5.

FIGURE 5

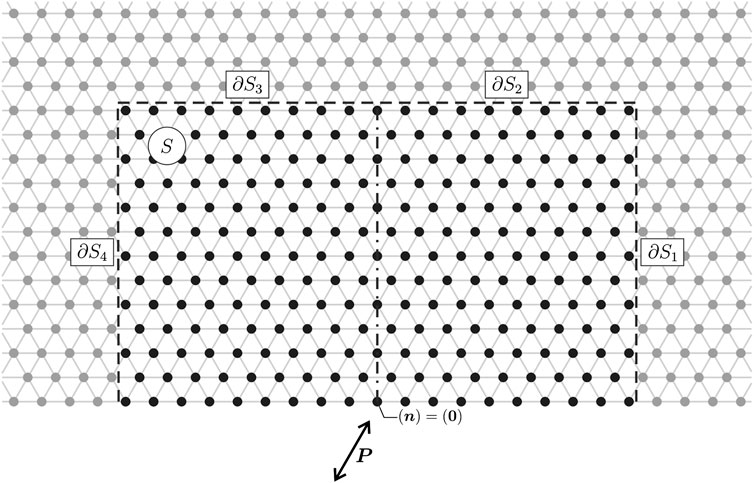
FIGURE 5. Region S of the gyroscopic lattice, delimited by the half-plane boundary and the segments $\partial S_i$ ($i=1,\dots ,4$), through which the energy flow is calculated.

In the steady-state regime, the rate at which energy is introduced into the system through the action of an oscillating point load applied at the node $\left(n_1,n_2\right)=\left(\mathrm{0,0}\right)$, having the vector amplitude $\mathbf{P}$ and frequency ${\omega }_0$, can be computed using the formula:

$W^{\text{in}}=\frac{1}{2}{\omega }_0\text{Im}\left(\mathbf{P}\cdot \overline{{\mathcal{U}}^{\left(\mathrm{0,0}\right)}}\right),(38)$

where the overline denotes the complex conjugate and ${\mathcal{U}}^{\left(n_1,n_2\right)}$ is defined in Eq. 23. The rate at which energy flows through each segment $\partial S_i$ is given by the classical formula introduced by Brillouin (see Chapter V in Brillouin (1953)):

$W_i^{\text{out}}=-\frac{1}{2}{\omega }_0\text{Im}\left({\displaystyle \sum _{{\mathit{n}}_j\in D_i}{\mathbf{F}}^{\left({\mathbf{n}}_j\right)}\cdot \overline{{\mathcal{U}}^{\left({\mathbf{n}}_j\right)}}}\right),(39)$

for $1\le i\le 4$. In Eq. 39, ${\mathbf{F}}^{\left({\mathbf{n}}_j\right)}$ represents the elastic force supplied by the nodes outside the considered region and connected to the node indicated by ${\mathbf{n}}_j$, positioned in the immediate proximity of $\partial S_i$, within S. The set of the nodes with multi-indices ${\mathbf{n}}_j$ located in the vicinity of $\partial S_i$, inside S, is denoted by $D_i$. For the conservation of energy law, the following equality is satisfied:

$W^{\text{in}}={\displaystyle \sum _{i=1}^4{W}_i^{\text{out}}}.(40)$

In Section 3, the above formulae for the energy flow will be used to show quantitatively that the presence of gyroscopic spinners breaks the symmetry of energy propagation with respect to a vertical line passing through the application point of the load.

2.7 Finite Element Model

The results of the analytical formulation illustrated in the previous sections will be verified with a finite element model built in the commercial software Comsol Multiphysics (version 5.4).

The numerical model consists of massless truss elements and point masses inserted at the lattice’s nodes. The effect of gyricity is simulated by imposing at each node a force that is proportional to the velocity, as in the first term on the right-hand side of the governing Eq. 2. Here the computational domain is finite, while the analytical treatment developed above is for a semi-infinite medium. In particular, the lattice has dimensions $100\times 46\sqrt{3}$. Adaptive Absorbing Layers (AAL) are introduced close to the top and vertical boundaries, in order to prevent waves from being reflected at these boundaries. AAL are created by assigning to the links located inside those regions a complex elastic modulus. A point load is applied to the middle point of the bottom boundary of the domain. The numerical simulations are performed in the time-harmonic regime.

3 Results

3.1 The Displacement Field in the Semi-Infinite Gyro-Elastic Lattice Loaded on the Boundary

In this section, we show the response of the semi-infinite lattice with embedded gyroscopic spinners to a point force applied on the boundary. In particular, we investigate how the gyricity affects the behavior of Rayleigh waves traveling along the boundary and of the waves propagating into the bulk of the medium.

Figure 6 shows the total displacement amplitude calculated at each node of the discrete system, produced by an oscillating force applied on the boundary. The results are based on the solution in Eq. 22, derived in Section 2. The force has unit amplitude and frequency ${\omega }_0=0.6$, and it acts in the horizontal (vertical) direction in parts (A) and (C) (parts (B) and (D)).

FIGURE 6

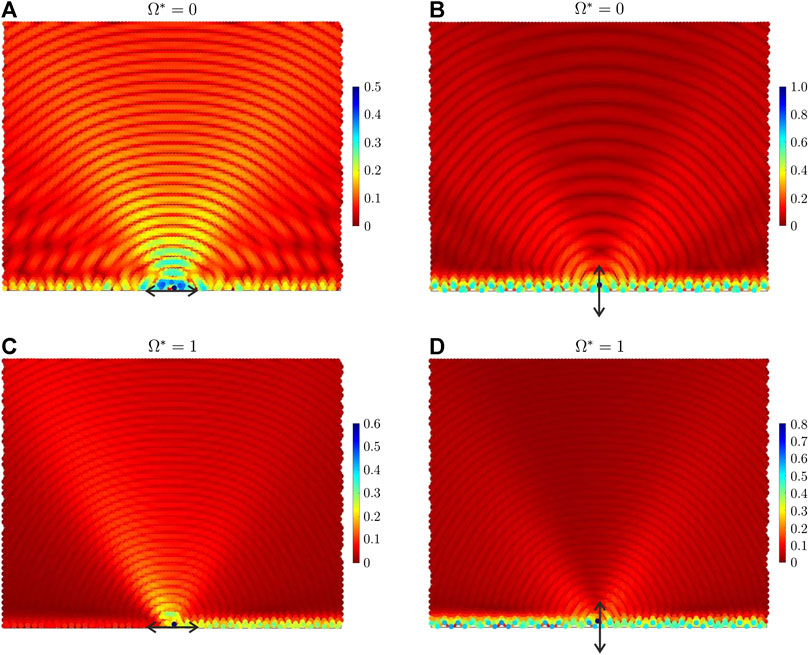
FIGURE 6. Total displacement amplitude field in the elastic lattice, obtained from the analytical formulation developed in Section 2, due to a (A,C) horizontal and (B,D) vertical point force applied on the boundary. In each figure, the force is represented by an arrow. The effective gyricity is (A,B)${\text{Ω}}^{\text{*}}=0$ and (C,D)${\text{Ω}}^{\text{*}}=1$.

In parts (A) and (B) of Figure 6 the effective gyricity is set equal to zero. It is apparent that when ${\text{Ω}}^{\text{*}}=0$ the response of the system is symmetric with respect to the point of application of the force. This in agreement with the classical theory on Rayleigh wave propagation in elastic lattices without gyroscopic effects. We also observe that in the vicinity of the load there exist evanescent modes, which induce localized deformations in the neighboring links. In the bulk there are preferential directions along which waves are radiated from the source, as described in Section 2.5.2. The region between these rays show outwardly propagating oscillations that decay like $O\left(n_2^{-1/2}\right)$. Comparing parts (A) and (B), we note that in (B) there exist waves with larger amplitudes. Moreover, by looking at the wavelengths, we observe that the bulk waves generated by a horizontal force are of the shear type, while the vertical force induces bulk waves of the pressure type, as expected.

Figures 6C,D illustrate the total displacement amplitude field produced by a horizontal and vertical force, respectively, when the effective gyricity is ${\text{Ω}}^{\text{*}}=1$. As in Figures 6A,B, the force has unit amplitude and frequency ${\omega }_0=0.6$. The main difference between Figures 6A–D is that when the effective gyricity is non-zero the response of the system ceases to be symmetric with respect to the vertical line passing through the point of application of the force. In part (C) we note that the amplitude of Rayleigh waves propagating to the right of the force is much larger compared to that of the surface waves traveling to the left. In addition, the force appears to activate waves in its vicinity having significant amplitude and propagating at 120° to the positive horizontal axis. On the other hand, the displacement field produced by a vertical force (see part (D)) shows that the symmetry is still broken, but the amplitudes of the waves traveling to the right and to the left of the force along the boundary are now comparable.

We also point out that the non-symmetric displacement field in Figure 6 can be inverted by changing the sign of the effective gyricity ${\text{Ω}}^{\text{*}}$.

In Figure 7 we present the total displacement amplitude fields computed by using the finite element model developed in Comsol Multiphysics and described in Section 2.7. The values of the parameters are the same as those considered in Figure 6. Comparing Figures 6, 7, we observe that the numerical and analytical results show an excellent agreement. This confirms the validity and accuracy of the analytical treatment discussed in Section 2.

FIGURE 7

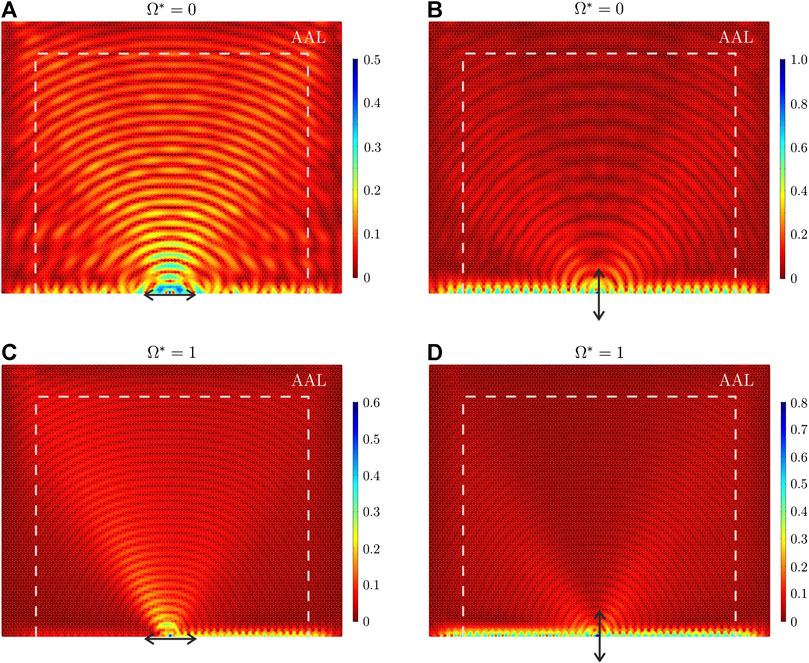
FIGURE 7. Same as in Figure 6, but obtained from numerical simulations performed in Comsol Multiphysics.

3.2 The Energy Flow

Here, we report the analytical results concerning the energy flow furnished by the external force, referred to as $W^{\text{in}}$, and the energy flow passing through each segment $\partial S_i$ in Figure 5, denoted as $W_i^{\text{out}}$ ($i=1,\dots ,4$). The formulae for $W^{\text{in}}$ and $W_i^{\text{out}}$ are given in Section 2.6.

As in Section 3.1, two different values of the effective gyricity are taken, namely ${\text{Ω}}^{\text{*}}=0$ and ${\text{Ω}}^{\text{*}}=1$. Moreover, two directions of the point load are considered, i.e. horizontal and vertical. The values of $W^{\text{in}}$ and $W_i^{\text{out}}$ for all the examined cases are summarized in Table 1.

TABLE 1

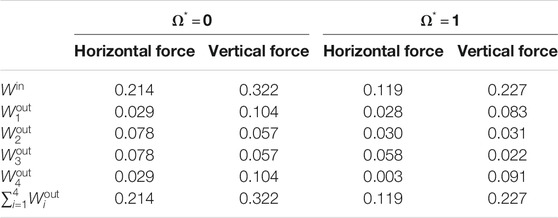
TABLE 1. Values of energy flows in the micro-structured lattice due to a horizontal or vertical force, when the effective gyricity is either ${\text{Ω}}^{\text{*}}=0$ or ${\text{Ω}}^{\text{*}}=1$.

By looking at Table 1, we notice that when the effective gyricity is zero $W_1^{\text{out}}+W_2^{\text{out}}=W_3^{\text{out}}+W_4^{\text{out}}$, implying that the response of the system is symmetric with respect to the application point of the force. The above equality ceases to hold when ${\text{Ω}}^{\text{*}}=1$. We also note that the energy partition between vertical and horizontal boundaries depends on the gyricity and on the direction of the force. Furthermore, for any of the four cases considered in Table 1, the energy balance is satisfied, since $W^{\text{in}}={{{\displaystyle \sum }}^{\text{}}}_{i=1}^4{W}_i^{\text{out}}$.

3.3 Parametric Analysis

In order to assess how the response of the micro-structured medium is affected by different physical quantities, we perform a parametric analysis where we vary the direction of the force, the radian frequency ${\omega }_0$ of the force and the effective gyricity ${\text{Ω}}^{\text{*}}$ of the spinners. The behavior of the medium is evaluated quantitatively by calculating the percentages of the energy flows $W_i^{\text{out}}$ passing through the boundaries $\partial S_i$ ($i=1,\dots ,4$) (see Figure 5) with respect to the energy input $W^{\text{in}}$ due to the external source.

In Figure 8 we show how the energy introduced into the system by the external oscillating force is divided into two parts, propagating in opposite directions relative to the position of the point force. In particular, the circles (squares) indicate the percentages of the energy flowing to the right (left) of the force with respect to the input energy flow. In Figure 8 it is assumed that the force acts in the horizontal direction. The five diagrams correspond to ${\text{Ω}}^{\text{*}}=\mathrm{0,0.25},0.5,0.75,1$; in each diagram, several values of the frequency ${\omega }_0$ of the point force are considered.

FIGURE 8

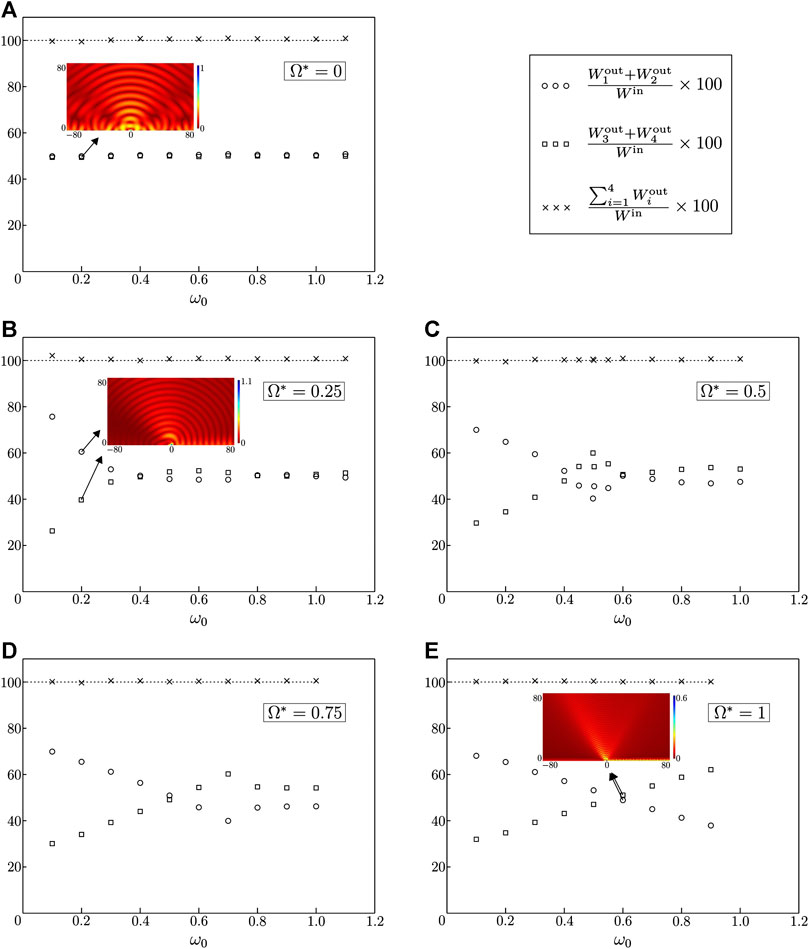
FIGURE 8. Percentages of energy flows propagating to the right ($W_1^{\text{out}}+W_2^{\text{out}}$) and to the left ($W_3^{\text{out}}+W_4^{\text{out}}$) of the point force with respect to the energy flow produced by the external load ($W^{\text{in}}$), calculated for several values of effective gyricity ${\text{Ω}}^{\text{*}}$ and frequency ${\omega }_0$. The results in this figure correspond to a point force acting in the horizontal direction. The insets illustrate the wave fields at specific frequencies ${\omega }_0$ and gyricities ${\text{Ω}}^{\text{*}}$.

In Figure 9 the values of the effective gyricity and of the frequency of the external source are identical to those considered in Figure 8, but the outcomes are obtained by applying a concentrated oscillating load acting in the vertical direction. In both Figures 8, 9, when ${\text{Ω}}^{\text{*}}=0$ the incoming energy is split into two equal contributions that propagate to the left and to the right of the force, both along the boundary and inside the bulk. Conversely, when ${\text{Ω}}^{\text{*}}\ne 0$ we observe a non-symmetrical distribution of energy in the system. We also notice that even when ${\text{Ω}}^{\text{*}}\ne 0$ the symmetry in the energy flow partition is retrieved for some specific values of the frequency, that change with the value of the effective gyricity. The crosses in both Figures 8, 9 represent the sums of the energy flow components traveling inside the system with respect to the input energy; it can be seen that, for every case considered, there is balance between input and output energy flows.

FIGURE 9

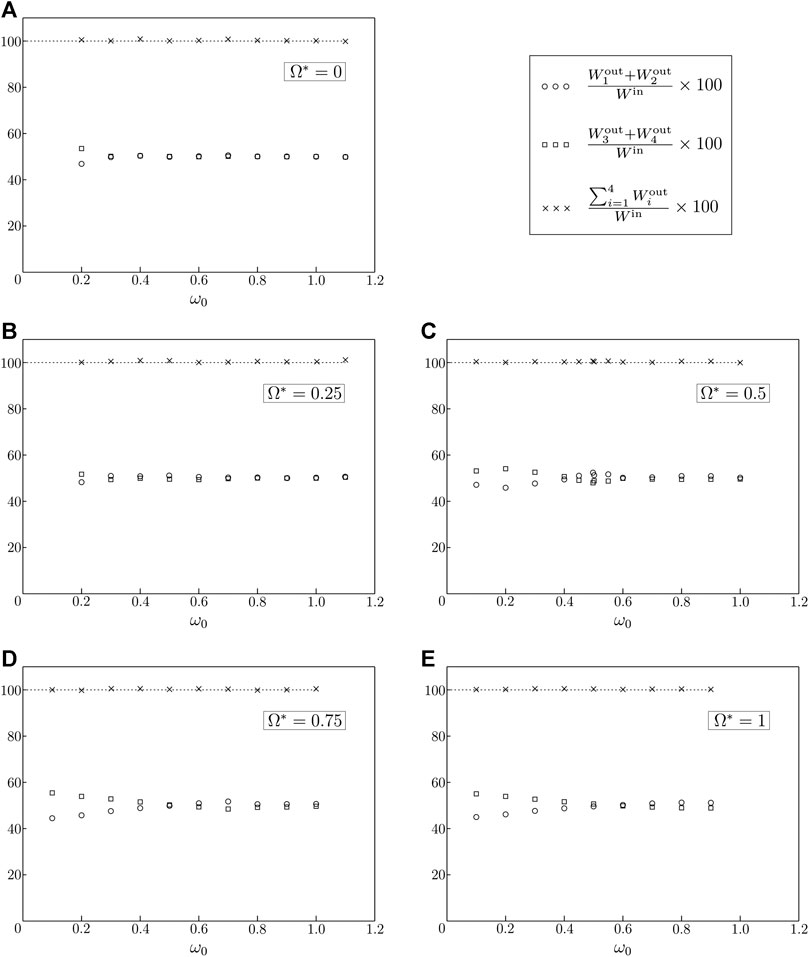
FIGURE 9. Same as in Figure 8, but for a vertically-acting point force.

The insets in Figure 8 present the color maps of the displacement fields, computed at given gyricities and frequencies of the external force. In part (A), where ${\text{Ω}}^{\text{*}}=0$, the wave pattern is clearly symmetric. When gyricity is introduced, as in part (B), the symmetry of the displacement field is broken, even if the frequency of the external force remains the same. In part (C), the wave pattern for a frequency near the intersection between the two sets of data is shown; in this case, the energy is split into two approximately equal parts traveling to the left and to the right of the load, but on each side the energy amounts propagating into the bulk and on the boundary are different. Here, it is apparent that the energy flowing into the bulk in the left-hand part of the lattice is approximately equal to the amount of energy carried in the right-hand part, where the energy is mainly concentrated on the boundary.

In Figures 10, 11 we focus the attention on Rayleigh waves, showing how the contributions of the energy flows corresponding to surface waves traveling to the right ($W_1^{\text{out}}$) and to the left ($W_4^{\text{out}}$) of the point load vary with the effective gyricity of the spinners and with the frequency of the external force. In Figure 10 (Figure 11) the force acts in the horizontal (vertical) direction. It is apparent that the direction of the force, the gyricity and the frequency all influence the response of the system and, in particular, the relative amount of total and surface energy propagating to the left and to the right of the applied force.

FIGURE 10

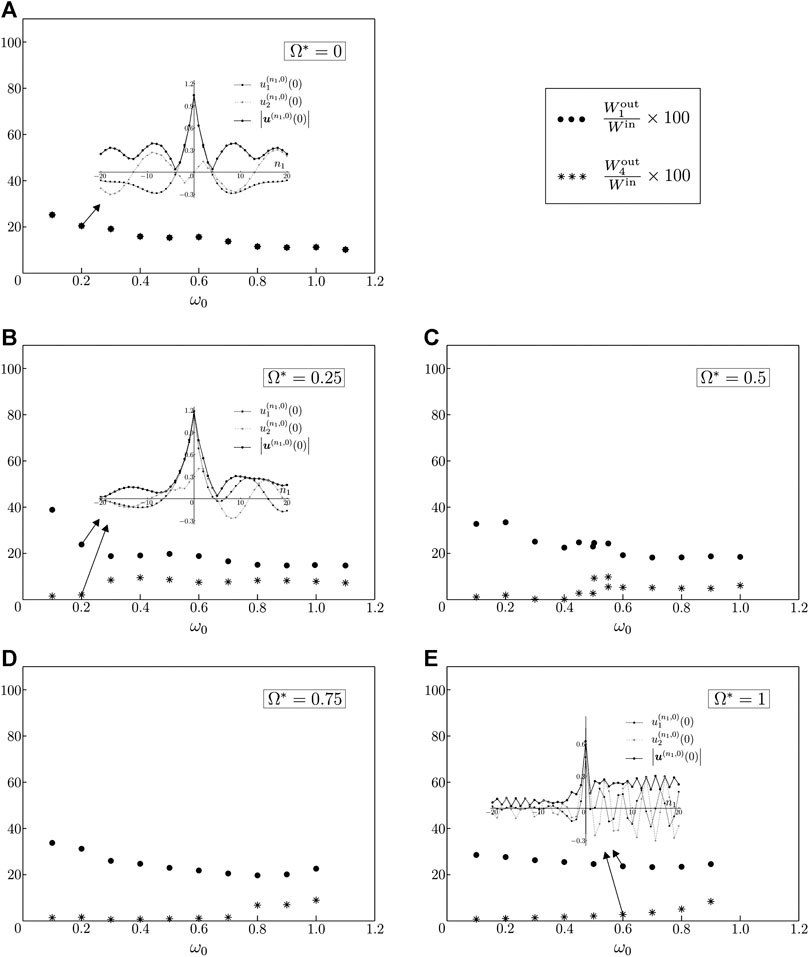
FIGURE 10. Energy flow percentages associated with Rayleigh waves traveling to the right and to the left of the point force, indicated by $W_1^{\text{out}}$ and $W_4^{\text{out}}$ respectively, for different values of effective gyricity and frequency of the external source. In these computations, the force acts in the horizontal direction. The insets show the displacements of the points on the lattice boundary, calculated at the frequencies indicated by the arrows.

FIGURE 11

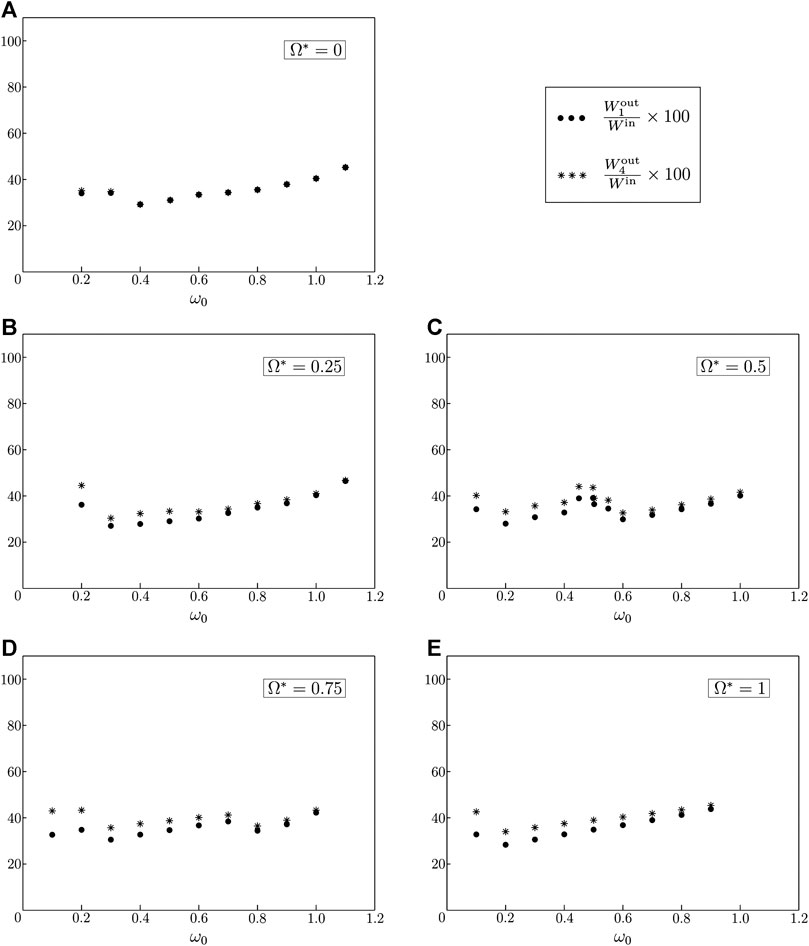
FIGURE 11. Same as in Figure 10, but for a vertically-acting point load.

The insets in Figure 10 illustrate, for different values of gyricity and frequency of the excitation, the amplitudes of the displacement components $u_1^{\left(n_1,0\right)}$ and $u_2^{\left(n_1,0\right)}$ of the lattice’s nodes at the boundary and the displacement magnitude $\left|{\mathbf{u}}^{\left(n_1,0\right)}\right|={\left[{\left(u_1^{\left(n_1,0\right)}\right)}^2+{\left(u_2^{\left(n_1,0\right)}\right)}^2\right]}^{1/2}$. The symmetry of the displacement field in the lattice without gyroscopic spinners, shown in Figure 10A, is broken when gyricity is incorporated into the system, as illustrated by the non-symmetric displacement profiles of Figures 10B,E.

Now, we consider a special case, where the surface waves propagating to the left of the point load exhibit a negligibly small amplitude. This can be obtained by taking the effective gyricity ${\text{Ω}}^{\text{*}}=0.5$, the frequency of the external force ${\omega }_0=0.35$ and applying a horizontally-acting force (see also Figures 8, 10). The displacement field for this choice of the parameters, presented in Figure 12, clearly shows that the energy coming from the external source propagates into the bulk and practically only to the right of the force along the boundary. A similar effect could also be achieved in the resonant case ${\omega }_0={\text{Ω}}^{\text{*}}$, but there the steady-state solution does not exist (see Section 2.5.3). The energy flow partition for the system in the neighborhood of ${\omega }_0={\text{Ω}}^{\text{*}}$ is investigated in Figure 8C, which shows that the energy flux distributions vary rapidly in the vicinity of ${\omega }_0={\text{Ω}}^{\text{*}}$.

FIGURE 12

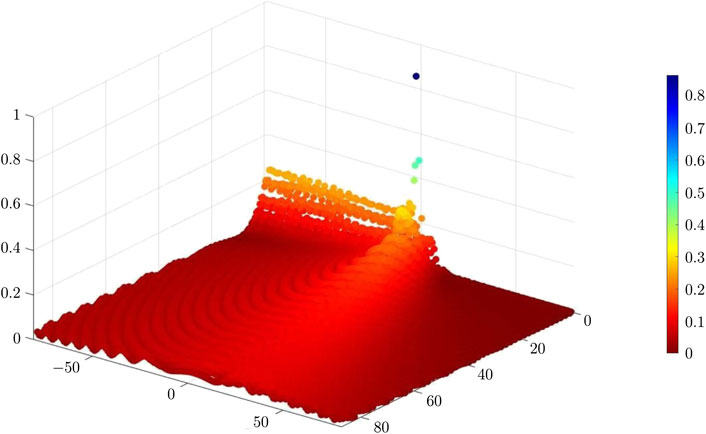
FIGURE 12. Displacement field of the lattice’s masses when ${\text{Ω}}^{\text{*}}=0.5$, ${\omega }_0=0.35$ and the point force acts in the horizontal direction.

Another interesting case is represented by the scenario where almost all the energy propagates along the boundary. This situation is shown in Figure 13, where ${\text{Ω}}^{\text{*}}=1$, ${\omega }_0=0.9$ and the point force acts in the vertical direction (see also Figures 9, 11). From the displacement field in this figure, it is apparent that most of the energy is localized at the boundary of the medium. Moreover, in this case the discrete system shows negligible preferential directionality (see also Figure 9E).

FIGURE 13

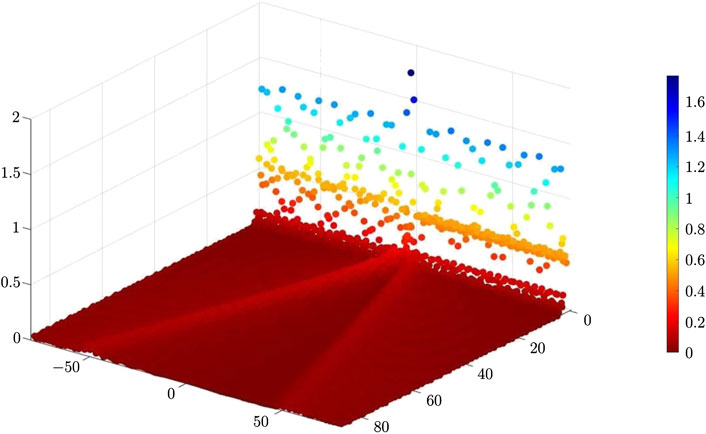
FIGURE 13. Displacement field of the lattice’s masses when ${\text{Ω}}^{\text{*}}=1$, ${\omega }_0=0.9$ and the point force acts in the vertical direction.

4 Discussion

The diagrams of the displacement amplitude fields in Figures 6, 7, as well as the values of the energy flows in Table 1, show that the gyricity is capable of breaking the symmetry in the energy propagation of both Rayleigh and bulk waves propagating from the external source. This is a consequence of the non-reciprocity of the gyro-elastic lattice.²

Examining the outcomes of the parametric analysis presented in Section 3.3, in particular Figures 8, 9, it is apparent that the distribution of energy in the system strongly depends on both the effective gyricity ${\text{Ω}}^{\text{*}}$ of the spinners and the radian frequency ${\omega }_0$ of the external oscillating force. Generally, at low frequencies it is easier to partition the energy flow into two significantly different contributions, propagating in opposite directions. Nonetheless, for any given value of the effective gyricity, it is possible to find one or more values of ${\omega }_0$ at which the energy is split into two equal parts. The lowest value of this frequency increases as the effective gyricity is increased. Comparing Figures 8, 9, we observe that the energy symmetry breaking is more evident when the force acts in the horizontal direction. Of course, for an inclined direction of the force, the response of the system can be determined from the principle of superposition by summing the effects due to the horizontally- and vertically-acting forces, since the considered problem is linear.

The investigation of the individual components of the energy flows associated with Rayleigh waves, presented in Figures 10, 11 for a horizontally- and vertically-acting point force respectively, reveals that the propagation of energy along the boundary of the medium is affected significantly by the direction of the force. In the case when ${\text{Ω}}^{\text{*}}=0$, the energy flow along the boundary is the same in both directions and it decreases (increases) as the frequency of the external source acting in the horizontal (vertical) direction is increased. On the other hand, when ${\text{Ω}}^{\text{*}}\ne 0$, the energy flowing to the right (left) is larger than in the opposite direction if the direction of the force is horizontal (vertical). Independently of the direction of the force, the difference between the energy flows in the two opposite directions generally decreases as the frequency is increased.

The parametric analysis discussed in Section 3.3 has been helpful in identifying special cases, where Rayleigh waves propagate only in one direction (see Figure 12) or where bulk waves have very small amplitudes compared with those of surface waves (see Figure 13).

The analytical formulation also made it possible to analyze resonant regimes where the steady-state solution cannot be reached (see Section 2.5.3).

The capability of the considered micro-structured system in creating preferential directionality in the propagation of waves can be exploited to design novel energy splitters, where the desired amount of energy propagating in a specific prescribed direction can be varied by changing the effective gyricity of the spinners. The tunability of the proposed model is an essential tool, that can be used in many practical applications where it is required to vary the output depending on the contingent needs. Important examples include electronic instruments converting mechanical energy into electric energy (and vice versa) and elastic filters that can be utilized both for protection and energy harvesting.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All the authors contributed to the discussion of the results and the revision of the manuscript. MN had a leading role in the analytical development of the problem, GC in the numerical computations, VP in the physical interpretation of the model and MB in the conceptualization of the work.

Funding

MN and MB gratefully acknowledge the financial support of the EU H2020 grant MSCA-IF-2016-747334-CAT-FFLAP. The program “Mobilità dei giovani ricercatori” financed by Regione Autonoma della Sardegna is also acknowledged (MB and VP).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.602960/full#supplementary-material.

Footnotes

¹The dispersion analysis for Rayleigh waves in a semi-infinite gyroscopic triangular lattice is discussed in detail by Nieves et al. (2020), where it is explicitly shown that the dispersion diagram remains symmetric.

²A formal proof of the non-reciprocity of the gyroscopic medium has been presented by Nieves et al. (2020).

References

Achenbach, J. D. (1973). “Wave propagation in elastic solids.” in North-holland series in applied mathematics and mechanics. Amsterdam, London: North-Holland Publishing Company, 16.

Google Scholar

Al Ba’ba’a, H., Yu, K., and Wang, Q. (2020). Elastically-supported lattices for tunable mechanical topological insulators. Extreme Mechanics Letters. 38, 100758. doi:10.1016/j.eml.2020.100758

CrossRef Full Text | Google Scholar

Antonakakis, T., Craster, R. V., Guenneau, S., and Skelton, E. A. (2014). An asymptotic theory for waves guided by diffraction gratings or along microstructured surfaces. Proc. Math. Phys. Eng. Sci. 470, 20130467. doi:10.1098/rspa.2013.0467

PubMed Abstract | CrossRef Full Text | Google Scholar

Armanini, C., Dal Corso, F., Misseroni, D., and Bigoni, D. (2017). From the elastica compass to the elastica catapult: an essay on the mechanics of soft robot arm. Proc. Math. Phys. Eng. Sci. 473, 20160870. doi:10.1098/rspa.2016.0870

PubMed Abstract | CrossRef Full Text | Google Scholar

Bacigalupo, A., De Bellis, M. L., and Gnecco, G. (2019). Complex frequency band structure of periodic thermo-diffusive materials by Floquet–Bloch theory. Acta Mech. 230, 3339–3363. doi:10.1007/s00707-019-02416-9

CrossRef Full Text | Google Scholar

Bi, L., Hu, J., Jiang, P., Kim, D. H., Dionne, G. F., Kimerling, L. C., et al. (2011). On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat. Photon. 5, 758–762. doi:10.1038/nphoton.2011.270

CrossRef Full Text | Google Scholar

Bordiga, G., Cabras, L., Piccolroaz, A., and Bigoni, D. (2018). Prestress tuning of negative refraction and wave channeling from flexural sources. Appl. Phys. Lett. 114. doi:10.1063/1.5084258

CrossRef Full Text | Google Scholar

Brillouin, L. (1953). Wave propagation in periodic structuresElectric filters and crystal lattices. Mineola, NY: Dover Publications, Inc.

Google Scholar

Brun, M., Jones, I. S., and Movchan, A. B. (2012). Vortex-type elastic structured media and dynamic shielding. Proc. Roy. Soc. Lond. 468, 3027–3046. doi:10.1098/rspa.2012.0165

CrossRef Full Text | Google Scholar

Carta, G., Jones, I. S., Movchan, N. V., Movchan, A. B., and Nieves, M. J. (2017). Deflecting elastic prism” and unidirectional localisation for waves in chiral elastic systems. Sci. Rep. 7, 26. doi:10.1038/s41598-017-00054-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Carta, G., Brun, M., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2014). Dispersion properties of vortex-type monatomic lattices. Int. J. Solid Struct. 51, 2213–2225. doi:10.1016/j.ijsolstr.2014.02.026

CrossRef Full Text | Google Scholar

Carta, G., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2020). Chiral flexural waves in structured plates: directional localisation and control. J. Mech. Phys. Solid. 137, 103866. doi:10.1016/j.jmps.2020.103866

CrossRef Full Text | Google Scholar

Carta, G., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2019). One-way interfacial waves in a flexural plate with chiral double resonators. Philosophical Transactions of the Royal Society A. 378, 20190350. doi:10.1098/rsta.2019.0350

CrossRef Full Text | Google Scholar

Carta, G., Nieves, M. J., Jones, I. S., Movchan, N. V., and Movchan, A. B. (2018). Elastic chiral waveguides with gyro-hinges. Q. J. Mech. Appl. Math. 71, 157–185. doi:10.1093/qjmam/hby001

CrossRef Full Text | Google Scholar

Colquitt, D. J., Craster, R. V., Antonakakis, T., and Guenneau, S. (2015). Rayleigh-Bloch waves along elastic diffraction gratings. Proc. Math. Phys. Eng. Sci. 471, 20140465. doi:10.1098/rspa.2014.0465

PubMed Abstract | CrossRef Full Text | Google Scholar

Filipov, E. T., Tachi, T., Paulino, G. H., and Weitz, D. A. (2015). Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl. Acad. Sci. U.S.A. 112, 12321–12326. doi:10.1073/pnas.1509465112

PubMed Abstract | CrossRef Full Text | Google Scholar

Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R., and Alù, A. (2014). Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science. 343, 516–519. doi:10.1126/science.1246957

PubMed Abstract | CrossRef Full Text | Google Scholar

Garau, M., Carta, G., Nieves, M. J., Jones, I. S., Movchan, N. V., and Movchan, A. B. (2018). Interfacial waveforms in chiral lattices with gyroscopic spinners. Proc. Roy. Soc. Lond. 474, 20180132. doi:10.1098/rspa.2018.0132

CrossRef Full Text | Google Scholar

Garau, M., Nieves, M. J., Carta, G., and Brun, M. (2019). Transient response of a gyro-elastic structured medium: unidirectional waveforms and cloaking. Int. J. Eng. Sci. 143, 115–141. doi:10.1016/j.ijengsci.2019.05.007

CrossRef Full Text | Google Scholar

Graff, K. F. (1975). Wave motion in elastic solids. Oxford, United Kingdom: Oxford University Press.

Google Scholar

Haslinger, S. G., Movchan, N. V., Movchan, A. B., Jones, I. S., and Craster, R. V. (2017). Controlling flexural waves in semi-infinite platonic crystals with resonator-type scatterers. Q. J. Mech. Appl. Math. 70, 216–247. doi:10.1093/qjmam/hbx005

CrossRef Full Text | Google Scholar

Lee, C. H., Li, G., Jin, G., Liu, Y., and Zhang, X. (2018). Topological dynamics of gyroscopic and Floquet lattices from Newton’s laws. Phys. Rev. B. 97, 085110. doi:10.1103/PhysRevB.97.085110

CrossRef Full Text | Google Scholar

Linton, C. M., and McIver, M. (2002). The existence of Rayleigh-Bloch surface waves. J. Fluid Mech. 470, 85–90. doi:10.1017/S0022112002002227

CrossRef Full Text | Google Scholar

Marder, M., and Gross, S. (1995). Origin of crack tip instabilities. J. Mech. Phys. Solid. 43, 1–48. doi:10.1016/0022-5096(94)00060-I

CrossRef Full Text | Google Scholar

Misseroni, D., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2016). Cymatics for the cloaking of flexural vibrations in a structured plate. Sci. Rep. 6, 23929. doi:10.1038/srep23929

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, N. P., Nash, L. M., and Irvine, W. T. M. (2018). Tunable band topology in gyroscopic lattices. Phys. Rev. B. 98, 174301. doi:10.1103/PhysRevB.98.174301

CrossRef Full Text | Google Scholar

Morvaridi, M., Carta, G., and Brun, M. (2018). Platonic crystal with low-frequency locally-resonant spiral structures: wave trapping, transmission amplification, shielding and edge waves. J. Mech. Phys. Solid. 121, 496–516. doi:10.1016/j.jmps.2018.08.017

CrossRef Full Text | Google Scholar

Nash, L. M., Kleckner, D., Read, A., Vitelli, V., Turner, A. M., and Irvine, W. T. (2015). Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. U.S.A. 112, 14495–14500. doi:10.1073/pnas.1507413112

PubMed Abstract | CrossRef Full Text | Google Scholar

Nieves, M. J., Carta, G., Jones, I. S., Movchan, N. V., and Movchan, A. B. (2018). Vibrations and elastic waves in chiral multi-structures. J. Mech. Phys. Solid. 121, 387–408. doi:10.1016/j.jmps.2018.07.020

CrossRef Full Text | Google Scholar

Nieves, M. J., Carta, G., Pagneux, V., and Brun, M. (2020). Rayleigh waves in micro-structured elastic systems: non-reciprocity and energy symmetry breaking. Int. J. Eng. Sci. 156, 103365. doi:10.1016/j.ijengsci.2020.103365

CrossRef Full Text | Google Scholar

Nieves, M. J., Movchan, A. B., Jones, I. S., and Mishuris, G. S. (2013). Propagation of Slepyan’s crack in a non-uniform elastic lattice. J. Mech. Phys. Solid. 61, 1464–1488. doi:10.1016/j.jmps.2012.12.006

CrossRef Full Text | Google Scholar

Piccolroaz, A., Gorbushin, N. A., Mishuris, G. S., and Nieves, M. J. (2020). Dynamic phenomena and crack propagation in dissimilar elastic lattices. Int. J. Eng. Sci. 149, 103208. doi:10.1016/j.ijengsci.2019.103208

CrossRef Full Text | Google Scholar

Porter, R., and Evans, D. V. (2005). Embedded Rayleigh-Bloch surface waves along periodic rectangular arrays. Wave Motion. 43, 29–50. doi:10.1016/j.wavemoti.2005.05.005

CrossRef Full Text | Google Scholar

Porter, R., and Evans, D. V. (1999). Rayleigh-Bloch surface waves along periodic gratings and their connection with trapped modes in waveguides. J. Fluid Mech. 386, 233–258. doi:10.1017/S0022112099004425

CrossRef Full Text | Google Scholar

Rayleigh, J. W. S. (1885). On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 17, 4–11. doi:10.1112/plms/s1-17.1.4

CrossRef Full Text | Google Scholar

Slepyan, L. I. (2002). Models and phenomena in fracture Mechanics. Berlin, Germany: Springer.

Google Scholar

Slepyan, L. I. (2010). Wave radiation in lattice fracture. Acoust Phys. 56, 962–971. doi:10.1134/S1063771010060217

CrossRef Full Text | Google Scholar

Sounas, D. L., Caloz, C., and Alù, A. (2013). Giant non-reciprocity at the subwavelength scale using angular momentum-biased metamaterials. Nat. Commun. 4, 2407. doi:10.1038/ncomms3407

PubMed Abstract | CrossRef Full Text | Google Scholar

Süsstrunk, R., and Huber, S. D. (2015). Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50. doi:10.1126/science.aab0239

PubMed Abstract | CrossRef Full Text | Google Scholar

Tallarico, D., Hannema, G., Miniaci, M., Bergamini, A., Zemp, A., and Van Damme, B. (2020). Superelement modelling of elastic metamaterials: complex dispersive properties of three-dimensional structured beams and plates. J. Sound Vib. 484, 115499. doi:10.1016/j.jsv.2020.115499

CrossRef Full Text | Google Scholar

Viktorov, I. A. (1967). Rayleigh and lamb waves. New York: Plenum Press.

CrossRef Full Text | Google Scholar

Wang, P., Lu, L., and Bertoldi, K. (2015). Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 115, 104302. doi:10.1098/rspa.2018.0132

PubMed Abstract | CrossRef Full Text | Google Scholar

Wenzel, M., Bursi, O. S., and Antoniadis, I. (2020). Optimal finite locally resonant metafoundations enhanced with nonlinear negative stiffness elements for seismic protection of large storage tanks. J. Sound Vib. 483, 115488. doi:10.1016/j.jsv.2020.115488

CrossRef Full Text | Google Scholar