An interpretable stacking ensemble model for high-entropy alloy mechanical property prediction

High-entropy alloys (HEAs) have attracted significant attention due to their excellent mechanical properties and broad application prospects. However, accurately predicting their mechanical behavior remains challenging because of the vast compositional design space and complex multi-element interactions. In this study, we propose a stacking learning-based machine learning framework to improve the accuracy and robustness of HEA mechanical property predictions. Key physicochemical features were extracted, and a hierarchical clustering model-driven hybrid feature selection strategy (HC-MDHFS) was employed to identify the most relevant descriptors. Three machine learning algorithms-Random Forest (RF), Extreme Gradient Boosting (XGBoost), and Gradient Boosting (Gradient Boosting)-were integrated into a multi-level stacking ensemble, with Support Vector Regression serving as the meta-learner. To improve model interpretability, the SHapley Additive Explanations (SHAP) method was applied to assess feature importance. The results demonstrate that the proposed stacking framework outperforms individual models in predicting yield strength and elongation, showing improved generalization ability and predictive accuracy.

1 Introduction

High-entropy alloys (HEAs), also referred to as multi-principal element alloys (MPEAs), were first introduced by Yeh et al. (2004) and Cantor et al. (2004). Initially, HEAs were defined as alloys comprising five or more principal elements, with atomic fractions between 5% and 35% (Yeh et al., 2004). This classification was based on the hypothesis that when multiple elements coexist in near-equiatomic proportions, the configurational entropy significantly increases, reducing the likelihood of intermetallic compound formation and promoting the stabilization of a single-phase solid solution. Over time, the definition of HEAs has expanded, and contemporary research generally considers any alloy composed of three or more principal elements in near-equiatomic ratios as a high-entropy alloy.

Benefiting from the combined effects of high-entropy, lattice distortion, sluggish diffusion, and the cocktail effect, HEAs have drawn increasing attention due to their unique physicochemical properties, which differ significantly from those of conventional alloys (Pickering and Jones, 2016). For instance, CrMnFeCoNi HEAs exhibit an excellent combination of strength and ductility at room temperature and maintain outstanding mechanical properties in low and ultra-low temperature environments (Liu et al., 2022). Similarly, refractory HEAs such as CrMoNbV demonstrate high yield strength and exceptional thermal softening resistance at elevated temperatures (1273 K), outperforming traditional Ni-based superalloys (Lee et al., 2021). These properties make HEAs highly suitable for demanding applications in aerospace, nu-clear energy, and extreme environmental conditions.

Another important aspect of HEAs is their remarkable stability, which can be attributed to the fact that in a certain macrostate, a sample can have many variants of states at the atomic level, without affecting the material’s external characteristics. This contributes to their exceptional stability, as described in previous studies on HEA mechanical properties (Maruschak and Maruschak, 2024).

Despite their promising mechanical characteristics, the vast compositional design space of HEAs and the complex nonlinear interactions between multiple elements pose significant challenges to their efficient design and optimization. Traditional experimental approaches are costly and time-intensive, limiting their ability to explore the full range of possible HEA compositions. Additionally, computational modeling methods, including Density Functional Theory (DFT) (Zhang et al., 2014), Ab Initio Molecular Dynamics (AIMD) (Gao and Alman, 2013), Molecular Dynamics (MD) (Wang Q. et al., 2024), and Finite Element Analysis (FEA), have been employed to predict HEA properties. While these techniques provide valuable theoretical insights, they are computationally expensive and often struggle to handle the high-dimensional compositional space characteristic of HEAs (Guo et al., 2023).

Machine learning (ML) has recently emerged as a powerful data-driven approach to overcoming these limitations. By leveraging large datasets of experimental and computational results, ML models can identify complex relationships between alloy composition, processing parameters, and mechanical properties. This enables faster and more accurate property predictions, accelerating the HEA design process. In HEA research, ML has been widely used for phase prediction (Chen et al., 2023; Ye et al., 2023; Zhang W. et al., 2023; He et al., 2024) and mechanical property estimation (Pan et al., 2025; Li S. et al., 2023; Yang et al., 2023; Jain et al., 2023).

For instance, Oñate et al. (2023) investigated HEA phase classification using four different ML models and found that the Random Forest model performed best, achieving an accuracy of 72.8%. Mandal et al. (2023) employed multiple ML algorithms incorporating atomic size difference, electronegativity difference, and three other parameters for phase and crystal structure classification, with decision tree and support vector machine (SVM) achieving a phase prediction accuracy of 93.84% and SVM attaining the highest classification accuracy of 84.32% for crystal structures. Zhao et al. (2024) utilized interpretable ML models combined with empirical descriptors to con-struct two-dimensional (2D) phase diagrams for HEAs. Compared to commonly used descriptors, their newly proposed descriptors improved prediction accuracy, reaching approximately 95% for distinguishing between crystalline and amorphous phases, as well as between BCC and FCC structures. Gao et al. (2024) applied ML combined with multi-objective optimization methods to design lightweight refractory HEAs within the Al-Nb-Ti-V-Zr-Cr-Mo-Hf system, achieving alloy densities of approximately 6.5 g/cm³, a maximum hardness of 593 HV, and a pitting potential up to 2.5 V. Ding et al. (2024) constructed a LightGBM-based predictive framework for refractory HEA yield strength, incorporating various feature selection methods, and achieved a coefficient of determination (R²) of 0.9605 with a root mean squared error (RMSE) of 111.99 MPa. Hoyos et al. (Ibarra Hoyos et al., 2024) developed an ML framework using Random Forest Regression (RFR) and Genetic Algorithm (GA), integrating physical properties to predict the yield strength and plastic strain of body-centered cubic (BCC) and BCC + B2 HEAs. In addition, Yasniy et al. (Yasniy et al., 2024) employed neural networks and boosted decision trees to model the thermal conductivity of epoxy-based composites with various fillers. Their approach achieved high prediction accuracy, with neural networks yielding errors as low as 0.2%–0.5% and boosted trees slightly higher (0.9%–1.5%), highlighting the reliability of ML techniques in simulating thermophysical properties of composite materials.

Predictive models using machine learning can significantly aid in the efficient design of alloys by exploring vast compositional spaces. Recent studies by Gupta et al. (Gupta K. et al., 2024; Gupta KK. et al., 2024) have shown how machine learning, combined with molecular dynamics, optimizes the composition of AlCoCrFeNi HEAs for improved properties like stiffness and high-temperature strength. Additionally, Mohanty et al. (Mohanty et al., 2023) applied machine learning to niobium alloys for high-temperature applications. These studies highlight how machine learning models can be used for alloy design, enabling faster and more accurate identification of optimal compositions.

In this study, we propose a stacking learning framework that integrates multiple ML models to enhance prediction accuracy and robustness for HEA mechanical properties. This approach combines the strengths of RF, SVM, and GB as base learners, while employing a meta learner to further optimize prediction performance. Additionally, SHapley Additive exPlanations (SHAP) analysis is incorporated to interpret the influence of key features on model predictions, offering deeper insights into the underlying factors governing HEA properties (Lundberg and Lee, 2017). The findings of this study provide a robust framework for data-driven HEA design, facilitating the accelerated discovery of high-performance alloys.

2 Methods

This study develops a stacking learning-based machine learning framework to predict the mechanical properties of high-entropy alloys (HEAs). The methodological framework is illustrated in Figure 1. The research workflow includes key stages such as dataset construction, feature selection, model optimization, and interpretability analysis to ensure the robustness and accuracy of predictions.

Figure 1

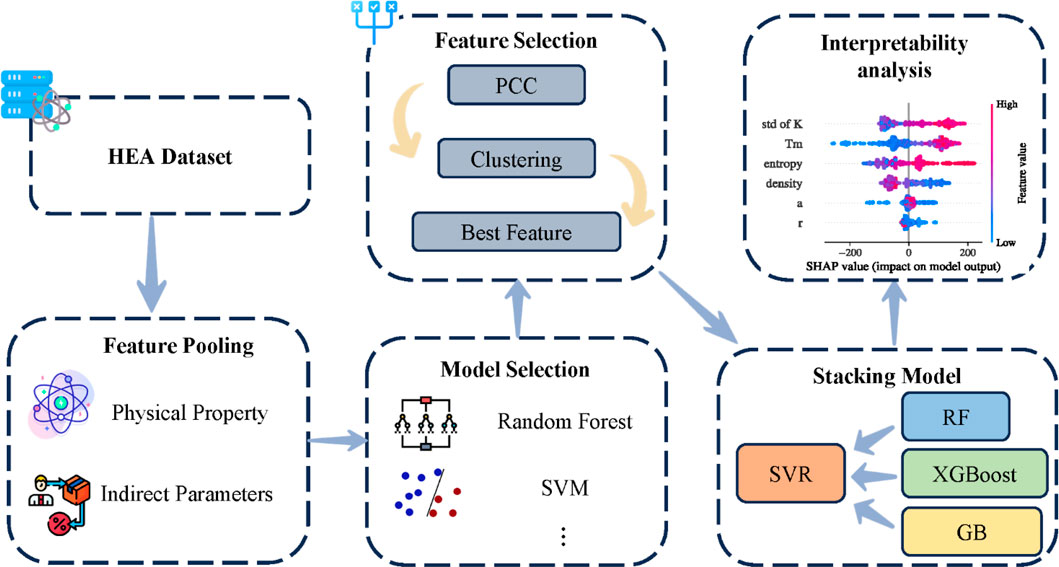
Figure 1. The overall framework of the proposed approach for high-entropy alloy property pre-diction. The workflow includes dataset preparation (HEA dataset), feature pooling (physical properties and indirect parameters), feature selection (PCC, clustering, and best features), model selection (Random Forest and SVM), interpretability analysis (SHAP), and the final stacking model—where Random Forest, Gradient Boosting, and XGBoost serve as base learners, and an SVR is used as the meta learner.

Stacking learning is an ensemble learning method that enhances predictive performance by integrating multiple base learners and introducing a meta learner. Unlike Bagging and Boosting, stacking learning employs a hierarchical structure. In the first layer, multiple base learners are independently trained and generate predictions based on input data. The second layer consists of a meta learner that aggregates the predictions from base learners to generate the final output. The diversity of base learners enables the system to capture complex interactions between features, while the meta learner further refines predictions, improving overall generalization and robustness.

The dataset used in this study is sourced from publicly available HEA databases and is supplemented with additional empirical parameters to enrich the feature space and improve model generalization. The final feature set includes fundamental physicochemical properties as well as derived parameters designed to capture complex relationships within material systems, providing comprehensive input information for the model.

For model selection, seven machine learning algorithms were evaluated, and Random Forest (RF), Extreme Gradient Boosting (XGBoost), and Gradient Boosting (GB) were ultimately chosen as base learners in the stacking framework. These models demonstrated superior predictive ability, robustness, and computational efficiency. Their combination effectively leverages their respective strengths, improving overall prediction accuracy.

Feature selection plays a crucial role in model performance. To optimize this process, a hierarchical clustering-model-driven hybrid feature selection strategy (HC-MDHFS) was proposed. Initially, hierarchical clustering was used to group highly correlated features, reducing feature redundancy and mitigating the adverse effects of multicollinearity. Subsequently, feature importance was dynamically assigned based on the performance of base learners across different feature subsets. This method automated and optimized feature selection, ensuring adaptability and accuracy for both yield strength and elongation prediction tasks.

After training the base learners, their predictions were used as inputs for training the meta learner. The selection of the meta learner was based on validation set performance, leading to the final choice of Support Vector Regression (SVR) as the meta learner. The final stacking model was constructed by integrating the tuned base learners with the optimized meta learner. This approach significantly enhanced the predictive power of the framework, demonstrating improved stability and accuracy com-pared to individual models.

To gain deeper insight into the decision-making process of the model, we employed the SHapley Additive exPlanations (SHAP) method for interpretability analysis. SHAP not only evaluates feature contributions in the base learners but also provides an overall assessment of feature importance in the stacked model. The results reveal the relative contributions of different features to yield strength and elongation predictions, helping to identify key factors influencing HEA mechanical properties. Further-more, SHAP analysis validates whether the learned feature patterns align with known principles in materials science, providing a data-driven foundation for optimizing feature engineering.

The proposed stacking learning framework integrates multiple machine learning models and employs a multi-level strategy involving feature selection, base model training, and meta learner optimization. This framework improves the accuracy and robustness of HEA mechanical property predictions. Overall, this study provides an efficient and reliable data-driven solution for materials property prediction, supporting the design and optimization of high-entropy alloys.

3 Results and discussions

3.1 Dataset and model selection

The dataset used was obtained from a publicly available HEA database (Li Z. et al., 2023), comprising 1,713 entries. Among these, 647 samples include yield strength data, and 486 samples contain elongation data, which are the primary focus of this study. To supplement the dataset, we integrated processing information from related studies (Li et al., 2024), resulting in a comprehensive dataset that includes compositional, phase, and processing features. Phase composition and processing methods significantly influence the mechanical properties of HEAs. For instance, HEAs with a face-centered cubic (FCC) structure typically exhibit high ductility but lower strength, whereas body-centered cubic (BCC) structures offer higher strength but reduced ductility (Nene, 2024). Processing techniques, such as laser melting deposition, can refine grain structures, leading to enhanced yield strength and elongation. Therefore, incorporating phase and processing information into predictive models is crucial for accurately assessing HEA mechanical performance (Song et al., 2024).

To capture the complex relationships between composition and mechanical properties, we introduced 17 empirical descriptors to enrich the feature space. For example, M. Calvo-Dahlborg et al. investigated the influence of mean atomic radius on HEAs, revealing that atomic radius and electron concentration jointly define phase regions, which can be utilized to predict HEA hardness, density, and phase composition (Calvo-Dahlborg et al., 2021). Chan-Sheng Wu et al. found that atomic size differences significantly affect the microstructure and mechanical properties of single FCC-phase HEAs, with larger atomic size variations increasing grain growth activation energy and lattice distortion (Wu et al., 2018). F.X. Zhang and Hong-Quan Song examined the effects of atomic size mismatch and chemical complexity on local lattice distortion in BCC solid solution alloys, concluding that atomic size mismatch is more influential and tends to overestimate lattice distortion in alloys containing four or more elements (Zhang and Song, 2022). X.D. Xu, S. Guo et al. analyzed the impact of mixing enthalpy and cooling rates on the phase formation of AlxCoCrCuFeNi HEAs, observing that increasing Al molar ratios shift mixing enthalpy from positive to negative, inducing phase transitions from FCC to BCC, while weak mixing enthalpy stabilizes solid solution phases. Their study also highlighted the combined effects of cooling rates and mixing enthalpy on phase formation (Xu et al., 2019). Numerous other studies have explored the impact of empirical parameters on HEAs (Zhao et al., 2022; Xjijocmr, 2015; Guo et al., 2011; Zhang et al., 2008). The calculation formulas for the features are presented in Supplementary Table S1.

To construct a stacking ensemble model for HEA property prediction, we systematically evaluated seven machine learning algorithms based on a balance between model diversity and predictive performance. The candidate models include:

• Ensemble Learning Models: XGBoost (Extreme Gradient Boosting), Random Forest (RF), and Gradient Boosting (GB). These models employ parallel and sequential decision tree mechanisms to capture nonlinear feature interactions, making them particularly suitable for high-dimensional, small-sample material datasets (Chen and Guestrin, 2016).

• Kernel-Based Model: Support Vector Regression (SVR), which utilizes radial basis function kernels to map data into higher-dimensional feature spaces, effectively handling complex nonlinear relationships between material properties and features (Smola and Schölkopf, 2004).

• Baseline Models: Decision Tree, K-Nearest Neighbors (KNN), and Ridge Regression, representing rule-based partitioning, local similarity fitting, and linear regularization approaches, respectively, to benchmark the advantages of ensemble models.

We evaluated the predictive performance of all candidate models using the coefficient of determination (R²) as the primary metric. As shown in Figure 2, XGBoost demonstrated superior performance in both tasks (yield strength: R² = 0.961; elongation: R² = 0.948), significantly outperforming other candidates. Random Forest (yield strength: R² = 0.918; elongation: R² = 0.879) and Gradient Boosting (yield strength: R² = 0.791; elongation: R² = 0.691) performed slightly lower than XGBoost in elongation prediction but exhibited strong noise suppression and model stability. Notably, SVR showed a distinct advantage in elongation prediction (R² = 0.717) but suffered from a significant drawback in yield strength prediction (R² = 0.557), limiting its overall applicability. The baseline models (Decision Tree/KNN/Ridge) demonstrated relatively poor performance (R² < 0.72) due to limited model capacity and susceptibility to overfitting.

Figure 2

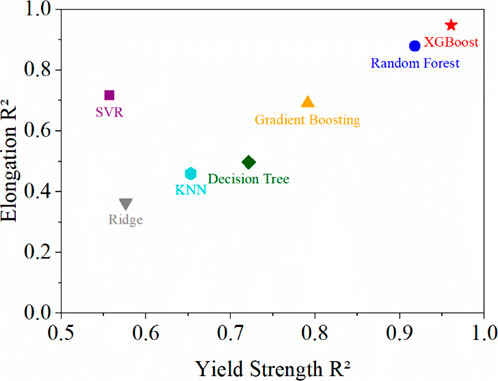
Figure 2. Performance comparison of various regression models (SVR, XGBoost, random forest, Gradient boosting, decision tree, KNN, and Ridge) for high-entropy alloy property prediction.

Key advantages of the selected ensemble models include:

• Robust Feature Selection: Tree-based models inherently assess feature importance, enabling adaptive selection of key physicochemical parameters.

• Noise Tolerance: Bagging/Boosting strategies reduce sensitivity to outliers through resampling, effectively addressing the composition-processing noise prevalent in HEA datasets (González et al., 2020).

• Multi-Scale Generalization: Ensemble models exhibit superior capability in de-coupling atomic-scale and macro-performance correlations.

Based on predictive accuracy, XGBoost, Random Forest, and Gradient Boosting were selected as base learners for the stacking framework.

3.2 Feature selection

In machine learning, feature selection is a critical step for improving model performance and interpretability. By eliminating redundant features and mitigating the risk of the curse of dimensionality, feature selection simplifies model complexity and enhances generalization ability. Traditional approaches often rely on manually selecting highly correlated features, such as identifying feature interdependencies using Pearson correlation coefficient matrices and retaining key variables based on domain knowledge (Guyon and AJJomlr, 2003; Gao et al., 2023; Zhang Y-F. et al., 2023). Existing studies commonly use correlation coefficient thresholds (e.g., >0.9) to directly remove redundant features (Gao et al., 2023) or perform subjective selection based on expert judgment (Chen et al., 2020). However, these methods have two key limitations: (1) manual selection is subject to human bias, potentially leading to the omission of important features or the retention of redundant ones; (2) such methods focus only on pairwise correlations, failing to optimize the feature set holistically.

To address these challenges, this study proposes a Hierarchical Clustering-Model Driven Hybrid Feature Selection (HC-MDHFS) strategy, which automatically groups highly correlated features using hierarchical clustering and dynamically assigns feature importance weights based on base learner performance, thereby automating and optimizing feature selection. This strategy consists of the following key steps:

3.2.1 Feature correlation analysis

In the feature selection process, it is first necessary to evaluate the correlations between different features. To achieve this, we calculated the Pearson correlation coefficient matrix for the 17 empirical parameters to measure the linear correlation be-tween features. The Pearson correlation coefficient is defined as shown in Equation 1:

$r=\frac{\sum \left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{\sum {\left(x_i-\overline{x}\right)}^2·\sum {\left(y_i-\overline{y}\right)}^2}}(1)$

where $r\in \left[-1,1\right]$ represents the degree of linear correlation between two variables. The closer the absolute value of is to 1, the stronger the correlation. When $r>0$, the two variables exhibit a positive correlation, meaning that an increase in one variable tends to be accompanied by an increase in the other. Conversely, when $r<0$, the two variables are negatively correlated. If $r\approx 0$, it indicates little to no linear relationship between the variables. The calculation results are shown in Figure 3. Notably, atomic size difference and lattice distortion exhibit a strong positive correlation ($r=0.95$), which is highly consistent with the solid solution lattice distortion theory of HEAs (Wang H. et al., 2024).

Figure 3

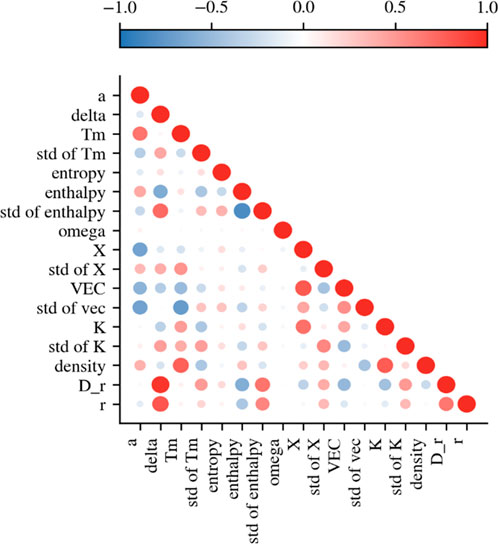
Figure 3. Correlation heatmap of the selected features (a, δ, Tm, std of Tm, entropy, enthalpy, std of enthalpy, ω, X, std of X, VEC, std of VEC, K, std of K, density, D_r, and r) in the high-entropy alloy dataset. The color scale ranges from −1 (blue) to +1 (red), representing negative and positive correlations, respectively.

Based on the feature correlation analysis, we further applied the Variance Inflation Factor (VIF) to quantify the degree of multicollinearity. The VIF is calculated as shown in Equation 2 (Belsley et al., 2005):

$VI{F}_j=\frac{1}{1-R_j^2}(2)$

where $R_j^2$ represents $x_j$ the coefficient of determination obtained by regressing feature on all other features. A higher VIF value indicates a stronger linear correlation between a given feature and the remaining features, meaning that multicollinearity is more severe. The average VIF value of the initial feature set was 18.6, far exceeding the commonly used threshold of 10, indicating a serious multicollinearity issue in the dataset. Therefore, feature selection was necessary to reduce redundancy and improve model stability and interpretability.

3.2.2 Hierarchical clustering-based feature grouping

To effectively group highly correlated features and reduce feature redundancy, this study employs hierarchical clustering to classify features into distinct groups. The clustering process consists of the following steps:

1. Distance Calculation: The Euclidean distance metric was used to quantify the similarity between features. As shown in Equation 3, the closer two features are in terms of distance, the more correlated they are:

$d_{xy}=1-\left|r_{xy}\right|(3)$

2. Clustering Method: Hierarchical clustering was performed using Ward’s minimum variance method and the distance between classes was calculated as shown in Equation 4 (Ward, 1963):

$D\left(A,B\right)=\frac{\left|A\right|\left|B\right|}{\left|A\right|+\left|B\right|}{‖{\overline{x}}_A-{\overline{x}}_B‖}^2(4)$

where, $\left|A\right|,\left|B\right|$ is the number of samples within the class, and ${\overline{x}}_A,{\overline{x}}_B$ is the class center. The Ward method is more robust to noise and generates more compact class clusters than the single-connection/full-connection method. A dendrogram was constructed to visualize the hierarchical clustering structure, as shown in Figure 4.

3. Cluster Grouping and Threshold Selection: A predefined threshold was applied to determine the optimal number of feature groups. Features within the same cluster exhibit high correlation, forming six distinct feature groups.

Figure 4

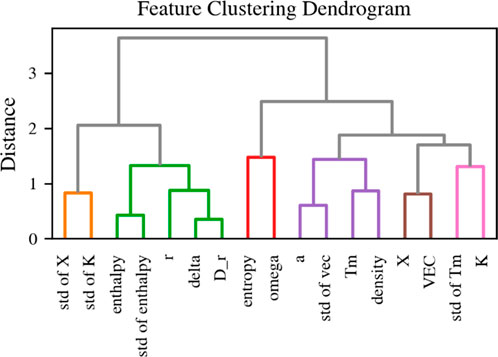
Figure 4. Hierarchical clustering dendrogram of the empirical parameters in the high-entropy alloy dataset.

The clustering results are summarized in Supplementary Table S2, showing the six feature groups obtained through this process. Each group contains highly correlated features, validating the effectiveness of hierarchical clustering in feature selection.

Hierarchical clustering improves feature selection by grouping correlated variables, minimizing redundancy, and retaining only the most informative descriptors for model training. This structured approach enables more effective handling of feature interdependencies.

3.2.3 Model-driven feature importance allocation

With the base learners determined, we conducted dynamic feature screening based on the feature importance of these three models in the Yield Strength and Elongation dataset. First, the weighted feature importance of each model is calculated to comprehensively measure the contribution of different features to the prediction task. The weight of the model is calculated as shown in Equation 5:

$w_m=\frac{R_m^2}{{\sum }_{m=1}^3{R}_m^2}\left(m=1,2,3\right)(5)$

where $R_m^2$ is the average coefficient of determination (R²) of the ten-fold cross-validation of the first model on the dataset, which is used to measure the predictive power of the model. This weight is used to weight and sum the feature importance of each model to calculate the combined importance of each feature, as shown in Equation 6:

$w_f={\displaystyle \sum _m}{w}_m{I}_{m,f}(6)$

Where $I_{m,f}$ is the feature importance score calculated by the model m for the feature f. Then, the combined importance of each feature group is calculated as shown in Equation 7:

$I_{G_i}=\frac{{\sum }_{f\in G_i}{W}_f}{\sum W_f}(7)$

Where $W_f$ represents the weighted importance of the feature f. $I_{G_i}$ reflects the relative importance of the feature group $G_i$ in the overall feature selection. Based on the value $I_{G_i}$, we dynamically allocate the number of features to be selected for each feature group. Assuming that the total number of features to be selected is K, then the number of features to be selected for a feature group $G_i$ is calculated as shown in Equation 8:

$N_{G_i}=round\left(I_{G_i}\times K\right)(8)$

where $round\left(\right)$ denotes rounding to the nearest integer. If the result of the calculation exceeds the maximum selectable number of feature groups, adjustments are made to ensure that the total number of features remains K.

3.2.4 Hierarchical clustering-based feature grouping

In order to further optimize the feature selection, we used grid search with three-fold cross-validation to evaluate the average performance of XGBoost, Random Forest, and Gradient Boosting while iterating over different total feature counts. For each total number of features K, we allocated the number of features per cluster proportionally based on the group-wise importance scores.

All possible combinations were then exhaustively searched, and the one that yielded the highest average R² was selected as the optimal feature subset.

Through the hierarchical clustering-model-driven hybrid feature screening strategy (HC-MDHFS), this study systematically evaluates the effect of different number of features on the prediction performance of Yield Strength and Elongation. Figures 5A, B show the correlation curves between the number of features and the model performance in the two tasks, respectively, revealing the optimization boundaries of feature selection.

• Yield strength prediction task

Figure 5

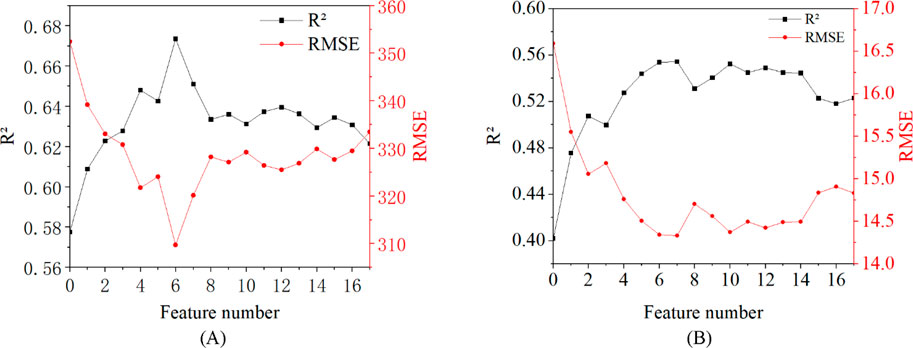
Figure 5. Correlation curves (R² and RMSE) between the number of selected features and the model performance for yield strength (YS) (A) and elongation (B), systematically evaluated under the hierarchical clustering–model-driven hybrid feature screening strategy (HC-MDHFS).

When the number of features is gradually increased from 0 to 6, the model performance significantly improves from 0.578 to 0.673, and the RMSE decreases from 352.42 MPa to 309.71 MPa. When the number of features exceeds 6, it starts to decrease ($R^2=0.621$ when $K=17$), and the RMSE rises to 333.50 MPa, which indicates that the introduction of the redundant features leads to overfitting. The optimal number of features is finally determined to be 6, at which time the model reaches a balance between accuracy ($R^2=0.673$) and complexity. The selected six features are: $a$, $\gamma$, $\rho$, $T_m$, ${\sigma }_K$ and $\Delta S$.

• Elongation prediction task

The elongation prediction is less sensitive to the number of features, but there is also a clear optimal point. When the number of features is 7, the peak value of 0.554 is reached, and the RMSE is 14.34%, which is 37.8% higher than the baseline. When the number of features is 7, it reaches a peak of 0.554, with an RMSE of 14.34%, which is 37.34% higher than the baseline ($R^2=0.402$ when $K=0$), The fluctuation range is less than 1%, which indicates that the model is more robust to the extra features, but in order to avoid the waste of computational resources, it is chosen as the optimal solution. The selected seven features are: ${\sigma }_{\Delta H}$, $X$, $D\_r$, $\rho$, $\Delta X$ and $\mathrm{\Omega }$.

3.3 Model training and optimization

After selecting XGBoost, Random Forest, and Gradient Boosting as base learners, we applied several training strategies to enhance model generalization and prediction accuracy.

First, to stabilize the data distribution, a logarithmic transformation (log (1 + y)) was applied to the target variables (Yield Strength and Elongation), reducing the impact of large numerical spans on model fitting. Additionally, to enhance prediction performance in high-value regions, a sample weighting strategy was introduced—samples above the 90th percentile were assigned a higher weight (weight = 2), while the remaining samples had a weight of 1. During training, ten-fold cross-validation (ten-fold CV) was employed for hyperparameter tuning, ensuring strong generalization ability. The fold-wise performance metrics are summarized in Supplementary Table S3.

With these optimization strategies, XGBoost, Random Forest, and Gradient Boosting were trained and optimized for both yield strength and elongation prediction tasks. The results were shown in Figures 6A, C. Specifically, for the yield strength dataset, Gradient Boosting achieved an R² of 0.824 on the training set and 0.716 on the test set; Random Forest scored 0.823 and 0.730, respectively; and XGBoost obtained 0.800 and 0.713. In the elongation dataset, Gradient Boosting performed exceptionally well, with R² values of 0.856 (training) and 0.719 (testing); Random Forest followed with 0.771 and 0.723; while XGBoost scored 0.752 and 0.672.

Figure 6

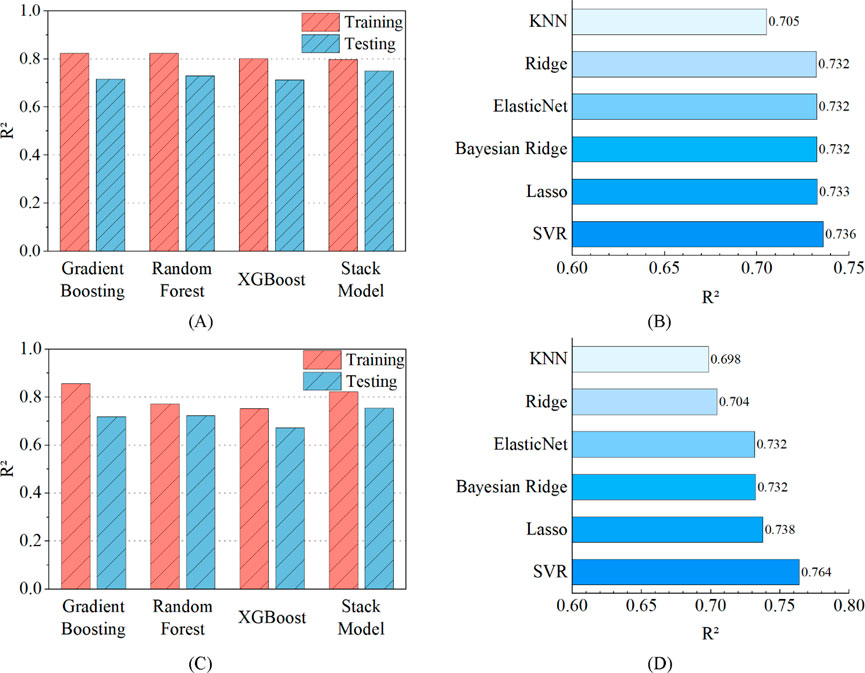
Figure 6. Performance evaluation of the ensemble learning framework for yield strength and elongation prediction: (A) Yield strength: Training and test R² values for the base learners and the stacked ensemble, (B) Yield strength: R² comparison among candidate meta learners, (C) Elongation: Training and test R² values for the base learners and the stacked ensemble, (D) Elongation: R² comparison among candidate meta learners.

These results indicate that all three models achieved high training accuracy, with Gradient Boosting showing particularly strong performance in the elongation prediction task, suggesting a well-fitted model. However, there was a slight decrease in R² values on the test set, indicating some degree of overfitting.

Notably, in yield strength prediction, XGBoost and Random Forest exhibited similar performance on the test set, but in the elongation task, XGBoost slightly lagged behind the other two models. This may indicate that XGBoost is less effective in capturing nonlinear relationships compared to Gradient Boosting, while Random Forest maintained stable performance across both datasets.

After training the base learners, we further trained the meta learner to fully leverage the predictions from the base learners and enhance the final predictive performance. To ensure the robustness of meta learner training and effectively prevent data leakage, a two-level cross-validation strategy was employed to generate meta-features.

In this strategy, each base learner underwent ten-fold cross-validation, where the training set was divided into ten subsets. Each time, nine subsets were used for training the base model, while the remaining subset was used for prediction. The predictions from all subsets were then concatenated and used as input meta-features for training the meta learner. This process ensured that every sample’s predicted value was generated from a model that had not seen it during training, fundamentally eliminating the risk of data leakage. Additionally, meta-features for the test set were directly generated by applying the base learners to the full test set, ensuring consistency in evaluation.

To optimize the performance of the meta learner, six regression models were evaluated: Ridge Regression, Support Vector Regression (SVR), ElasticNet, Bayesian Ridge, K-Nearest Neighbors (KNN), and Lasso Regression. A five-fold cross-validation procedure was conducted to select the optimal meta learner, and the performance of different meta learners in predicting yield strength and elongation was compared. The results, as shown in Figures 6B, D, indicate that different meta learners exhibited varying predictive capabilities across the two tasks.

In the yield strength prediction task, SVR (R² = 0.736) and Lasso regression (R² = 0.733) exhibited similar predictive capabilities, while ElasticNet regression (R² = 0.732) also showed certain advantages due to its combination of L1/L2 regularization, which helps suppress multicollinearity. Although Lasso benefits from L1 regularization, its aggressive feature selection process may lead to the loss of some critical information, making SVR the preferred choice.

In the elongation prediction task, SVR achieved the best performance (R² = 0.764), as its radial basis function (RBF) kernel effectively captured nonlinear characteristics and constructed optimized decision boundaries in high-dimensional space. This performance was superior to that of linear models such as Ridge regression (R² = 0.738), which demonstrated stronger adaptability.

Considering both prediction accuracy and model stability, SVR was ultimately selected as the optimal meta learner for both yield strength and elongation prediction tasks.

After determining the optimal meta learner, we constructed a stacked regression model, incorporating XGBoost, Random Forest, and Gradient Boosting as base learners. The optimized meta learner was employed to explore relationships in the feature space and infer complex nonlinear dependencies.

As shown in Figures 6A, C, although the performance of individual base learners was not optimal, stacking learning achieved enhanced generalization. For example, in yield strength prediction, the ensemble model achieved an R² of 0.798, outperforming Gradient Boosting (0.824) and Random Forest (0.823) in training, but demonstrating superior test performance compared to all base learners. The test set R² for base learners was 0.716 (Gradient Boosting), 0.730 (Random Forest), and 0.713 (XGBoost).

Similarly, in the elongation prediction task, the stacked model exhibited a training R² of 0.822 and a test R² of 0.755, surpassing the individual base learners, whose test set R² values were 0.719 (Gradient Boosting), 0.723 (Random Forest), and 0.672 (XGBoost).

To further evaluate prediction performance from the perspective of relative error, Supplementary Table S4 summarizes the relative errors of each model on the test set. Compared to the base learners, the stacked model reduced the relative error by approximately 3% in the yield strength prediction task and 4% in the elongation prediction task, indicating its superior predictive accuracy and generalization capability.

These results indicate that although the ensemble model’s training R² was slightly lower than that of some base learners, its test set R² was consistently higher, suggesting improved generalization. By effectively integrating the advantages of multiple base learners, the stacked learning approach balanced feature representation and model interpretability, mitigating overfitting risks while leveraging diverse learning strategies. This validates the superiority of stacking learning in high-performance alloy mechanical property prediction.

3.4 Interpretability analysis

Following the training and evaluation of the stacking model, this study further employs SHAP to explain the model’s predictions and quantify the influence of empirical input feature. Derived from cooperative game theory, SHAP enables precise attribution of each feature’s impact on individual predictions, offering insight into the model’s internal logic.

For the yield strength prediction task, Figure 7A illustrates the average SHAP values of the base learners (XGBoost, Random Forest, and Gradient Boosting). The results indicate that the standard deviation of bulk modulus (std of K), entropy, and average melting temperature (Tm) are the three most influential features in the prediction. Among them, the standard deviation of bulk modulus exhibits the highest SHAP importance value, highlighting its crucial role in the model’s decision-making process. Bulk modulus reflects a material’s resistance to volumetric deformation, and its standard deviation measures the compositional variation among alloying elements. A greater deviation often suggests localized stress heterogeneity, which can hinder dislocation motion by increasing the energy barrier, ultimately leading to an increase in yield strength (Wang T. et al., 2024). This is because dislocations must bypass regions of varying atomic environments, where lattice distortions create resistance to their movement. As a result, more external stress is needed to initiate plastic deformation. Entropy, the second most important feature, is associated with the degree of elemental mixing; a higher entropy value typically promotes the formation of stable solid solution structures, reducing the risk of phase separation and thereby enhancing yield strength (Winkens et al., 2023). This stabilization arises from the increased configurational entropy, which lowers the Gibbs free energy of the solid solution. As a result, it suppresses the formation of brittle intermetallic phases and maintains a more uniform microstructure conducive to strength. Lastly, average melting temperature reflects atomic bonding strength—higher melting points generally indicate stronger interatomic interactions, increasing material rigidity and deformation resistance (Miracle et al., 2017).

Figure 7

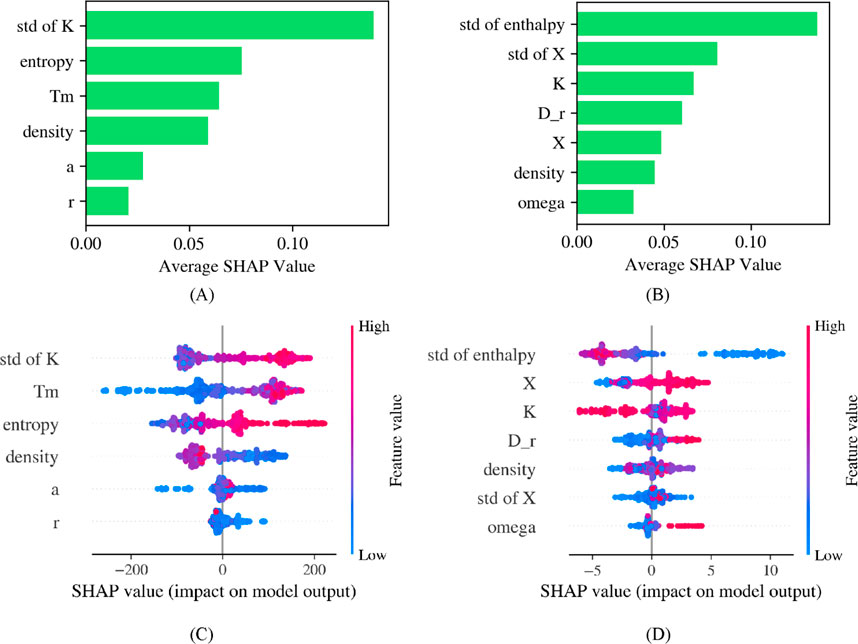
Figure 7. SHAP analysis of the base learners and the stacking model for yield strength and elongation: (A) Base learners SHAP values for yield strength, (B) Base learners SHAP values for elongation, (C) Stacking-model SHAP values (with kernel density) for yield strength, (D) Stacking-model SHAP values (with kernel density) for elongation.

Figure 7C presents the SHAP analysis results for the stacking model, along with a kernel density estimation of feature contributions. While standard deviation of bulk modulus, entropy, and average melting temperature remain the dominant factors influencing yield strength predictions, the stacking model exhibits a more balanced feature contribution distribution. Notably, a higher standard deviation of bulk modulus corresponds to a higher SHAP value, confirming its significant positive impact on yield strength. Meanwhile, entropy’s SHAP influence is more evenly distributed, likely due to the stacking model’s ability to smooth feature contributions across multiple base learners. The SHAP distribution of average melting temperature appears more compact, indicating that in the stacking learning process, this feature provides a stable and effective capture of the nonlinear relationship between melting temperature and yield strength.

For the elongation prediction task, Figure 7B illustrates the average SHAP values of the base learners, revealing that the standard deviation of enthalpy (std of enthalpy), standard deviation of electronegativity (std of X), and average bulk modulus (K) contribute the most to the predictions. Among these, the standard deviation of enthalpy exhibits the highest SHAP importance, suggesting that fluctuations in enthalpy significantly impact phase stability and localized stress distribution, which in turn affect elongation (Jin et al., 2018). Greater enthalpy fluctuations can destabilize solid solution phases and promote the formation of second phases or defects, leading to strain localization during deformation and thus reducing ductility. The standard deviation of electronegativity reflects differences in bond strength among alloying elements; such variations influence dislocation motion and atomic diffusion, thereby increasing resistance to plastic deformation and ultimately reducing elongation (Bent, 1961). Large electronegativity differences can induce chemical short-range ordering and enhance lattice friction, which obstructs dislocation glide and limits the material’s ability to deform uniformly. Meanwhile, average bulk modulus represents a material’s resistance to volumetric deformation—higher values correspond to stronger interatomic interactions, resulting in increased material rigidity and reduced dislocation mobility, which can lower elongation (Temesi et al., 2024). Conversely, materials with lower bulk modulus tend to exhibit higher plastic deformation capacity, leading to greater elongation.

Figure 7D presents the SHAP analysis results for the stacking model, demonstrating some adjustments in feature contribution patterns compared to the base learners. Specifically, higher standard deviation of enthalpy values correspond to lower SHAP values, indicating that an increase in enthalpy fluctuations may lead to reduced elongation. The SHAP values of standard deviation of electronegativity are more concentrated, suggesting that the stacking model effectively stabilizes the impact of this feature on predictions. Similarly, the SHAP values of average bulk modulus exhibit a more compact distribution, implying a more stable representation of the relationship between bulk modulus and elongation in the stacking model.

The SHAP analyses of both the base learners and the stacking model show consistent feature importance rankings, confirming that the standard deviation of enthalpy, standard deviation of electronegativity, and average bulk modulus are the most influential features for elongation prediction. However, the stacking model’s SHAP results are more balanced, with kernel density estimation further refining the distribution of feature contributions, enhancing the model’s stability and generalization ability. This indicates that stacking learning not only preserves the base learners’ sensitivity to key features but also optimizes feature contribution distribution, leading to a more reliable decision-making process in the final model.

Based on the SHAP-derived feature importance analysis, we propose the following composition design strategies to guide the optimization of high-entropy alloys. First, to achieve a balance between local stress heterogeneity and overall plasticity, it is advisable to select elemental combinations with moderate variation in bulk modulus, particularly by combining transition metals with refractory elements. Second, the phase stability of solid solutions can be enhanced by coordinating configurational entropy and mixing enthalpy, which involves increasing the number of principal elements to raise entropy while avoiding excessive incorporation of elements with highly negative mixing enthalpy that may promote intermetallic formation. Third, to suppress chemical ordering and improve ductility, elements with similar electronegativity, such as Fe, Co., and Ni, should be prioritized. These data-driven strategies provide actionable guidance for HEA composition design and can be further validated through high-throughput computational approaches such as CALPHAD, combined with experimental evaluation.

4 Conclusion

We introduce a novel Hierarchical Clustering Model-Driven Hybrid Feature Selection (HC-MDHFS) strategy that first groups highly correlated descriptors and then allocates importance weights according to predictive power. This method mitigates multicollinearity in high-dimensional HEA datasets while preserving the most relevant parameters for yield strength and elongation, offering a clear methodological advance over conventional feature-pruning techniques.

By combining Extreme Gradient Boosting, Random Forest and Gradient Boosting as base learners within a two level stacking framework and using Support Vector Regression as the meta learner, our ensemble achieves superior generalization on unseen data. Specifically, test set coefficients of determination reach 0.749 for yield strength and 0.755 for elongation.

To reveal the physical basis of these predictions, we apply Shapley Additive ExPlanations to each model component. Our findings show that the standard deviation of bulk modulus, configurational entropy and average melting temperature most strongly influence yield strength, whereas variations in mixing enthalpy, electronegativity variance and bulk modulus predominantly govern elongation. These results both confirm established metallurgical principles and uncover new composition-property relationships that can directly inform future alloy design efforts.

In summary, this work establishes a rigorously validated interpretable ensemble modeling pipeline for HEA mechanical-property prediction. The integration of automatic feature grouping, robust model stacking and game-theoretic interpretability lays a strong foundation for data driven alloy design and opens the door to subsequent inverse design studies and experimental validation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

SZ: Writing – original draft, Software, Conceptualization, Data curation. ZL: Writing – review and editing, Formal Analysis, Conceptualization. CY: Methodology, Writing – review and editing. ZZ: Writing – review and editing. TL: Writing – review and editing. JY: Writing – review and editing. RC: Writing – review and editing, Funding acquisition. YG: Writing – review and editing, Funding acquisition, Project administration.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors acknowledge the financial support from the UK Research and Innovation (UKRI) through the REWIRE Innovation and Knowledge Centre (Grant No. EP/Z531091/1), the National Natural Science Foundation of China (Grant Nos. 62174122, 52302046, U2241244, and 62361166628), the Guangdong Basic and Applied Basic Research Foundation (Grant Nos. 2024A1515011764, 2022A1515110149 and 2024A1515010383), the Knowledge Innovation Pro-gram of Wuhan-Shuguang Project (Grant No. 2023010201020262), the Natural Science Foundation of Jiangsu Province (Grant No. BK20230268), the Open Fund of Hubei Key Laboratory of Electronic Manufacturing and Packaging Integration (Wuhan University) (Grant No. EMPI2024020). The numerical calculations in this work were conducted on the supercomputing system in the Super-computing Center of Wuhan University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2025.1601874/full#supplementary-material

References

Belsley, D. A., Kuh, E., and Welsch, R. E. (2005). Regression diagnostics: identifying influential data and sources of collinearity. John Wiley and Sons.

Google Scholar

Bent, HAJCR (1961). An appraisal of valence-bond structures and hybridization in compounds of the first-row elements. Elements 61 (3), 275–311. doi:10.1021/cr60211a005

CrossRef Full Text | Google Scholar

Calvo-Dahlborg, M., Mehraban, S., Lavery, N., Brown, S., Cornide, J., Cullen, J., et al. (2021). Prediction of phase, hardness and density of high entropy alloys based on their electronic structure and average radius. Electron. Struct. Aver. Radius 865, 158799. doi:10.1016/j.jallcom.2021.158799

CrossRef Full Text | Google Scholar

Cantor, B., Chang, I. T., Knight, P., and Vincent Ajms, A. E. (2004). Microstructural development in equiatomic multicomponent alloys. 375:213–218. doi:10.1016/j.msea.2003.10.257

CrossRef Full Text | Google Scholar

Chen, C., Zhang, Q., Yu, B., Yu, Z., Lawrence, P. J., Ma, Q., et al. (2020). Improving protein-protein interactions prediction accuracy using xgboost feature selection and stacked ensemble classifier. Comput. Biol. Med. 123, 103899. doi:10.1016/j.compbiomed.2020.103899

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Zhou, H., Long, W., Wang, G., and Ren, JJSCTS (2023). Phase prediction for high-entropy alloys using generative adversarial network and active learning based on small datasets. Sci. China Technol. Sci. 66 (12), 3615–3627. doi:10.1007/s11431-023-2399-2

CrossRef Full Text | Google Scholar

T. Chen, and C. Guestrin (2016). “Xgboost: a scalable tree boosting system,” Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining.

Google Scholar

Ding, S., Wang, W., Zhang, Y., Ren, W., Weng, X., Chen, JJIJ. R. M., et al. (2024). A yield strength prediction framework for refractory high-entropy alloys based on machine learning. Mach. Learn. 125, 106884. doi:10.1016/j.ijrmhm.2024.106884

CrossRef Full Text | Google Scholar

Gao, M. C., and Alman, DEJE (2013). Searching for next single-phase high-entropy alloy compositions. Entropy (Basel). 15 (10), 4504–4519. doi:10.3390/e15104504

CrossRef Full Text | Google Scholar

Gao, T., Gao, J., Yang, S., and Zhang, L. J. C. M. (2024). Data-driven design of novel lightweight refractory high-entropy alloys with superb hardness and corrosion resistance. npj Comput. Mat. 10 (1), 256. doi:10.1038/s41524-024-01457-6

CrossRef Full Text | Google Scholar

Gao, Z., Zhao, F., Gao, S., and Xia, TJMTC (2023). Machine learning prediction of hardness in solid solution high entropy alloys. Entropy Alloys 37, 107102. doi:10.1016/j.mtcomm.2023.107102

CrossRef Full Text | Google Scholar

González, S., García, S., Del Ser, J., Rokach, L., and Herrera, FJIF (2020). A practical tutorial on bagging and boosting based ensembles for machine learning: algorithms. Softw. Tools, Perform. Study, Pract. Perspect. Oppor. 64, 205–237. doi:10.1016/j.inffus.2020.07.007

CrossRef Full Text | Google Scholar

Guo, Q., Hou, H., Wang, K., Li, M., Liaw, P. K., and Zhao, YJNCM (2023). Coalescence of Al0.3CoCrFeNi polycrystalline high-entropy alloy in hot-pressed sintering: a molecular dynamics and phase-field study. A Mol. Dyn. Phase-Field Study 9 (1), 185. doi:10.1038/s41524-023-01139-9

CrossRef Full Text | Google Scholar

Guo, S., Ng, C., Lu, J., and Liu, C. J. J. (2011). Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 109 (10). doi:10.1063/1.3587228

CrossRef Full Text | Google Scholar

Gupta, K., Barman, S., Dey, S., Naskar, S., and Mukhopadhyay, TJSR (2024a). On exploiting nonparametric kernel-based probabilistic machine learning over the large compositional space of high entropy alloys for optimal nanoscale ballistics. Nanoscale Ballist. 14 (1), 16795. doi:10.1038/s41598-024-62759-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, K. K., Barman, S., Dey, S., and Mukhopadhyay, TJMLS (2024b). Explainable machine learning assisted molecular-level insights for enhanced specific stiffness exploiting the large compositional space of AlCoCrFeNi high entropy alloys. Entropy Alloys 5 (2), 025082. doi:10.1088/2632-2153/ad55a4

CrossRef Full Text | Google Scholar

Guyon, I., and Ajjomlr, E. (2003). An introduction to variable and feature selection, 1157–1182.

Google Scholar

He, Z., Zhang, H., Cheng, H., Ge, M., Si, T., Che, L., et al. (2024). Machine learning guided BCC or FCC phase prediction in high entropy alloys. Entropy Alloys 29, 3477–3486. doi:10.1016/j.jmrt.2024.01.257

CrossRef Full Text | Google Scholar

Ibarra Hoyos, D., Simmons, Q., and Poon, J. J. M. (2024). Predicting yield strength and plastic elongation in body-centered cubic high-entropy alloys. Entropy Alloys 17 (17), 4422. doi:10.3390/ma17174422

PubMed Abstract | CrossRef Full Text | Google Scholar

Jain, R., Lee, U., Samal, S., and Park, N. J. J. A. (2023). Machine-learning-guided phase identification and hardness prediction of Al-Co-Cr-Fe-Mn-Nb-Ni-V containing high entropy alloys. J. Alloys Compd. 956, 170193. doi:10.1016/j.jallcom.2023.170193

CrossRef Full Text | Google Scholar

Jin, X., Zhou, Y., Zhang, L., Du, X., and Li, B. J. M. (2018). A new pseudo binary strategy to design eutectic high entropy alloys using mixing enthalpy and valence electron concentration. Mat. Des. 143, 49–55. doi:10.1016/j.matdes.2018.01.057

CrossRef Full Text | Google Scholar

Lee, C., Maresca, F., Feng, R., Chou, Y., Ungar, T., Widom, M., et al. (2021). Strength can be controlled by edge dislocations in refractory high-entropy alloys. Entropy Alloys 12 (1), 5474. doi:10.1038/s41467-021-25807-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Li, S., Liu, D., Yang, J., and Zhang, M. J. J. A. (2023a). Hardness prediction of high entropy alloys with periodic table representation of composition, processing, structure and physical parameters. Struct. Phys. Param. 967, 171735. doi:10.1016/j.jallcom.2023.171735

CrossRef Full Text | Google Scholar

Li, Z., Li, S., and Birbilis, NJMTC (2024). A machine learning-driven framework for the property prediction and generative design of multiple principal element alloys. Mat. Today Commun. 38, 107940. doi:10.1016/j.mtcomm.2023.107940

CrossRef Full Text | Google Scholar

Li, Z., Zeng, Z., Tan, R., Taheri, M., and Birbilis, N. (2023b). A database of mechanical properties for multi principal element alloys. 47:101068. doi:10.1016/j.cdc.2023.101068

CrossRef Full Text | Google Scholar

Liu, D., Yu, Q., Kabra, S., Jiang, M., Forna-Kreutzer, P., Zhang, R., et al. (2022). Exceptional fracture toughness of crconi-based medium-and high-entropy alloys at 20 kelvin. Sci. (1979). 378 (6623), 978–983. doi:10.1126/science.abp8070

PubMed Abstract | CrossRef Full Text | Google Scholar

Lundberg, S. M., and Lee, S.-I. J. A. (2017). A unified approach to interpreting model predictions, 30.

Google Scholar

Mandal, P., Choudhury, A., Mallick, A. B., Ghosh, M. J. M., and International, M. (2023). Phase prediction in high entropy alloys by various machine learning modules using thermodynamic and configurational parameters. Mater. Mat. Int. 29 (1), 38–52. doi:10.1007/s12540-022-01220-w

CrossRef Full Text | Google Scholar

Maruschak, P., and Maruschak, O. J. M. (2024). Methods for evaluating fracture patterns of polycrystalline materials based on the parameter analysis of fatigue striations: a review. A Rev. 13, 102989. doi:10.1016/j.mex.2024.102989

PubMed Abstract | CrossRef Full Text | Google Scholar

Miracle, D. B., and Onjam, S. (2017). A critical review of high entropy alloys and related concepts. 122:448–511.

Google Scholar

Mohanty, T., Chandran, K., and Sparks, TDJAML (2023). Machine learning guided optimal composition selection of niobium alloys for high temperature applications. Apl. Mach. Learn. 1 (3). doi:10.1063/5.0129528

CrossRef Full Text | Google Scholar

Nene, S. S. (2024). Microstructure and mechanical properties of high entropy alloys. High entropy alloys: a machine-generated literature overview. Springer, 99–175.

Google Scholar

Oñate, A., Sanhueza, J. P., Zegpi, D., Tuninetti, V., Ramirez, J., Medina, C., et al. (2023). Supervised machine learning-based multi-class phase prediction in high-entropy alloys using robust databases. J. Alloys Compd. 962, 171224. doi:10.1016/j.jallcom.2023.171224

CrossRef Full Text | Google Scholar

Pan, H., Zheng, M., Li, X., and Zhao, S. J. J. M. I. (2025). Improved hardness prediction for reduced-activation high-entropy alloys by incorporating symbolic regression and domain adaptation on small datasets. J. Mat. Inf. 5 (1), N/A. doi:10.20517/jmi.2024.71

CrossRef Full Text | Google Scholar

Pickering, E., and Jones, NJIMR (2016). High-entropy alloys: a critical assessment of their founding principles and future prospects. Int. Mat. Rev. 61 (3), 183–202. doi:10.1080/09506608.2016.1180020

CrossRef Full Text | Google Scholar

Smola, A. J., and Schölkopf, B. J. S. (2004). Computing. A tutorial on support vector regression. 14:199–222.

CrossRef Full Text | Google Scholar

Song, M., Ma, B., Huang, H., Liu, L., Guo, R., Yin, Y., et al. (2024). A novel Ni40co18cr18fe14al5ti5 high entropy alloy with superior mechanical properties and broad printing window via selective laser melting. Mat. Des. 239, 112754. doi:10.1016/j.matdes.2024.112754

CrossRef Full Text | Google Scholar

Temesi, O. K., Varga, L. K., Chinh, N. Q., and Vitos, L. J. C. (2024). Ductility index for refractory high entropy alloys. Entropy Alloys 14 (10), 838. doi:10.3390/cryst14100838

CrossRef Full Text | Google Scholar

Wang, H., Yang, P., Zhao, W., Ma, S., Hou, J., He, Q., et al. (2024b). Lattice distortion enabling enhanced strength and plasticity in high entropy intermetallic alloy. Nat. Commun. 15 (1), 6782. doi:10.1038/s41467-024-51204-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., Guo, J., Chen, W., and Tian, YJMTC (2024a). Molecular dynamics simulations of tensile properties for fenicrcocu high-entropy alloy. Mat. Today Commun. 38, 108187. doi:10.1016/j.mtcomm.2024.108187

CrossRef Full Text | Google Scholar

Wang, T., Li, J., Wang, M., Li, C., Su, Y., Xu, S., et al. (2024c). Unraveling dislocation-based strengthening in refractory multi-principal element alloys. Alloys 10 (1), 143. doi:10.1038/s41524-024-01330-6

CrossRef Full Text | Google Scholar

Ward, Jr JHJJ. A. (1963). Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 58 (301), 236–244. doi:10.1080/01621459.1963.10500845

CrossRef Full Text | Google Scholar

Winkens, G., Kauffmann, A., Herrmann, J., Czerny, A. K., Obert, S., Seils, S., et al. (2023). The influence of lattice misfit on screw and edge dislocation-controlled solid solution strengthening in Mo-Ti alloys. Commun. Mat. 4 (1), 26. doi:10.1038/s43246-023-00353-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, C.-S., Tsai, P.-H., Kuo, C.-M., and Tsai, C.-W. J. E. (2018). Effect of atomic size difference on the microstructure and mechanical properties of high-entropy alloys. Alloys 20 (12), 967. doi:10.3390/e20120967

PubMed Abstract | CrossRef Full Text | Google Scholar

XjijoCMR, Ji (2015). Relative effect of electronegativity on formation of high entropy. Alloys 28 (4), 229–233. doi:10.1179/1743133615Y.0000000004

CrossRef Full Text | Google Scholar

Xu, X., Guo, S., Nieh, T., Liu, C., Hirata, A., and Chen, M. J. M. (2019). Effects of mixing enthalpy and cooling rate on phase formation of AlxCoCrCuFeNi high-entropy alloys. Entropy Alloys 6, 100292. doi:10.1016/j.mtla.2019.100292

CrossRef Full Text | Google Scholar

Yang, Z., Li, S., Li, S., Yang, J., and Liu, DJCMS (2023). A two-step data augmentation method based on generative adversarial network for hardness prediction of high entropy alloy. Comput. Mat. Sci. 220, 112064. doi:10.1016/j.commatsci.2023.112064

CrossRef Full Text | Google Scholar

Yasniy, O., Mytnyk, M., Maruschak, P., Mykytyshyn, A., and Didych, I. J. A. (2024). Machine learning methods as applied to modelling thermal conductivity of epoxy-based composites with different fillers for aircraft. 28(2):64–71. doi:10.3846/aviation.2024.21472

CrossRef Full Text | Google Scholar

Ye, Y., Li, Y., Ouyang, R., Zhang, Z., Tang, Y., and Bai, SJCMS (2023). Improving machine learning based phase and hardness prediction of high-entropy alloys by using Gaussian noise augmented data. Comput. Mat. Sci. 223, 112140. doi:10.1016/j.commatsci.2023.112140

CrossRef Full Text | Google Scholar

Yeh, J. W., Chen, S. K., Lin, S. J., Gan, J. Y., Chin, T. S., Shun, T. T., et al. (2004). Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mat. 6 (5), 299–303. doi:10.1002/adem.200300567

CrossRef Full Text | Google Scholar

Zhang, F., and Song, H.-QJMTC (2022). Effect of atomic size mismatch and chemical complexity on the local lattice distortion of bcc solid solution alloys. Mat. Today Commun. 33, 104367. doi:10.1016/j.mtcomm.2022.104367

CrossRef Full Text | Google Scholar

Zhang, W., Li, P., Wang, L., Wan, F., Wu, J., and Yong, LJMTC (2023a). Explaining of prediction accuracy on phase selection of amorphous alloys and high entropy alloys using support vector machines in machine learning. Mach. Learn. 35, 105694. doi:10.1016/j.mtcomm.2023.105694

CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, Y. J., Lin, J. P., Chen, G. L., and Pkjaem, L. (2008). Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mat. 10 (6), 534–538. doi:10.1002/adem.200700240

CrossRef Full Text | Google Scholar

Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2014). Microstructures and properties of high-entropy alloys. Alloys 61, 1–93. doi:10.1016/j.pmatsci.2013.10.001

CrossRef Full Text | Google Scholar

Zhang, Y.-F., Ren, W., Wang, W.-L., Li, N., Zhang, Y.-X., Li, X.-M., et al. (2023b). Interpretable hardness prediction of high-entropy alloys through ensemble learning. J. Alloys Compd. 945, 169329. doi:10.1016/j.jallcom.2023.169329

CrossRef Full Text | Google Scholar

Zhao, S., Yuan, R., Liao, W., Zhao, Y., Wang, J., Li, J., et al. (2024). Descriptors for phase prediction of high entropy alloys using interpretable machine learning. Mach. Learn. 12 (5), 2807–2819. doi:10.1039/d3ta06402f

CrossRef Full Text | Google Scholar

Zhao, X., Li, S., Jiang, J., Bai, J., Xie, H., Pan, H., et al. (2022). Polytypic omega/omega-like transformation in a refractory high-entropy alloy. Acta Mat. 238, 118207. doi:10.1016/j.actamat.2022.118207

CrossRef Full Text | Google Scholar