Application of New Iterative Method to Time Fractional Whitham–Broer–Kaup Equations

This article presents the fractional Laplace transform with the help of new iterative method (NIM) is extended for an estimated solution of coupled system of fractional order PDEs. The time fractional Whitham–Broer–Kaup system is taken as a test example where derivatives are given in the Caputo sense. Numerical results found by the proposed method are compared with that of ADM, VIM, and OHAM. Numerical consequences display that the proposed method is reliable and operative for solution of fractional order coupled system of PDEs. The proposed method shows better accuracy in even two iterations compared to the methods given above.

Introduction

As we know that many technical and engineering issues that arises in day-by-day existence are modeled via mathematical tools form fractional calculus (FC), i.e., fractional calculus can be used to simulate various real phenomena involving long memory, e.g., using fractional derivative, one can model HIV/AIDS model based on the effect of screening of unaware infectives [1]. Maximum problems that arise are non-linear, and it is not usually probable to locate systematic results of such problems since some researchers introduced new approaches for finding the exact solution of FPDEs [2]. However, these methods also have some drawbacks, and we cannot use it for any type of problems. To fulfill these need, researchers introduced many semi analytical techniques such as HPM [3], HPTM [4], HAM [5], FDM [6], RPSM [7], etc.

NIM was introduced by Daftardar-Gejji and Jafari in 2006 and is also known as the DJ method for the solution of non-linear equations. This method is the modification of ADM in which the complex Adomian polynomials are replaced by Jafari polynomials. Therefore, we have no need to compute tedious Adomian's polynomial in each iteration.

In this presentation, we have extended the applications of the DJ method to a solution of coupled WBK equations of fractional order using the fractional Laplace Transform. Using the Laplace transform for fractional PDEs is effortless compared to the Riemann Liouvelle integral operator for fractional PDEs as well as a system of fractional PDEs.

The fractional-order WBK equations describe the propagation of shallow water waves [8] with different dispersion relations. The WBK equations are of the form:

$\begin{array}{c}{D}_t^{\alpha }u+u{u}_x+v_x+b{u}_{xx}=0\\ D_t^{\alpha }v+{(uv)}_x+a{u}_{xxx}-b{v}_{xx}=0,\end{array}$

where u(x, t) denotes the horizontal velocity, v(x, t) is the height that deviates from the equilibrium position, a, b are real constants that are represented in different diffusion powers, and $D_t^{\alpha }$0 < α ≤ 1 is the Caputo derivative operator. For α = 1, we get the usual WBK equations. It is also essential to show that when a = 1 and b = 0, we have fractional order modified Boussinesq (MB) equation, and when a = 0, $b{=}^1{/}_2$, we get the fractional order approximate long wave (ALW) equation. These equations took the attention of many researchers in recent decades [9–11].

The present paper is divided into five sections. The Fundamental Theory of Proposed Method section is devoted to the analysis of the DJ method as well as the implementation of the Laplace transform for fractional PDEs are given. In the Application of Laplace Transform with DJ method to Fractional Whitham-Broer-Kaup Equations section, the application of Laplace transform to FPDEs are given. In the Results and Discussion section, the results of the proposed method are compared with VIM, ADM, and OHAM solutions for time-fractional WBK, time fractional MB, and time-fractional ALW equations, while in the Conclusion section, the conclusion of the work is given.

Fundamental Theory of Proposed Method

New Iterative Method [12–16]

Daftardar-Gejji and Jafari consider the following equation [12]:

Consider the equations of the form:

$\begin{array}{ll}{\nu }_i=f_i+{\varsigma }_i({\nu }_1,{\nu }_2)+{\xi }_i({\nu }_1,{\nu }_2),i=1,2.& (1)\end{array}$

wheref_i are known functions, ς_i, ξ_i are linear and non-linear functions of ν_i. Assuming that equation (1) have a solution of the series form:

$\begin{array}{ll}{\nu }_i={\displaystyle \sum _{j=0}^{\infty }}{\nu }_{i,j},i=1,2.& (2)\end{array}$

Since ς_i is linear, so we write it as:

$\begin{array}{ll}{\varsigma }_i\left({\displaystyle \sum _{j=0}^{\infty }}({\nu }_{1,j},{\nu }_{2,j})\right)={\displaystyle \sum _{j=0}^{\infty }}{\varsigma }_i({\nu }_{1,j},{\nu }_{2,j}),& (3)\end{array}$

Decomposition of non-linear operators is as follows:

$\begin{array}{l}{\xi }_i\left({\displaystyle \sum _{j=0}^{\infty }}{\nu }_{i,j}\right)={\xi }_i({\nu }_{1,0},{\nu }_{2,0})\\ +{\displaystyle \sum _{j=1}^{\infty }}\left\{{\xi }_i\left({\displaystyle \sum _{k=0}^j}{\nu }_{1,k},{\displaystyle \sum _{k=0}^j}{\nu }_{2,k}\right)-{\xi }_i\left({\displaystyle \sum _{k=0}^{j-1}}{\nu }_{1,k},{\displaystyle \sum _{k=0}^{j-1}}{\nu }_{2,k}\right)\right\},\\ ={\displaystyle \sum _{j=0}^{\infty }}{G}_{i,j}.& (4)\end{array}$

where $G_{i,0}={\xi }_i({\nu }_{1,0},{\nu }_{2,0})and{G}_{i,j}={\xi }_i\left({\displaystyle \sum _{k=0}^j{\nu }_{1,k}},{\displaystyle \sum _{k=0}^j{\nu }_{2,k}}\right)-{\xi }_i\left({\displaystyle \sum _{k=0}^{j-1}{\nu }_{1,k}},{\displaystyle \sum _{k=0}^{j-1}{\nu }_{2,k}}\right),j\ge 1.i=1,2.$

Hence, equation (1) is equivalent to:

$\begin{array}{ll}{\displaystyle \sum _{j=0}^{\infty }}{\nu }_{i,j}=f_i+{\displaystyle \sum _{j=0}^{\infty }}{\varsigma }_i({\nu }_{1,j},{\nu }_{1,j})+{\displaystyle \sum _{j=0}^{\infty }}{G}_{i,j}.& (5)\end{array}$

Further, the recurrence relation is defined as follows:

$\begin{array}{l}{\nu }_{i,0}=f_i,\\ v_{i,1}={\varsigma }_i\left({\nu }_{1,0},{\nu }_{2,0}\right)+G_{i,0},\\ v_{i,2}={\varsigma }_i\left({\nu }_{1,1},{\nu }_{2,1}\right)+G_{i,1},\\ ..\dots \\ v_{i,m+1}={\varsigma }_i\left({\nu }_{1,m},{\nu }_{2,m}\right)+G_{i,m},m=1,2,..\dots & (8)\end{array}$

The kth-order approximation is given by:

$\begin{array}{l}{\nu }_i={\displaystyle \sum _{j=0}^{k-1}}{\nu }_{i,j}.\end{array}$

For convergence analysis, we refer to Daftardar-Gejji and Jafari [13] where explanatory example is solved.

Laplace Transform and Fractional Partial Differential Equations [4]

Consider the following equations:

$\begin{array}{ll}{D}_t^{\alpha }{v}_i(x,t)+\varsigma v_i(x,t)+\xi v_i(x,t)=0,& (7)\end{array}$

0 < α ≤ 1,

with ICs.

$\begin{array}{ll}{v}_i(x,0)=f_i(x).& (8)\end{array}$

where ς is the linear operator, ξ is the non-linear operator, and $D_t^{\alpha }{v}_i(x,t)$ is the Caputo fractional derivative of a function v_i(x, t), which is defined as:

$\begin{array}{ll}{D}_t^{\alpha }{v}_i(x,t)=\frac{1}{\Gamma (n-\alpha )}{\displaystyle \underset{0}{\overset{t}{\int }}}(\frac{{v_i}^n(x,\gamma )}{{(t-\gamma )}^{\alpha +1-n}})d\gamma ,& (9)\end{array}$

(n − 1 < α ≤ n, n ∈ N).

Using the property of Laplace transform for Caputo fractional derivatives is:

$\begin{array}{ll}L[D_t^{\alpha }{v}_i]=s^{\alpha }L[v_i(x,t)]-{\displaystyle \sum _{k=0}^{n-1}}{v_i}^k(x,0^{+})s^{\alpha -1-k}.& (10)\end{array}$

Taking the Laplace transform on both sides of equation (10) we get:

$\begin{array}{ll}L[D_t^{\alpha }{v}_i(x,t)]+L[\varsigma v_i(x,t)]+L[\xi v_i(x,t)]=0.& (11)\end{array}$

Using equation (10), we have:

$\begin{array}{ll}L[v_i(x,t)]=\frac{1}{s}{v}_i(x,0)-\frac{1}{s^{\alpha }}L[\varsigma v_i(x,t)]-\frac{1}{s^{\alpha }}L[\xi v_i(x,t)].& (12)\end{array}$

Taking the inverse Laplace transform on both sides of equation (12), we get:

$\begin{array}{l}{v}_i(x,t)=v_i(x,0)-L^{-1}[\frac{1}{s^{\alpha }}L[\varsigma v_i(x,t)]]\\ -L^{-1}[\frac{1}{s^{\alpha }}L[\xi v_i(x,t)]].& (13)\end{array}$

Now, we apply a new iterative technique that was derived in the New Iterative Method section.

Application of Laplace Transform With DJ Method to Fractional Whitham-Broer-Kaup Equations

Problem 3.1: Time Fractional WBK Equation

$\begin{array}{r}{D}_t^{\alpha }u+u{u}_x+v_x+b{u}_{xx}=0,\\ D_t^{\alpha }v+{(uv)}_x+a{u}_{xxx}-b{v}_{xx}=0.& (14)\end{array}$

Subject to ICs

$\begin{array}{r}u(x,0)=\lambda -2Bkcoth(k\xi ),\\ v(x,0)=-2B(B+b)k^{2}csc{h}^2(k\xi ),& (15)\end{array}$

where $\beta =\sqrt{a+b^2},\xi =x+c$and λ, c, k, are any constants.

For α = 1, the exact solution of the system is as follows:

$\begin{array}{r}u(x,t)=\lambda -2Bkcoth(k(\xi -\lambda t)),\\ v(x,t)=-2B(B+b)k^{2}csc{h}^2(k(\xi -\lambda t)).& (16)\end{array}$

Applying Laplace transform and inverse Laplace transform to equation (3.1), we have:

$\begin{array}{l}u(x,t)=u(x,0)\\ +L^{-1}[\frac{1}{S^{\alpha }}L[-\left(u(x,t)u_x(x,t)+v_x(x,t)+b{u}_{xx}(x,t)\right)]],\\ v(x,t)=v(x,0)+L^{-1}[\frac{1}{S^{\alpha }}L[-({(u(x,t)v(x,t))}_x\\ +a{u}_{xxx}(x,t)-b{v}_{xx}(x,t))]].& (17)\end{array}$

Now, using the basic idea of the DJ method discussed in the Fundamental Theory of Proposed Method section, we have:

$\begin{array}{r}{u}_0=\lambda -2Bkcoth(k\xi ),\\ v_0=-2B(B+b)k^{2}csc{h}^2(k\xi ),& (18)\end{array}$

$\begin{array}{ll}{u}_1=\frac{-2B{k}^2{t}^{\alpha }\lambda csc{h}^2(k(x+c))}{\Gamma (1+\alpha )},& (19)\end{array}$

$\begin{array}{l}{v}_1=\frac{1}{\Gamma (1+\alpha )}4B{k}^3{t}^{\alpha }\csc h^2(k(x+c))(-(b+B)\lambda \coth (k(x+c))\\ -(a+b^2-B^2)k(2+3\csc h^2(k(c+x)))),& (20)\end{array}$

$\begin{array}{l}{u}_2=\frac{1}{{(\Gamma (1+\alpha ))}^2\Gamma (1+2\alpha )\Gamma (1+3\alpha )}(2B{k}^3{t}^{2\alpha }\coth (k(x+c))\csc h^4\\ (k(x+c))(4B{k}^2{t}^{\alpha }{\lambda }^2{(\Gamma (1+2\alpha ))}^2+(-20(a+b^2-B^2)k^2+{\lambda }^2-\\ (4(a+b^2-B^2)k^2+{\lambda }^2)\cos h(2k(x+c))){(\Gamma (1+\alpha ))}^2\Gamma (1+3\alpha ))),& (21)\end{array}$

$\begin{array}{l}{v}_2=B{k}^4{t}^{2\alpha }\csc h^6(k(x+c))\\ [\frac{1}{\sqrt{\pi }\Gamma (1+\alpha )\Gamma (1+3\alpha )}{2}^{3+2\alpha }B{k}^2{t}^{\alpha }\lambda \csc h(k(x+c))\end{array}$

$\begin{array}{l}\Gamma (\frac{1}{2}+\alpha )(16(a+b^2-B^2)k\cosh (k(x+c))\\ +2(a+b^2-B^2)k\cosh (3k(x+c))\\ +(b+B)\lambda (2\mathrm{ sinh}(k(c+x))+\sinh (3k(x+c))))\\ -\frac{1}{\Gamma (1+2\alpha )}(12(11b-5B)(a+b^2-B^2)k^2\\ -3(b+B){\lambda }^2+2(4(13b-7B)(a+b^2-B^2)k^2\\ +(b+B){\lambda }^2)\cosh (2k(x+c))+(4(b-B)(a+b^2-B^2)k^2\\ +(b+B){\lambda }^2)\cosh (4k(x+c))\\ +4(a+b^2-B^2)k\lambda (10\sinh (2k(x+c))+\sinh (4k(x+c))))].& (22)\end{array}$

Three terms approximate the solution for equation (14):

$\begin{array}{r}u=u_0+u_1+u_2,\\ v=v_0+v_1+v_2.& (23)\end{array}$

We take k = 0.1, λ = 0.005, a = b = 1.5 and c = 10 in the above problem.

Problem 3.2: Time Fractional MB Equation

$\begin{array}{r}{D}_t^{\alpha }u+u{u}_x+v_x=0,\\ D_t^{\alpha }v+{(uv)}_x+u_{xxx}=0,& (24)\end{array}$

Subject to ICs

$\begin{array}{l}u(x,0)=\lambda -2kcoth(k\xi ),\\ v(x,0)=-2k^{2}csc{h}^2(k\xi ).& (25)\end{array}$

where ξ = x + c and k, λ, c are arbitrary constants.

For α = 1, the exact solution of the system is as follows:

$\begin{array}{r}u(x,t)=\lambda -2kcoth(k(\xi -\lambda t)),\\ v(x,t)=-2k^{2}csc{h}^2(k(\xi -\lambda t)).& (26)\end{array}$

According to the DJ method described in the Fundamental Theory of Proposed Method section, we have:

$\begin{array}{r}u(x,t)=u(x,0)+L^{-1}[\frac{1}{S^{\alpha }}L[-(u(x,t)u_x(x,t)+v_x(x,t))]],\\ v(x,t)=v(x,0)+L^{-1}[\frac{1}{S^{\alpha }}L[-({(u(x,t)v(x,t))}_x+u_{xxx}(x,t))]],& (27)\end{array}$

so that

$\begin{array}{r}{u}_0=\lambda -2kcoth(k(x+c)),\\ v_0=-2k^{2}csc{h}^2(k(x+c)),& (28)\end{array}$

$\begin{array}{ll}{u}_1=-\frac{2k^2{t}^{\alpha }\lambda csc{h}^2(k(x+c))}{\Gamma (1+\alpha )},& (29)\end{array}$

$\begin{array}{ll}{v}_1=-\frac{4k^3{t}^{\alpha }\lambda coth(k(x+c))csc{h}^2(k(x+c))}{\Gamma (1+\alpha )},& (30)\end{array}$

$\begin{array}{l}{u}_2=\frac{2k^3{t}^{2\alpha }{\lambda }^2\csc h^4(k(x+c))}{\Gamma (1+2\alpha )}\{\frac{4k^2{t}^{\alpha }\coth (k(x+c)){(\Gamma (1+2\alpha ))}^2}{{(\Gamma (1+\alpha ))}^2\Gamma (1+3\alpha )}\\ -\sinh (2k(x+c))\},& (31)\end{array}$

$\begin{array}{c}{v}_2=\frac{4k^4{t}^{2\alpha }{\lambda }^2\csc h^4(k(x+c))}{\Gamma (1+2\alpha )}\{-2-\cosh (2k(x+c))+\\ \frac{2k^2{t}^{\alpha }(3+2\cosh (2k(x+c)))\csc h^2(k(x+c)){(\Gamma (1+2\alpha ))}^2}{{(\Gamma (1+\alpha ))}^2\Gamma (1+3\alpha )}\}.& (32)\end{array}$

Three terms approximate the solution for equation (25):

$\begin{array}{r}u=u_0+u_1+u_2,\\ v=v_0+v_1+v_2.& (33)\end{array}$

Problem 3.3: Time Fractional ALW Equation

$\begin{array}{r}{D}_t^{\alpha }u+u{u}_x+\frac{1}{2}{u}_{xx}+v_x=0,\\ D_t^{\alpha }v+{(uv)}_x-\frac{1}{2}{v}_{xx}=0,& (34)\end{array}$

subject to Ics

$\begin{array}{r}u(x,0)=\lambda -kcoth(k\xi ),\\ v(x,0)=-k^{2}csc{h}^2(k\xi ).& (35)\end{array}$

where ξ = x + c and λ, c, k are arbitrary constants.

For α = 1, the exact solution of the system is as follows:

$\begin{array}{r}u(x,t)=\lambda -kcoth(k(\xi -\lambda t)),\\ v(x,t)=-k^{2}csc{h}^2(k(\xi -\lambda t)).& (36)\end{array}$

According to the DJ method described in the Fundamental Theory of Proposed Method section, we have:

$\begin{array}{l}u(x,t)=u(x,0)\\ +L^{-1}[\frac{1}{S^{\alpha }}L[-(u(x,t)u_x(x,t)+v_x(x,t)+\frac{1}{2}{u}_{xx}(x,t))]],\\ v(x,t)=v(x,0)+L^{-1}[\frac{1}{S^{\alpha }}L[-({(u(x,t)v(x,t))}_x-\frac{1}{2}{v}_{xx}(x,t))]].& (37)\end{array}$

So that

$\begin{array}{r}{u}_0=\lambda -kcoth(k(x+c)),\\ v_0=-k^{2}csc{h}^2(k(x+c)),& (38)\end{array}$

$\begin{array}{ll}{u}_1=-\frac{k^2{t}^{\alpha }\lambda csc{h}^2(k(x+c))}{\Gamma (1+\alpha )},& (39)\end{array}$

$\begin{array}{ll}{v}_1=-\frac{2k^3{t}^{\alpha }\lambda coth(k(x+c))csc{h}^2(k(x+c))}{\Gamma (1+\alpha )},& (40)\end{array}$

$\begin{array}{l}{u}_2=\frac{1}{\Gamma (1+2\alpha )}{k}^3{t}^{2\alpha }{\lambda }^{2}csc{h}^4(k(x+c))\\ \{\frac{2k^2{t}^{\alpha }coth(k(x+c)){(\Gamma (1+2\alpha ))}^2}{{(\Gamma (1+\alpha ))}^2\Gamma (1+3\alpha )}-sinh(2k(c+x))\},& (41)\end{array}$

$\begin{array}{l}{v}_2=\frac{2k^4{t}^{2\alpha }{\lambda }^2\csc h^4(k(x+c))}{\Gamma (1+2\alpha )}\{-2-\cosh (2k(x+c))\\ +\frac{1}{{(\Gamma (1+\alpha ))}^2\Gamma (1+3\alpha )}(k^2{t}^{\alpha }\\ (3+2\cosh (2k(x+c)))\csc h^2(k(x+c)){(\Gamma (1+2\alpha ))}^2)\}.& (42)\end{array}$

Three terms approximate the solution for equation (26):

$\begin{array}{r}u=u_0+u_1+u_2,\\ v=v_0+v_1+v_2.& (43)\end{array}$

Values of the parameters are taken to be same as problem 3.1.

Results and Discussion

The DJ method is experienced upon the fractional WBK, MB, and ALW equations. Mathematical 7 have been used for most computations.

Tables 1–3 show the estimation of absolute errors of the second-order DJ solution with ADM, VIM, and second-order OHAM solutions for u(x, t) of fractional WBK, MB, and ALW equations at α = 1, respectively. Tables 4–6 shows the estimation of absolute errors of second-order DJ solution with ADM, VIM, and second-order OHAM solutions for v(x, t) of fractional WBK, MB, and ALW equations at α = 1, respectively. The tabulated results show that the second-order approximate solutions by the DJ method are closer to exact solutions than those of ADM, VIM, and OHAM solutions.

TABLE 1

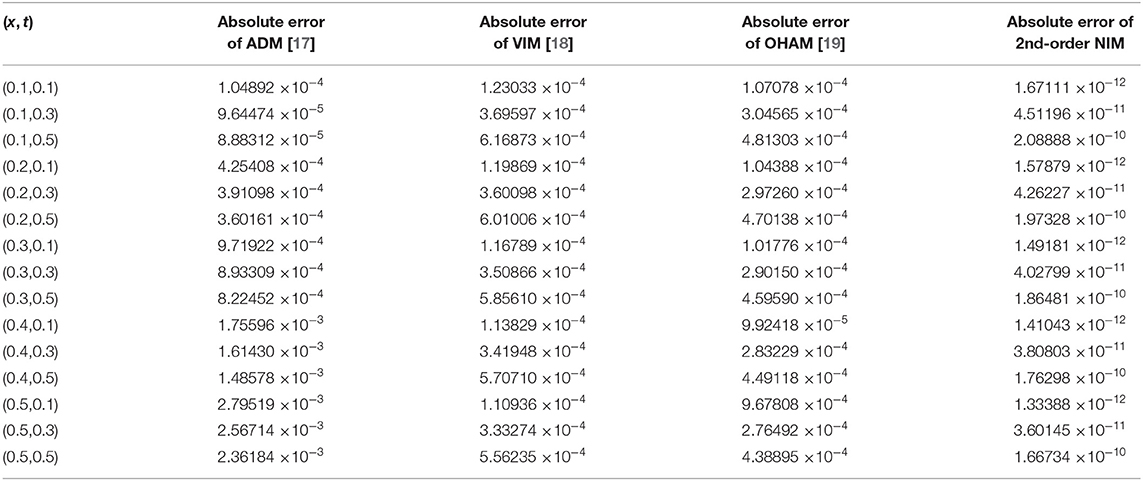
Table 1. Second-order DJ solution for u(x, t) in comparison with ADM, VIM, and OHAM solutions at α = 1 for WBK equation.

TABLE 2

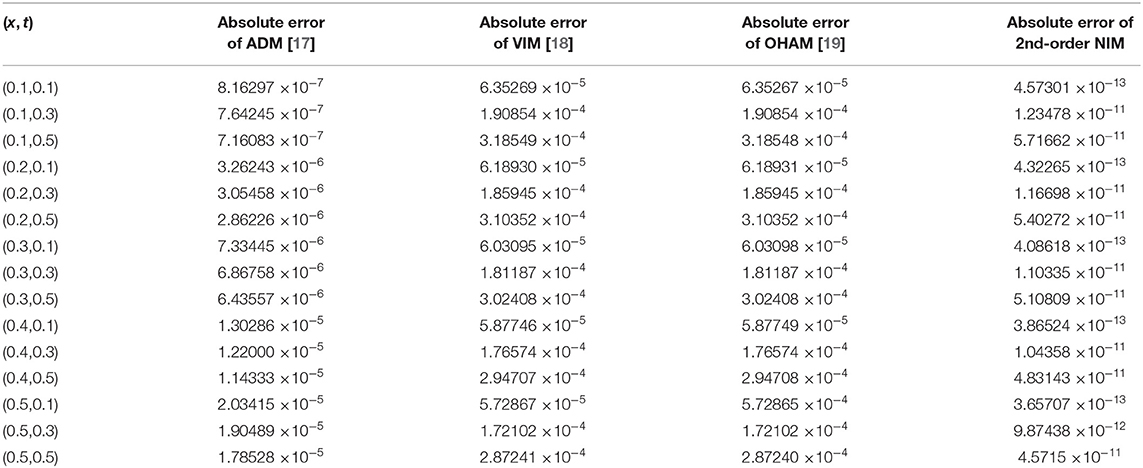
Table 2. Second-order DJ solution for u(x, t) in comparison with ADM, VIM, and OHAM solutions at α = 1 for MB equation.

TABLE 3

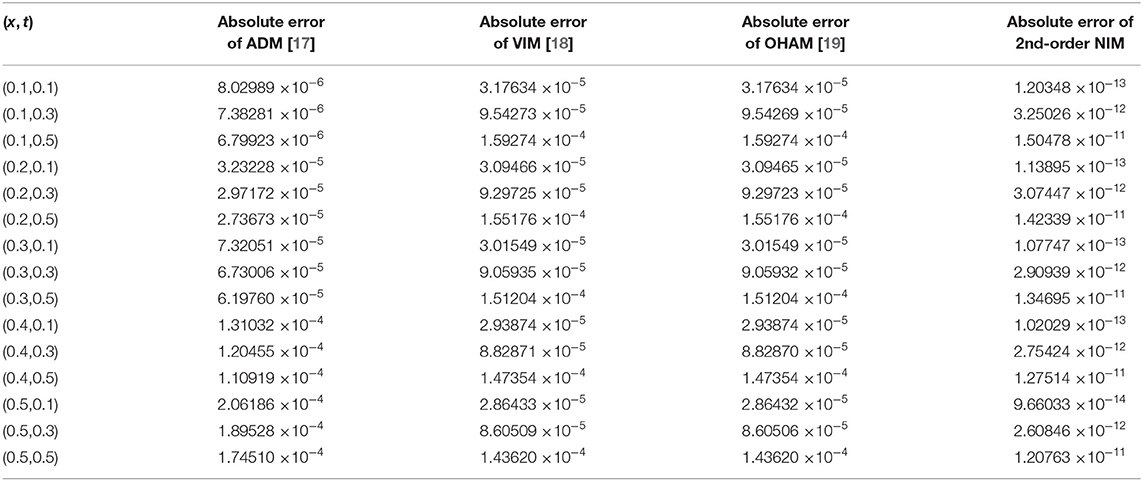
Table 3. Second-order DJ solution for u(x, t) in comparison with ADM, VIM, and OHAM solutions at α = 1 for ALW equation.

TABLE 4

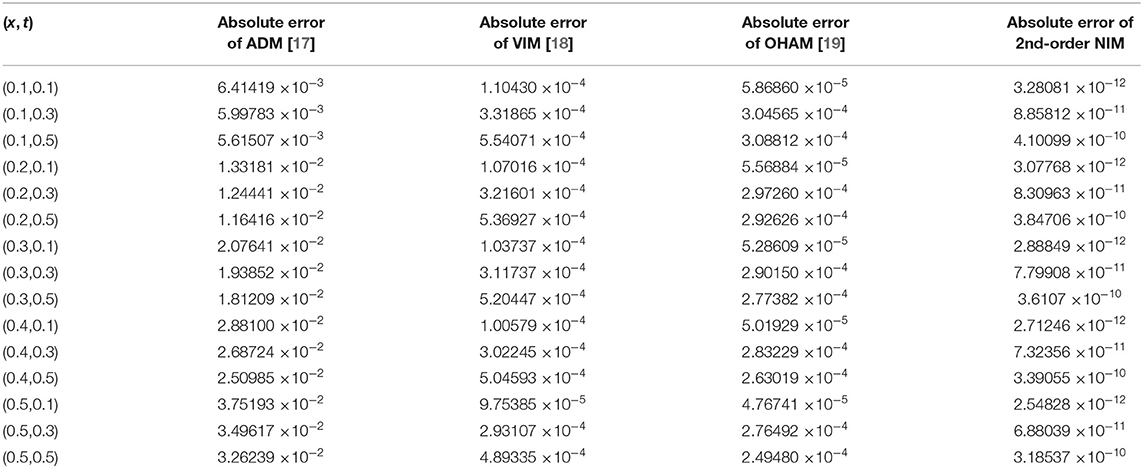
Table 4. Second-order DJ solution for v(x, t) in comparison with ADM, VIM, and OHAM solutions at α = 1 for WBK equation.

TABLE 5

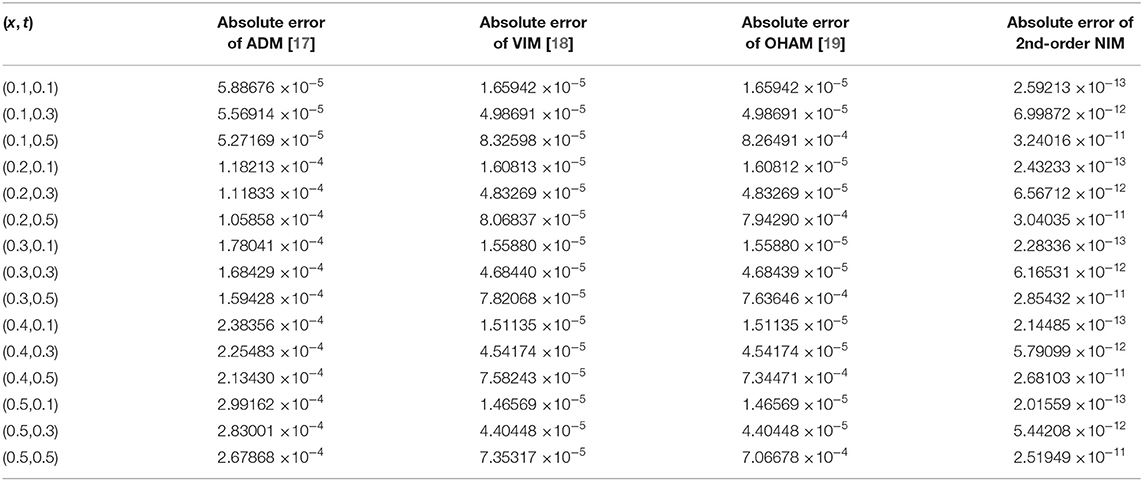
Table 5. Second-order DJ solution for v(x, t) in comparison with ADM, VIM, and OHAM solutions at α = 1 for MB equation.

TABLE 6

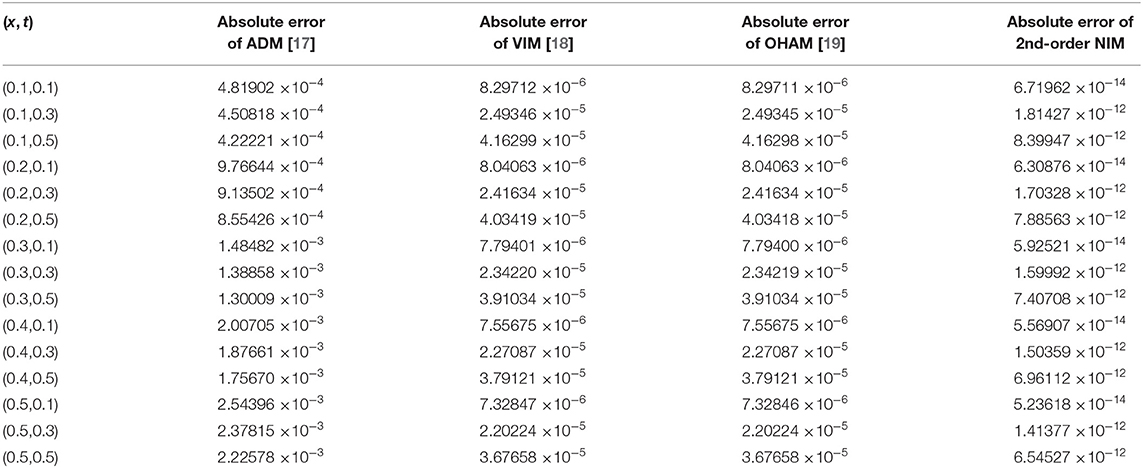
Table 6. Second-order DJ solution for v(x, t) in comparison with second-order ADM, VIM, and OHAM solutions at α = 1 for ALW equation.

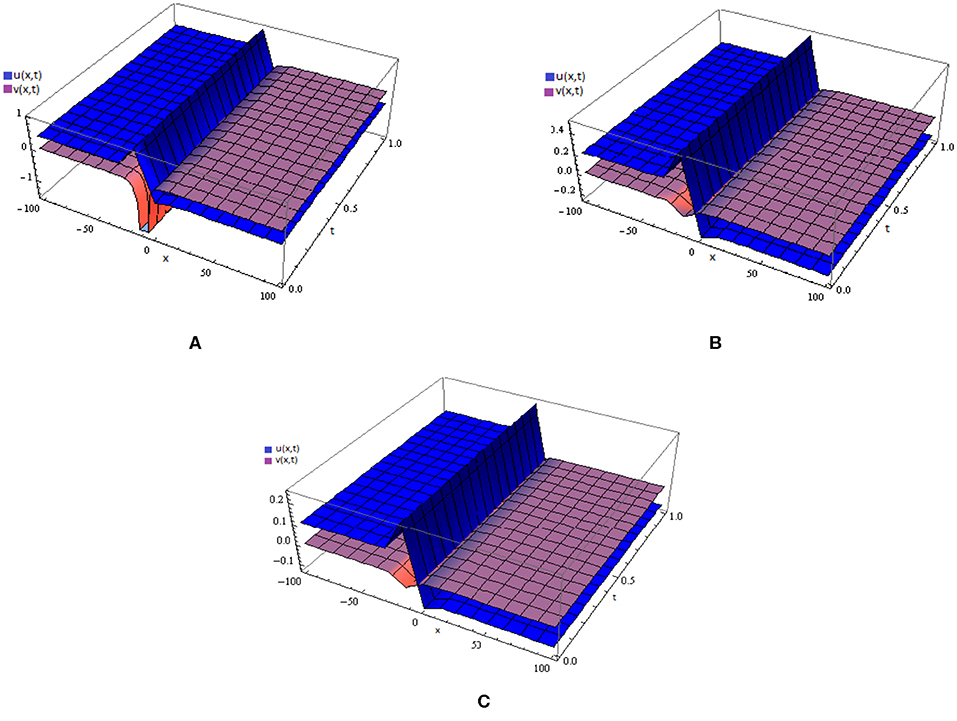
Figures 1A–C show the coupled surface of the second-order approximate solution by NIM for u(x, t) and v(x, t), part of WBK, MB, and ALW equations at α = 1, respectively. Figures 2, 3 show the 2D plots of the second-order approximate solution by NIM for u(x, t) and v(x, t) of WBK, MB, and ALW equations at x = 1 and different values of α, respectively. Figures 4A–C show the absolute error graph for the coupled WBK, MB, and ALW equation at x = 50.

FIGURE 1

Figure 1. (A) Coupled surface for WBK equation, (B) for MB equation, (C) for ALW equation at α = 1.

FIGURE 2

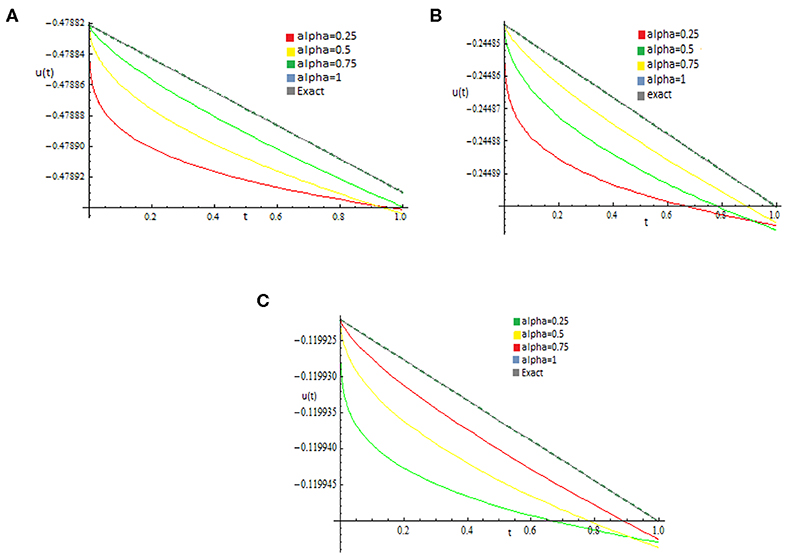
Figure 2. 2D curves for u(x, t) part of (A) WBK equation, (B) MB equation, (C) ALW equation at x = 1.

FIGURE 3

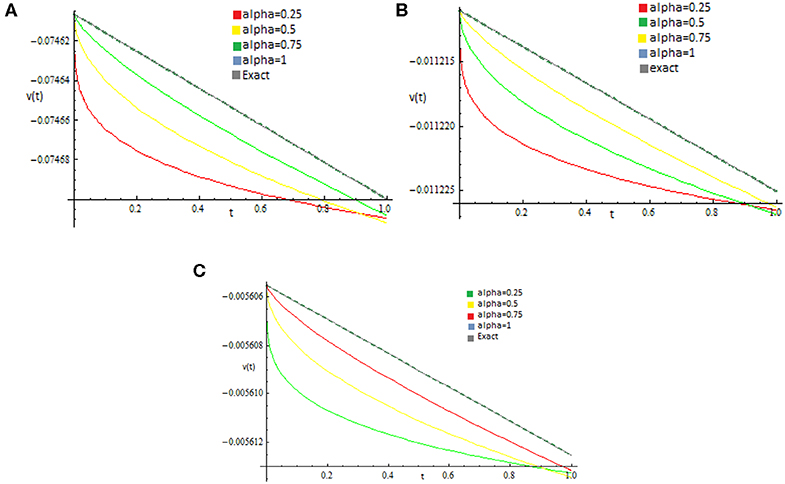
Figure 3. 2D curves for v(x, t) part of (A) WBK equation, (B) MB equation, (C) ALW equation at x = 1.

FIGURE 4

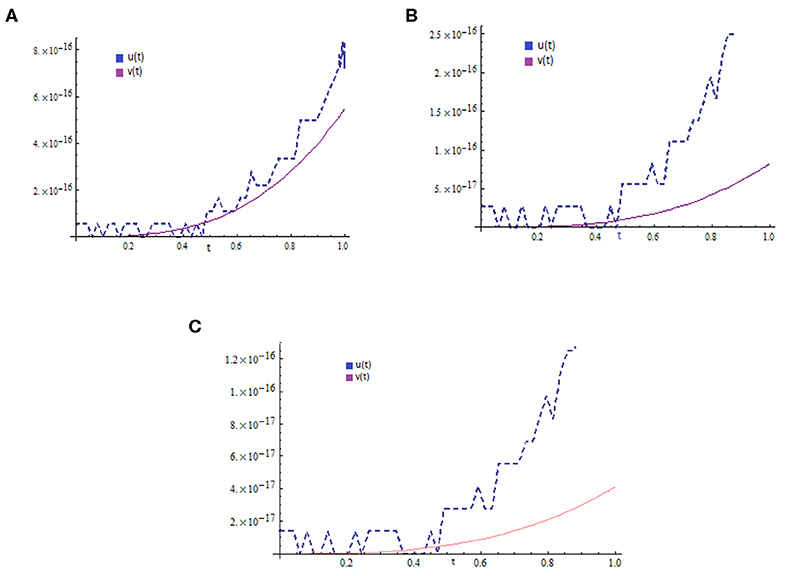
Figure 4. Absolute error curves for coupled (A) WBK equation, (B) MB equation, (C) ALW equation at x = 50.

It is clear from 2D figures that as the value of α increases to 1, the approximate solutions tend closer to the exact solution.

Conclusion

The DJ method converges rapidly to the exact solution at lower order of approximations for the WBK system. The results obtained by the proposed method are very encouraging in assessment with ADM, VIM, and OHAM. As a result, it would be more appealing for researchers to apply this method for solving systems of non-linear PDEs in different fields of science especially in fluid dynamics and physics. The accurateness of the technique can more be improved by taking higher-order estimation of the proposed method.

Data Availability Statement

All data and related metadata underlying the findings is reported in a submitted article.

Author Contributions

RN and PK developed the numerical method and led the manuscript preparation. ZS and SF contributed to the code development and to the article preparation. MS and WD contributed to the analysis and discussion of the results and help in revision. All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This project was supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.

References

1. Babeai A, Jafari H, Ahmadi M. A fractional order HIV/AIDS model based on the effect of screening of unaware infectives. Meth Appl Sci. (2019) 42:2334–43. doi: 10.1002/mma.5511

CrossRef Full Text | Google Scholar

2. Kadkhoda N, Jafari H. An analytical approach to obtain exact solutions of some space-time conformable fractional differential equations. Adv Differ Equ. (2019) 2019:428. doi: 10.1186/s13662-019-2349-0

CrossRef Full Text | Google Scholar

3. Javeed S, Baleanu D, Waheed A, Shaukat Khan M, Affan H. Analysis of homotopy perturbation method for solving fractional order differential equations. Mathematics. (2019) 7:40. doi: 10.3390/math7010040

CrossRef Full Text | Google Scholar

4. Singh PK, Vishal K, Som T. Solution of fractional Drinfeld-Sokolov-Wilson equation using homotopy perturbation transform method. Appl Math. (2015). 10:460-472.

Google Scholar

5. Demir A, Bayrak MA, Ozbilg E. A new approach for the approximate analytical solution of space-time fractional differential equations by the homotopy analysis method. Adv Math Phys. (2019) 2019:12. doi: 10.1155/2019/5602565

CrossRef Full Text | Google Scholar

6. Singh A, Das S, Ong SH, Jafari H. Numerical solution of nonlinear reaction-advection-diffusion equation, J Comput Nonlinear Dynamics. (2019) 14:041003. doi: 10.1115/1.4042687

CrossRef Full Text | Google Scholar

7. Az-Zo'bi E. A, exact analytic solutions for nonlinear diffusion equations via generalized residual power series method. Int. J. Math. Comput Sci. (2019) 4:69-78.

Google Scholar

8. Atangana AD. Baleanu. Nonlinear fractional jaulent-miodek and whitham-broer-kaup equations within sumudu transform. Abs Appl Anal. (2013). 2013:160681. doi: 10.1155/2013/160681

CrossRef Full Text | Google Scholar

9. Ali A, Shah K, Khan RA. Numerical treatment for solving wave solutions of fractionalwhitham-broer-kaupequations. Alexan Eng J. (2018) 57:1991–8. doi: 10.1016/j.aej.2017.04.012

CrossRef Full Text | Google Scholar

10. wang Y, Zhang YF, Jiang Z, Iqbal M. A fractional whitham-Broer-Kaup equation and its possible application to tsunami prevention. Ther Sci. (2017) 24:1847–55. doi: 10.2298/TSCI160510079W

CrossRef Full Text | Google Scholar

11. Guo S, Mei L, Li Y, Sun Y. The improved fractional sub equation method and its applications to the space-time fractional differential equations in fluid mechanics. Phys Lett A. (2012) 376:407–11. doi: 10.1016/j.physleta.2011.10.056

CrossRef Full Text | Google Scholar

12. Bhalekar S, Daftardar-Geji V. Solving a system of nonlinear functional equations using revised new iterative method. Int. J. Math. Comp Phys Elect Comp Eng. (2012) 6:8–21. doi: 10.1155/2012/975829

CrossRef Full Text | Google Scholar

13. Daftardar-Gejji V, Jafari H. An iterative method for solving nonlinear functional equations. J Math Anal Appl. (2006) 316:753–63. doi: 10.1016/j.jmaa.2005.05.009

CrossRef Full Text | Google Scholar

14. Khalouta A, Kadem A. Comparison of new iterative method and natural homotopy perturbation method for solving nonlinear time-fractional wave-like equations with variable coefficients. Nonlinear Dyn Syst Theory. (2019) 19:160–9.

Google Scholar

15. Khan MJ, Nawaz R, Farid S, Iqbal J. New iterative method for the solution of fractional damped burger and fractional Sharma-Tasso-Olver equations. Complexity. (2018) 2018:3249720. doi: 10.1155/2018/3249720

CrossRef Full Text | Google Scholar

16. Jena RM, Chakraverty S. A new iterative method based solution for fractional black-scholes option pricing equations (BSOPE). Appl Sci. (2019) 1:95. doi: 10.1007/s42452-018-0106-8

CrossRef Full Text | Google Scholar

17. El-Sayed SM, Kaya D. Exact and numerical traveling wave solutions of Whitham- Broer- Kaup equations. Appl Math Comput. (2005)167:1339–49. doi: 10.1016/j.amc.2004.08.012

CrossRef Full Text | Google Scholar

18. Rafei M, Daniali H. Application of the variational iteration method to the Whitham-Broer-Kaup equations. Comput Math Appl. (2007) 54:1079–85. doi: 10.1016/j.camwa.2006.12.054

CrossRef Full Text | Google Scholar

19. Sirajul H, Ishaq M. Solution of coupled Whitham-Broer-Kaup equations using optimal homotopy asymptotic method. Ocean Eng. (2014) 84:81–8. doi: 10.1016/j.oceaneng.2014.03.031

CrossRef Full Text | Google Scholar