Introducing the General Polytomous Diagnosis Modeling Framework

Although considerable developments have been added to the cognitive diagnosis modeling literature recently, most have been conducted for dichotomous responses only. This research proposes a general cognitive diagnosis model for polytomous responses—the general polytomous diagnosis model (GPDM), which combines the G-DINA modeling process for dichotomous responses with the item-splitting process for polytomous responses. The polytomous items are specified similar to dichotomous items in the Q-matrix, and the MML estimation is implemented using an EM algorithm. Under the general framework, different saturated forms, and some reduced forms, can be transformed linearly. Model assessment and adjustment under the dichotomous context can be extended to polytomous responses. This simulation study demonstrates the effectiveness of the model when comparing the two response types. The real-data example further illustrates how the proposed model can make a difference in practice.

Introduction

Cognitive diagnosis models (CDMs) have received increasing attention in educational and psychological measurement. CDMs are used to assess the strengths and weaknesses of test takers across a set of attributes. Diagnostic measurements based on CDMs can provide diagnostic and domain-specific information on finer grain size that can be used for different testing purposes. Recently, considerable developments had been added to the CDM literature. Among others, these included additive models like the additive CDM (A-CDM; de la Torre, 2011), the linear logistic model (LLM; Maris, 1999), and the reduced reparameterized unified model (R-RUM; Hartz, 2002; DiBello et al., 2007); highly constrained models like the deterministic inputs, noisy “and” gate (DINA; Junker and Sijtsma, 2001) model, and the deterministic inputs, noisy “or” gate (DINO; Templin and Henson, 2006) model; and saturated models like the log-linear CDM (LCDM; Henson et al., 2009) and the generalized DINA (G-DINA; de la Torre, 2011) model. Applied researchers are also equipped with models that can accommodate higher-order structure (de la Torre and Douglas, 2004), polytomous attributes (e.g., von Davier, 2008; Chen and de la Torre, 2013), multiple strategies (de la Torre and Douglas, 2008), partial credit (de la Torre, 2010), nominal responses (Templin et al., 2008; Chen and Zhou, 2017, March), and multiple-choice (MC) items (de la Torre, 2009). In terms of model assessment, various methods or procedures are provided for Q-matrix validation or more general model misfit (e.g., de la Torre, 2008; Chen et al., 2013; Chiu, 2013; de la Torre and Chiu, 2015; Chen, 2017). With these developments, one can find a growing number of CDM applications across different educational and psychological areas. Specifically, CDM-based measurement can be found in topics such as math (Tatsuoka, 1990), reading (Jang, 2009; Chen and Chen, 2015, 2016), psychological disorder (Templin and Henson, 2006), and situational judgment (García et al., 2014).

The significance of polytomous responses for diagnostic measurement has been realized for quite a while, with different conceptual models available (e.g., Rupp et al., 2010, p. 98). However, we can only identify three estimable CDM frameworks for polytomous responses up to date (von Davier, 2008; de la Torre, 2010; Ma and de la Torre, 2016). The partial-credit DINA model (de la Torre, 2010) is a direct extension of the highly constrained DINA model. In the general diagnostic model (GDM), von Davier (2008) accommodated polytomous responses based on the idea of the generalized partial credit model (GPCM; Muraki, 1992). The GDM framework for polytomous responses is a linearly additive model and no interaction term is involved (see Equation 2 in p. 290). The sequential CDM for polytomous responses (Ma and de la Torre, 2016) adopted the G-DINA model as the process function. But it required that the item categories were attained sequentially and associated with specific attributes explicitly, which might not be always applicable. Moreover, it is unclear how the monotonicity assumption that the probability of responding in higher category will increase monotonically for examinees with more required attributes can be satisfied. Although polytomous responses can be dichotomized, it is suboptimal, and can result in a dramatic loss of information. What is missing is a general, saturated framework for polytomous responses similar to the G-DINA model or LCDM for dichotomous responses, which can subsume a variety of reduced models.

Without a more general and comprehensive modeling framework for polytomous responses, the power of CDMs cannot be fully appreciated by applied researchers and practitioners across a wide range of areas. This research proposes a general cognitive diagnosis model for polytomous responses, the basic logic of which is to combine the G-DINA modeling process for dichotomous responses with the item-splitting process similar to the graded response modeling (Samejima, 1969). The G-DINA monotonicity constraint that examinees with more attributes will not have lower probability of success (Hong et al., 2016) is also extended to polytomous responses. The resulting model will be called the general polytomous diagnosis model (GPDM), which is saturated, and subsumes various saturated and reduced forms for polytomous and dichotomous responses. The marginal maximum likelihood (MML) estimation is adopted and implemented using an expectation-maximization (EM) algorithm. Although the GPDM will reduce to the G-DINA model for dichotomous responses, the varieties of reduced models within the GPDM exceed those under the G-DINA model, owing to the complexity of polytomous responses. Model assessment and adjustment under the dichotomous context will be also extended to polytomous responses.

Theoretical Framework

Model Formulation

For a diagnostic test with J items and K dichotomous attributes, there will be L = 2^K attribute patterns and a J × K Q-matrix. Let ${\alpha }_l^{}={({\alpha }_{l1},\cdots ,{\alpha }_{lK})}^T$ denote the attribute vector where l = 1, …, L, and q_jk is the element in row j and column k of the Q-matrix. Denote the polytomous responses for item j as X_j = c with C_j response categories, where c = 0, …, C_j – 1. For polytomous responses, one can specify q_jk as 1 if mastery of attribute k is required to respond c or above on item j, and as 0 otherwise for any c > 0. If one sets c > 1 (e.g., c = 2) however, it will result in a loss of information since any response below c will not be modeled (e.g., 1 will be treated as 0 when c = 2). Note that if one sets c = C_j – 1, the polytomous responses reduce to dichotomous responses. For maximal information, this research proposes to specify q_jk as 1 if mastery of attribute k is required to respond 1 or above to item j, and as 0 otherwise. Stated differently, instead of specifying each item category, one only needs to specify the polytomous items similar to dichotomous items in the Q-matrix. The modeling process will take care of the difference across item categories. Accordingly, the Q-matrix is subjected to same criteria of completeness or identifiability for dichotomous responses (e.g., Köhn and Chiu, 2016; Xu and Zhang, 2016).

For item j, irrelevant attributes can be omitted and the required attributes is represented by the reduced attribute vector ${\eta }_{jh}={({\eta }_{h1},\cdots {\eta }_{hg},\cdots ,{\eta }_{h{G}_j})}^T$, where $h=1,\dots ,H_j=2^{G_j}$ and $G_j={\sum }_{k=1}^K{q}_{jk}$. Similar to the G-DINA model (de la Torre, 2011), the attribute vector α_l is simplified as the reduced attribute vector η_jh, the elements of which correspond to the required attributes in Item j. It means that the L attribute patterns or latent classes of the whole test are simplified to H_j latent groups in item j. The simplification proceeds with the help of Item j's q-vector q_j. Note that attributes in the reduced vector should follow the same order as the required attributes in α_l. For a test with four attributes for example, ${\alpha }_l^{}={({\alpha }_{l1},{\alpha }_{l2},{\alpha }_{l3},{\alpha }_{l4})}^T$ and l = 1, …, L = 16. If only the first and third attributes are required in Item j, the q-vector is ${\text{q}}_j={(1,0,1,0)}^{}$. Accordingly, G_j = 2 and the reduced vector is ${\eta }_{jh}={({\eta }_{h1},{\eta }_{h2})}^T={({\alpha }_{l1},{\alpha }_{l3})}^T$, with h = 1, …, H_j = 4. Working with η_jh instead of α_l on Item j, one only needs to handle four, instead of 16, latent groups.

For latent variable modeling with polytomous responses, it is convenient to split the polytomous item with C_j response categories into C_j dichotomous sub-items, each of which then can be formulated using models for dichotomous responses. The GPDM splits the item indirectly based on the difference of cumulative probability between response categories. The probability of examinees responding c, conditional on reduced attribute vector η_jh, is P(X_j = c|η_jh) ≡ P_c(η_jh), with ${\displaystyle {\sum }_{c=0}^{C_j-1}{P}_c({\eta }_{jh})}=1$. The cumulative probability of response in Category c or above can be denoted as $P(X_j\ge c|{\eta }_{jh})\equiv P_c^{*}({\eta }_{jh})$. Under the graded response approach (Samejima, 1969), the relationship between the conditional and cumulative probabilities is:

$\begin{array}{rc}{P}_c^{*}({\eta }_{jh})-P_{c+1}^{*}({\eta }_{jh})=P_c({\eta }_{jh})& (1)\end{array}$

with $P_0^{*}({\eta }_{jh})=1$ and $P_{C_j}^{*}({\eta }_{jh})=0$. For item j, the number of independent probabilities in $P_c^{*}({\eta }_{jh})$ and P_c(η_jh) is the same and equals (C_j − 1)H_j. It is more straightforward to formulate the model directly with the conditional probabilities P_c(η_jh) rather than the cumulative probabilities $P_c^{*}({\eta }_{jh})$.

The monotonicity assumption under the G-DINA model for dichotomous responses (de la Torre, 2011) can be extended to polytomous response. Specifically, the relationship between two attribute vectors η_jh and η${}_{j{h}^{\prime }}$ can be defined as η_jh ≥ η${}_{j{h}^{\prime }}$ if and only if η_hg ≥ ${\eta }_{h^{\prime }g}$ for g = 1,…, G_j. Equality between the two vectors (i.e., η_jh = η${}_{j{h}^{\prime }}$) holds if and only if η_hg = ${\eta }_{h^{\prime }g}$ for g = 1,…, G_j. If η_jh > η${}_{j{h}^{\prime }}$, it means that attribute vector η_jh has more required attributes compared to η${}_{j{h}^{\prime }}$. In its most general formulation, the GPDM allows $P_c^{*}({\eta }_{jh})<P_c^{*}({\eta }_{j{h}^{\prime }})$ for η_jh > η${}_{j{h}^{\prime }}$. In many CDM applications however, it would be reasonable to impose the monotonicity assumption that $P_c^{*}({\eta }_{jh})\ge P_c^{*}({\eta }_{j{h}^{\prime }})$ whenever η_jh > η${}_{j{h}^{\prime }}$. Namely, the cumulative probability of responding in higher category will increase monotonically for examinees with more required attributes. Note that polytomous items with decreasing monotonicity (i.e., negative items) can be addressed by reversing the items, in case needed.

Using different linking functions, $P_c^{}({\eta }_{jh})$ can be linearly transformed into item effects in different saturated forms, as

$\begin{array}{l}F\left[P_c^{}({\eta }_{jh})\right]={\beta }_{jc0}+{\displaystyle \sum _{g=1}^{G_j}}{\beta }_{jcg}{\eta }_{hg}+{\displaystyle \sum _{g^{\prime }>g}^{G_j}}{\displaystyle \sum _{g=1}^{G_j-1}}{\beta }_{jcg{g}^{\prime }}{\eta }_{hg}{\eta }_{h{g}^{\prime }}\dots \\ +{\beta }_{jc12\dots G_j}{\displaystyle \prod _{g=1}^{G_j}}{\eta }_{hg},& (2)\end{array}$

where F(·) is a specific linking function and β_jc0, β_jcg, and ${\beta }_{jcg{g}^{\prime }}$ are the baseline, main, and interaction effects for Category c, respectively. Some widely used linking functions include the identity, logit, and log links. The conversion from P_c(η_jh) to different item effects β_jc. can be facilitated with a design matrix as discussed later. Note that model-data fit for different linking functions in saturated forms is theoretically identical since no estimation is involved. For dichotomous responses, the formulation is equivalent to the G-DINA model with the identity link or LCDM with the logit link functions.

Model Estimation

The above GPDM, in the saturated form with the identity linking function, can be estimated with the MML method and implemented using an EM algorithm. A large number of structural parameters can be involved as the number of attributes increases. Although it is possible to simplify the joint distribution of the attributes with specific constraints on the structural relationships (e.g., higher-order or hierarchical structures) in future studies, this research only considers the general or unconstrained structure. In general, there are (L-1) independent structural parameters p(α_l), which is the prior probability of the attribute vector α_l with ${\sum }_{l=1}^{L}p({\alpha }_l)=1$. Denote X_ijc = 1 if X_ij = c and zero otherwise. The conditional likelihood of the response data X_i for examinee i given α_l is

$\begin{array}{rc}L({\text{X}}_i|{\alpha }_l)={\prod }_{j=1}^J{\prod }_{c=0}^{C_j-1}{P}_c{({\eta }_{jh})}^{X_{ijc}}& (3)\end{array}$

where the attribute vector α_l is reduced to the reduced attribute vector η_jh for item j. The marginalized likelihood of the data is

$\begin{array}{rc}L(\text{X})={\prod }_{i=1}^{N}L({\text{X}}_i)={\prod }_{i=1}^N{\sum }_{l=1}^{L}L({\text{X}}_i|{\alpha }_l)p({\alpha }_l),& (4)\end{array}$

where N is the sample size. The MML estimation of the conditional probabilities ${\widehat{P}}_c({\eta }_{jh})$ can be implemented with an EM algorithm. The standard error (SE) of the estimate, $SE[{\widehat{P}}_c({\eta }_{jh})]$, can be approximated with the information matrix given by the second derivative of the log-marginalized likelihood with respect to P_c(η_jh) and $P_{c^{\prime }}({\eta }_{j{h}^{\prime }})$. Details of an algorithm for the estimates ${\widehat{P}}_c({\eta }_{jh})$ and corresponding SEs can be found in the Appendix in Supplementary Material.

During each iteration of the estimation, the monotonicity assumption can be imposed top-down as a constraint with the help of (1). For an item with four categories for instance, one can first impose the constraint on the top category with $P_3^{*}({\eta }_{jh})=P_3({\eta }_{jh})$, and then on the second top category with $P_2^{*}({\eta }_{jh})=P_2({\eta }_{jh})+P_3^{*}({\eta }_{jh})$, till the second lowest category with $P_1^{*}({\eta }_{jh})=P_1({\eta }_{jh})+P_2^{*}({\eta }_{jh})$. For each category, one can choose between the upward or downward approaches to implement the constraint, although the upward one would be generally preferred as in the case for dichotomous response (Hong et al., 2016). Alternatively, one can choose to check the monotonicity assumption post hoc (i.e., after the estimation), which could help to inform item development.

Different Saturated and Reduced Forms

The GPDM is a saturated model, with equivalent saturated forms, and subsumes a variety of reduced CDMs for polytomous and dichotomous responses. For different saturated forms and some reduced forms, the estimates ${\widehat{P}}_c({\eta }_{jh})$ can be linearly transformed to item parameters (i.e., item effects or β_jc.) without requiring additional estimation. Corresponding linking functions and design matrices somewhat similar to those in the G-DINA model (de la Torre, 2011) can be used. The design matrix for item j, D_j, is a H_j × V matrix, where V is the number of item parameters of the targeted form. For other reduced forms however, the item parameters might involve a second step of estimation from ${\widehat{P}}_c({\eta }_{jh})$, which is beyond the scope of this research.

For saturated forms, the design matrix is a square matrix with element

$d_{h{h}^{\prime }}=\{\begin{array}{c}1\\ 0\end{array}\begin{array}{c}{\eta }_{jh}{\eta }_{j{h}^{\prime }}^T=G_j\\ otherwise\end{array},(5)$

where h and $h^{\prime }=1,\dots ,H_j$. The item parameters can be obtained by finding the least-squares estimate

$\begin{array}{rc}{\widehat{\beta }}_{jc}={(D_j^T{\text{D}}_j)}^{-1}{\text{D}}_j^{T}F({\widehat{\text{P}}}_{jc}),& (6)\end{array}$

where F(.) is the linking function (e.g., identity, logit, or log) and $P_{jc}={\left\{P_c({\eta }_{jh})\right\}}_{jc}$ includes all independent P_c(η_jh) for item j. The standard errors can be approximated via the multivariate delta method (Lehmann and Casella, 1998). Denote $f(·)\equiv {({\text{D}}_j^T{\text{D}}_j)}^{-1}{\text{D}}_j^{T}F(·)$ and ∇f(·) as the gradient of f (.). We have

$\begin{array}{rc}SE{({\widehat{\beta }}_{jc})}^2=Var\left[f({\widehat{\text{P}}}_{jc})\right]\approx \nabla f{({\widehat{\text{P}}}_{jc})}^{T}Var({\widehat{\text{P}}}_{jc})\nabla f({\widehat{\text{P}}}_{jc}),& (7)\end{array}$

where $Var({\widehat{\text{P}}}_{jc})$ is the negative of the inverse of the information matrix for ${\widehat{\text{P}}}_{jc}$.

By constraining the item parameters, one can get different reduced CDMs for polytomous responses. The DINA model for polytomous responses (PDINA) can be expressed as

$\begin{array}{rc}{P}_c^{}({\eta }_{jh})={\beta }_{jc0}+{\beta }_{jc12\dots G_j}{\displaystyle \prod _{g=1}^{G_j}}{\eta }_{hg},& (8)\end{array}$

with 2(C_j – 1) parameters per item. The conjunctive attribute relationship in the DINA model is extended to every above-zero category in the PDINA model. Consistent with terminology in previous literature, we can set g_jc = β_jc0 and s_jc = (1 − β_jc0 − β_jc12…Gj) as the guessing and slip parameter for Category c, respectively. Similarly, one can obtain the DINO model for polytomous responses (PDINO) by adopting the identity link with

$\begin{array}{rc}{P}_c^{}({\eta }_{jh})={\beta }_{jc0}+{\beta }_{jcg}{\eta }_{hg},& (9)\end{array}$

where

$\begin{array}{rc}{\beta }_{jcg}={\beta }_{jc{g}^{\prime }{g}^{″}}=\dots ={(-1)}^{G_j+1}{\beta }_{jc12\dots G_j},& (10)\end{array}$

for g = 1, …, G_j, $g^{\prime }=1,\dots ,G_j-1$, and $g^{″}>g^{\prime },\dots ,G_j$. PDINO also has 2(C_j – 1) parameters per item, and the compensatory attribute relationship in the DINO model is extended to every above-zero categories in the PDINO model. For this model, g_jc = β_jc0 and s_jc = (1 − β_jc0 − β_jcg) is the guessing and slip parameter respectively, for Category c. The item parameters of both the PDINA and PDINO models can be linearly transformed from the ${\widehat{\text{P}}}_{jc}$ using the design matrices, which are

$\begin{array}{rc}{\text{D}}_{j[H_j\times 2]}=\left(\begin{array}{cc}1& 0\\ 1& 0\\ ⋮& ⋮\\ 1& 0\\ 1& 1\\ \end{array}\right)& (11)\end{array}$

and

$\begin{array}{rc}{\text{D}}_{j[H_j\times 2]}=\left(\begin{array}{cc}1& 0\\ 1& 1\\ ⋮& ⋮\\ 1& 1\\ 1& 1\\ \end{array}\right)& (12)\end{array}$

for the PDINA and PDINO models, respectively. Moreover, to account for the relative size of the latent class, the item parameters of the above models should be weighted by the class size, as:

$\begin{array}{rc}{\widehat{\beta }}_{jc}={({\text{D}}_j^T{\text{W}}_j{\text{D}}_j)}^{-1}{\text{D}}_j^T{\text{W}}_j{\widehat{\text{P}}}_{jc}& (13)\end{array}$

where W_j = diag{N_jh} is a diagonal matrix, with $N_{jh}={\sum }_{i=1}^{N}p({\eta }_{jh}|{\text{X}}_i)$ as the expected number of examinees in latent group h of item j (i.e., with the reduced attribute vector η_jh). The standard errors of these estimates can also be computed as given in (7), except that $f({\widehat{\text{P}}}_{jc})$ is defined as ${({\text{D}}_j^T{\text{W}}_j{\text{D}}_j)}^{-1}{\text{D}}_j^T{\text{W}}_j{\widehat{\text{P}}}_{jc}$. Similar to the cases for dichotomous responses, a linear transformation of the saturated models to the reduced models is equivalent to a direct estimation of the reduced models using the same MML method (de la Torre and Chen, 2011).

However, not all reduced forms can be obtained through linear transformation. By dropping all interaction terms in (2), one can obtain different additive forms of CDMs for polytomous responses, as

$\begin{array}{rc}F\left[P_c^{}({\eta }_{jh})\right]={\beta }_{jc0}+{\displaystyle \sum _{g=1}^{G_j}}{\beta }_{jcg}{\eta }_{hg}& (14)\end{array}$

The formulation with the identity, logit, and log linking function corresponds to the A-CDM for polytomous response (PA-CDM), LLM for polytomous responses (PLLM), and R-RUM for polytomous responses (PR-RUM), respectively. The additive forms have a common feature that there are (C_j − 1)(G_j + 1) parameters or effects per item. Although the additive forms are subsumed under the GPDM, linear relationship between the (C_j − 1)(G_j + 1) item parameters and (C_j − 1)H_j ${\widehat{P}}_c({\eta }_{jh})$ estimates cannot be established, except for the case of a single attribute. Additional estimation analyses are required to obtain the item parameters of these reduced forms, which is not covered in this research but could be a topic for future studies.

Model Assessment and Adjustment

Model assessment and adjustment for dichotomous responses can be extended to polytomous responses. This research builds on the simulation- and residual-based method (Chen et al., 2013) and applies the correlation of item pairs for such purpose. Specifically, after obtaining the estimates P_c(η_jh) and p(α_l|X), one can simulate a large number of item responses by sampling from the multinomial distribution of the conditional probabilities and joint distribution of the attributes. Let X_j and ${\tilde{X}}_j$ denote the observed and predicted response vector for item j, respectively. The residual between the observed and predicted Fisher-transformation of correlation of item pairs (referred to as r) is

$\begin{array}{rc}{r}_{j{j}^{\prime }}=|Z[\rho ({\text{X}}_j,{\text{X}}_{j^{\prime }})]-Z[\rho ({\tilde{\text{X}}}_j,{\tilde{\text{X}}}_{j^{\prime }})]|,& (15)\end{array}$

where Z[ρ(·)] is the Fisher transformation of Pearson's correlation. The approximate SE can be computed as:

$\begin{array}{rc}SE(r_{j{j}^{\prime }})={\left[N-3\right]}^{1/2}.& (16)\end{array}$

With the SEs, the z-score of r can be computed. The expected response patterns can be simulated stably with a large sample size, although randomness is inevitable due to simulation. For an assessment with J items, (J – 1) and J(J – 1)/2 item pairs of z-scores need to be evaluated at the item and test levels, respectively.

One can examine the significance of the maximum z-score for model misfit at the test level, with the Bonferroni correction to control for the Type I errors (Chen et al., 2013). In case of misfit, we can use the root mean square (RMS) of the z-scores at the item level to identify possibly misspecified items, as

$\begin{array}{rc}s{r}_j={\left[{\sum }_{j^{\prime }=1}^J{(r_{j{j}^{\prime }}/SE(r_{j{j}^{\prime }}))}^2/(J-1)\right]}^{1/2}& (17)\end{array}$

The item with the maximum value sr_j (called the hit item) is most likely misspecified and should be considered for adjustment. The test-level RMS of the z-scores is

$\begin{array}{rc}sr={\left[2{\sum }_{j=1}^J{\sum }_{j^{\prime }=1}^{j-1}{(r_{j{j}^{\prime }}/SE(r_{j{j}^{\prime }}))}^2/J(J-1)\right]}^{1/2}& (18)\end{array}$

sr should be less sensitive to simulation randomness due to the accumulation of all residuals z-scores, and its reduction can aid in item adjustment. Findings for dichotomous responses (Chen, 2017) can be applied to polytomous responses. Misspecified items can be evaluated as the hit item and adjusted sequentially when Q-matrix misspecification occurs at the item level. Adjustments can proceed based on the maximum reduction of the sr statistics. Attribute-level misspecification is of concern when adjustment to individual items tends to be useless.

Simulation Study

Design

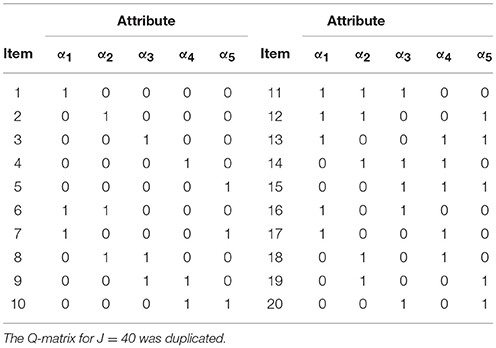
A simulation study was conducted to investigate if the GPDM can perform as expected. The true CDM was the PA-CDM with the identity link, and C_j = C = 3 for all items. The cumulative probabilities of the highest category, $P_2^{*}(0)$ and $P_2^{*}(1)$, were randomly generated from Unif (0.0, 0.3) and Unif (0.7, 1.0), respectively, with those of the middle category [i.e., $P_1^{*}(0)$ and $P_1^{*}(1)$] fixed as half of the highest category. It means that the conditional probabilities of both categories were equally contributed [i.e., P₁(0) = P₂(0) and P₁(1) = P₂(1)]. All main effects (i.e.,β_jk) were set to be equal so that each required attribute contributed equally to P_c(η_jh). The number of attributes K was fixed to five and the Q-matrix consisted of one- to three-attribute items, with each attribute specified the same number of times (Table 1). The number of items was set as J = 20 and 40, and two sample sizes were considered as N = 500 and 1,000. The Q-matrix for J = 40 is just twice the Q-matrix for J = 20.

TABLE 1

Table 1. Q-matrix for J = 20.

The multivariate normal threshold method (Chiu et al., 2009) was used to simulate the joint distribution of the attributes. One can assume a multivariate normal distribution, MVN(0, Σ), of K continuous latent variables underlying the K discrete attributes, with all variances and covariance in Σ equal to 1.0 and R, respectively. R is the correlations of the latent variables and was set as 0.5. In addition to the GPDM, the G-DINA model was also fitted to allow for comparisons. For the G-DINA model, the polytomous responses were converted to dichotomous by replacing responses in the highest category with 1 and those in other categories with 0. Each simulation cell was replicated 500 times, and the estimation code was written in Ox (Doornik, 2003)¹.

Results

Table 2 gives the mean estimates and related standard deviation (SD) of the classification accuracy for individual attributes [CA(α_k)] and for the attribute vector [CA(α_l)]. For both individual attributes and the attribute vector, the accuracy improved with the larger sample size or number of items. The number of items was more influential, especially on the attribute vector. Comparing the two models, the GPDM always produced more accurate classifications than the G-DINA model did, and the improvement was more dramatic for the attribute vector (about double or more) than individual attributes. The findings simply reflected the loss of diagnostic information by treating the polytomous responses as dichotomous under the settings used in this study. The classifications were also more stable (i.e., smaller SD) with either larger sample size or larger number of items for the GPDM, with the latter being more influential. For the G-DINA model, the classifications of the attribute vector were found to be more stable with a smaller number of items, or compared with those for the GPDM. Taking into account the CA(α_l) values however, the stability suggested that the G-DINA-based accuracy was consistently low under the situation.

TABLE 2

Table 2. Classification accuracy and related SD.

Although one cannot investigate the recovery of all item parameters as the true and fitted models were different, some item estimates can be evaluated. Specifically, the true and estimate P_c(0) and P_c(1) should be approximately identical with the GPDM. Table 3 gives the mean bias and root mean square error (RMSE) of the estimates of the conditional probabilities. As shown, both statistics improved with the larger sample size or number of items, with the former being slightly more influential. The item parameters were recovered equally well across the two response categories, reflecting the design of equal contribution of both categories.

TABLE 3

Table 3. Recovery of item estimates with the GPDM.

Real-Data Illustration

In this section real data were used to illustrate the application of the GPDM in practice and how different results one might get whether polytomous items were dichotomized or not. The PISA 2000 reading assessment (OECD, 1999, 2006a) with the released items (OECD, 2006b) was used, which contained both polytomous and dichotomous items. The data were retrofitted by some researchers with a new set of attributes (Chen and Chen, 2015), but only part of the released items were dichotomously fitted with the G-DINA model. With the same set of attributes and the help of same content experts, a subset of the released items was used to construct a Q-matrix (Table 4) for illustration purpose. The final data set consisted of responses of 1,039 English examinees to 20 items in specific test booklet, five out of which were polytomous. Both the GPDM and G-DINA model were fitted. For the G-DINA model, the polytomous items were again dichotomized by setting the highest level to 1 and all other levels to 0.

TABLE 4

Table 4. Items and Q-matrix for the PISA data.

Table 5 presents the results of model fitting and attribute estimation. For both models, the maximum z-score of r were well below the critical value at α = 0.1 significance level, suggesting that no misfit could be found for either model. However, there was slight to moderate difference in classifications across attributes between the two models, as shown by the attribute prevalence and classification consistency based on Cohen's kappa (to adjust for chance of consistency). The difference was most salient for Attribute 4, suggesting that the loss of information was most severe for this attribute if polytomous responses were dichotomized. As a result, only 68% of examinees were identically classified (i.e., same attribute vector) across the two models.

TABLE 5

Table 5. Fitting and attribute estimation for the PISA data.

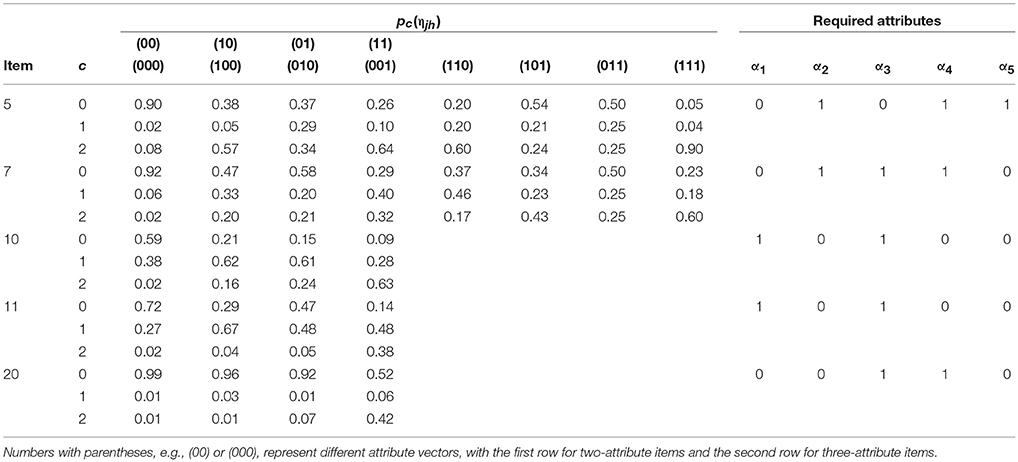
Table 6 presents the estimates of the polytomous items using the GPDM. Except for the last item, number 20, at least some of the conditional probabilities for the middle response category [i.e.,P₁(η_jh)] were not trivial. Among these polytomous items, examinees were most likely to get partial credit for Item 10 and 11. For both items, the conditional probabilities P₁(10) or P₁(01) > P₁(11) or P₁(00), whereas the cumulative probabilities $P_1^{*}(11)>P_1^{*}$(10) or $P_1^{*}(01)$. In reflection, this implied that the middle category (i.e., partial credit) was specifically oriented toward examinees mastering some but not all required attributes, which can be regarded as a useful way to design the item category. For Item 5 and 7, there was little chance to get partial credit for some reduced attribute patterns (e.g., 000). The small values of all P₁(η_jh) for Item 20 suggested that the middle category was unnecessary. Finally, the monotonicity assumption was not imposed, and one can find that there were some mild violations in Item 5 [e.g., $P_2^{*}(001)>P_2^{*}(101)$ or $P_2^{*}(011)$] and Item 7 [e.g., $P_1^{*}(001)>P_1^{*}(110)$ or $P_1^{*}(011)$], which might be useful information to adjust the items.

TABLE 6

Table 6. Estimates of conditional probabilities for polytomous items.

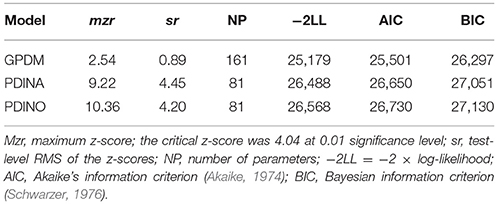
Table 7 compares the model-data fits between the saturated GPDM and the reduced PDINA or PDINO models. Both reduced models were worse than the saturated model based on any of the relative fit indices. Furthermore, both the PDINA and PDINO models were rejected at α = 0.01 significance level based on the maximum z-score, which suggests that highly constrained relationships are not appropriate. It would be interesting to see how less-restricted reduced models (e.g., linear models such as the PLLM or PA-CDM) will perform under similar context in future studies, when an estimation algorithm is available for those models.

TABLE 7

Table 7. Model-data fit comparisons between the saturated and reduced models.

Discussion

Although considerable developments have been added to the CDM literature recently, most have been conducted for dichotomous responses only. Without a comprehensive modeling framework for polytomous responses, the advance of CDMs cannot be fully appreciated by applied researchers and practitioners across a wide range of areas. This research proposes a general cognitive diagnosis model for polytomous responses, which split the polytomous items indirectly based on the difference-between-category approach. The GPDM can be regarded as a natural extension of the G-DINA model, and the MML estimation is implemented using an EM algorithm. Under the GPDM framework, different saturated forms, and some reduced forms, can be transformed linearly. Model assessment and adjustment under the context of polytomous responses can proceed with the simulation- and residual-based method using the correlation of item pairs. The simulation study demonstrated the effectiveness of the model, especially when compared to dichotomizing polytomous responses with the G-DINA model. The improvement of classification accuracy of the attribute vector was dramatic with the use of the GPDM. Note that the number of items was more influential than the sample size on classification accuracy. This seems to be a good news for practitioners as increasing the number of items administered is usually more controllable in practice. Some item parameters of reduced CDMs for polytomous responses can be also recovered well with the GPDM. The real-data example further illustrated how the GPDM can make a difference in practice by providing additional diagnostic information and contributing to item development.

Although the GPDM appears to be promising, some issues should be addressed in future research for the framework to be more comprehensive and versatile. First, various reduced forms are subsumed under the framework and it would be useful to study some reduced CDMs in more details. As the number of response categories increases, the GPDM gets more complex, with a large number of parameters, where reduced models have fewer parameters and hence require smaller sample sizes for accurate estimation. Reduced models also have more straightforward interpretation of the attribute-item relationships when the models fit the data. In this regard, it would be helpful to investigate how various reduced models can effectively be estimated and compared within the general framework. Second, it would be valuable to assess whether Q-matrix validation procedures under the dichotomous context can be extended to polytomous responses, as Q-matrix plays a critical role in CDM-based measurement. It is also useful extend efficient and exhaustive search algorithm similar to the general method based on the discrimination index (de la Torre and Chiu, 2015) to polytomous responses. Third, the GPDM represents a specific approach to modeling polytomous responses. It would be interesting to compare other approaches of modeling to see how they could differ. Moreover, it is desirable to develop CDMs that can accommodate various response formats already covered under the IRT context (e.g., nominal, forced choice, graded unfolding), which can offer applied researchers a new perspective to re-conceptualize their research. Finally, the current treatment of the issue tended to be statistically oriented and compact. It would be desirable to have a didactic companion expanding and illustrating the modeling processes and procedures of model assessments and adjustments for practitioners. This would be especially useful when effective estimation methods for various reduced models are available.

Author Contributions

JC was responsible for most parts of the research, while JdlT helped with the introduction and discussion parts.

Funding

This work was supported by the Open Fund of National Higher Education Quality Monitoring Data Center (Higher Education Research Institute), Sun Yat-sen University. Grant number: M1803 and also supported by the Guangdong Province Philosophy and Social Science Planning Project. Grant number: GD17HJY01.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2018.01474/full#supplementary-material

Footnotes

1. ^The updated estimation code in Ox is available from the first author.

References

Akaike, H. (1974). A new look at the statistical identification model. IEEE Trans. Automated Control 19, 716–723. doi: 10.1109/TAC.1974.1100705

CrossRef Full Text | Google Scholar

Chen, H., and Chen, J. (2015). Exploring reading comprehension skill relationships through the G-DINA model. Educ. Psychol. 36, 1049–1064. doi: 10.1080/01443410.2015.1076764

CrossRef Full Text | Google Scholar

Chen, H., and Chen, J. (2016). Retrofitting non-cognitive-diagnostic reading assessment under the generalized DINA model framework. Lang. Assess. Q. 13, 218–230. doi: 10.1080/15434303.2016.1210610

CrossRef Full Text | Google Scholar

Chen, J. (2017). A residual-based approach to validate Q-matrix specifications. Appl. Psychol. Meas. 41, 277–293. doi: 10.1177/0146621616686021

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., and de la Torre, J. (2013). A general cognitive diagnosis model for expert-defined polytomous attributes. Appl. Psychol. Meas. 37, 419–437. doi: 10.1177/0146621613479818

CrossRef Full Text | Google Scholar

Chen, J., de la Torre, J., and Zhang, Z. (2013). Relative and absolute fit evaluation in cognitive diagnosis modeling. J. Educ. Meas. 50, 123–140. doi: 10.1111/j.1745-3984.2012.00185.x

CrossRef Full Text | Google Scholar

Chen, J., and Zhou, H. (2017). Test designs and modeling under the general nominal diagnosis model framework. PLoS ONE 12:e0180016. doi: 10.1371/journal.pone.0180016

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiu, C.-Y. (2013). Statistical refinement of the Q-matrix in cognitive diagnosis. Appl. Psychol. Meas. 37, 598–618. doi: 10.1177/0146621613488436

CrossRef Full Text | Google Scholar

Chiu, C.-Y., Douglas, J., and Li, X. (2009). Cluster analysis for cognitive diagnosis: theory and applications. Psychometrika 74, 633–665. doi: 10.1007/s11336-009-9125-0

CrossRef Full Text | Google Scholar

de la Torre, J. (2008). An empirically-based method of Q-matrix validation for the DINA model: development and applications. J. Educ. Meas. 45, 343–362. doi: 10.1111/j.1745-3984.2008.00069.x

CrossRef Full Text | Google Scholar

de la Torre, J. (2009). A cognitive diagnosis model for cognitively-based multiple-choice options. Appl. Psychol. Meas. 33, 163–183. doi: 10.1177/0146621608320523

CrossRef Full Text | Google Scholar

de la Torre, J. (2010). “The partial-credit DINA Model,” in Paper Presented at the International Meeting of the Psychometric Society (Athens).

de la Torre, J. (2011). The generalized DINA model framework. Psychometrika 76, 179–199. doi: 10.1007/s11336-011-9207-7

CrossRef Full Text | Google Scholar

de la Torre, J., and Chen, J. (2011). “Estimating different reduced cognitive diagnosis models using a general framework” inPaper Presented at the Annual Meeting of the National Council on Measurement in Education (New Orleans, LA).

de la Torre, J., and Chiu, C. Y. (2015). A General Method of Empirical Q-Matrix Validation. Psychometrika 81, 253–273. doi: 10.1007/s11336-015-9467-8

PubMed Abstract | CrossRef Full Text

de la Torre, J., and Douglas, J. (2004). A higher-order latent trait model for cognitive diagnosis. Psychometrika 69, 333–353. doi: 10.1007/BF02295640

CrossRef Full Text | Google Scholar

de la Torre, J., and Douglas, J. (2008). Model evaluation and multiple strategies in cognitive diagnosis: an analysis of fraction subtraction data. Psychometrika 73, 595–624. doi: 10.1007/s11336-008-9063-2

CrossRef Full Text | Google Scholar

Deely, J. J., and Lindley, D. V. (1981). Bayes empirical bayes. J. Am. Stat. Assoc. 76, 833–841. doi: 10.1080/01621459.1981.10477731

CrossRef Full Text | Google Scholar

DiBello, L., Roussos, L., and Stout, W. (2007). “Cognitive diagnosis Part I,” in Handbook of Statistics Psychometrics, Vol. 26, eds C. R. Rao and S. Sinharay (Amsterdam: Elsevier), 979–1030.

Doornik, J. A. (2003). Object-Oriented Matrix Programming Using Ox (Version 3.1) [Computer software]. London: Timberlake Consultants Press.

García, P. E., Olea, J., and de la Torre, J. (2014). Application of cognitive diagnosis models to competency-based situational judgment tests. Psicothema 26, 372–377. doi: 10.7334/psicothema2013.322

PubMed Abstract | CrossRef Full Text

Hartz, S. (2002). A Bayesian Framework for the Unified Model for Assessing Cognitive Abilities: Blending Theory with Practicality. Unpublished Doctoral Dissertation, University of Illinois at Urbana-Champaign.

Google Scholar

Henson, R. A., Templin, J., and Willse, J. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika 74, 191–210. doi: 10.1007/s11336-008-9089-5

CrossRef Full Text | Google Scholar

Hong, C.-Y., Chang, Y.-W., and Tsai, R.-C. (2016). Estimation of generalized DINA model with order restrictions. J. Classif. 33, 460–484. doi: 10.1007/s00357-016-9215-5

CrossRef Full Text | Google Scholar

Jang, E. E. (2009). Cognitive diagnostics assessment of L2 reading comprehension ability: validity arguments for fusion model application to LanguEdge assessment. Lang. Test. 26, 31–73. doi: 10.1177/0265532208097336

CrossRef Full Text | Google Scholar

Junker, B. W., and Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with non-parametric item response theory. Appl. Psychol. Meas. 25, 258–272. doi: 10.1177/01466210122032064

CrossRef Full Text | Google Scholar

Köhn, H. F., and Chiu, C. Y. (2016). A procedure for assessing the completeness of the Q-matrices of cognitively diagnostic tests. Psychometrika 82, 112–132. doi: 10.1007/s11336-016-9536-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, E. L., and Casella, G. (1998). Theory of Point Estimation. New York, NY: Springer Verlag.

Google Scholar

Ma, W., and de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses. Br. J. Math. Stat. Psychol. 69, 253–275. doi: 10.1111/bmsp.12070

PubMed Abstract | CrossRef Full Text | Google Scholar

Maris, E. (1999). Estimating multiple classification latent class models. Psychometrika 64, 187–212. doi: 10.1007/BF02294535

CrossRef Full Text | Google Scholar

Muraki, E. (1992). A generalized partial credit model: application of an EM algorithm. Appl. Psychol. Meas. 16, 159–176. doi: 10.1177/014662169201600206

CrossRef Full Text | Google Scholar

OECD (1999). Measuring Student Knowledge and Skills: A New Framework for Assessment. Paris: Organisation for Economic Co-operation and Development.

OECD (2006a). Assessing Scientific, Reading and Mathematical Literacy: A Framework for PISA 2006. Paris: Organisation for Economic Co-operation and Development.

OECD (2006b). PISA Released Items: Reading. Available online at: http://www.oecd.org/pisa/38709396.pdf

Rupp, A. A., Templin, J., and Henson, R. A. (2010). Diagnostic Measurement: Theory, Methods, and Applications. New York, NY: Guilford Press.

Samejima, F. (1969). Estimation of Latent Ability Using a Response Pattern of Graded Scores. New York, NY: Psychometric Society.

Google Scholar

Schwarzer, G. (1976). Estimating the dimension of a model. Ann. Stat. 6, 461–464. doi: 10.1214/aos/1176344136

CrossRef Full Text | Google Scholar

Tatsuoka, K. K. (1990). “Toward an integration of item-response theory and cognitive error diagnosis,” in Diagnostic Monitoring Skills and Knowledge Acquisition, eds N. Frederiksen, R. Glaser, A. Lesgold, and M. Safto (Hillsdale, NJ: Erlbaum), 453–488.

Google Scholar

Templin, J., Henson, R. A., Rupp, A. A., Jang, E., and Ahmed, M. (2008). “Cognitive diagnosis models for nominal response data,” in Paper Presented at the National Council on Measurement in Education (New York, NY).

Google Scholar

Templin, J. L., and Henson, R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models. Psychol. Methods 11, 287–305. doi: 10.1037/1082-989X.11.3.287

PubMed Abstract | CrossRef Full Text | Google Scholar

von Davier, M. (2008). A general diagnostic model applied to language testing data. Br. J. Math. Stat. Psychol. 61, 287–307. doi: 10.1348/000711007X193957

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, G., and Zhang, S. (2016). Identifiability of diagnostic classification models. Psychometrika 81, 625–649. doi: 10.1007/s11336-015-9471-z

PubMed Abstract | CrossRef Full Text | Google Scholar