- 1 Department of Horticulture and Landscape Architecture, Purdue University, West Lafayette, IN, USA
- 2 Department of Biology, Indiana/Purdue University Fort Wayne, Fort Wayne, IN, USA
The study of plant mutants with twisting growth in axial organs, which normally grow straight in the wild-type, is expected to improve our understanding of the interplay among microtubules, cellulose biosynthesis, cell wall structure, and organ biomechanics that control organ growth and morphogenesis. However, geometric constraints based on symplastic growth and the consequences of these geometric constraints concerning interpretations of twisted-organ phenotypes are currently underestimated. Symplastic growth, a fundamental concept in plant developmental biology, is characterized by coordinated growth of adjacent cells based on their connectivity through cell walls. This growth behavior implies that in twisting axial organs, all cell files rotate in phase around the organ axis, as has been illustrated for the Arabidopsis spr1 and twd1 mutants in this work. Evaluating the geometry of such organs, we demonstrate that a radial gradient in cell elongation and changes in cellular growth anisotropy must occur in twisting organs out of geometric necessity alone. In-phase rotation of the different cell layers results in a decrease of length and angle toward organ axis from the outer cell layers inward. Additionally, the circumference of each cell layer increases in twisting organs, which requires compensation through radial expansion or an adjustment of cell number. Therefore, differential cell elongation and growth anisotropy cannot serve as arguments for or against specific hypotheses regarding the molecular cause of twisting growth. We suggest instead, that based on mathematical modeling, geometric constraints in twisting organs are indispensable for the explanation of the causal connection of molecular and biomechanical processes in twisting as well as normal organs.
Introduction
Growth of cells in higher land plants is the irreversible deformation of the cell wall that is driven by the intracellular hydrostatic pressure (turgor) which the growing cells can maintain as long as an extracellular water source is available (Cosgrove, 2005). Hydrostatic pressure is an isotropic force; it acts indiscriminately in all directions. Therefore, the development of non-spherical cell shapes must be due to different degrees of cell wall extensibility in different directions (Peters et al., 2000). This results in growth along one or more predominant axes, a process termed anisotropic growth. This morphogenesis through anisotropic wall growth is thought to be regulated by the geometry of arrays of stress-bearing cellulose fibrils in the wall; it is widely accepted that irreversible cell wall enlargement proceeds perpendicularly to the orientation of those fibrils in higher plants (Baskin, 2005; Geitmann and Ortega, 2009). In turn, it is believed that cellulose fibril orientation is controlled by cortical microtubules (MT), which appear to guide the movement of active cellulose synthase complexes in the plasma membrane (Baskin, 2001; Paredez et al., 2006; Lloyd and Chan, 2008).
To obtain further insights into the regulation of cell, tissue, and organ expansion, mutants in which a known controlling component of development is affected and which show a clear morphogenetic phenotype are most welcome tools. Concerning the interplay of MTs, cellulose fibrils, and growth mechanics, a number of Arabidopsis mutants exhibiting twisted-organ phenotypes have attracted interest (for recent reviews, see Hashimoto, 2011, and Vaughn et al., 2011). In these lines, cell files of axial organs start to twist helically along the organ axis as their cells proceed through the growth process, and the organ rotates around its longitudinal axis (Furutani et al., 2000; Thitamadee et al., 2002). The mode of cell file orientation – left- or right-handed – seems fixed in some mutants including spiral1 and spiral2 (spr1 and spr2, from here on: “spr” unless further specified; Furutani et al., 2000; Buschmann et al., 2004; Sedbrook et al., 2004; Shoji et al., 2004; Nakajima et al., 2006; Yao et al., 2008) as well as lefty1 and lefty2 (Thitamadee et al., 2002; Abe et al., 2004), but is variable in other mutants such as twisted dwarf1 (twd1; Kamphausen et al., 2002; Pérez-Pérez et al., 2004; Figure 3). Most of the known twisted-organ mutants are mutated in tubulins or MT-associated proteins (MAPs; Furutani et al., 2000; Whittington et al., 2001; Thitamadee et al., 2002; Ishida et al., 2007; Perrin et al., 2007; Wang et al., 2007). For example, spr mutant phenotypes are caused by mutations in MAP genes (Buschmann et al., 2004; Nakajima et al., 2004; Sedbrook et al., 2004; Shoji et al., 2004), while the two lefty mutants exhibit the same amino acid substitution in two different α-tubulin isoforms of Arabidopsis (Thitamadee et al., 2002). In contrast, TWD1 is an FKBP-type immunophilin, shown to interact with ABC transporters (Geisler et al., 2003, 2004). Interacting ABC transporters of the ABCB subclass are essential for polar auxin efflux from cells (Bouchard et al., 2006). The TWD1 protein is localized to most major membrane systems, plasma membrane, tonoplast, and endoplasmic reticulum (Kamphausen et al., 2002; Geisler et al., 2003, 2004; Wu et al., 2010). In twd1 roots, ABCB transporters were mislocalized to the ER instead of the plasma membrane, apparently leading to disturbance of auxin flow patterns in the root growth zone (Wu et al., 2010). How these phenomena interact with MT dynamics, or whether they influence organ biomechanics through different routes remains obscure. Taken together, the examples mentioned demonstrate that twisting organ phenotypes may be evoked through a variety of molecular mechanisms. What are the mechanisms by which the distinct molecular causes converge on the same biomechanic result? To answer this question, understanding the biomechanical process of twisting growth is as important as understanding the underlying molecular causes.
In the current literature, there is only one explicit geometric model of the twisting growth process. Furutani et al. (2000) formulated a hypothesis on the developmental biomechanic origin of the twisted hypocotyl phenotype in Arabidopsis spr mutants, which was later expanded in theory to explain twisting phenotypes of any multicellular radial organ. Here we describe a model based on biomechanical principles to explain twisting (helical) organ growth.
The Current Helical Growth Model and Symplastic Growth
Proceeding from the periphery to the center of an Arabidopsis wild-type hypocotyl, one finds a single-layered epidermis, two layers of cortical parenchyma (outer and inner cortex), a single-layered endodermis, and finally the vascular tissues concentrated into a dense central bundle (Gendreau et al., 1997). In the mature stage, all cells are elongated but the cells of the two parenchymatic cortical layers show the largest radial diameters. Furutani et al. (2000) found that, in the spr1 mutant, the cells of the cortex and endodermis appeared shorter and wider than in the wild-type, whereas epidermal cells seemed unaffected. They concluded that the mutation had led to a loss of growth anisotropy in inner tissue cells, but not in the epidermis. Since the inner cells did not elongate as much as epidermal cells, and because this difference was not balanced by changes in the rate of cell production in the different tissue layers, the cell files of the epidermis had to wrap around the shortened inner tissues. The graphic representation of this idea by Furutani et al. (2000) has been reproduced practically unchanged by Hashimoto (2002, p. 806; 2011, p. 249) and by Ishida et al. (2007, p. 62); it is redrawn here as Figure 1.
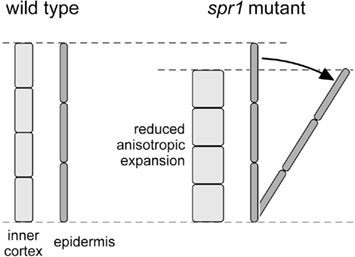
Figure 1. Geometric model of the interactions of tissues involved in twisting growth in Arabidopsis wild-type and spr1 hypocotyls; redrawn after Furutani et al. (2000, Fig. 11 on p. 4451). We cannot describe this graph any better than Hashimoto (2002, p. 806) did: “In the wild-type organ axis, the sum of inner cell length is equal to the sum of epidermal cell length, whereas inner cells of spiral mutant organs are defective in anisotropic growth and the total longitudinal length is shorter than that of epidermal cells. To compensate for this difference, the mutant epidermal cell files must skew.”
Taken at face value, Figure 1 shows how the epidermal cell files are tilted in relation to the organ axis while the underlying, radially expanded and shortened cell files do not, but are aligned with the organ axis. This implies that the epidermal cell layer is also tilted with respect to the underlying cell layer, which requires that cells slide past each other during the growth process. However, the movement of growing cells relative to their neighbors – so-called sliding growth – has been a controversial concept among the older botanists, mainly because it would have drastic physiological consequences including the loss of plasmodesmata-mediated symplastic continuity in growing tissues which, in fact, was never observed. A series of in-depth analyzes in the early twentieth century (Priestley, 1930; Sinnott and Bloch, 1939; Brumfield, 1942) led to the conclusion “that sliding growth does not occur” (Sinnott, 1939, p. 57). Plant tissues rather expand through what Priestley (1930) called symplastic growth: “a process in which the three-dimensional cell wall network adjusts to complex tension patterns as a common framework, without the necessity for any slip between any two cellulose walls facing one another across a common middle lamella” (Priestley, 1930, p. 102; for a discussion of terminological issues, see Erickson, 1986). Neighboring plant cells share a common cell wall, established during cell division with the formation of the cell plate, and perforated by plasmodesmata, which represent cytoplasmic channels that interconnect adjacent cells. These shared cell walls result in adjacent cells growing as a symplastic unit. Symplastic growth is the basis of the statement found, in this form or another, in every modern text-book of plant cell and developmental biology: “plant cells are surrounded by a framework of relatively rigid cell walls. There is therefore virtually no cell migration in plants, and major changes in the shape of the developing plant cannot be achieved by the movement and folding of sheets of cells” (Wolpert et al., 2007). Concerning twisting growth, the symplastic mode of growth requires that the organ twists as a whole, forcing us to postulate that all cell layers of the entire organ, not only the epidermis, twist in phase around the longitudinal axis of the organ. In other words, we claim that if an epidermal cell file completes a rotation of 360° around the organ axis over a given distance of organ length, then all other cell files will complete the same rotation as well.
In-Phase Rotation of Various Cell Layers and How it Shows
Whether all cell files twist in phase in twisting organs could be addressed in a visually impressive way by presenting 3D-reconstructions of confocal laser-scanning micrograph stacks. However, we purposefully employed a low-tech/low-cost/low-res approach which can easily be replicated by means of standard light microscopy. Figure 2A shows an etiolated spr1 hypocotyl; focal depth is minimized, and the focal plane lies in the longitudinal mid-plane of the organ. Epidermis (E), the outer and inner cortical parenchyma layers (Co, Ci), endodermis (N), and the vascular system (V) are visible. The relative sizes of the cells of the different tissues appear to be in agreement with the report by Furutani et al. (2000). As the focal plane is moved upward, we consecutively focus on Ci (Figure 2B), Co (Figure 2C), and E (Figure 2D); File S1 in Supplementary Material shows the moving focal plane. The positions on the organ mid-plane that correspond to the focal planes in Figure 2B–D are indicated at the bottom of Figure 2A. Evidently, the longitudinal cell walls of all tissues are skewed with respect to the organ axis, which for geometric reasons does not show in radial longitudinal sections such as Figure 2A, but does in tangential ones (Figures 2B–D). The only exceptions are cell files which revolve around the organ axis at such a small radius that the complete helical file is included in the focal plane. This is the case with the xylem vessels in the vascular tissue which are easily identified due to their spiral wall reinforcements (Figure 2A). At the position indicated by the filled arrowhead at the left margin of Figure 2A, these vessels are lined up in the direction of view. As a result, the xylem appears as one narrow band. At the positions highlighted by open arrowheads, several xylem vessels can be seen lying in parallel with each other in the optical plane. Clearly, the vessels twist in relation to the organ axis, forming helices with very small radii. The frequency of rotation of such a helix can be expressed as the distance along the organ axis over which the cell file covers a full circle of 360°. Compared to the radii of the xylem helices, their frequencies of rotation are huge (several hundreds of μm). Consequently, the pitch of the xylem helices, expressed as the angle between the longitudinal axes of the cells and the organ axis, is small to the point of being difficult to measure reliably. On the other hand, the angles between the organ axis and the longitudinal walls of Ci, Co, and E cells can be more reproducibly determined in tangential longitudinal focal planes, where the organ axis is conveniently indicated by the shadow of the vascular tissues in the background (Figures 2B–D). It is worth noting that the true pitch of the helical cell files shows only right above the strand of vascular tissues, i.e., in that radial mid-plane which includes the direction of view, because only there are the longitudinal axes of the cell files parallel to the focal plane. We measured the pitch (angle α) of several clearly visible cell walls (marked by circles in Figures 2B–D) and arrived at average values of 16° for Ci (Figure 2B), 28° for Co (Figure 2C), and 38° for E (Figure 2D). Evidently, the pitch angle α increases with the distance of each rotating cell file from the organ center, an observation already described by Furutani et al. (2000) but not further quantified or investigated. Moreover, we can determine the radii (r) of the helices described by the cell files for which we have established the pitch angles, either through estimating the relative positions of the focal planes of Figures 2B–D as indicated at the bottom of Figure 2A, or by calculating the radii from the positions of the individual images presented as Figures 2B–D in the original image stack (compare File S1 in Supplementary Material). Thus, we can compute the distance (d) along the organ axis over which every cell file completes one full 360° revolution around the organ axis, by using the formula d = 2rπ(tan α)−1. The mathematical background of this equation will be discussed in conjunction with Figure 4. For Ci, Co, and E, we arrive at d values of 960, 1130, and 1060 μm, respectively. Despite the rather crude methodology, these values are quite similar and indicate that the cell files of each tissue type are oriented helically around the organ axis with the same frequency, which in this example is approximately 1 mm−1. This result suggests that our postulate of there being no sliding growth and that, therefore, all cell files twist in phase around the organ axis, is valid.
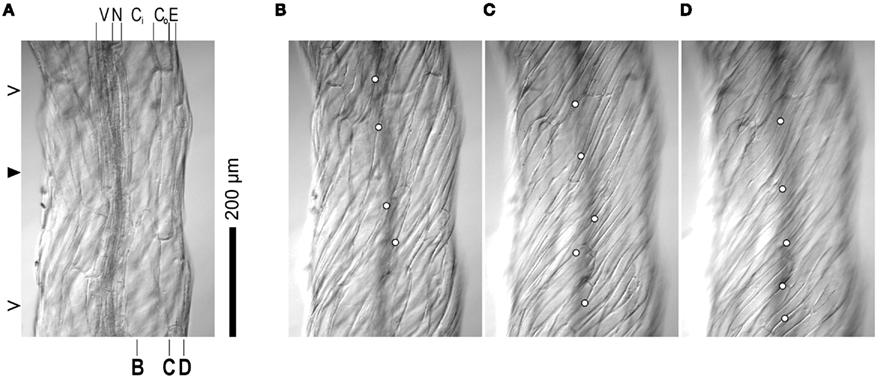
Figure 2. Light micrographs of an etiolated Arabidopsis spr1 mutant hypocotyl, taken with the focal plane in the organ mid-plane (A), the inner cortex (B), the outer cortex (C), and the epidermis (D). Identity of tissue layers are indicated on top of (A) (V, vascular system; N, endodermis; Ci, inner cortex; Co, outer cortex; E, epidermis). The approximate positions of the focal planes of (B–D) relative to the various cell layers is marked at the bottom of subfigure (A). Closed and open arrowheads on the left of (A) highlight regions in which xylem strands are either lined up in the direction of view (closed) or lie parallel with each other in the optical plane, respectively, (open) causing the xylem to appear as two separate strands. Circles in (B–D) identify longitudinal cell walls used for pitch measurements. The micrographs shown are elements of the image stack presented as File S1 in Supplementary Material. Plants were grown on half strength MS, 1% sucrose medium at 22°C in the dark for 7 days. Images were captured with a Micropublisher 5.0 RTV CCD camera (QImaging, Surrey, BC, Canada) on a Vanox microscope (Olympus Imaging America Inc., Center Valley, PA, USA).
The very fact of in-phase rotation holds the key to the proper understanding of cell and tissue geometry in twisting organs. Irregularities such as kinks in the tissues, narrowing and widening of individual cell files, spontaneous or tropic curvatures of the organ, and elastic tensions in live tissues frequently obscure the general pattern, which nonetheless always holds. Figure 3 shows a twd1 root photographed with focal planes in the organ mid-plane, the root cortex, and the root epidermis, respectively. The molecular mechanisms that ultimately underlie the twisting phenotype are different in twd1 and spr1, and the direction of cell file orientation is fixed in spr1 but variable in twd1. Nevertheless, the postulate holds in twd1 roots just as it does in spr1 hypocotyls: all cell files twist in phase.
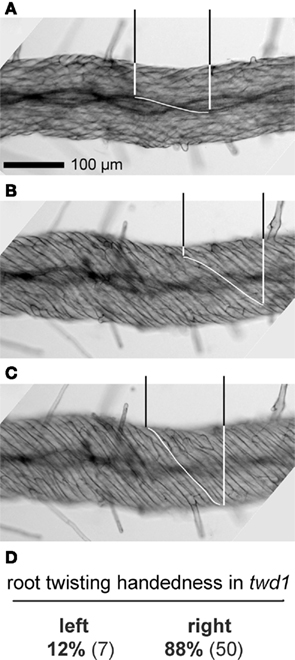
Figure 3. Light micrographs of an Arabidopsis twd1 root, taken with the focal plane in the organ mid-plane (A), the parenchymal root cortex (B), and the epidermis (C). The pitch of the helically rotating cell files increases from the organ center toward the periphery. In each micrograph, the distance along the organ axis required by a cell file (xylem strands in (A), cortical parenchyma in (B), epidermal cells in (C)) to complete a semicircular rotation of 180° is highlighted for one exemplary file. These distances are practically identical in (A–C), indicating that all cell files twist in phase around the organ axis. (D) Handedness of root twisting in twd1 observed in the first 3 mm of the root tip. Roots were stained with Toluidine blue; other experimental details as in Figure 2.
Geometric Constraints in Twisting Organs
To fully appreciate the geometric relationships between cell layers in a twisting axial organ in the absence of sliding growth, we have to realize that if two helices of different radii wind concentrically as well as in phase around a common axis, the helix with the smaller radius will be steeper. For this reason, the angle between cell files and the axis of a twisted-organ decreases in a predictable way from the periphery toward the organ center (Figures 2–4). Moreover, steeper spirals are shorter relative to their axis of rotation than flatter ones. In axial plant organs, cell layers can be thought of as cylinders of different radii (r) which, in a thought experiment, can be cut open and unrolled to form rectangles with side lengths d (length of the cylinder along the organ axis, A) and 2rπ, the circumference of the cylinder (Figure 4). If d equals the distance along the organ axis (A) which cell files require for completion of a full rotation of 360°, the cell files will be represented by the diagonals of the rectangles. The dependence of cell file length on the radius of the cylindrical cell layer is obvious (Figure 4). We cannot claim originality for these insights which, in fact, had been expounded on in considerable detail by Nägeli and Schwendener(1877, p. 415–417) amongst other classical plant biologists. We wish to emphasize, however, that the radial gradients in cell file length and pitch reflect geometric constraints: the lengths and pitches of cell files in a twisting axial organ change in predictable ways along the radial organ axis, not because of some genetic specification, but out of biomechanical necessity.
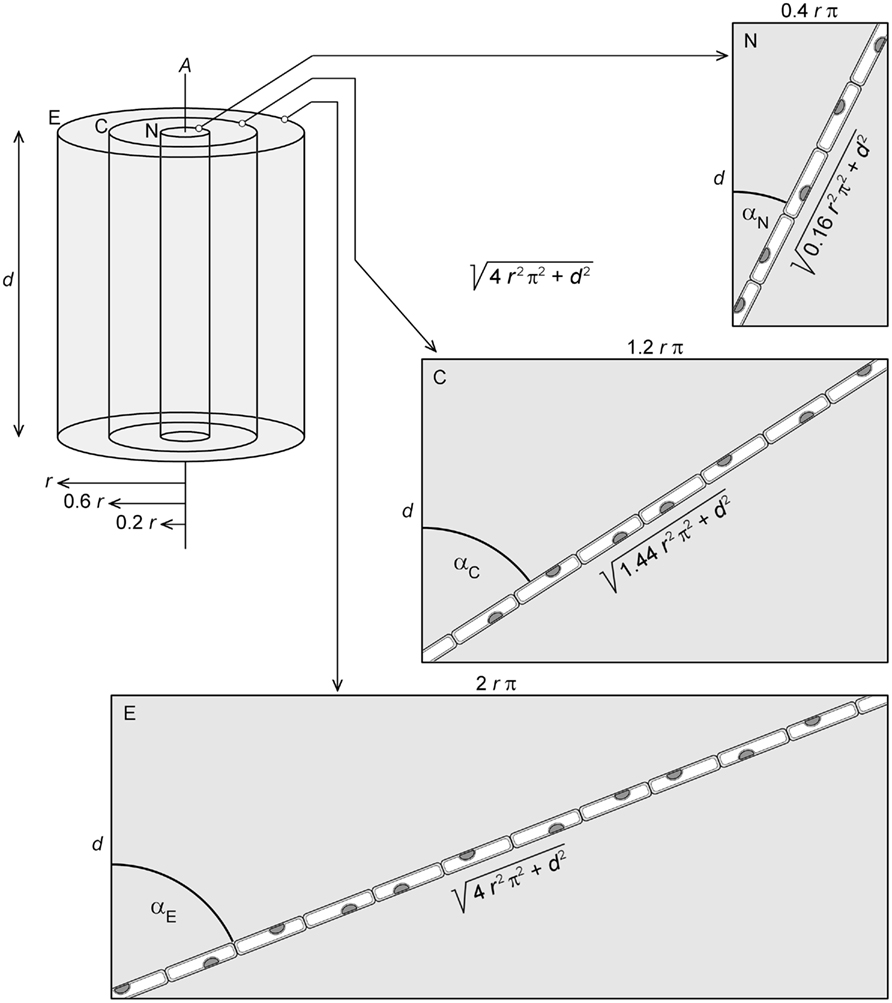
Figure 4. Thought experiment in which segments of axial length d of three cell layers of different radii (E, epidermis of radius r; C, cortex of radius 0.6 r; N, endodermis of radius 0.2 r) are isolated from a twisted-organ and cut open to form rectangles. If d is chosen to equal the distance along the organ axis (A) that the cell files require to complete one revolution around A, the length of each cell file will correspond to the diagonals of the respective rectangles. With d and r known, application of Pythagoras’ theorem yields cell file length. Note that cell file length and pitch angle α decrease toward the center of the organ.
It appears that any mutation or compound that reduces elongation in the organ center more strongly than in the periphery has the potential to generate twisting organ phenotypes. Does this mean that there is no role for the postulated cause of organ twisting in the original model (Figure 1), namely changes in cellular geometry and thus growth anisotropy? In the absence of changes in cell number, changes in cellular geometric and growth anisotropy must occur when an organ twists, out of geometric necessity. Consider a cross-section perpendicular to the longitudinal axis (A) of an axial organ in which elongated cells are organized in layers that represent cylinders with axes parallel to the organ axis. The geometry of the cells in this cross-section can be characterized by their tangential and radial diameters, ct and cr, respectively (Figure 5A). The sum of all individual ct values in one cell layer provides the central circumference of this tissue cylinder. Similarly, the organ radius equals the sum of the radial diameters (cr) of all cell layers (Figure 5A). If the model organ is growing straight with all longitudinal cell axes parallel to organ axis A (Figure 5B), ct and cr determined on an organ cross-section will be the actual tangential and radial diameters of the cells. What will happen if the organ starts to twist with constant cell number and unchanged cell anisotropy, that is, if all cell files wind helically around the organ axis without changes in ct and cr? The apparent tangential diameter of a cell in an organ cross-section will not be the true ct anymore, but ct(cos α)−1, where α is the pitch angle of the cell file (Figure 5C). This apparent tangential diameter is larger than ct for all possible pitch angles other than 0°. In other words, the projection of ct of a skewed cell onto the organ cross-sectional plane is larger than ct. Consequently, the circumference of a twisted cell cylinder – which is approximately the sum of all individual ct(cos α)–1 values in this cell layer – is larger than the circumference of the same cylinder before the twist. As a result, the circumference of the organ necessarily increases as the organ twists while the number and true tangential diameters of cells remain constant. On the other hand, the radial cell diameters (cr) on cross-sectional planes are unaffected when cell files skew with respect to the organ axis (Figure 5C). Because the organ radius (r) is the sum of the cell layers’ cr, r does not change when the organ twists. This, however, is paradoxical as the organ cannot increase in circumference while retaining the same radius.
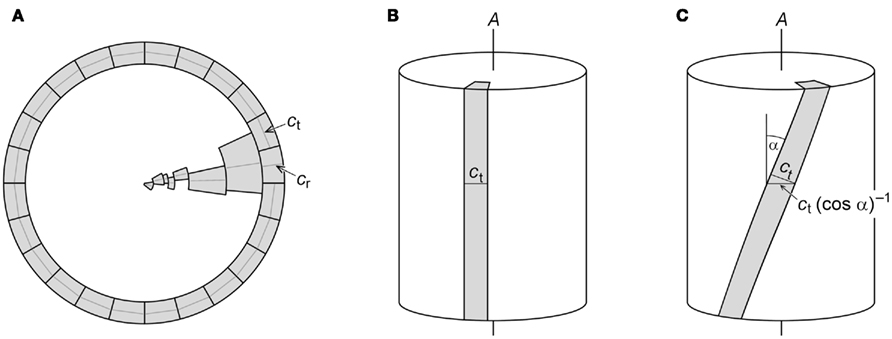
Figure 5. Models used to evaluate the consequences of twisting growth in the absence of changes in cell geometric anisotropy. (A) Schematic cross-section perpendicular to the longitudinal axis of an axial organ. The outermost cell layer and one cell from each of the inner cell layers are drawn. Centrally positioned transversal diameters (ct) of outer cells and radial diameters (cr) of each cell layer are indicated. The sum of all individual ct of a cell layer provides the central circumference of that layer, while the sum of the cr of all cell layers equals the organ radius. (B) If the longitudinal axis of a cell is parallel with the organ axis A, the ct measured on an organ cross-section represents the actual ct of the cell. (C) If a cell file is tilted with pitch angle α against A, the apparent ct measured on an organ cross-section overestimates the true ct by the factor (cos α)−1.
There are three modifications of the premises of our model that could avoid the paradox. The first possibility is that changes in cell (file) number could reduce the organ circumference and/or increase organ radius as required. Secondly, the true tangential diameters of the cells, ct, could decrease proportionally with the organ twist so that organ circumference and diameter remain constant in the process. In this case, cells actually would shrink tangentially and increase their geometric anisotropy as the organ twists. As a third possibility, at least some of the inner cells could expand radially – in other words, increase their cr – to provide the increase in organ radius required by the increase of organ circumference due to organ twisting. These cells would decrease their geometric anisotropy as they would grow wider relative to their length.
It is unlikely that changes in the number of cells or cell files are involved in twisting organs. The number of cell files is predetermined in the meristematic zone of the organ, whereas the cell files orient helically not before onset of rapid elongation. The cross-sections of wild-type and spr1 mutant hypocotyls that accompanied previous presentations of the model presented in Figure 1 (Furutani et al., 2000, p. 4451; Hashimoto, 2002, p. 806; Ishida et al., 2007, p. 62; Hashimoto, 2011, p. 249) show mutant hypocotyls of about twice the diameter and circumference of the wild-type organ. Nonetheless, cell file numbers are practically identical for each tissue type in wild-type and spr1 hypocotyls. Evidently, the first possibility is not realized, implying that changes in cell anisotropy must occur when organs twist. The second possibility, tangential shrinkage of cells, so far also lacks supporting evidence. We have quantified the tangential diameters of epidermal cells of spr1-6 (19.50 ± 1.55μm), twd1-1 (17.32 ± 2.59μm), and respective wild-type (Col-0: 20.05 ± 1.65μm, Ws-2: 17.66 ± 2.12μm) etiolated hypocotyls and found no significant differences between the three genotypes [Student t-test: spr1-6 and Col-0: p = 0.187, twd1-1 and Ws-2: p = 0.427 (n > 100 for all measurements)]. Similarly, tangential cell widths seem unaffected in lefty1 and lefty2 (Thitamadee et al., 2002). We are left with possibility three – the radial expansion of at least some inner cells. There is ample evidence demonstrating that this phenomenon occurs in real twisting organs, and it actually forms the basis of the model in Figure 1. It cannot be overstressed, though, that in the absence of changes of cell (file) number and tangential cell shrinkage, the radial expansion of inner cells is a geometric necessity. The fact that inner cells do expand radially in twisting organs cannot establish that the twist is caused by the radial expansion, since the radial expansion would occur as a necessary adjustment to the increased organ circumference in any case.
Some twisting organ mutants such as tua5D251N (Ishida et al., 2007) exhibit decreased anisotropy in the epidermal layer, resulting in tangentially wider cells. In affected axial organs, the tangential cell growth further promotes the increase of organ circumference, and thus amplifies the requirement for inner cells to expand radially.
We conclude that increased radial cell expansion is not a mandatory consequence of specific cell shape changes directed by cytoskeleton or cell wall architecture, but is based on geometric constraints within a twisting organ. This does not mean that cytoskeleton and cell wall architecture are irrelevant. Twisting growth can only occur if the radial cell walls are structured in such a way that the changes of cell shape required for twisting growth are possible. As implicated by several mutants, both cytoskeleton and cell wall architecture determine the handedness of twisting growth (Furutani et al., 2000; Buschmann et al., 2004; Sedbrook et al., 2004; Shoji et al., 2004; Nakajima et al., 2006; Yao et al., 2008).
Conclusion
When we consider biological objects, and especially when we move between levels of organization, we sometimes over-generalize our theories of fundamental biological processes, correct as they may be in principle. Knowing that higher plants consist of cells, and that cellular processes control properties of the multicellular entity, we tend to take it for granted that changes in cell shape are causes rather than effects of changing patterns of organ expansion. But this assumption can be misleading, as the example of twisting growth shows. The occurrence of radial gradients of cell file length and increased radial cell diameters in twisting organs reflects geometric constraints. These features must occur in twisting organs with any molecular or cellular mechanism that causes twisting growth, and therefore cannot be interpreted as evidence in favor of a particular one.
Let us clarify our conclusion by a hypothetical example. Imagine a twisting root mutant in which the length of the helical cell files of the epidermis between the apex and the first root hairs were shown to be identical to that of the straight cell files in the wild-type. In such a root, the lengths of the cell files will be found to decrease toward the organ center in a predictable way (Figure 4). If one assumes that there must be a direct correlation between molecular cause and cellular effect, one will conclude that the molecular mechanism through which the mutation reduces cell elongation is most active in the central cylinder, strongly active in the endodermis, somewhat active in the cortex, and inactive in the epidermis. However, the mutation could cause nothing but, for example, premature lignification of xylem vessels, which would prevent further organ elongation and might result in organ twisting due to the continuing tendency of non-xylem cells to expand. If so, every cell will elongate less than its peripheral neighbor, not because of differential molecular activities, but because of the system’s inherent geometric constraints.
Testing the model by Furutani et al., 2000; Figure 1), Nakajima et al., 2004 (2004, p. 1188) found via Northern blot analysis that SPR1 is expressed uniformly in all organs. Subsequent expression analysis using SPR1-promoter-GUS transgenic plants did not allow a detailed analysis of SPR1 in individual cell files of roots. These results “did not provide experimental data for this model” according to Nakajima et al. (2004). A similar lack of organ-specificity was detected for SPR2 expression (Buschmann et al., 2004). Nakajima et al. (2004) further concluded that “a complex non-cell-autonomous mechanism is behind the helical growth phenotype,” and that “extensive analysis” of gene expression patterns were “necessary to elucidate the complex mechanism.” As an alternative, we suggest that the essential non-cell-autonomous mechanisms that explain the geometry of helical organ growth are mechanic rather than genetic and originate from geometric constraints that follow from the fact that plant tissues expand by symplastic growth.
Author Contributions
Renate Weizbauer designed and conducted experiments, analyzed data, and wrote the manuscript, Winfried S. Peters designed experiments, analyzed data, performed mathematical modeling, and wrote the manuscript, Burkhard Schulz designed experiments, analyzed data, and wrote the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank M. Gudo, M. Gutmann, B. Herkner, D. Mollenhauer, D. S. Peters, and M. Weingarten for helpful discussion of the nature of constructional constraints, and M. Poling and R. Altstatt for critical reading and copy editing of the manuscript. This work was supported by startup funds from the Department of Horticulture and Landscape Architecture, Purdue University to Burkhard Schulz, Renate Weizbauer was supported by a Purdue University Bilsland fellowship.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/Plant_Physiology/10.3389/fpls.2011.00062/abstract
File S1. QuickTime movie file showing the microscope focal plane moving through an Arabidopsis spr1 mutant hypocotyl; corresponds to Figure 2. The movie is viewed best with the “Loop back and forth” option activated.
References
Abe, T., Thitamadee, S., and Hashimoto, T. (2004). Microtubule defects and cell morphogenesis in the lefty1lefty2 tubulin mutant of Arabidopsis thaliana. Plant Cell Physiol. 45, 211–220.
Baskin, T. I. (2001). On the alignment of cellulose microfibrils by cortical microtubules: a review and a model. Protoplasma 215, 150–171.
Baskin, T. I. (2005). Anisotropic expansion of the plant cell wall. Annu. Rev. Cell Dev. Biol. 21, 203–222.
Bouchard, R., Bailly, A., Blakeslee, J. J., Oehring, S. C., Vincenzetti, V., Lee, O. R., Paponov, I., Palme, K., Mancuso, S., Murphy, A. S., Schulz, B., and Geisler, M. (2006). Immunophilin-like TWISTED DWARF1 modulates auxin efflux activities of Arabidopsis P-glycoproteins. J. Biol. Chem. 281, 30603–30612.
Brumfield, R. T. (1942). Cell growth and division in living root meristems. Am. J. Bot. 29, 533–543.
Buschmann, H., Fabri, C. O., Hauptmann, M., Hutzler, P., Laux, T., Lloyd, C. W., and Schäffner, A. R. (2004). Helical growth of the Arabidopsis mutant tortifolia1 reveals a plant-specific microtubule-associated protein. Curr. Biol. 14, 1515–1521.
Furutani, I., Watanabe, Y., Prieto, R., Masukawa, M., Suzuki, K., Naoi, K., Thitamadee, S., Shikanai, T., and Hashimoto, T. (2000). The SPIRAL genes are required for directional control of cell elongation in Arabidopsis thaliana. Development 127, 4443–4453.
Geisler, M., Girin, M., Brandt, S., Vincenzetti, V., Plaza, S., Paris, N., Kobae, Y., Maeshima, M., Billion, K., Kolukisaoglu, H. Ü., Schulz, B., and Martinoia, E. (2004). Arabidopsis immunophilin-like TWD1 functionally interacts with vacuolar ABC transporters. Mol. Biol. Cell 15, 3393–3405.
Geisler, M., Kolukisaoglu, H. Ü., Bouchard, R., Billion, K., Berger, J., Saal, B., Frangne, N., Koncz-Kálmán, Z., Koncz, C., Dudler, R., Blakeslee, J. J., Murphy, A. S., Martinoia, E., and Schulz, B. (2003). TWISTED DWARF1, a unique plasma membrane-anchored immunophilin-like protein, interacts with Arabidopsis multidrug resistance-like transporters AtPGP1 and AtPGP19. Mol. Biol. Cell 14, 4238–4249.
Geitmann, A., and Ortega, J. K. E. (2009). Mechanics and modeling of plant cell growth. Trends Plant Sci. 14, 467–478.
Gendreau, E., Traas, J., Desnos, T., Grandjean, O., Caboche, M., and Höfte, H. (1997). Cellular basis of hypocotyl growth in Arabidopsis thaliana. Plant Physiol. 114, 295–305.
Hashimoto, T. (2002). Molecular genetic analysis of left-right handedness in plants. Phil. Trans. R. Soc. Lond. B Biol Sci. 357, 799–808.
Hashimoto, T. (2011). “Microtubule and cell shape determination,” in The Plant Cytoskeleton. Advances in Plant Biology, 2nd Edn, ed. B. Liu (Berlin: Springer), 245–257.
Ishida, T., Thitamadee, S., and Hashimoto, T. (2007). Twisted growth and organization of cortical microtubules. J. Plant Res. 120, 61–70.
Kamphausen, T., Fanghänel, J., Neumann, D., Schulz, B., and Rahfeld, J. U. (2002). Characterization of Arabidopsis thaliana AtFKBP42 that is membrane-bound and interacts with Hsp90. Plant J. 32, 263–276.
Lloyd, C. W., and Chan, J. (2008). The parallel lives of microtubules and cellulose microfibrils. Curr. Opin. Plant Biol. 11, 641–646.
Nakajima, K., Furutani, I., Tachimoto, H., Matsubara, H., and Hashimoto, T. (2004). SPIRAL1 encodes a plant-specific microtubule-localized protein required for directional control of rapidly expanding Arabidopsis cells. Plant Cell 16, 1178–1190.
Nakajima, K., Kawamura, T., and Hashimoto, T. (2006). Role of the SPIRAL1 gene family in anisotroic growth of Arabidopsis thaliana. Plant Cell Physiol. 47, 513–522.
Paredez, A. R., Somerville, C. R., and Ehrhardt, D. W. (2006). Visualization of cellulose synthase demonstrates functional association with microtubules. Science 312, 1491–1495.
Pérez-Pérez, J., Ponce, M. R., and Micol, J. L. (2004). The ULTRACURVATA2 gene of Arabidopsis encodes an FK506-binding protein involved in auxin and brassinosteroid signaling. Plant Physiol. 134, 101–107.
Perrin, R. M., Wang, Y., Yuen, C. Y., Will, J., and Masson, P. H. (2007). WVD2 is a novel microtubule-associated protein in Arabidopsis thaliana. Plant J. 49, 961–971.
Peters, W. S., Hagemann, W., and Tomos, A. D. (2000). What makes plants different? Principles of extracellular matrix function in ‘soft’ plant tissues. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 125, 151–167.
Priestley, J. H. (1930). Studies in the physiology of cambial activity. II. The concept of sliding growth. New Phytol. 29, 96–140.
Sedbrook, J. C., Ehrhardt, D. W., Fisher, S. E., Scheible, W. R., and Somerville, C. (2004). The Arabidopsis SKU6/SPIRAL1 gene encodes a plus end-localized microtubule-interacting protein involved in directional cell expansion. Plant Cell 16, 1506–1520.
Shoji, T., Narita, N. N., Hayashi, K., Asada, J., Hamada, T., Sonobe, S., Nakajima, K., and Hashimoto, T. (2004). Plant-specific microtubule-associated protein SPIRAL2 is required for anisotropic growth in Arabidopsis. Plant Physiol. 136, 3933–3944.
Sinnott, E. W. (1939). Growth and differentiation in living plant meristems. Proc. Natl. Acad. Sci. U.S.A. 25, 55–58.
Sinnott, E. W., and Bloch, R. (1939). Changes in intercellular relationships during the growth and differentiation in living plant tissues. Am. J. Bot. 26, 625–634.
Thitamadee, S., Tuchihara, K., and Hashimoto, T. (2002). Microtubule basis for left-handed helical growth in Arabidopsis. Nature 417, 193–196.
Vaughn, L. M., Baldwin, K. L., Jia, G., Verdonk, J. C., Strohm, A., and Masson, P. H. (2011). “The cytoskeleton and root growth behavior,” in The Plant Cytoskeleton. Advances in Plant Biology, 2nd Edn, ed. B. Liu (Berlin: Springer), 307–326.
Wang, X., Zhu, L., Liu, B., Wang, C., Jin, L., Zhao, Q., and Yuan, M. (2007). Arabidopsis microtubule associated protein18 functions in directional cell growth by destabilizing cortical microtubules. Plant Cell 19, 877–889.
Whittington, A. T., Vugrek, O., Wei, K. J., Hasenbein, N. G., Sugimoto, K., Rashbrooke, M. C., and Wasteneys, G. O. (2001). MOR1 is essential for organizing cortical microtubule in plants. Nature 411, 610–613.
Wolpert, L., Jessell, T., Lawrence, P., Meyerowitz, E., Robertson, E., and Smith, J. (2007). Principles of Development, 3rd Edn. Oxford: Oxford University Press.
Wu, G., Otegui, M. S., and Spalding, E. P. (2010). The ER-localized TWD1 immunophilin is necessary for localization of multidrug resistance-like proteins required for polar auxin transport in Arabidopsis roots. Plant Cell 22, 3295–3304.
Keywords: Arabidopsis thaliana, developmental biomechanics, spiral1 (spr1) mutant, symplastic growth, tissue geometry, tissue tension, twisted dwarf1 (twd1) mutant, twisting growth
Citation: Weizbauer R, Peters WS and Schulz B (2011) Geometric constraints and the anatomical interpretation of twisted plant organ phenotypes. Front. Plant Sci. 2:62. doi: 10.3389/fpls.2011.00062
Received: 29 June 2011;
Accepted: 14 September 2011;
Published online: 13 October 2011.
Edited by:
Jan Traas, UMR INRA–CNRS–ENSL–UCBL, FranceCopyright: © 2011 Weizbauer, Peters and Schulz. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Burkhard Schulz, Department of Horticulture and Landscape Architecture, Purdue University, 625 Agriculture Mall Drive, West Lafayette, IN 47907, USA. e-mail:YnNjaHVsekBwdXJkdWUuZWR1


