- Bioengineering Laboratory, Department of Mechanical Engineering, University of Colorado Denver, Denver, CO, USA
Regulation of cell growth is paramount to all living organisms. In plants, algae and fungi, regulation of expansive growth of cells is required for development and morphogenesis. Also, many sensory responses of stage IVb sporangiophores of Phycomyces blakesleeanus are produced by regulating elongation growth rate (growth responses) and differential elongation growth rate (tropic responses). “Stiff” mutant sporangiophores exhibit diminished tropic responses and are found to be defective in at least five genes; madD, E, F, G, and J. Prior experimental research suggests that the defective genes affect growth regulation, but this was not verified. All the growth of the single-celled stalk of the stage IVb sporangiophore occurs in a short region termed the “growth zone.” Prior experimental and theoretical research indicates that elongation growth rate of the stage IVb sporangiophore can be regulated by controlling the cell wall mechanical properties within the growth zone and the magnitude of the turgor pressure. A quantitative biophysical model for elongation growth rate is required to elucidate the relationship between wall mechanical properties and turgor pressure during growth regulation. In this study, it is hypothesized that the mechanical properties of the wall within the growth zone of stiff mutant sporangiophores are different compared to wild type (WT). A biophysical equation for elongation growth rate is derived for fungal and plant cells with a growth zone. Two strains of stiff mutants are studied, C149 madD120 (−) and C216 geo- (−). Experimental results demonstrate that turgor pressure is larger but irreversible wall deformation rates within the growth zone and growth zone length are smaller for stiff mutant sporangiophores compared to WT. These findings can explain the diminished tropic responses of the stiff mutant sporangiophores. It is speculated that the defective genes affect the amount of wall-building material delivered to the inner cell wall.
Introduction
Regulation of cell growth is paramount to all living organisms. In plants, algae, and fungi, regulation of expansive growth of cells is required for development and morphogenesis. Expansive growth of plant, algal, and fungal cells (cells with walls) employ the same physical principles. The cell produces active solutes within the protoplast and absorbs water from its surroundings. The influx of water produces turgor pressure that stresses the cell wall. The wall deforms in response to the wall stresses generated by the turgor pressure. The wall deformation is reversible (elastic) for non-growing cells, and both elastic and irreversible for growing cells. Experimental evidence (Green, 1969; Richmond et al., 1980; Bartnicki-Garcia et al., 2000; Dumais et al., 2004; Baskin, 2005) and mathematical models (Gierz and Bartnicki-Garcia, 2001; Dumais et al., 2006; Goriely and Tabor, 2008; Geitmann and Ortega, 2009; Fayant et al., 2010) demonstrate that the shapes of cells with walls are determined by controlling the wall mechanical properties during expansive growth. Complicated growth behavior such as helical growth of the large single-celled sporangiophores of Phycomyces blakesleeanus, and the reversals in helical growth direction that occur during development and bulging, can also be explained by controlling the mechanical properties of the cell wall (Castle, 1942; Roelofsen, 1950; Ortega and Gamow, 1974; Ortega et al., 1974; Yoshida et al., 1980; Goriely and Tabor, 2011).
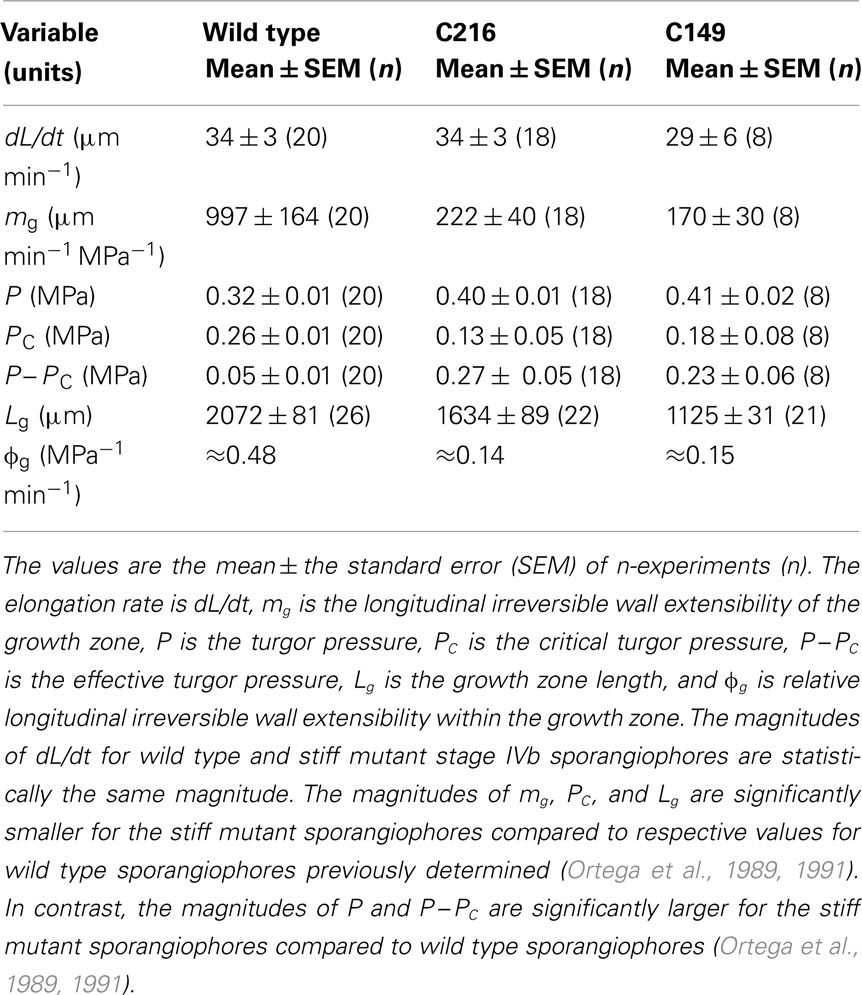
The sporangiophores of P. blakesleeanus are large, single cells that detect and respond to different environmental stimuli. Some of these stimuli are gravity, ethylene, mechanical stretch, gases, temperature, wind, light intensity, spatially asymmetric distribution of light, and the presence of solid objects (Bergman et al., 1969; Cerda-Olmedo and Lipson, 1987). The sporangiophores respond to all of these environmental and sensory stimuli with symmetric and asymmetric changes in growth rate. Typically, sporangiophores used for experimentation are obtained from vegetative spores (Bergman et al., 1969; Cerda-Olmedo and Lipson, 1987). When inoculated on a suitable growth medium, the spores germinate. Within a couple of days after germination, a mycelium is formed and aerial hyphae (sporangiophores) begin to grow vertically (upward). Sporangiophore development is divided into five stages: I, II, III, IV, and V (Figure 1), where stage IV is further divided into three sub-stages: IVa, IVb, and IVc (Bergman et al., 1969; Cerda-Olmedo and Lipson, 1987).
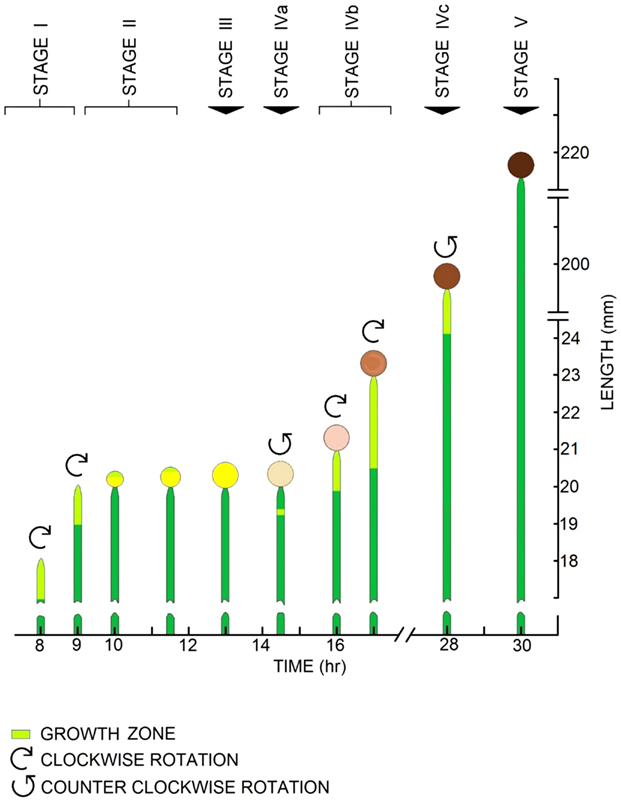
Figure 1. A schematic illustration of the developmental stages of Phycomyces blakesleeanus. Stage I sporangiophore appears as a single pointed tube that grows longitudinally at the apical tip in the growth zone. The growth zone is light green and the non-growing stalk is dark green. Clockwise rotation (when viewed from above) and elongation growth occur concurrently during stage I producing left-handed helical growth. Stage II begins with spherical growth at the apical tip without elongation and rotation growth. The diameter of the sporangium continues to increase until stage III, where the diameter is constant (≈0.5 mm). During stage III there is no visible growth. Stage IVa begins with elongation growth concurrent with counter-clockwise rotation growth (right-handed helical growth) in a short growth zone located approximately 0.6 mm below the sporangium. The sporangium begins to darken and elongation growth, rotation growth, and growth zone length continue to increase during this stage. The right-handed helical growth continues for approximately 1 h before the rotation rate gradually decreases to zero and clockwise rotation begins. Stage IVb begins with the initiation of left-handed helical growth. Stage IVb exhibits nearly constant elongation and rotation growth rates for many hours. Stage IVc is initiated by counter-clockwise rotation and right-handed helical growth. Typically, this is a very old sporangiophore. Stage V is the last stage and does not exhibit visible growth.
The stage I sporangiophore appears as a single pointed tube that grows longitudinally (Figure 1). All the growth occurs in a short zone (growth zone) between the apical tip and approximately 1.0 mm below it. In general, the mechanical extensibility of the cell wall in the growth zone is greater than in other regions of the sporangiophore stalk. The cell wall in the growth zone elongations (5–20 μm min−1) and twists in such a way that a small particle attached to the surface near the apical tip will rotate (≈30° h−1) in the clockwise direction when viewed from above, and trace out a left-handed helix in time and space (left-handed helical growth). Typically, the stage I sporangiophore reaches a length of 1–2 cm and a diameter of 0.15–0.20 mm near the mycelium.
In stage II, elongation and rotation cease and spherical growth begins at the apical tip (Figure 1). Within 3 h, a bright yellow spherical sporangium is formed (diameter ≈0.5 mm), after which spherical growth stops. In stage III, there is no visible growth (≈2 h in duration). Presumably, this is a period of active spore formation.
Stage IVa begins with elongation and counter-clockwise rotation in a short growth zone on the stalk located approximately 0.6 mm below the base of the sporangium (Figure 1). This right-handed helical growth continues for approximately 1 h before the rotation rate gradually decreases to zero and clockwise rotation begins. Stage IVb begins with the initiation of clockwise rotation and left-handed helical growth (Figure 1). Within an hour or two, the elongation rate, the rotation rate, and the length of the growth zone increase to somewhat constant and typical values of approximately 45 μm min−1, 12° min−1, and 2.5 mm, respectively, and are maintained for hours afterward. Typically, the elongation and rotation rates are measured at one end of the growth zone, usually at the non-growing sporangium, and represent the sum of all the elongation and rotation that occur throughout the length of the growth zone. Stage IVc begins with another reversal in rotation (Figure 1), to the counter-clockwise direction (right-handed helical growth). Stage IVc sporangiophores are long (>10 cm). Stage V sporangiophores are the final stage (Figure 1). They do not exhibit visible growth.
Most biophysical research is conducted with the stage IVb sporangiophore, which is a large cylindrical single-celled stalk (0.1–0.2 mm in diameter) with a spherical sporangium on top (approximately 0.5 mm in diameter) that contains spores for vegetative reproduction. The stalk elongates vertically, opposite to the gravitational acceleration (negatively geotropic), at a nearly constant rate that ranges between 35 and 60 μm min−1. All the growth occurs in a growth zone that is adjacent to the sporangium and typically 2–3 mm in length. The single-celled sporangiophore stalk can grow to a length greater than 20 cm.
Historically, the underlying mechanisms that produce and regulate elongation growth rate of the sporangiophores of P. blakesleeanus have been studied because the sporangiophores are used as a model system for investigations in sensory transduction (Bergman et al., 1969; Cerda-Olmedo and Lipson, 1987). Many sensory responses of stage IVb sporangiophores of P. blakesleeanus are produced by regulating the magnitude of the elongation growth rate (e.g., light growth response, avoidance growth response, house growth response, and stretch growth response) and regulating differential elongation growth rate (e.g., phototropic response, avoidance response, and geotropic response). Prior research demonstrates that wall mechanical properties are altered to regulate elongation growth rate during growth responses (Ortega et al., 1975, 1988, 1989; Ortega and Gamow, 1976, 1977), and both turgor pressure and wall mechanical properties are altered to regulate elongation growth rate during development (Ortega et al., 1991).
It was shown that the in vivo mechanical extensibility of the wall increases during light and avoidance growth responses (Ortega et al., 1975; Ortega and Gamow, 1976, 1977). However, it could not be determined whether the magnitude of the change in mechanical extensibility could completely account for the measured change in elongation growth rate. The results of those investigations demonstrated the need for a quantitative biophysical model for elongation growth rate in order to understand how it is regulated and to elucidate the relationship between the wall extensibility and turgor pressure during regulation. Subsequently, pressure probe methods were developed to determine the in vivo mechanical behavior of the elongating wall during sensory responses (Ortega et al., 1988) and during different stages of development (Ortega et al., 1989, 1991). In those studies, a modified form of the Augmented Growth Equation (Ortega, 1985; Ortega et al., 1989, 1991) was established to provide a quantitative biophysical model for the elongation growth rate of sporangiophores. Within the Augmented Growth Equation, the magnitude and behavior of inclusive biophysical variables are related to biological processes involved in elongation growth (Ortega, 1985, 2004, 2010). The results demonstrate that the magnitudes of the biophysical variables, mg (longitudinal irreversible wall extensibility of the growth zone) and PC (critical turgor pressure, sometimes called the yield threshold, Y), are changed to regulate the elongation growth rate during growth responses (Ortega et al., 1988) and during development (Ortega et al., 1989, 1991). Both mg and PC are biomechanical variables that determine the magnitude of irreversible deformation rate of the wall. Also, it was found that the turgor pressure, P, changes in magnitude during development (Ortega et al., 1991) but not during the light and avoidance growth responses (Ortega et al., 1988). In addition, it was determined that the magnitude of mg is a function of both the relative longitudinal irreversible wall extensibility in the growth zone, φg, and the length of the growth zone, Lg, although a formal derivation of the relationship was not provided (Ortega et al., 1991).
Prior research that focused on sensory transduction has produced many mutant strains of P. blakesleeanus that exhibit abnormal phototropic responses. These mutant strains are termed mad mutants (Bergman et al., 1969, 1973; Cerda-Olmedo and Lipson, 1987). Bergman et al. (1973) grouped mad mutant strains into three classes based on their geotropic responses, avoidance responses (sometimes called autochemotropic responses), and mycelial responses to light. Because class-two mutant strains are defective in all tropic responses (tropism is produced by differential elongation rate on opposite sides of the growth zone), Bergman et al. (1973) suggested that the mutation was in the output (i.e., growth regulation), but this was not experimentally verified. Class-two mutants are termed “stiff” mutants because of their diminished or non-existent tropic responses. Ootaki et al. (1974) conducted genetic complementation tests on mutant strains from each of the three classes and identified two genes associated with the tested class-two mutant strains, madD and madE. Subsequent research (Ootaki et al., 1977; Ootaki and Miyazaki, 1993) identified additional genes associated with class-two mutants, some of which are used to obtain insight into the mechanisms and interactions of the sensory transduction pathways (Campuzano et al., 1996; Grolig et al., 2000). Thus for the strains tested, stiff mutant strains are defective in genes madD, E, F, G, and J (Campuzano et al., 1996; Grolig et al., 2000).
In the present study, it is hypothesized that the magnitudes of the biophysical variables that regulate elongation rate are different for stiff mutant strains compared to those of wild type (WT). The biophysical variables, mg, P, and PC, for stage IVb sporangiophores from stiff mutant strains are determined and compared to respective variables previously obtained from WT stage IVb sporangiophores (Ortega et al., 1989). Two strains of stiff mutants, C149 madD120 (−) and C216 geo- (−), are studied. It is found that the magnitude of mg is much smaller for the sporangiophores from these stiff mutant strains compared to the WT. This finding appears to present a paradox because the elongation growth rates of stiff mutants and WT sporangiophores are statistically the same magnitude. However, after determining the magnitudes of P and PC, it is discovered that the magnitudes of P and the difference (P – PC) are significantly larger for stiff mutant sporangiophores and compensate for the smaller magnitude of mg. Other experimental results demonstrate that the smaller magnitude of mg occurs because of a decrease in the magnitudes of both the length of the growth zone, Lg, and relative longitudinal irreversible wall extensibility in the growth zone, φg. A decrease in either Lg or φg can account for the diminished tropic responses of the stiff mutant sporangiophores.
Previously, it was concluded that a quantitative biophysical model for elongation growth rate of the sporangiophore was needed in order to understand how it is regulated. Therefore in this study, a modified Augmented Growth Equation is formally derived for cells in which expansive growth occurs in a localized region of the cell wall, i.e., in a “growth zone.” Expansive growth in a growth zone is common in fungal sporangiophores (Bergman et al., 1969; Cerda-Olmedo and Lipson, 1987), fungal hyphae (Heath, 1990), root hairs (Dumais et al., 2004), and pollen tubes (Fayant et al., 2010) of plants. Importantly, the derivation of the modified Augmented Growth Equation explicitly produces a relationship between mg, φg, and Lg, and in addition, accounts for the elastic elongation within the growth zone and within the non-growing wall of the stalk adjacent to the growth zone. Also, the derivation recovers previous forms of the modified Augmented Growth Equation that have been used to interpret and analyze the results of prior investigations.
Materials and Methods
Biological Material
Vegetative spores of the WT strain of Phycomyces blakesleeanus NRRL1555 (−) were originally obtained from Biology Division, California Institute of Technology, Pasadena, USA. Stiff mutant strains C216 geo- (−) and C149 madD120(−) were obtained from Ishinomaki Senshu University, Miyagi, Japan. The WT sporangiophores are inoculated on sterile growth medium consisting of 4% (w/v) potato dextrose agar, 0.1% (v/v) commercial pure vegetable (Crisco soybean) oil and 0.006% (w/v) thiamine as previous described in Ortega et al. (1989, 1991). Sterile growth medium for the mutant strains included the ingredients used for the WT strain plus tryptone pancreatic and granulated yeast extract. After inoculation the vials are incubated under continuous light from four fluorescent lamps (cool-white, 40 W each; located 0.5 m above the vials) at high humidity and constant temperature (21 ± 1°C) as previously described by (Ortega et al., 1989, 1991). Typically, sporangiophores appeared by the end of the third day. The sporangiophores are plucked daily so that a new crop is available the following day. Stage IVb sporangiophores, 2–3 cm in length, are selected for experiments from the third to seventh crop.
Elongation Growth Rate
The elongation growth rate is determined by measuring the change in length of the sporangiophore, ΔL, at 1-min time intervals and calculating, ΔL/Δt. The length is measured using a long focal length horizontal microscope (Gaertner; 7011K eyepiece and 32 m/m EFL objective) mounted to a 3-D micromanipulator (Line Tool Co.; model H-2, with digital micrometer heads). An electronic timer is used to measure the time intervals.
Growing Zone Length
The length of the growing zone is measured by putting small corn starch grains as markers (10–60 μm in diameter) at three different locations on the stalk of stage IVb sporangiophore and measuring their location on the sporangiophore at regular time intervals (usually 3 min). The individual marker location is measured using a long focal length horizontal microscope mounted to a 3-D micromanipulator. An electronic timer is used to measure time intervals. Marker 1 is the base of the sporangium, marker 2 is approximately 500 μm from the base, and marker 3 is approximately 1000 μm from the base. Their displacement from their initial location is plotted as a function of time. The end of the growth zone is determined to be at a location where the longitudinal displacement of a marker is approximately zero. Starch grain markers that showed little or no displacement in time (typically less than 20 μm displacement in a 10 to 20 min interval) were considered to be in the non-growing region of the stalk.
Turgor Pressure
The turgor pressure of the sporangiophore is measured continuously with a manual version of the pressure probe (Ortega et al., 1989, 1991). A gage pressure transducer is used in the pressure probe, which measured the difference between the absolute pressure and the local atmospheric pressure; the gage pressure transducer was purchased from Kulite Semiconductor Products, Ridgefield, NJ, USA (model XT-190-300G) and calibrated inside the pressure probe with a Heise Bourdon Tube Pressure Gauge (Dresser Industries, Newton, CT, USA; model CMM, 0-200 PSIG Range). The transducer’s output is recorded on a Houston Omniscribe Stripchart Recorder (Ametek; model D5217-2).
The pressure probe was mounted on a 3-D micromanipulator so that its microcapillary tip (typically 5–10 μm outer diameter) could be guided to impale the sporangiophore under visual observation using a horizontally mounted EZM-2TR Trinocular Zoom Stereomicroscope (Meiji Labax Co., Tokyo, Japan). The microcapillary of the pressure probe was filled with inert silicone oil (Dow Corning Corp.; fluid 200, 1–2 centistoke viscosity). After the cell was impaled, the cell sap-oil interface was maintained at a fixed location within the microcapillary tip to measure the turgor pressure of the sporangiophore (Ortega et al., 1989, 1991). A small step-up in turgor pressure was produced by continuously injecting inert silicone oil into the vacuole of the impaled cell to maintain the higher pressure. Typically, after a period of time, the amount of injected oil decreases until no additional injections are required to maintain the turgor pressure at the higher value.
In vivo Creep Experiments
The in vivo creep experiment requires that an instantaneous increase in turgor pressure (turgor pressure step-up) is produced in the sporangiophore and that the elongation growth rate is measured before and after the turgor pressure step-up (Ortega et al., 1989, 1991). The biophysical variables, mg and PC, can be determined with the previously established method which employ Eqs 1 and 2 (Ortega et al., 1989, 1991).
The biophysical variable, mg, is determined by measuring the difference in elongation growth rate, ΔdL/dt, before and after the turgor pressure step-up, and dividing by the magnitude of the turgor pressure step-up, ΔP (Ortega et al., 1989, 1991). This is the same method previously used by Green et al. (1971) and Okamoto et al. (1989) to determine the irreversible wall extensibility of Nitella and Vigna unguiculata, respectively. Once mg is determined, PC may be determined by using Eq. 2 (Ortega et al., 1989, 1991) and the data before the turgor pressure step-up (since mg, dL/dt, and P are known and constant during the period of growth before the step change in P):
This method is the same as that previously used to determine PC for WT stage I and stage IVb sporangiophores (Ortega et al., 1989, 1991).
Protocol for in vivo Creep Experiments
A stage IVb sporangiophore (typically 2–3 cm in length) in a glass shell vial is selected and adapted for 30–45 min to the room temperature of 21–22°C (Figure 2), to room lights (cool-white fluorescent lamps hung from the ceiling), and to bilateral swan-neck light guides (from Schoelly Fiberoptic; the end of each light guide is positioned approximately 8–12 cm on either side of the sporangiophore at an angle of about 30° from the horizontal) from a fiberoptic illuminator (Flexilux 90; HLU Light Source 90/W from Schoelly Fiberoptic, Denzlingen, FRG, which filtered out nearly all of the infrared light). Following this adaptation period, elongation measurements are initiated and continued at 1-min intervals for the remainder of the experiment. After a 10–20 min period of steady elongation growth rate is observed, the sporangiophore is impaled by the microcapillary tip of the pressure probe to measure the turgor pressure. Afterward, the turgor pressure and growth rate are simultaneously measured and monitored for another 5–10 min period to ensure that they are constant. Following this monitoring period, a small turgor pressure step-up (0.01–0.02 MPa) is produced in the sporangiophore by injecting inert silicone oil into the cell vacuole with the pressure probe. In general, the turgor pressure and the elongation growth rate are measured for another 20–50 min. In theory, a turgor pressure step-down can be used for an in vivo creep experiment. In practice a turgor pressure step-down can be produced by removing cell sap with the pressure probe. However, the cell sap of the sporangiophore is very sticky, and in a short period of time (1–10 min) the cell sap will plug the microcapillary tip and once the microcapillary tip is plugged the turgor pressure can no longer be measured (Ortega et al., 1989, 1991). Therefore all our experiments use only a step-up in turgor pressure for the in vivo creep experiments.
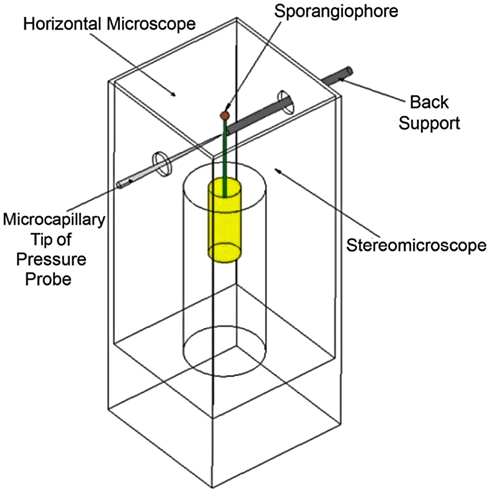
Figure 2. Experimental apparatus for pressure probe experiments. A stage IVb sporangiophore is inserted into a holder within the chamber where it is adapted (see “Protocol for in vivo creep experiments” in the Materials and Methods for details). A back support (metal rod) supports the sporangiophore stalk while the microcapillary tip of the pressure probe impales the stalk below the growth zone. A stereomicroscope is used to observe cell sap-oil interface and a horizontal microscope is used to measure the elongation as a function of time.
Results
Theory
Previous investigations (Ortega et al., 1975; Ortega and Gamow, 1976, 1977) demonstrate the need for a quantitative biophysical model for elongation growth rate in order to understand how elongation growth is regulated and to elucidate the relationship between the wall extensibility and turgor pressure during growth regulation. A biophysical equation describing the elongation rate for fungal and plant cells with a “growth zone” can be derived from the Augmented Growth Equation (Cosgrove, 1985; Ortega, 1985). The Augmented Growth Equation, Eq. 3, describes the relative rate of change in volume of the cell wall chamber, (dV/dt)/V, as the sum of irreversible deformation rate and reversible (elastic) deformation rate of the wall. The Augmented Growth Equation is derived from Lockhart’s Equation (Lockhart, 1965) by augmenting it with a term that accounts for elastic deformation of the expanding wall. Equation 3 is written in relative terms (Ortega, 1985).
The volume of the cell wall chamber is V, t is the time, φ is the relative irreversible wall extensibility, P is the turgor pressure, PC is the critical turgor pressure (sometimes referred to as the yield threshold, Y), and ε is the volumetric elastic modulus of the wall. Implicit within this equation is that both irreversible wall deformation and elastic wall deformation occur over the entire cell wall chamber. Therefore, Eq. 3 is applicable for “diffuse” growth, where the expansion of the cell wall occurs over the entire cell surface and which is the case for most plant cells in tissue and most algal cells.
For a cylindrical cell that enlarges predominately in length and throughout its length, then V = Ac L, where Ac is the cross-sectional area and L is the length. Now if dL/dt >> dAc/dt, then Ac may be assumed to be constant as a first approximation and Eq. 4 is obtained.
The biophysical variable φ L is the relative longitudinal irreversible wall extensibility and ε L is the longitudinal component of the volumetric elastic modulus (longitudinal volumetric elastic modulus). If the change in length of the cylindrical cell that occurs during an experiment is small compared to the overall length, then (dL/dt)/L ≅ (dL/dt)/Lo, where Lo is the length of the cell at the beginning or end of the experiment. Often it is convenient to use this approximation in Eq. 4 and multiply by Lo to obtain Eq. 5.
The biophysical variable mL is the longitudinal irreversible wall extensibility and is equal to the product of the relative longitudinal irreversible wall extensibility and the initial (or final) length of the cell, i.e., mL = φL Lo. Equation 5 is used to interpret and analyze the results of pressure probe experiments conducted on the algal internode cells of Chara corallina (Proseus et al., 1999, 2000) in which elongation growth occurs throughout the length of the cell. Good agreement was demonstrated between Eq. 5 and the measured elongation growth before, during, and after steps-up and steps-down in turgor pressure for C. corallina (Proseus et al., 1999, 2000).
Conceptually, it is useful to visualize a dashpot element and spring element in series to represent the mechanical properties of the growing cell wall (Figure 3A) for cells that undergo diffuse growth, i.e., most plant and algal cells. The dashpot element (similar to a shock absorber) deforms irreversibly to an applied force (or stress) and represents the irreversible wall deformation behavior during expansive growth. Furthermore, the dashpot is filled with a Bingham fluid, which behaves like a Newtonian fluid (a linear relationship between deformation rate and force) after the force (or stress) exceeds some magnitude, or P exceeds PC. The spring element represents the reversible (elastic) deformation behavior that occurs after a force or stress is applied, and represents the reversible deformation of the wall when the turgor pressure is larger than zero. It is noted that elastic deformation of the wall (growing or non-growing) will increase and decrease as the turgor pressure increases and decreases. Also, the relationship between the elastic deformation and the turgor pressure is not always linear. Equations 3, 4, and 5 are mathematical representations of the dashpot and spring in series, see Figure 3A.
Figure 3. Schematic illustrations of the wall mechanical properties for cells exhibiting “diffuse growth” (A) and “tip growth” (B). The growth zone is light green and non-growing wall is dark green. For diffuse growth (A), elongation growth occurs over the entire wall that exhibits both irreversible deformation (Bingham dashpot) and elastic deformation (spring). For tip growth (B), elongation growth only occurs within the growth zone that exhibits both irreversible deformation (Bingham dashpot) and elastic deformation (spring); the non-growing stalk only exhibits elastic deformation (spring).
Importantly, Figure 3A and the mathematical representations (Eqs 3, 4, and 5) are not applicable for cells with a distinct growth zone, within which the wall deforms both irreversibly and elastically, and which is adjacent to a non-growing portion of the wall that only deforms elastically. Cells that exhibit tip growth (root hairs, pollen tubes, and fungal hyphae), apical growth (stage I sporangiophores), and intercalary growth (stage IV sporangiophores) require a different model to describe elongation rate. Conceptually, the cell wall with a distinct growth zone can be accurately modeled by a dashpot element and spring element in series for the growing wall within the growth zone and that is in series with another spring element, which represents the mechanical behavior of the non-growing wall (Figure 3B). It is noted, that the elastic properties (springs) within the growing wall and non-growing wall are different.
In the case where the cylindrical cell only elongates within a growth zone which is shorter than the length of the cell and remains approximately constant in length, (as is the case for fungal hyphae, root hairs, pollen tubes, and sporangiophores of P. blakesleeanus, stage I and stage IVb), then the relative rate of change in length that occurs in the growth zone is [(dL/dt)/L]g = [dL/dt]g/Lg, where Lg is the length of the growth zone and essentially constant. Substituting this term into Eq. 4 and multiplied by Lg, Eqs 6 and 7 are obtained for the elongation rate that occurs within the growth zone; [dL/dt]g.
or
The biophysical variable mg is the longitudinal irreversible wall extensibility of the growth zone and is equal to the product of the relative longitudinal irreversible wall extensibility within the growth zone, φg, and the length of the growth zone, Lg, i.e., mg = φg Lg. The biophysical variable ε Lg is the longitudinal volumetric elastic modulus within the growth zone.
Now the relative change in length that occurs in the non-growing wall of a cylindrical cell (non-growing stalk) is [(dL/dt)/L]s = [dL/dt]s/Ls, where Ls is the length of the non-growing stalk. If the change in length of the stalk that occurs during an experiment is small compared to the overall length (as is the case for most experiments with the sporangiophores of P. blakesleeanus), then Ls may be assumed to be constant as a first approximation. Experimental results demonstrate that only elastic deformation occurs within the non-growing stalk (Ahlquist and Gamow, 1973). Considering only elastic extension, Eq. 8 is obtained.
The longitudinal volumetric elastic modulus within the non-growing stalk is ε Ls. Multiplying Eq. 8 by Ls, Eq. 9 is obtained.
Now the total elongation rate, dL/dt, is the sum of the elongation rates within the growth zone and within the stalk, i.e., dL/dt = [dL/dt]g + [dL/dt]s. Substituting in the relevant expressions for Eqs 7 and 9, then Eqs 10 and 11 are obtained.
(elongation rate) = (irreversible rate in growth zone) + (elastic rate in growth zone) + (elastic rate in stalk)
(elongation rate) = (irreversible rate in growth zone) + (elastic rate in growth zone and stalk)
Note that the elastic elongation (deformation) rate of the wall only occurs when the turgor pressure changes (dP/dt ≠ 0) and its magnitude depend on biophysical variables, ε Lg and ε Ls (Figure 3B). When the P is constant, i.e., dP/dt = 0, then Eqs 10 and 11 become Eq. 12.
(elongation rate) = (irreversible rate of growth zone)
Equation 12 is used to interpret and analyze the results of experiments conducted on stage I (Ortega et al., 1991) and stage IVb sporangiophores (Ortega et al., 1989) of WT P. blakesleeanus, and on stiff mutant stage IVb sporangiophores in this study. Importantly, a relationship between mg, φg, and Lg (mg = φg Lg) is explicitly obtained in the derivation (Eqs 6 and 7).
Experimental Results
The magnitudes of the biophysical variables dL/dt, mg, P, and PC are determined from in vivo creep experiments conducted on stage IVb sporangiophores from stiff mutant strains, C216 geo- (−) and C149 madD120 (−), using the method previously established by Ortega et al. (1989, 1991). The pressure steps-up used in the experiments are of similar magnitudes to those previously used (Ortega et al., 1989, 1991), i.e., between 0.014 and 0.017 MPa, however the magnitude of the response (change in slope of L vs. t curve) are smaller (Figure 4) than those obtained with WT (Ortega et al., 1989, 1991). The growth zone lengths, Lg, are determined in separate experiments and the magnitude of φg is calculated using mean values of mg and Lg; φg = mg Lg−1. Table 1 presents the measured and determined values for dL/dt, mg, P, PC, (P – PC), Lg, and φg for WT (Ortega et al., 1989, 1991), and stiff mutant (C216 and C149) stage IVb sporangiophores. The results demonstrate that the elongation growth rates (dL/dt) of WT, C216, and C149 stage IVb sporangiophores are essentially the same magnitude; statistical results of t-tests indicate that there are no significant differences. In contrast, the magnitudes of mg, PC, and Lg are smaller while the magnitudes of P and (P – PC) are larger for stage IVb sporangiophores from C216 and C149 strains compared to those of WT. Statistical results of t-tests indicate that the magnitudes of mg, P, PC, (P – PC), and Lg obtained from stage IVb sporangiophores of C216 and C149 strains are significantly different from the respective magnitudes obtained from WT.
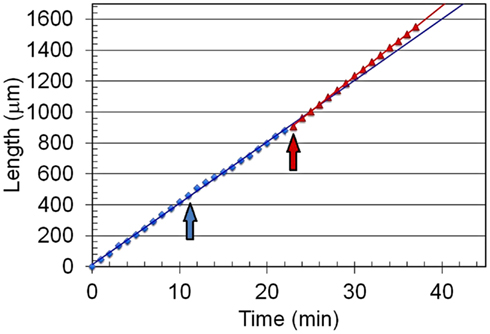
Figure 4. Elongation as a function of time for an in vivo creep experiment. The length is plotted against time for a stiff mutant stage IVb sporangiophore (C216). The first vertical arrow (blue) indicates the time when the stalk of the sporangiophore was impaled to measure the turgor pressure. The second arrow (red) indicates the time when the step-up in turgor pressure was produced with the pressure probe by continually injecting oil into the vacuole to maintain the higher pressure. The data points before (blue) and after (red) the turgor pressure step-up are each fit with a straight line. It can be seen that the slope of the red line (after the turgor pressure step-up) is larger than that of the blue line (before the turgor pressure step-up).
Values for dL/dt, mg, and (P – PC) are normalized and presented in Figure 5. Normalized values for each variable are obtained by dividing the average values presented in Table 1 for WT and stiff mutant (C216 and C149) sporangiophores by the largest magnitude of the respective variable, e.g., average values of mg presented in Table 1 are divided by 997 μm min−1 MPa−1 in order to obtain the normalized values of mg presented in Figure 5. Values for mg, Lg, and φg are normalized using the same method and presented in Figure 6. The normalized values are used to facilitate an understanding of how the biophysical variables change in stiff mutant sporangiophores.
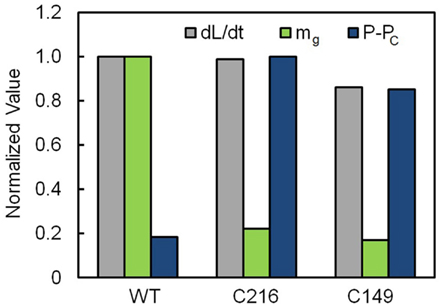
Figure 5. Normalized values of dL/dt, mg, and (P – PC) for wild type and stiff mutant (C216 and C149) stage IVb sporangiophores. Normalized values for each variable are obtained by dividing the average values presented in Table 1 for wild type (WT) and stiff mutant (C216 and C149) stage IVb sporangiophores by the largest magnitude of the respective variable. The elongation rate, dL/dt (gray bars), of WT and the stiff mutants stage IVb sporangiophores (C214 and C149) are statistically the same magnitude. Stiff mutant stage IVb sporangiophores have significantly smaller magnitudes for mg (green bars) and significantly higher magnitudes of P – PC (blue bars) compared to the WT. The higher magnitudes of P – PC compensate the smaller magnitudes of mg to achieve similar elongation rates exhibited by WT sporangiophores.
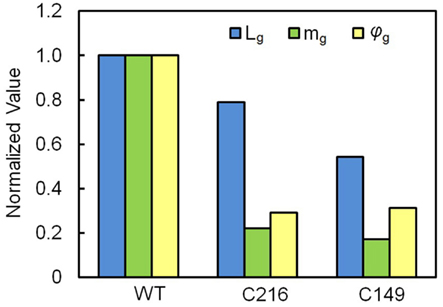
Figure 6. Normalized values of Lg, mg, and φg for wild type (WT) and stiff mutant strain (C216 and C149) stage IVb sporangiophores. Normalized values for each variable are obtained by dividing the average values presented in Table 1 for WT and stiff mutant (C216 and C149) stage IVb sporangiophores by the largest magnitude of the respective variable. The magnitudes of Lg (blue bar), mg (green bar), and φg (yellow bar) for stiff mutant sporangiophores (C216 and C149) are smaller compare to respective magnitudes for WT.
Discussion
Prior experimental research measured the in vivo mechanical extensibility of the stage IVb sporangiophore’s wall before and during the light and avoidance growth responses (Ortega et al., 1975; Ortega and Gamow, 1976, 1977). The results of those investigations demonstrated the need for a quantitative biophysical model for elongation growth rate in order to investigate its regulation because it could not be determined whether the measured change in mechanical extensibility could completely account for the measured change in elongation growth rate. Biophysical equations describing the elongation growth rate of stage IVb sporangiophores (Eqs 10–12) are derived from the Augmented Growth Equation for wall deformation (Ortega, 1985). The derivation recovers previous biophysical equations used to analyze the results of pressure probe experiments conducted on internode cells of C. corallina, Eq. 5 (Proseus et al., 1999, 2000) and sporangiophores of P. blakesleeanus, Eq. 12 (Ortega et al., 1989, 1991). Equations 10 and 11 describe the elongation growth rate when the turgor pressure is changing. Equation 12 describes the elongation growth rate when the turgor pressure is constant. These equations (Eqs 10–12) are appropriate for cells with a distinct growth zone, e.g., stage I and stage IV sporangiophores, fungal hyphae, pollen tubes, and root hairs (Figure 3B). It is noted that Eqs 3–5 are appropriate for cells without a distinct growth zone, e.g., plant cells in tissue and internode cells of algae (Figure 3A).
An important feature of this derivation is the demonstration that φ (relative irreversible wall extensibility) within Eq. 3 is not the appropriate biophysical variable needed to describe the irreversible properties of the wall in cells with a distinct growth zone, because these cells can regulate the overall irreversible extensibility by changing the length of the growth zone, Lg, as well as the magnitude of wall’s ability to extend irreversible, φg. A more appropriate biophysical variable for cells with a distinct growth zone is mg, which is the product of Lg and φg, i.e., mg = φg Lg. Importantly, mg can be determined directly with pressure probe experiments (Ortega et al., 1989, 1991).
The results presented in Table 1 demonstrate that the magnitudes of mg, PC, and Lg decrease while the magnitudes of P and (P – PC) increase for stage IVb sporangiophores from C216 and C149 strains (stiff mutants) compared to those of WT. The finding that magnitudes of both mg and PC decrease for the stiff mutants appears unusual. Previous research that compares the magnitudes of mg and PC for stage I and stage IVb sporangiophores indicates that PC decreases when mg increases (Ortega et al., 1991), which is consistent with the expected behavior of a simple viscoelastic material. The finding that mg and PC both decrease for the stiff mutants suggests that the composition of the growing cell wall and the molecular mechanisms (chemistry) that regulate the magnitudes of mg and PC are more complex than that of a simple viscoelastic material. The finding that mg and PC of the internode cells of C. corallina are both smaller in magnitude compared to respective values for stage I sporangiophores (Ortega, 2004) supports this suggestion, because the composition and chemistry that regulate the magnitudes of mg and PC of the algal walls are different compared to those of the fungal walls.
Interestingly, the elongation rate (dL/dt) for C216, C149, and WT stage IVb sporangiophores are statistically the same magnitude (Table 1). It can be seen with the use of Eq. 12 and the data in Table 1 that decreases in magnitudes of mg for the stiff mutant sporangiophores are compensated by increases in magnitudes of (P – PC) to maintain elongation growth rates, dL/dt, that are of similar magnitude measured for WT sporangiophores.
Normalized values can be used to understand the relationship between relevant biophysical variables. The normalized values for dL/dt, mg, and (P – PC) presented in Figure 5 demonstrate that magnitudes of mg and (P – PC) of stage IVb sporangiophores from C216 and C149 strains decrease and increase, respectively, to maintain elongation growth rates that are of similar magnitudes as those obtained from WT. The decreases in magnitudes of mg indicate a diminished capability of the wall to deform irreversibility in the longitudinal direction. The increases in magnitudes of (P – PC) indicate an increase in the magnitude of effective stress within the wall that produces irreversible deformation. Thus for the two stiff mutant strains studied, the irreversible extension of the wall is significantly reduced and should significantly reduce the elongation rate. However, magnitudes of P and (P – PC) increase, which increases wall stresses that produces irreversible extension for the two stiff mutant strains, and produce elongation growth rates of similar magnitudes measured for WT sporangiophores.
The normalized magnitudes for mg, Lg, and φg presented in Figure 6 demonstrate that decreases in magnitudes of mg for stage IVb sporangiophores from C216 and C149 strains are produced by decreasing both Lg and φg. Decreases in either Lg or φg can diminish the sporangiophore’s ability to produce significant differential elongation rates on opposite sides of the growth zone and thus reduces its ability to undergo tropism. The large decreases in magnitudes of φg, together with significant decreases in Lg, can explain why stage IVb sporangiophores from the two stiff mutant strains (C216 and C149) exhibit almost no tropic response.
The affect of a shorter growth zone on the bending rate is easily visualized. If the sporangiophore is capable of producing a constant bend rate per unit length of growth zone, then it follows that a longer growth zone will produce a larger bend rate compared to a shorter growth zone (Figure 7). This can explain how the shorter growth zones of the stiff mutant strains produce a smaller bend rate compared to WT.
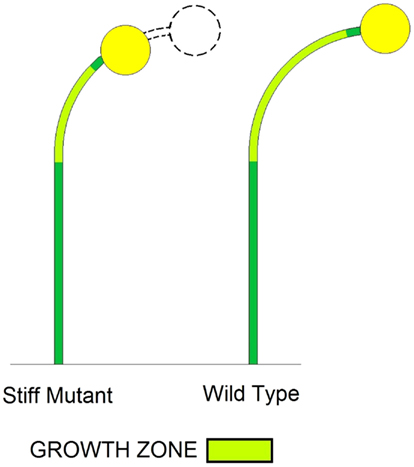
Figure 7. Schematic illustrations showing the affect of a shorter growth zone of a stiff mutant stage IVb sporangiophore on bending angle and bend rate compared to a wild type stage IVb sporangiophore. The stiff mutant stage IVb sporangiophore has a shorter growth zone (light green) compared to the wild type stage IVb sporangiophore. It is assumed that both sporangiophores bend at the same rate, i.e., both growth zones have the same curvature. It can be seen that the longer growth zone of the wild type produces a larger bend angle compared to the stiff mutant with a shorter growth zone. So if the sporangiophore is capable of producing a constant bend rate per unit length of growth zone (same curvature), then it follows that a longer growth zone will produce a larger bend rate compared to a shorter growth zone. This can explain how the shorter growth zones of the stiff mutant stage IVb sporangiophores produce a smaller bend rate compared to wild type.
The affect of a smaller irreversible wall extensibility of the growth zone (φg) is more difficult to visualize, but an example may help to explain how tropism may be reduced for stiff mutant sporangiophores. A WT stage IVb sporangiophore bends toward unilateral light at a rate of 1.5–3.0° min−1 (Cerda-Olmedo and Lipson, 1987). If the average diameter of the sporangiophore’s growth zone is 120 μm, the distal side elongation rate of the growth zone must be approximately 6.0 μm min−1 larger than the proximal side elongation rate to produce a bend rate of 3.0° min−1. Using approximate values from Table 1, it can be determined using Eq. 12 that the proximal side elongation rate (dL/dt)wp is 50 μm min−1 when mg is 1000 μm min−1 MPa−1 and (P – PC) is 0.05 MPa. Using a value for Lg of 2000 μm, then φg is calculated to be 0.5 min−1 MPa−1. If φg is increased by 12% on the distal side then mg is also increased by 12% (φg = 0.56 min−1 MPa−1 and mg = 1120 μm min−1 MPa−1), and the distal side elongation rate (dL/dt)wd = mg (P – PC) = (1120 μm min−1 MPa−1)·(0.05 MPa) = 56 μm min−1. The difference between the distal and proximal elongation rate is (dL/dt)d – (dL/dt)p = 6.0 μm min−1, producing a bend rate of 3.0° min−1.
Now for a stiff mutant sporangiophore, the proximal side elongation rate (dL/dt)sp is 50 μm min−1 when mg is 200 μm min−1 MPa−1 and (P – PC) is 0.25 MPa. Using an average Lg of 1400 μm, then φg is calculated to be 0.143 min−1 MPa−1. Values used for φg, mg, and (P – PC) are approximate average values for C216 and C149 mutant strains (Table 1). Because φg is approximately 3.5 times smaller for the stiff mutants compared to WT, it may be assumed that the increase in φg on the distal side is also 3.5 times smaller. So if φg and mg are increased by 3.4% on the distal side ((φg ≅ 0.149 min−1 MPa−1 and mg ≅ 207 μm min−1 MPa−1), then the distal side elongation rate (dL/dt)sd = mg (P – PC) = (207 μm min−1 MPa−1) (0.25 MPa) = 51.75 μm min−1. The difference between the distal and proximal elongation rate is (dL/dt)sd – (dL/dt)sp = 1.75 μm min−1, producing a bend rate of approximately 0.8° min−1 which is significantly smaller than the bend rate of 3.0° min−1 for the WT sporangiophore.
The difference in the mechanical properties of the cell wall for the WT sporangiophore and the stiff mutant sporangiophore can be illustrated with a dashpot element in series with two spring elements (Figure 8). The cell wall illustrations are similar to that in Figure 3B for a wall that exhibits tip growth. In Figure 8, the growth zone length and the irreversible wall extensibility (Bingham dashpot) are larger for WT sporangiophores’ cell walls (Figure 8A) compared to stiff mutant sporangiophores’ cell walls (Figure 8B). Also, the cell walls of the stiff mutant sporangiophores are under more tension than the WT as illustrated by the larger force arrows at the ends and the more extended springs in their wall (Figure 8B).
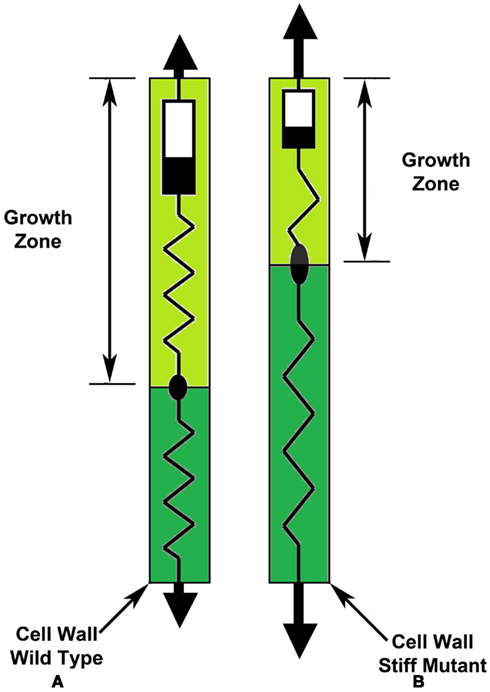
Figure 8. Schematic illustrations of the wall mechanical properties exhibiting tip growth for wild type (A) and stiff mutant sporangiophores (B). Both the growth zone length and the irreversible extensibility (Bingham dashpot) are larger for wall from wild type sporangiophores (A) compared to walls from stiff mutant sporangiophores (B). Also, the cell walls of the stiff mutant sporangiophores (B) are under more tension than the wild type (A) as illustrated by the larger force arrows at the ends and by the more extended springs in their wall.
Additional insight into the biological processes affected in class-two mutant strains (stiff mutants) may be obtained. Prior research show that small vesicles within the cytoplasm move to areas of the wall where expansive growth occurs within cells with a growth zone, e.g., sporangiophores of P. blakesleeanus (Cerda-Olmedo and Lipson, 1987), fungal hyphae (Heath, 1990; Bartnicki-Garcia et al., 2000; Gierz and Bartnicki-Garcia, 2001), and pollen tubes and root hairs (Heath, 1990). It is thought that the small vesicles contain wall-building molecules that are released to the inner cell wall, via exocytosis, and mediate wall loosening and irreversible wall extension of the stressed wall (due to turgor pressure). Research conducted in this study demonstrates that magnitude of elongation growth rate depends on (a) the wall’s ability to extend irreversibly (i.e., the magnitude of φg), (b) the area of wall that extends irreversibly (i.e., the magnitude of Lg), and (c) the magnitude of the effective stress within the wall (i.e., the magnitude of P – PC).
The changes in wall structure and/or architecture that produce the measured mechanical properties and elongation growth behavior of stiff mutant sporangiophores cell wall are unknown, but an examination of a few explanations may be insightful. It may be that the stiff mutant sporangiophores simply deliver more material to the wall making it thicker. Then the thicker wall would exhibit less irreversible extensibility (φg) as demonstrated in this study. However, it would be expected that the delivery of more material to the wall would also extend the length of the growth zone, which is inconsistent with the experimental results demonstrating that Lg of stiff mutant sporangiophores are actually shorter compared to WT. Another idea is that the delivered material makes more bonds with the existing wall material thus tightening and stiffening the wall more to make it less extensible. This idea suggests that the magnitude of φg is reduced for stiff mutants, but the growth zone length is not affected, which is inconsistent with the experimental results that demonstrate a decrease in Lg.
Still another idea is that a smaller amount of wall material is delivered to the inner wall of stiff mutant sporangiophores by transport vesicles and exocytosis. It is hypothesized that the new wall material catalyzes wall loosening in order to incorporate new material into the wall, using a process similar to that proposed for internode cells of C. corallina and plant cells (Boyer, 2009), and that mg is a quantitative measure of the amount of wall loosening. So if the mass flow rate of wall-building molecules delivered to the inner cell wall is reduced, it follows that the magnitudes of mg, φg, and Lg are reduced. Because the measured magnitudes of mg, φg and Lg are significantly smaller for the stiff mutant sporangiophores tested, it can be deduced that the mass flow rates of wall-building molecules delivered to the inner cell wall are significantly smaller. Perhaps exocytosis is affected and/or the number of vesicles carrying wall-building molecules to the wall is smaller for stiff mutant sporangiophores from C216 and C149 strains. In conclusion it would appear that the last explanation is the most consistent with the experimental results. Therefore, it is hypothesized that the defective genes in stiff mutant sporangiophores (madD, E, F, G, and J) reduce the mass flow rate of wall-building materials (that catalyze wall loosening) to the inner wall thus reducing the magnitudes of mg, φg, and Lg, and reducing their ability to perform tropic responses.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Professor Atusushi Miyazaki from Ishinomaki Senshu University for kindly providing spores of C216 and C149 strains. This research was supported by National Science Foundation Grant MCB-0948921 to Joseph K. E. Ortega.
References
Ahlquist, C. N., and Gamow, R. I. (1973). Phycomyces mechanical behavior of stage II and stage IV. Plant Physiol. 51, 586–587.
Bartnicki-Garcia, S., Bracker, C. E., Glerz, G., Lopez-Franco, R., and Lu, H. (2000). Mapping the growth of fungal hyphae orthogonal cell wall expansion during tip growth and the role of turgor. Biophys. J. 79, 2382–2390.
Baskin, T. I. (2005). Anisotropic expansion of the plant cell wall. Annu. Rev. Cell Dev. Biol. 21, 203–222.
Bergman, K., Burke, P. V., Cerda-Olmedo, E., David, C. N., Delbruck, M., Foster, K. W., Goodell, E. W., Heinsenberg, M., Meissner, G., Zalokar, M., Dennison, D. S., and Shropshire, W. Jr. (1969). Phycomyces. Bacteriol. Rev. 33, 99–157.
Bergman, K., Eslava, A. P., and Cerda-Olmedo, E. (1973). Mutants of Phycomyces with abnormal phototropism. Mol. Gen. Genet. 123, 1–16.
Boyer, J. S. (2009). Evans review: cell wall biosynthesis and the molecular mechanism of plant enlargement. Funct. Plant Biol. 36, 383–394.
Campuzano, V., Galland, P., Alvarez, M. I., and Eslava, A. P. (1996). Blue-light receptor requirement for gravitropism, autochemotropism and ethylene response in Phycomyces. Photochem. Photobiol. 63, 686–694.
Castle, E. S. (1942). Spiral growth and the reversal of spiraling in Phycomyces, and their bearing on primary wall structure. Am. J. Bot. 29, 664–672.
Cerda-Olmedo, E., and Lipson, E. D. (1987). Phycomyces. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press.
Cosgrove, D. J. (1985). Cell wall yield properties of growing tissue evaluation by in vivo stress relaxation. Plant Physiol. 78, 347–356.
Dumais, J., Long, S. R., and Shaw, S. L. (2004). The mechanics of surface expansion anisotropy in Medicago truncatula root hairs. Plant Physiol. 136, 3266–3275.
Dumais, J., Shaw, S. L., Steele, C. R., Long, S. R., and Ray, P. M. (2006). An anisotropic-viscoplastic model of plant cell morphogenesis by tip growth. Int. J. Dev. Biol. 50, 209–222.
Fayant, P., Girlanda, O., Chebli, Y., Aubin, C.-E., Villemure, I., and Geitmann, A. (2010). Finite element model of polar growth in pollen tubes. Plant Cell 22, 2579–2593.
Geitmann, A., and Ortega, J. K. E. (2009). Mechanics and modeling of plant cell growth. Trends Plant Sci. 14, 467–478.
Gierz, G., and Bartnicki-Garcia, S. (2001). A three-dimensional model of fungal morphogenesis based on the vesicle supply center concept. J. Theor. Biol. 208, 151–164.
Goriely, A., and Tabor, M. (2008). Mathematical modeling of hyphal tip growth. Fungal Biol. Rev. 22, 77–83.
Goriely, A., and Tabor, M. (2011). Spontaneous rotational inversion in Phycomyces. Phys. Rev. Lett. 106, 138103.1–138103.4.
Green, P. B., Erickson, R. O., and Buggy, J. (1971). Metabolic and physical control of cell elongation rate: in vivo studies in Nitella. Plant Physiol. 47, 423–430.
Grolig, F., Eibel, P., Schimek, C., Schapat, T., Dennison, D. S., and Galland, P. A. (2000). Interaction between gravitropism and phototropism in sporangiophores of Phycomyces blakesleeanus. Plant Physiol. 123, 765–776.
Lockhart, J. A. (1965). An analysis of irreversible plant cell elongation. J. Theor. Biol. 8, 264–275.
Okamoto, H., Liu, Q., and Katoa, K. (1989). Regulation of elongation growth of excised segments of Vigna hypocotyl under osmotic stress in the absence or presence of absorbable solute. Plant Cell Physiol. 30, 1039–1046.
Ootaki, T., Fisher, E. P., and Lockhart, P. (1974). Complementation between mutants of Phycomyces with abnormal phototropism. Mol. Gen. Genet. 131, 233–246.
Ootaki, T., Kinno, T., Yoshida, K., and Eslava, A. P. (1977). Complementation between Phycomyces mutants of mating type (+) with abnormal phototropism. Mol. Gen. Genet. 152, 245–251.
Ootaki, T., and Miyazaki, A. (1993). Genetic Nomenclature and Strain Catalogue of Phycomyces. Sendai: Tohoku University.
Ortega, J. K. E. (1985). Augmented growth equation for cell wall expansion. Plant Physiol. 79, 318–320.
Ortega, J. K. E. (2004). “A quantitative biophysical perspective of expansive growth for cells with walls,” in Recent Research Development in Biophysics, Vol. 3, ed. S. G. Pandalai (Kerala: Transworld Research Network), 297–324.
Ortega, J. K. E., and Gamow, R. I. (1974). The problem of handedness reversal during the spiral growth of Phycomyces. J. Theor. Biol. 47, 317–332.
Ortega, J. K. E., and Gamow, R. I. (1976). An increase in mechanical extensibility during the period of light stimulated growth. Plant Physiol. 57, 456–457.
Ortega, J. K. E., and Gamow, R. I. (1977). Phycomyces: an increase in mechanical extensibility during the avoidance growth response. Plant Physiol. 60, 805–806.
Ortega, J. K. E., Gamow, R. I., and Ahlquist, N. C. (1975). Phycomyces: a change in mechanical properties after light stimulus. Plant Physiol. 55, 333–337.
Ortega, J. K. E., Harris, J. F., and Gamow, R. I. (1974). The analysis of spiral growth in Phycomyces using a novel optical method. Plant Physiol. 53, 485–490.
Ortega, J. K. E., Manica, K. J., and Keanini, R. G. (1988). Phycomyces: turgor pressure behavior during the light and avoidance growth response. Photochem. Photobiol. 48, 697–703.
Ortega, J. K. E., Smith, M. E., Erazo, A. J., Espinosa, M. A., Bell, S. A., and Zehr, E. G. (1991). A comparison of cell-wall-yielding properties for two developmental stages of Phycomyces sporangiophores: determination by in-vivo creep experiments. Planta 183, 613–619.
Ortega, J. K. E., Zehr, E. G., and Keanini, R. G. (1989). In vivo creep and stress relaxation experiments to determine the wall extensibility and yield threshold for the sporangiophores of Phycomyces. Biophys. J. 56, 465–475.
Proseus, T. E., Ortega, J. K. E., and Boyer, J. S. (1999). Separating growth from elastic deformation during cell enlargement. Plant Physiol. 119, 775–784.
Proseus, T. E., Zhu, G. L., and Boyer, J. S. (2000). Turgor, temperature and the growth of plant cells: using Chara corallina as a model system. J. Exp. Bot. 51, 1481–1494.
Richmond, P. A., Métraux, J.-P., and Taiz, L. (1980). Cell expansion patterns and directionality of wall mechanical properties in Nitella. Plant Physiol. 65, 211–217.
Roelofsen, P. A. (1950). The origin of spiral growth in Phycomyces sporangiophores. Rec. Trav. Bot. Neerl. 42, 72–110.
Keywords: Phycomyces, stiff mutants, madD to madJ, tropic responses, growth zone, turgor pressure
Citation: Ortega JKE, Munoz CM, Blakley SE, Truong JT and Ortega EL (2012) Stiff mutant genes of Phycomyces affect turgor pressure and wall mechanical properties to regulate elongation growth rate. Front. Plant Sci. 3:99. doi: 10.3389/fpls.2012.00099
Received: 03 February 2012; Accepted: 27 April 2012;
Published online: 21 May 2012.
Edited by:
Yoel Forterre, Centre Nationale de la Recherche Scientifique, FranceReviewed by:
Yoel Forterre, Centre Nationale de la Recherche Scientifique, FranceAnja Geitmann, Université de Montréal, Canada
Copyright: © 2012 Ortega, Munoz, Blakley, Truong and Ortega. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Joseph K. E. Ortega, Bioengineering Laboratory, Department of Mechanical Engineering, University of Colorado Denver, Campus Box 112, PO Box 173364, Denver, CO 80217-3364, USA. e-mail:am9zZXBoLm9ydGVnYUB1Y2RlbnZlci5lZHU=

 Cindy M. Munoz
Cindy M. Munoz