- Department of Plant and Environmental Sciences, University of Copenhagen, Copenhagen, Denmark
Plasmodesmata (PD) play a key role in loading of sugars into the phloem. In plant species that employ the so-called active symplasmic loading strategy, sucrose that diffuses into their unique intermediary cells (ICs) is converted into sugar oligomers. According to the prevalent hypothesis, the oligomers are too large to pass back through PD on the bundle sheath side, but can pass on into the sieve element to be transported in the phloem. Here, we investigate if the PD at the bundle sheath-IC interface can indeed fulfill the function of blocking transport of sugar oligomers while still enabling efficient diffusion of sucrose. Hindrance factors are derived via theoretical modeling for different PD substructure configurations: sub-nano channels, slit, and hydrogel. The results suggest that a strong discrimination could only be realized when the PD opening is almost as small as the sugar oligomers. In order to find model parameters that match the in vivo situation, we measured the effective diffusion coefficient across the interface in question in Cucurbita pepo with 3D-photoactivation microscopy. Calculations indicate that a PD substructure of several sub-nano channels with a radius around 7 Å, a 10.4 Å-wide slit or a hydrogel with 49% polymer fraction would be compatible with the effective diffusion coefficient. If these configurations can accommodate sufficient flux of sucrose into the IC, while blocking raffinose and stachyose movement was assessed using literature data. While the slit-configuration would efficiently prevent the sugar oligomers from “leaking” from the IC, none of the configurations could enable a diffusion-driven sucrose flux that matches the reported rates at a physiologically relevant concentration potential. The presented data provides a first insight on how the substructure of PD could enable selective transport, but indicates that additional factors are involved in efficient phloem loading in active symplasmic loading species.
Introduction
An essential step for the distribution of carbohydrates throughout the whole plant is the loading of carbohydrates into the phloem in source organs. A number of herbaceous angiosperms, as e.g., the Cucurbits, preferentially transport the sugar oligomers raffinose and stachyose in the phloem, in contrast to the majority of plants where sucrose is transported exclusively (Rennie and Turgeon, 2009; Davidson et al., 2011). They are therefore referred to as raffinose family oligosaccharide (RFO)-transporting plants.
According to our current understanding of phloem transport in these species, the conversion of sucrose into RFOs is of key importance for the loading of sugars into the phloem (Rennie and Turgeon, 2009; Liesche and Schulz, 2013). RFO-transporting plants are also characterized by an abundance of plasmodesmata (PD) at all cell wall interfaces between the sucrose-producing mesophyll cells and the phloem sieve elements. These PD were shown to be functional in experiments using fluorescent tracer molecules indicating that sucrose diffuses freely between the cells (Turgeon and Hepler, 1989; Liesche and Schulz, 2012a). The higher sugar concentration that has been measured in the phloem compared to the rest of the leaf is explained according to the polymer-trap hypothesis by the conversion of sucrose that enters the specialized phloem companion cells, called intermediary cells (IC), into sugar oligomers (Haritatos et al., 1996; McCaskill and Turgeon, 2007). As the sucrose concentration is thereby constantly reduced, it can be replenished by diffusion from mesophyll to phloem along the sucrose concentration gradient. The sugar polymers are deemed too large to pass through PD on the bundle sheath cell (BSC) side, but can pass on into the sieve element to be transported in the phloem.
Circumstantial evidence for this theory is given by the IC-specific expression of sugar-oligomerizing enzymes (Beebe and Turgeon, 1992; Haritatos et al., 2000; Volk et al., 2003) and the abundance of PD with a unique structure at the BSC-IC interface. These PD are highly branched, with more branches on the IC side (Turgeon et al., 1975; Volk et al., 1996). These branches on the IC side are generally described as very narrow, with no cytoplasmic sleeve visible between the plasma membrane and the desmotuble (Fisher, 1986; Turgeon et al., 1993). The only indication that the PD can indeed fulfill a filtering function as anticipated in the polymer-trap hypothesis comes from expression of raffinose biosynthesis genes in tobacco companion cells, which does not result in efficient phloem transport, probably because they lack the structural specialization of IC (Hannah et al., 2006).
It is generally assumed that small molecules (below 1 kD) can freely diffuse from cell to cell through a cytoplasmic sleeve in the PD between plasma membrane and desmotuble (Terry and Robards, 1987; Maule et al., 2011). Only in one case has selective transport of small molecules been shown: small fluorescent tracers could pass from a leaf epidermal cell into the basal cell of trichomes, but not the other way round (Christensen et al., 2009). This phenomenon remains unexplained. Size-dependent filtering by PD is well-established for larger molecules, like proteins, and PD in different tissue were found to have different size-exclusion limit (Kim et al., 2005).
In the present work, we test the validity of the polymer-trap hypothesis by theoretical modeling of diffusion of sucrose, raffinose, and stachyose through PD with different substructural configurations. Potential configurations are predicted by comparing the model data with the experimentally determined diffusion coefficient at the interface in question. The predictions are evaluated using literature data on sugar concentration potentials and flow.
Theory and Results
Hydrodynamic Radii of Sucrose, Raffinose, and Stachyose
The size of the molecules in question is an essential parameter for the following considerations on plasmodesmal filtering. The size of the hydrated molecule is reflected in the hydrodynamic radius. Hydrodynamic radii can be calculated using the Stokes–Einstein equation after determining the diffusion coefficient experimentally (Pappenheimer, 1953; Schultz and Solomon, 1961).
with Boltzman's constant , absolute temperature T (298 K), diffusion coefficient of the sugar D, and viscosity η (0.89 centipoise for water). Values for sucrose, raffinose, and stachyose as well as the symplasmic tracer fluorescein derived in this way are listed in Table 1.
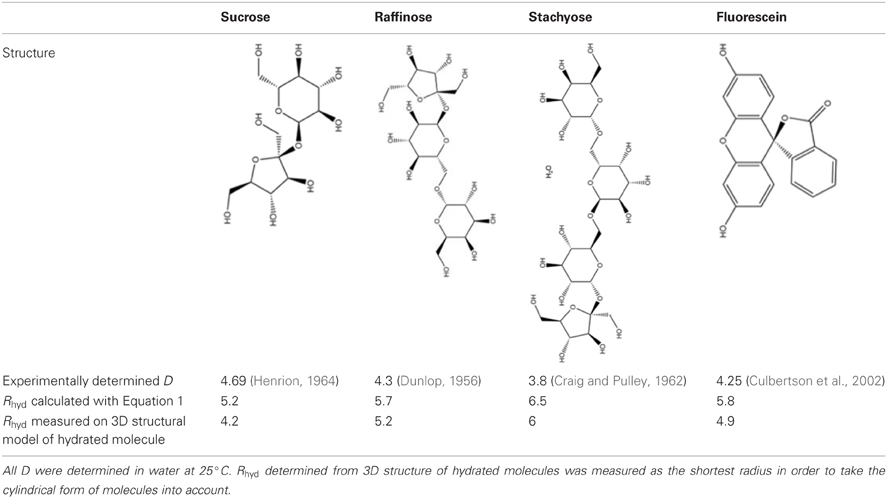
Table 1. Diffusion coefficients D and hydrodynamic radii Rhyd of relevant sugars and the fluorescent tracer fluorescein.
The Stokes–Einstein equation returns the radius of a sphere that diffuses at the same rate as the molecule in question. This might influence our considerations on filtering as the sugar molecules are not spherical but cylindrical in form. Therefore, measurement of hydrodynamic radius was performed on models of the hydrated molecules in the software ChemOffice3D. The shortest model radii of the three sugars are shorter than the calculated ones because of their cylindrical form, which results in a smaller difference between raffinose and stachyose (Table 1). Even though the different approaches yield slightly different hydrodynamic radii, the relative values are very similar, especially for the difference between sucrose and raffinose, which is decisive in our considerations. In the following, values for hydrodynamic radius derived from the molecular model are used as they closer reflect the actual dimensions of hydrated sugars.
The Substructure of Plasmodesmata
The ultrastructural analysis of PD has, so far, been limited to approaches using transmission electron microscopy (TEM; Roberts and Oparka, 2003). With optimal tissue preparation and imaging, structures inside PD were resolved to the extend that models of PD substructure could be proposed (e.g., Ding et al., 1992; Waigmann et al., 1997; Botha et al., 1993). Whereas all of the proposed models agree on the presence of a central desmotuble and plasma membrane lining the outer PD wall, they differ in the arrangement of particles that restrict the cytoplasm between desmotuble and plasma membrane. Freeze-substituted PD of developing tobacco leaves showed electron-dense particles attached to the desmotuble as well as to the outside of the plasma membrane in the neck region (Ding et al., 1992). Image overlays indicate that these particles restrict the cytoplasmic sleeve to channels of ~12.5 Å in radius. The central part of PD was found to be wider and spoke-like extensions were present between desmotuble and plasma membrane (Ding et al., 1992). Both features were also shown for the central part of conventionally fixed PD from pea roots (Schulz, 1995).
The neck region of tobacco leaf trichome PD differs from the mesophyll PD in that they do not have electron-dense particles attached to desmotuble and plasma membrane (Waigmann et al., 1997). Earlier experiments demonstrated a larger size-exclusion limit of the trichome PD compared to mesophyll PD (Waigmann and Zambryski, 1995), which might be enabled by the unobstructed sleeve structure (Waigmann et al., 1997). Extensive measurements of the neck region of PD in pea roots on 30 nm ultrathin sections revealed a half-sleeve width of 16 ± 0.18 Å for controls and different mannitol treatments (n = 205; Schulz, 1995).
The models with nano channels and cytoplasmic sleeve dominate the discussion of PD structure today, but alternative configurations are possible, as there are many structures that are not dense enough to be picked up by TEM. In nuclear pores, a hydrogel structure was shown to be instrumental to selective transport through the pore (Miao and Schulten, 2009). These hydrogel parts are not visible on TEM images (Panté, 2007; Maimon et al., 2012). In PD, no analogs to the flexible filamentous phenylalanine-glycine nucleopore proteins (FG-Nups) have been identified to date. These intrinsically disordered proteins form the backbone of the hydrogel in nuclear pores (Frey and Görlich, 2007; Terry and Wente, 2009; Mincer and Simon, 2011). However, in general, only relatively few PD proteins are known (Fernandez-Calvino et al., 2011), and approaches might not have been suitable to identify long-chained membrane-attached proteins. A hydrogel filling the cytoplasm in PD could potentially enhance their filtering capacity, as hydrogels act as molecular sieves (Amsden, 1998a; Dembczynski and Jankowski, 2000; Zhang and Amsden, 2006).
The structure of PD at the BSC-IC interface is unlike that of any other PD with the long narrow neck regions on the IC side appearing filled by the desmotuble on TEM images (Fisher, 1986; Turgeon et al., 1993; Volk et al., 1996). Small openings, below 1 nm, between PM and desmotuble are not expected to be resolved by TEM. Based on the PD models described above, we include three hypothetical configurations in the subsequent analysis of diffusional properties (Figure 1).
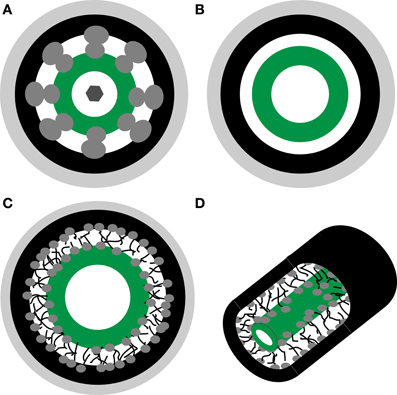
Figure 1. Schematic representations of hypothetical plasmodesmata substructure. (A) Nano channel model proposed by Ding et al. (1992). (B) Cytoplasmic sleeve model proposed by Waigmann et al. (1997). (C,D) Cytoplasmic sleeve filled by polymer-meshwork hydrogel. Light gray—cell wall, black—plasma membrane, dark gray—proteins, green—desmotuble.
Modeling Diffusion Hindrance in Plasmodesmata with Different Substructure
Diffusion through a pore is hydrodynamically constrained when the dimensions of a solute molecule are of the same order as those of the pore. To describe diffusion in this case, the hindrance factor H has to be included in Fick's law of diffusion:
with the flux per unit area J in mol μm−2 s−1, diffusion coefficient in bulk solution D0 in μm2 s−1, concentration potential delta c in mol μm−3 and the diffusion distance d in μm. The hindrance factor describes the relation of the apparent diffusion coefficient Da to the diffusion coefficient in bulk solution D0.
Many different models were proposed to describe diffusion under various conditions. In the following, the three most relevant models that describe the potential configurations of PD (Figure 1) are applied to assess relative hindrance of sucrose, raffinose, and stachyose.
Sub-nano channels (Figure 1A)
Various models that describe hindered diffusion of molecules through liquid-filled pores are reviewed by Deen (1987) and Dechadilok and Deen (2006). We use the model proposed by Dechadilok and Deen (2006), which is a slightly extended version of the model that was provided by Higdon and Muldowney (1995). The decisive factor is the relative size of solute to pore radius .
This model accounts for the effects of particle-wall hydrodynamic interactions and steric restrictions on diffusion of a neutral particle through pores that are several times longer than wide. The model covers a wide range of λ.
The hindrance factor for sucrose, raffinose, and stachyose in dependence of the channel radius are given in Figure 2A. At 20 Å channel radius the apparent diffusion of sucrose is reduced to one third of the value in bulk solution. Diffusion of raffinose and stachyose is only slightly more hindered compared to bulk solution with 20 and 26% respectively. A 1000-fold reduction of diffusion is realized at 5.4 Å for sucrose, 6.5 Å for raffinose, and 7.6 Å for stachyose, i.e., close to the molecular size cut-off. At the stachyose cut-off of 6.1 Å, raffinose diffusion is hindered 60 times more than sucrose.
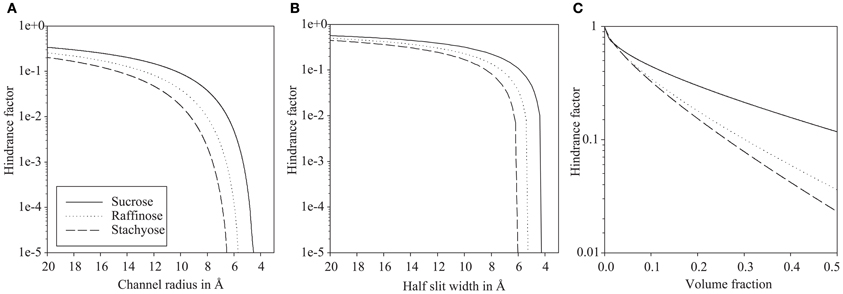
Figure 2. Logarithmic scale plots of diffusion hindrance in relation to hypothetical plasmodesmata substructure configurations. Hindrance factor for sucrose, raffinose, and stachyose increases faster with smaller dimensions in single plasmodesmal channels (A) than in a cytoplasmic sleeve (B). Hindrance in hydrogels (C) is moderate, even at high volume fractions.
The results are virtually identical to values calculated with the model provided by Mavrovouniotis and Brenner (1988), which is specifically developed for cases where the channel radius rc is only slightly larger than the radius rs of the diffusing solute (data not shown).
Slit (Figure 1B)
The cytoplasmic sleeve forms a ring between PM and desmotuble with very small width compared to the ring diameter and can therefore be described as a slit. An analytical solution to describe diffusion through slits was provided by Dechadilok and Deen (2006). Lambda is here the relative size of the solute molecule to half slit width h:.
As shown in Figure 2B, diffusion hindrance is moderate for a slit of 20 Å half-width with reduction to 57% for sucrose, to 50% for raffinose, and to 45% for stachyose diffusion. A 1000-fold reduction of diffusivity is first realized at half-width of 4.4, 5.4, and 6.2 Å for sucrose, raffinose, and stachyose, respectively. At the cut-off of stachyose of 6.1 Å, raffinose diffusion is hindered three times more than sucrose.
Compared to the sub-nano channels, the relative hindrance of raffinose and stachyose in relation to hindrance of sucrose is lower at larger radii/slit width, but close to the molecular cut-off, relative hindrance is an order of magnitude higher than in the channel configuration (Figure 2B).
Hydrogel (Figures 1C,D)
Models that describe hindered diffusion through hydrogels are reviewed by Amsden (1998b) and Waters and Frank (2009). The parameters that influence hindrance are the polymer volume fraction and polymer fiber radius. We use the model described by Philips, as it combines terms for hydrodynamic interactions and obstruction effects and was shown to fit experimental data over a wide range of parameter values (Phillips, 2000).
Term explanation: ratio of fiber radius to solute radius , adjusted volume fraction , Φ is actual polymer volume fraction. We used a polymer fiber radius rf of 15 Å for calculations, anticipating protein filaments, similar to the ones found in the nuclear pore outer area (Mincer and Simon, 2011).
Hindrance of such a hydrogel for small molecules, like the sugars in question here, is moderate (Figure 2C). Even at extremely high volume fractions, sucrose diffusion is reduced by less than 10 times and raffinose and stachyose less than 50 times. A volume fraction of 0.5 actually means that half the gel volume is filled with polymers. Typical volume fractions of hydrogels are below 0.2 (Amsden, 1998b), the FG-repeats in the nuclear pore make up between 0.12 and 0.2 of the pore volume (Frey and Görlich, 2007).
The calculations only apply to a pure hydrogel. In PD, it could be expected that a hydrogel would fill up the space within a sub-nano channel or sleeve. The hindrance effects of the gel would then be increased by wall effects, similar to the ones described in the previous sections. Since no information is available on the exact geometries of either the cytosolic cross-section in the PD neck region or the hydrogel properties, we do not attempt to accommodate the combined effect of channel/slit- and hydrogel diffusion hindrance in our considerations.
When half the gel space is taken up by polymers, raffinose diffusion is hindered 3.2 times more than sucrose. Relative hindrance of raffinose and stachyose in relation to hindrance of sucrose is, even at extremely high volume fractions, several orders of magnitude lower than relative hindrance of sub-nano channel and slit configurations with low radius/slit width.
It can be concluded that efficient filtering is only possible in sub-nano channels and slit when the channel radius or half slit width is very close to the hydrodynamic radius of raffinose and stachyose. Hydrogels, even at very high polymer volume fraction, show only a modest relative hindrance.
Theoretical Data Matches the Experimentally Determined Diffusion Coefficient
In order to test if the theoretical data on hindrance in the three hypothetical configurations is physiologically relevant, it was compared to the experimentally determined diffusion coefficient of the PD at this specific interface. The effective diffusion coefficient for the fluorescent tracer molecule fluorescein was determined with live-cell photoactivation microscopy as described in Appendix. Fluorescein has a hydrodynamic radius of 4.9 Å, as determined with ChemOffice Pro, meaning that its size lies between sucrose and raffinose (Table 1).
Determination of the apparent diffusion coefficient across the cell wall between IC and BSC in Cucurbita pepo with photoactivation microscopy yields a value of 0.41 μm2 s−1 for fluorescein. The value is actually very close to the diffusion coefficient across the cell wall between mesophyll cells, which is around 0.5 μm2 s−1 assuming a cell wall thickness of 0.1 μm (Liesche and Schulz, 2012b). Compared to diffusion in water, these values are about 10 times lower.
The effective diffusion coefficient Deff per PD is calculated from the hindrance factors calculated above by,
with x the number of PD per μm2 cell wall interface, H the hindrance factor and Dcyt the cytosolic diffusion coefficient. The cytosolic diffusion coefficient can be assumed to be two times lower than that in water, based on measurements using electron spin resonance (Mastro et al., 1984) or fluorescent tracers (Liesche, unpublished data). In case of sub-nano channels, the value has to be additionally multiplied by the number of channels per PD. Volk et al. (1996) calculated a PD frequency on the IC-side of Cucumis melo of 14 PD per μm2. A similar value can be estimated from Cucurbita pepo micrographs (Turgeon et al., 1975). The value refers to PD on the IC-side, which are, due to their narrower diameter, likely to be transport-limiting.
We chose the experimental value of 0.41 μm2 s−1 to find PD configurations where the theoretical model would yield a matching diffusion coefficient. With 14 PD per μm2, a slit would need to have a half width of 5.2 Å to match the effective diffusion coefficient, whereas a hydrogel even at just below 0.5 volume fraction would match this value. Results for the sub-nano channel configuration are plotted in Figure 3 to show which combination of channel radius and number of sub-nano channels per PD, the experimental value is met. At nine channels, suggested by Terry and Robards (1987) for Abutilon nectary trichome cells, each channel would need to have a radius of 6.4 Å.
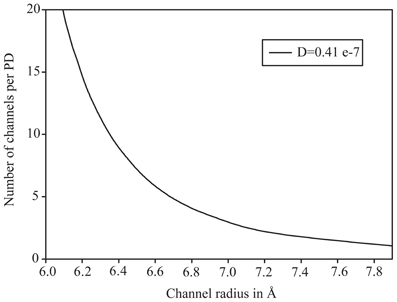
Figure 3. Plot of effective diffusion coefficient for diffusion of fluorescein through plasmodesmata with sub-nano channel configuration. The curve shows at which combination of number of channels and channel radius the experimentally determined value is matched.
The extremely restricted diffusion as considered in the theoretical models does fit experimental data. Since the effective diffusion coefficient is quite low, it is met even when hindrance is very high, because of the high number of PD at this interface.
Testing Filtering Efficiency and Physiological Relevance of the Modeled PD Configurations with Literature Values
Using literature values for sugar concentration potentials between IC and BSC, we can test if the model configurations at which the effective diffusion coefficient Deff matches experimental data would enable efficient filtering. In order to test whether the model parameters are feasible, we have tested the models with literature values of sucrose flux into the phloem.
Haritatos et al. (1996) provided values for the concentration of different sugars in the sieve element-IC complex and leaf mesophyll in Cucumis melo. The concentration of sugars in the IC is generally assumed to be similar to that in sieve elements as they are connected via wide PD. Similarly, the concentration in BSC can be assumed to be similar to the rest of the mesophyll cells, because of their high cytosolic coupling (Liesche and Schulz, 2012a). The authors found the concentration of raffinose and stachyose in mesophyll cells to be virtually 0 (Haritatos et al., 1996). Based on the concentration values, a potential across the BSC-IC interface of 67 mM for raffinose and 334 mM for stachyose can be calculated. The sucrose concentration potential in the cytosol between mesophyll and IC in Cucumis melo was determined as 60 mM (Haritatos et al., 1996).
The only values for vein loading rates in mature leaves of an active symplasmic loader that we are aware of are provided by Schmitz et al. (1987) for Cucumis melo. Leaf export rate as determined with 14CO2 labeling experiments was 4.25 mg (CH2O) per dm2 of leaf per h. Since the BSC-IC interface area in 1 dm2 of leaf is given as 3558 mm2, the flux across this interface was calculated to be 1.1 × 10−5 (CH2O) or 9.7 × 10−7 mol sucrose m−2 s−1mol sucrose. This value is in the range of comparable values reported for flux across the BSC-companion cell interface in active apoplasmic and passive symplasmic loading species (Table 2). The value is furthermore one order of magnitude lower than flux out of sieve elements in phloem unloading in the root tip of peas, which is entirely symplasmic (Schulz, 1998).
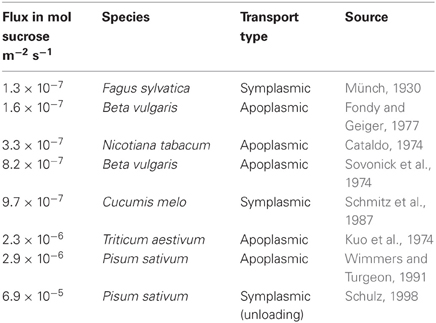
Table 2. Sucrose flux rates across the bundle sheath-companion cell interface reported in the literature.
Sugar flux using the hindrance factors that were determined for the different hypothetical PD configurations is calculated with Equation 2. Rearrangement of Equation 2 to,
allows for calculation of sugar concentration potential. A diffusion distance of d = 0.18 μm corresponding to the length of the neck region, as measured by Fisher (1986) in Coleus blumei, was assumed. The rest of the PD is considerably wider and therefore not likely to be transport-limiting.
Assuming a sub-nano channel configuration with 9 channels of 6.4 Å radius, the literature values for sugar concentration potential would lead to flux across the BSE-IC interface of 58 × 10−12 mol m−2 s−1 and 1.2 × 10−12 mol m−2 s−1 for raffinose and stachyose, respectively, while allowing a sucrose flux of 860 × 10−12 mol m−2 s−1 (Figure 4A). The sucrose flux values from Cucumis melo (Schmitz et al., 1987) would be met by sub-nano channels at a potential of ~105 mM. The results are almost identical for sub-nano channel configurations with different combinations of channel number and radius as determined in Figure 3 (data not shown).
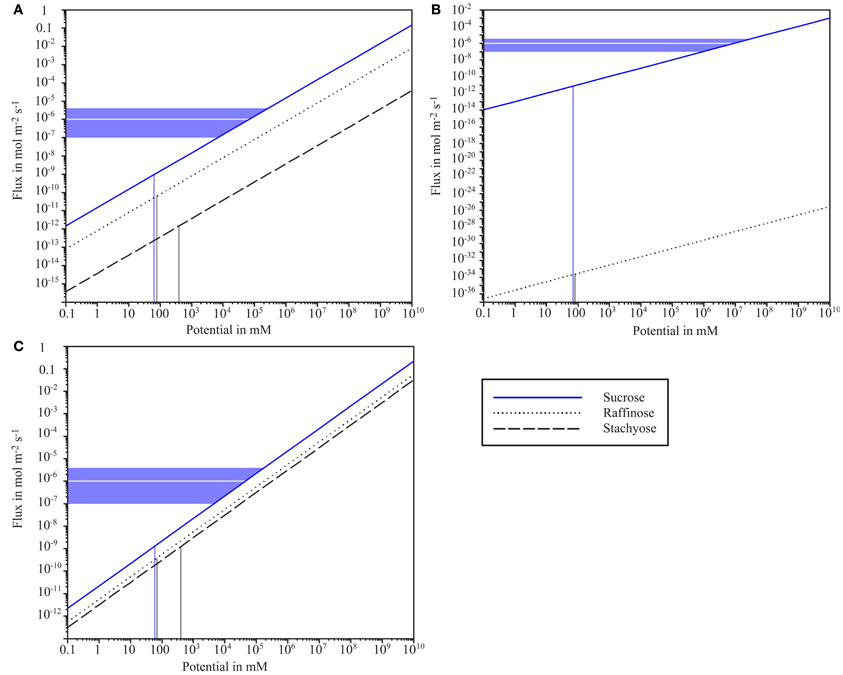
Figure 4. Logarithmic scale plot of sugar flux and concentration potential between bundle sheath cells and intermediary cells for different plasmodesmata configurations. (A) Sub-nano channel configuration assuming 9 channels with 6.5 Å radius. (B) Slit configuration assuming half slit width of 5.2 Å. (C) Hydrogel configuration assuming a polymer volume fraction of 0.49. Vertical lines indicate sugar concentration potentials as provided by Haritatos et al. (1996). Horizontal lines indicate sucrose flux values provided by Schmitz et al. (1987, gray) and a flux range based on values listed in Table 2 (blue). Raffinose flux is strongly hindered in the slit model in contrast to the other configurations, which would enable considerable “leakage” out of the intermediary cell. Hindrance of sucrose flux at concentration potentials observed by Haritatos et al. (1996) would in all models be orders of magnitude too high to realize flux rates reported by Schmitz et al. (1987) and other authors.
Assuming a slit configuration with 5.2 Å half-slit width, the concentration potentials given by Haritatos et al. (1996) would lead to an extremely low flux of raffinose with 2.4 × 10−34 mol m−2 s−1, while stachyose would be completely blocked (Figure 4B). Sucrose would flow into IC at a rate of 6.2 × 10−12 mmol m−2 s−1, which is several dimensions lower than flux across this interface as stated in the literature. The sucrose flux values provided for Cucumis melo (Schmitz et al., 1987) and the values calculated for other plant species (Table 2) would require an unrealistic potential of around 5 × 107 mM (Figure 4B).
Hydrogel-filled PD channels with a polymer volume fraction of 0.49 would enable flux of 0.4 × 10−9 mmol m−2 s−1 and 10−9 mol m−2 s−1 for raffinose and stachyose, respectively at the concentration potentials provided by Haritatos et al. (1996) (Figure 4C). The sucrose flux values from Cucumis melo (Schmitz et al., 1987) would be met by the hydrogel at a potential of around 5 × 104 mM (Figure 4C).
The calculations show the slit configuration as significantly more efficient filter for raffinose and stachyose than the other configurations. Conductance (flux/potential) is very similar for the sub-nano channel configuration and the hydrogel (Figures 4A,C). The slit model enables significantly less flux than the other configurations at a comparable potential (Figure 4B). Flux values are obviously far below the value that would be required to drive the observed flow through the theoretical PD configurations assumed here.
Discussion
The results of this study provide insight on four key questions regarding the feasibility of sugar filtering in active symplasmic phloem loading:
Can Plasmodesmata Discriminate Small Differences in Hydrodynamic Radius?
The theoretical considerations of diffusion hindrance through PD with hypothetical substructural configurations show that efficient filtering of raffinose and stachyose is feasible when the channel radius or slit width is very close to the physical size of the transportate. In principle this could be the case at the cell wall interface between BSC and IC in RFO-transporting plants. The relatively low diffusion coefficient for symplasmic transport across the BSC-IC interface in Cucurbita pepo that we determined experimentally, confirms that PD indeed have a very limited permeability. This can be explained by a restricted cross-sectional area per PD available for flow. The diffusion coefficient is a value integrated over all PD present at this crucial interface. One could argue that the observed values could also be due to a small number of relatively wide PD that enable the observed diffusion, while most of the very abundant PD in this interface would be completely blocked. We consider this alternative interpretation as very improbable. Accordingly, the experimental data support the hypothesis that PD at the BSC-IC interface are specialized and have a very small passage area for cytosolic compounds. For the sub-nano channel configuration we find a raffinose flux rate reduced to 6.7% that of sucrose. Values in this range were proposed to allow efficient RFO trapping according to Haritatos and Turgeon (1995). The authors calculated a raffinose permeation factor of 1.9% that of sucrose in PD pores of 7 Å radius. The relative permeation is not derived from flux rates but from a geometrical pore size factor. Nevertheless, this pore size factor is in principle comparable to our hindrance factors as it introduces the same effects of steric hindrance and wall interaction (although using different equations) into the diffusion equation.
Is Diffusion the Sole Mechanism of Pre-Phloem Transport in Active Symplasmic Loaders?
Although our modeling supports the possibility that PD in the BSC-IC interface fulfill the filtering function that has been ascribed to them as part of the polymer trap mechanism (Turgeon et al., 1993), comparison to literature values for sucrose flux into the IC does not seem to support this conclusion. The concentration potential that would be necessary to realize the flux into IC observed in Cucumis melo (Schmitz et al., 1987) would need to be orders of magnitude higher than what is physiologically feasible, especially in the slit configuration that would offer the best filtering efficiency. Even for the sub-nano channel model a potential of 105 mM would be needed to enable sufficient diffusional sucrose flux (see Figure 4A). This value is far higher than any sugar concentration potential between adjacent plant cells reported so far and about 1600 times higher than what has been calculated for the BSC-IC interface in Cucumis melo (Haritatos et al., 1996).
It should be noted that the methodology could have influence on the discrepancy between the values for diffusion coefficient and sucrose flux. In contrast to the sugar molecules, the fluorescent tracer used here carries a negative charge, potentially altering intra-PD diffusion kinetics. While it is generally assumed that only the hydrodynamic radius influences passage through PD (Terry and Robards, 1987), one study reported minimally reduced diffusion of charged GFP compared to neutral GFP (Dashevskaya et al., 2008). Nevertheless, it is extremely unlikely that sucrose diffuses thousands of times faster than a charged molecule of the same hydrodynamic radius, which would be necessary to reconcile diffusion and flux values.
Another factor that influences the calculations is the length of restricting part of the PD (d in Equation 8). If it was half as long as assumed here, flux would be twice as high. However, electron micrographs have shown the whole part of the PD on the IC side to be “narrow” and no special protein aggregations have been reported that could suggest more local restrictions.
How can the fact that diffusion driven by a concentration potential is insufficient to realize the observed sucrose flux rates be explained? Wider PD could be possible if the filtering would not depend on size-exclusion based on the hydrodynamic radius, but were realized instead by a gating mechanism. Such a mechanism is implied in the case that PD transport compounds unidirectional, as has been demonstrated for tobacco leaf trichomes (Christensen et al., 2009). A solely unidirectional mechanism can, however, be excluded here according to preliminary experiments with uncaging of fluorescent tracers that were passing the BSC-IC interface in both directions (Liesche, unpublished data).
RFO concentrations in the BSC used in the present study to determine the concentration potentials are very small which is taken as argument for efficient filtering. However, the capacity for raffinose and stachyose breakdown in BSC would allow wider, i.e., less restrictive PD. Alpha-galactosidase activity has been demonstrated in the leaves of the Cucurbitaceae, although strongly declining after sink-source transition (Pharr and Sox, 1984; Gaudreault and Webb, 1986). If enzymatic breakdown could happen fast enough in the BSC, it could compensate for RFO “leakage” due to less efficient filtering. This should be tested, for example by BSC-specific gene expression analysis and in vitro activity assays.
In conclusion, the transport of sucrose from mesophyll into IC cannot solely be driven by diffusion, though particular adaptations of the PD substructure, such as a gating mechanism or filling of the sub-nano channels with hydrogel, and the enzymatic activity in BSC would reduce the discrepancy between flux rate and the postulated differences in concentration potential of the sugars involved.
Does Apoplasmic Sucrose Loading into Intermediary Cells Complement Symplasmic Transport?
For the polymer trap hypothesis it is important that the narrow PD allow sucrose to enter the IC with a rate sufficient to match the phloem export of RFO sugars. It could be argued that insufficient symplasmic sucrose transport is complemented by apoplasmic sucrose uptake into IC, and that the main function of the specific PD is to restrict leakage of RFO back into the BSC. AP-chloromercuribenzene-sulfonic acid (PCMBS), an inhibitor of sugar transporters was shown to significantly reduce phloem loading in Cucurbita pepo using C-11 (Thorpe and Minchin, 1988). However, this observation, and thus the possibility for additional apoplasmic sucrose uptake is contradicted by a number of thorough PCMBS studies on active symplasmic loaders which do not show a reduction of phloem loading (cf. Weisberg et al., 1988; van Bel et al., 1993; Turgeon and Medville, 2004), and by the downregulation of sucrose transporters which had almost no effect on phloem loading (Zhang and Turgeon, 2009). Moreover, PCMBS does not only block sugar transporters, but also aquaporins that are important for the osmotic uptake of water into the SECCC (Heinen et al., 2009). Obviously, this possible side effect has to be considered in the interpretation of PCMBS data.
Can the Reported Flux Rates Across the BSC-IC Interface be Explained with Bulk-Flow?
As alternative to diffusion, it has been hypothesized that sucrose enters IC by bulk flow. Voitsekhovskaya et al. (2006), who could not detect a cytosolic sucrose concentration potential along the pre-phloem pathway of the symplastic loader Alonsoa merionalis, speculated that the negative water potential in the phloem draws water from the bundle sheath. This could create a mass flow that moves sucrose into the phloem, while preventing diffusion toward the mesophyll. A number of factors have influence on the hydrostatic pressure of each of the cells on the pre-phloem transport pathway, such as cytosolic and vacuolar sugar concentration, conversion into transitional starch in chloroplasts, water potential in the apoplast and its domains, frequency, and distribution of aquaporins, extensibility of the cell wall and last not least the frequency and permeability of PD. We can assume a well-regulated sucrose homeostasis in these cells with set values that balance concentration potentials with osmotic water uptake not only in active, but even more so in passive symplasmic loaders, such as gymnosperm trees (see Liesche et al., 2011; Liesche and Schulz, 2012a). Bulk flow from mesophyll into the sieve elements is as well-postulated for passive symplasmic loading angiosperm trees (Turgeon, 2010; Fu et al., 2011). It is interesting to note that, irrespective of the loading mode, sucrose flux rates across the BSC-IC interface, respectively that between BSC and companion cell-sieve element complex are very similar (Table 2).
With regard to active symplasmic loaders, we plan to test the bulk flow hypothesis, characterize the minor vein apoplasm with apoplasmic tracers and determine whether the PD-mediated cell wall permeability of the BSC-IC interface is significantly higher for the transport into the IC than from IC to BSC. This would indicate that flow is not simply diffusive but somehow favored toward the IC direction.
The results show that important questions regarding the mechanism of active symplasmic phloem loading remain unsolved. There is no doubt that the distinctive PD at the BSC-IC interface play a significant role in phloem loading. The experimentally determined comparatively low diffusion coefficient across the BSC-IC interface together with the high PD abundance shown in all TEM investigations of active symplasmic loaders is consistent with the interpretation that they are bottle necks in symplasmic transport, and that tri- and tetrasaccharides experience a significantly larger hindrance through these PD than sucrose. The data provided here indicates that additional factors are yet to be discovered that enable efficient sugar filtering while also allowing sufficiently high sucrose transport rates.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Robert Turgeon, Cornell University, for discussion of PD abundance at the BSC-IC interface. Microscopic imaging and image processing was performed at the Center for Advanced Bioimaging Denmark, located at the University of Copenhagen.
References
Amsden, B. (1998a). Solute diffusion in hydrogels. an examination of the retardation effect. Polym. Gels Netw. 6, 13–43. doi: 10.1016/S0966-7822(97)00012-9
Amsden, B. (1998b). Solute diffusion within hydrogels. Mech. Models Macromol. 31, 8382–8395. doi: 10.1021/ma980765f
Beebe, D. U., and Turgeon, R. (1992). Localization of galactinol, raffinose, and stachyose synthesis in Cucurbita pepo leaves. Planta 188, 354–361. doi: 10.1007/BF00192802
Botha, C. E. J., Hartley, B. J., and Cross, R. H. M. (1993). The ultrastructure and computer-enhanced digital image-analysis of plasmodesmata at the Kranz mesophyll-bundle sheath interface of Themeda triandra var imberbis (Retz) A. Camus in conventionally-fixed leaf blades. Ann. Bot. 72, 255–261.
Cataldo, D. A. (1974). Vein loading: the role of the symplast in intercellular transport of carbohydrate between the mesophyll and minor veins of tobacco leaves. Plant Physiol. 53, 912–917. doi: 10.1104/pp.53.6.912
Christensen, N. M., Faulkner, C., and Oparka, K. (2009). Evidence for unidirectional flow through plasmodesmata. Plant Physiol. 150, 96–104. doi: 10.1104/pp.109.137083
Craig, L. C., and Pulley, A. O. (1962). Dialysis studies 4. Preliminary experiments with sugars. Biochemistry 1, 89. doi: 10.1021/bi00907a014
Culbertson, C. T., Jacobson, S. C., and Ramsey, J. M. (2002). Diffusion coefficient measurements in microfluidic devices. Talanta 56, 365–373. doi: 10.1016/S0039-9140(01)00602-6
Dashevskaya, S., Kopito, R. B., Friedman, R., Elbaum, M., and Epel, B. L. (2008). Diffusion of anionic and neutral GFP derivatives through plasmodesmata in epidermal cells of Nicotiana benthamiana. Protoplasma 234, 13–23. doi: 10.1007/s00709-008-0014-7
Davidson, A., Keller, F., and Turgeon, R. (2011). Phloem loading, plant growth form, and climate. Protoplasma 248, 153–163. doi: 10.1007/s00709-010-0240-7
Dechadilok, P., and Deen, W. M. (2006). Hindrance factors for diffusion and convection in pores. Ind. Eng. Chem. Res. 45, 6953–6959. doi: 10.1021/ie051387n
Deen, W. M. (1987). Hindered transport of large molecules in liquid-filled pores. AIChE J. 33, 1409–1425. doi: 10.1002/aic.690330902
Dembczynski, R., and Jankowski, T. (2000). Characterisation of small molecules diffusion in hydrogel-membrane liquid-core capsules. Biochem. Eng. J. 6, 41–44. doi: 10.1016/S1369-703X(00)00070-X
Ding, B., Turgeon, R., and Parthasarathy, M. V. (1992). Substructure of freeze-substituted plasmodesmata. Protoplasma 169, 28–41. doi: 10.1007/BF01343367
Dunlop, P. J. (1956). The concentration dependence of the diffusion coefficient of raffinose in dilute aqueous solution at 25-degrees. J. Phys. Chem. 60, 1464–1465.
Fernandez-Calvino, L., Faulkner, C., Walshaw, J., Saalbach, G., Bayer, E., Benitez-Alfonso, Y., et al. (2011). Arabidopsis plasmodesmal proteome. PLoS ONE 6:e18880. doi: 10.1371/journal.pone.0018880
Fisher, D. G. (1986). Ultrastructure, plasmodesmatal frequency, and solute concentration in green areas of variegated Coleus blumei benth leaves. Planta 169, 141–152. doi: 10.1007/BF00392308
Fondy, B. R., and Geiger, D. R. (1977). Sugar selectivity and other characteristics of phloem loading in Beta vulgaris L. Plant Physiol. 59, 953–960. doi: 10.1104/pp.59.5.953
Frey, S., and Görlich, D. (2007). A saturated FG-repeat hydrogel can reproduce the permeability properties of nuclear pore complexes. Cell 130, 512–523. doi: 10.1016/j.cell.2007.06.024
Fu, Q., Cheng, L., Guo, Y., and Turgeon, R. (2011). Phloem loading strategies in relation to water relations in trees and herbaceous plants. Plant Physiol. 157, 1518–1527. doi: 10.1104/pp.111.184820
Gaudreault, P. R., and Webb, J. A. (1986). Alkaline alpha-galactosidase activity and galactose metabolism in the family Cucurbitaceae. Plant Sci. 45, 71–75. doi: 10.1016/0168-9452(86)90039-7
Hannah, M. A., Zuther, E., Buchel, K., and Heyer, A. G. (2006). Transport and metabolism of raffinose family oligosaccharides in transgenic potato. J. Exp. Bot. 57, 3801–3811. doi: 10.1093/jxb/erl152
Haritatos, E., Ayre, B. G., and Turgeon, R. (2000). Identification of phloem involved in assimilate loading in leaves by the activity of the galactinol synthase promoter. Plant Physiol. 123, 929–937. doi: 10.1104/pp.123.3.929
Haritatos, E., Keller, F., and Turgeon, R. (1996). Raffinose oligosaccharide concentrations measured in individual cell and tissue types in Cucumis melo L. leaves: implications for phloem loading. Planta 198, 614–622. doi: 10.1007/BF00262649
Haritatos, E., and Turgeon, R. (1995). “Symplastic phloem loading by polymer trapping,” in First International Symposium on Sucrose Metabolism, eds E. Echeverria, G. L. Salerno, and H. G. Pontis (Rockville, MD: American Society of Plant Physiologists), 216–224.
Heinen, R. B., Ye, Q., and Chaumont, F. (2009). Role of aquaporins in leaf physiology. J. Exp. Bot. 60, 2971–2985. doi: 10.1093/jxb/erp171
Henrion, P. N. (1964). Diffusion in sucrose plus water system. Trans. Faraday Soc. 60, 72. doi: 10.1039/TF9646000072
Higdon, J. J. L., and Muldowney, G. P. (1995). Resistance functions for spherical-particles, droplets and bubbles in cylindrical-tubes. J. Fluid Mech. 298, 193–210. doi: 10.1017/S0022112095003272
Kim, I., Cho, E., Crawford, K., Hempel, F. D., and Zambryski, P. C. (2005). Cell-to-cell movement of GFP during embryogenesis and early seedling development in Arabidopsis. Proc. Natl. Acad. Sci. U.S.A. 102, 2227–2231. doi: 10.1073/pnas.0409193102
Kuo, J., Canny, M. J., and Obrien, T. P. (1974). Pit-field distribution, plasmodesmatal frequency, and assimilate flux in mestome sheath-cells of wheat leaves. Planta 121, 97–118. doi: 10.1007/BF00388750
Liesche, J., Martens, H. J., and Schulz, A. (2011). Symplasmic transport and phloem loading in gymnosperm leaves. Protoplasma 248, 181–190. doi: 10.1007/s00709-010-0239-0
Liesche, J., and Schulz, A. (2012a). In vivo quantification of cell coupling in plants with different phloem-loading strategies. Plant Physiol. 159, 355–365. doi: 10.1104/pp.112.195115
Liesche, J., and Schulz, A. (2012b). Quantification of plant cell coupling with three-dimensional photoactivation microscopy. J. Microsc. 247, 2–9. doi: 10.1111/j.1365-2818.2011.03584.x
Liesche, J., and Schulz, A. (2013). “Symplasmic transport in phloem loading and unloading,” in Symplasmic Transport in Vascular Plants, eds P. Sowinski and K. Sokolovska (New York, NY: Springer), 165–196. doi: 10.1111/j.1365-313X.2004.02298.x
Maimon, T., Elad, N., Dahan, I., and Medalia, O. (2012). The human nuclear pore complex as revealed by cryo-electron tomography. Structure 20, 998–1006. doi: 10.1016/j.str.2012.03.025
Mastro, A. M., Babich, M. A., Taylor, W. D., and Keith, A. D. (1984). Diffusion of a small molecule in the cytoplasm of mammalian cells. Proc. Natl. Acad. Sci. U.S.A. 81, 3414–3418.
Maule, A. J., Benitez-Alfonso, Y., and Faulkner, C. (2011). Plasmodesmata–membrane tunnels with attitude. Curr. Opin. Plant Biol. 14, 683–690. doi: 10.1016/j.pbi.2011.07.007
Mavrovouniotis, G. M., and Brenner, H. (1988). Hindered sedimentation, diffusion, and dispersion coefficients for brownian spheres in circular cylindrical pores. J. Colloid Inter. Sci. 124, 269–283. doi: 10.1016/0021-9797(88)90348-7
McCaskill, A., and Turgeon, R. (2007). Phloem loading in Verbascum phoeniceum L. depends on the synthesis of raffinose-family oligosaccharides. Proc. Natl. Acad. Sci. U.S.A. 104, 19619–19624. doi: 10.1073/pnas.0707368104
Miao, L. L., and Schulten, K. (2009). Transport-related structures and processes of the nuclear pore complex studied through molecular dynamics. Structure 17, 449–459. doi: 10.1016/j.str.2008.12.021
Mincer, J. S., and Simon, S. M. (2011). Simulations of nuclear pore transport yield mechanistic insights and quantitative predictions. Proc. Natl. Acad. Sci. U.S.A. 108, E351–E358. doi: 10.1073/pnas.1104521108
Panté, N. (2007). “Contribution of electron microscopy to the study of the nuclear pore complex structure, composition, and function,” in Modern Research and Educational Topics in Microscopy, eds A. Mendez-Vilas and J. Diaz (Madrid: Formatex), 144–153.
Pappenheimer, J. R. (1953). Passage of molecules through capillary walls. Physiol. Rev. 33, 387–423.
Pharr, D. M., and Sox, H. N. (1984). Changes in carbohydrate and enzyme levels during the sink to source transition of leaves of Cucumis sativus L., a stachyose translocator. Plant Sci. Lett. 35, 187–193. doi: 10.1016/0304-4211(84)90227-X
Phillips, R. J. (2000). A hydrodynamic model for hindered diffusion of proteins and micelles in hydrogels. Biophys. J. 79, 3350–3353. doi: 10.1016/S0006-3495(00)76566-0
Rennie, E. A., and Turgeon, R. (2009). A comprehensive picture of phloem loading strategies. Proc. Natl. Acad. Sci. U.S.A. 106, 14162–14167. doi: 10.1073/pnas.0902279106
Roberts, A. G., and Oparka, K. J. (2003). Plasmodesmata and the control of symplastic transport. Plant Cell Environ. 26, 103–124. doi: 10.1046/j.1365-3040.2003.00950.x
Schmitz, K., Cuypers, B., and Moll, M. (1987). Pathway of assimilate transfer between mesophyll-cells and minor veins in leaves of Cucumis melo L. Planta 171, 19–29. doi: 10.1007/BF00395064
Schultz, S. G., and Solomon, A. K. (1961). Determination of effective hydrodynamic radii of small molecules by viscometry. J. Gen. Physiol. 44, 1189.
Schulz, A. (1995). Plasmodesmal widening accompanies the short-term increase in symplasmic phloem unloading in pea root-tips under osmotic-stress. Protoplasma 188, 22–37. doi: 10.1007/BF01276793
Sovonick, S. A., Geiger, D. R., and Fellows, R. J. (1974). Evidence for active phloem loading in minor veins of sugar beet. Plant Physiol. 54, 886–891.
Terry, B. R., and Robards, A. W. (1987). Hydrodynamic radius alone governs the mobility of molecules through plasmodesmata. Planta 171, 145–157. doi: 10.1007/BF00391090
Terry, L. J., and Wente, S. R. (2009). Flexible Gates: dynamic topologies and functions for FG nucleoporins in nucleocytoplasmic transport. Eukaryot. Cell 8, 1814–1827. doi: 10.1128/EC.00225-09
Thorpe, M. R., and Minchin, P. E. H. (1988). Phloem loading and transport of endogenously or exogenously labeled photo-assimilate in bean, beet, maize and cucurbit. J. Exp. Bot. 39, 1709–1721. doi: 10.1093/jxb/39.12.1709
Turgeon, R. (2010). The role of phloem loading reconsidered. Plant Physiol. 152, 1817–1823. doi: 10.1104/pp.110.153023
Turgeon, R., Beebe, D. U., and Gowan, E. (1993). The intermediary cell–minor-vein anatomy and raffinose oligosaccharide synthesis in the Scrophulariaceae. Planta 191, 446–456. doi: 10.1007/BF00195746
Turgeon, R., and Hepler, P. K. (1989). Symplastic continuity between mesophyll and companion cells in minor veins of mature Cucurbita pepo L. leaves. Planta 179, 24–31. doi: 10.1007/BF00395767
Turgeon, R., and Medville, R. (2004). Phloem loading. A reevaluation of the relationship between plasmodesmatal frequencies and loading strategies. Plant Physiol. 136, 3795–3803. doi: 10.1104/pp.104.042036
Turgeon, R., Webb, J. A., and Evert, R. F. (1975). Ultrastructure of minor veins in Cucurbita pepo leaves. Protoplasma 83, 217–232. doi: 10.1007/BF01282555
van Bel, A. J. E., Ammerlaan, A., and van Dijk, A. A. (1993). A three-step screening procedure to identify the mode of phloem loading in intact leaves: evidence for symplasmic and apoplasmic phloem loading associated with the type of companion cell. Planta 192, 31–39. doi: 10.1007/BF00198689
Voitsekhovskaya, O. V., Koroleva, O. A., Batashev, D. R., Knop, C., Tomos, A. D., Gamalei, Y. V., et al. (2006). Phloem loading in two Scrophulariaceae species. What can drive symplastic flow via plasmodesmata? Plant Physiol. 140, 383–395. doi: 10.1104/pp.105.068312
Volk, G. M., Haritatos, E. E., and Turgeon, R. (2003). Galactinol synthase gene expression in melon. J. Am. Soc. Hortic. Sci. 128, 8–15.
Volk, G. M., Turgeon, R., and Beebe, D. U. (1996). Secondary plasmodesmata formation in the minor-vein phloem of Cucumis melo L and Cucurbita pepo L. Planta 199, 425–432. doi: 10.1007/BF00195735
Waigmann, E., Turner, A., Peart, J., Roberts, K., and Zambryski, P. (1997). Ultrastructural analysis of leaf trichome plasmodesmata reveals major differences from mesophyll plasmodesmata. Planta 203, 75–84.
Waigmann, E., and Zambryski, P. (1995). Tobacco mosaic-virus movement protein-mediated movement of macromolecules through trichome plasmodesmata. J. Cell. Biochem. 7, 149–149.
Waters, D. J., and Frank, C. W. (2009). Hindered diffusion of oligosaccharides in high strength poly(ethylene glycol)/poly(acrylic acid) interpenetrating network hydrogels: hydrodynamic vs. obstruction models. Polymer 50, 6331–6339. doi: 10.1016/j.polymer.2009.05.034
Weisberg, L. A., Wimmers, L. E., and Turgeon, R. (1988). Photoassimilate transport characteristics of nonchlorophyllous and green tissue in variegated leaves of Coleus blumei Benth. Planta 175, 1–8. doi: 10.1007/BF00402875
Wimmers, L. E., and Turgeon, R. (1991). Transfer cells and solute uptake in minor veins of Pisum sativum leaves. Planta 186, 2–12. doi: 10.1007/BF00201491
Zhang, C., and Turgeon, R. (2009). Downregulating the sucrose transporter VpSUT1 in Verbascum phoeniceum does not inhibit phloem loading. Proc. Natl. Acad. Sci. U.S.A. 106, 18849–18854. doi: 10.1073/pnas.0904189106
Zhang, Y., and Amsden, B. G. (2006). Application of an obstruction-scaling model to diffusion of vitamin B-12 and proteins in semidilute alginate solutions. Macromolecules 39, 1073–1078. doi: 10.1021/ma0522357
Appendix
Experimental Determination of the Diffusion Coefficient of Fluorescein at the Intermediary Cell-Bundle Sheath Cell Wall Interface
The experimental procedure to determine the diffusion coefficient at the BSC-IC interface in the active symplasmic loader Cucurbita pepo was very similar to the quantification of PD-mediate cell wall permeability between Cucurbita maxima leaf mesophyll cells as described by Liesche and Schulz (2012b). Briefly, the photoactivatable tracer caged fluorescein (Invitrogen, USA) is applied to the target tissue, where it is taken up passively into all cells. Installing the tissue, in this case a whole leaf still attached to the plant, on a microscope, the tracer can then be activated by UV illumination in a specific target cell and its spread to neighboring cells monitored (Figure A1). The use of a confocal microscope equipped with resonant scanner (SP5, Leica Microsystems, Germany) allows for collection of three-dimensional data with high signal-to-noise ratio combined with high speed acquisition. From 3D time series all necessary functional and anatomical data for each individual cell can be gathered. The effective diffusion coefficient is calculated with Fick's law of diffusion.
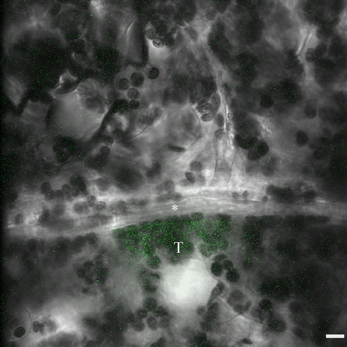
Figure A1. Confocal image of a photoactivation experiment in a Cucurbita pepo leaf. The image shows a single optical section of a 30 μm thick z-stack that was recorded at one time point during the 10 s-long photoactivation phase. The fluorescence of the activated tracer is displayed as extended focus projection in green, overlaid over the brightfield image. In image analysis, three-dimensional regions of interest are drawn adjacent to the cell wall between the bundle sheath target cell (T) and the intermediary cell (*) in order to quantify diffusion of activated tracer. Scale bar: 10 μm.
The effective diffusion coefficient was determined to be 4.087e-7, standard deviation 2.878e-7, standard error 1.439e-7, n = 4.
As experiments were performed, it could not be discriminated between IC and phloem parenchyma cells, which can have a similar shape as IC and are also located adjacent to BSC (see Figure 1A in Turgeon and Hepler, 1989). Instead, this was done during image processing, based on the very different ratio of cellular to vacuolar volume of the two cell types. Two populations corresponding to the two cell types were identified: one with the cytosol making up 31–56% of the cell volume, the other with less than 10% cytosol. Experiments that involved the latter cells were not considered as they are likely to be phloem parenchyma cells that are known to have a much larger vacuole than IC (Turgeon et al., 1975). A mix-up with companion cells that can be present in on the adaxial side of veins of C. pepo (Turgeon et al., 1975) can be excluded as imaging happened from the abaxial side and penetration depths was limited to 150–200 μm.
Keywords: phloem loading, plasmodesmata, polymer trap, hindered diffusion, carbon allocation
Citation: Liesche J and Schulz A (2013) Modeling the parameters for plasmodesmal sugar filtering in active symplasmic phloem loaders. Front. Plant Sci. 4:207. doi: 10.3389/fpls.2013.00207
Received: 25 March 2013; Accepted: 31 May 2013;
Published online: 19 June 2013.
Edited by:
Aart Van Bel, Justus-Liebig-University Giessen, GermanyReviewed by:
John W. Patrick, The University of Newcastle, AustraliaRobert Turgeon, Cornell University, USA
Copyright © 2013 Liesche and Schulz. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and subject to any copyright notices concerning any third-party graphics etc.
*Correspondence: Johannes Liesche, Department of Plant and Environmental Sciences, University of Copenhagen, Thorvaldsensvej 40, 1871 Frederiksberg, Copenhagen, Denmark e-mail:am9saUBsaWZlLmt1LmRr

