Hydraulic Balance of a Eucalyptus urophylla Plantation in Response to Periodic Drought in Low Subtropical China

A clear understanding of hydraulic regulation in cultivated plants is crucial for addressing challenges to forest water cycling due to climate changes in low subtropical China. Experiments were conducted to determine the hydrologic balance of a Eucalyptus urophylla plantation in response to periodic drought. Trees displayed lower stomatal conductance (G_S) and leaf water potentials (Ψ_L) during the dry periods. A decrease of 22.4% was found for the maximum reference G_S (G_S at D = 1 kPa; G_Sref-max). Accordingly, specific hydraulic conductivity (k_s) decreased by 45.3 – 65.6% from the wet to the dry season, depending on the tree size. Fairly stable leaf stomatal conductance (g_s) with decreasing Ψ_L (Ψ_L < -1.6 MPa) contributed to the high water-use efficiency (WUE) of this Eucalyptus species. Additionally, the lower stomatal sensitivity (-m = 0.53) in the dry season might also be responsible for the high WUE, since we found an anisohydric behavior that was associated with photosynthetically active radiation (Q₀). Larger trees were found to use water more efficiently than small trees, due to the higher sensitivity of k_s to decreasing Ψ_L. This was also verified by the decreasing leaf carbon isotope discrimination (Δ¹³C) with increasing tree diameter. However, further studies are needed to determine the universality of these results for other Eucalyptus species in this region.

Introduction

Due to anthropogenic climate changes, the survival of tropical and subtropical forest communities may be threatened in a variety of ways, including increased frequency of severe droughts caused by changes in precipitation pattern (Davidson et al., 2012), especially in the southern region of China (Zhai et al., 2005; Zhou et al., 2011). As previously reported, long term drought may lead to increased tree mortality, and decreased productivity and forest biomass carbon sinks for natural forests (Chaves et al., 2002; Zhou et al., 2013). Recently, planted forests have been suggested to be more vulnerable to severe environmental stress because of their weaker ecological resilience (Bleby et al., 2012).

Under light-saturating conditions and a high vapor pressure deficit (D), most plants reduce stomatal conductance (G_S) to limit transpiration and to slow down the development of potentially damaging low leaf water potential (Ψ_L) (Meinzer, 1993), ultimately leading to a decrease in net primary productivity (NPP) (Ryan and Waring, 1992). However, some plants have been hypothesized to follow optimal trajectories to maximize their carbon gain (Hölttä et al., 2011; Rosen, 2013). For example, Eucalyptus species have been reported to have high photosynthetic capacity, WUE, and growth rate (Whitehead and Beadle, 2004), which may imply a high canopy G_S. These characteristics may minimize and counteract the effects of extreme climate events, and reinforce community resilience (Lloret et al., 2012). However, how these species coordinate decreases in G_S to avoid hydraulic failure with the demand to maximize carbon assimilation in dry conditions is poorly understood and less reported.

Generally, plants have been classified into two broad categories based on the ability of stomata to regulate Ψ_L: isohydric and anisohydric (Jones, 1998; Martínez-Vilalta et al., 2014). Isohydric species adjust their stomatal opening in such a way as to maintain midday Ψ_L relatively stable as environmental conditions change. In contrast, anisohydric species have less strict stomatal control, with no discernible threshold of minimum Ψ_L (Martínez-Vilalta et al., 2014). It has been found that the slope of the relationship between G_S and ln (D) is closely related to the magnitude of G_S at D = 1.0 kPa (G_Sref), and can be used as an empirical relationship to describe isohydric behavior (Oren et al., 1998). The stomatal sensitivity to D of isohydric plants is reported to be linearly proportional to G_Sref (i.e., -m = 0.6) (Pou et al., 2012), which provides insight into stomatal regulation. Some Eucalyptus (e.g., Eucalyptus gomphocephala) have been reported to allow a greater Ψ_L range than typical isohydric species and to occupy more drought-prone habitats, since they have xylem that is more resistant to negative water potentials (Franks et al., 2007; West et al., 2008). However, little is known about whether this behavior will facilitate the maximization of carbon assimilation for Eucalyptus.

Except for stomatal regulation, trees mainly respond to soil drought-induced water stress by changes to hydraulic properties, in order to adapt to the environment in the long term (Schäfer et al., 2000; Forrester, 2015). These changes are highly related to stomatal regulation. One of the most commonly observed strategies is that the hydraulic limitation of G_S by increasing path length can be mitigated by structural compensation, particularly a reduction in A_L/A_S (Becker et al., 2000; McDowell et al., 2002; Delzon et al., 2004). Some other compensating strategies have been observed, such as larger trees possessing deeper roots and larger conduit diameters (Mokany et al., 2003; Anderegg et al., 2012). Köstner et al. (2002) claimed that the increased path length and gravitational head concomitant with height (H) growth must be offset either by a reduction in G_S, the ratio of leaf area to sapwood area (A_L/A_S), Ψ_L, or by an increase in hydraulic conductivity (K_s), to maintain hydraulic balance for any given soil water potential (Ψs) and D. Eucalyptus species usually have large leaf area to support rapid stem growth (White et al., 1998), and thus have high transpiration demands at both the leaf and canopy levels during drought periods (Dawson, 1996). Therefore, we hypothesized that Eucalyptus are likely to maintain a constant G_s and support a higher A_L as trees grow in order to meet the great growth demands, while other strategies are employed to compensate for the increased hydraulic limitation with tree height and transpiration demand. To shed light on this aspect of Eucalyptus, it is necessary to quantify the effect of tree size on tree growth, as soil water decreases (Feichtinger et al., 2014).

Eucalyptus urophylla is the most widely planted forest tree in southern China and its area is still rapidly expanding (Shi et al., 2012). Our study is focused on how fast growing Eucalyptus forests in low subtropical China balance hydraulic safety and carbon assimilation under periodical drought. Specifically we asked: (1) How does this species coordinate decreased G_s with changes in hydraulic conductivity to maximize carbon assimilation in dry conditions? (2) How do stomatal regulation and hydraulic conductivity converge with tree structural changes so as to maintain fast growth?

Materials and Methods

Study Site and Plant Material

This study was conducted at the Huangmian state forest farm (24°66′N, 109°87′E), which is located approximately 60 km southwest of Guilin city in South China. This farm is planted with E. urophylla for lumber and pulp production. All of the measurements took place in a 3–5 year old E. urophylla stand on a hill with an inclination of approximately 30° facing southwest. The forest density was 1375 trees ha^-1. The soil of this forest is characterized as heavy loam. This area is characterized by a low subtropical monsoon climate with annual precipitation ranging from 1750 to 2000 mm and an average annual temperature of 19°C. Rainfall is unevenly distributed throughout the year, producing wet (March to September) and dry (October to February of the next year) seasons. Measurements were carried out from June 2012 to May 2013 on 15 trees. The mean tree height and diameter at breast height (DBH) of the sampled trees was 11.5 ± 2.9 m and 10.1 ± 2.2 cm, respectively. An instrument tower 23 m tall was set up within the plantation, providing access to the canopy of the forest stand.

Sap Flow and Environmental Factors

Self-made Granier-type sensors (20 mm in length; Granier et al., 1996) consisting of a heated (constant heat flow) probe and an unheated thermocouple probe were used to monitor the sap flow density (F_d, g m^-2 s^-1) of the sampled 15 trees. The probes were inserted into the xylem at breast height (1.3 m) on the north side of tree stems. The upper probe was supplied with a constant power of 120 mA. The temperature difference between both probes was measured and converted to F_d, according to Granier et al. (1996). More details of sensor installation have been described in Zhu et al. (2015) and Zhang et al. (2016). The F_d of E. urophylla is assumed to be isotropic in terms of evenly distributed leaf transpiration around the tree crown (Burgess and Dawson, 2008). F_d was used to estimate transpiration after it was converted into a spatially weighted mean flux based on the radial variation in sap flow density observed in another study of E. urophylla (n = 38, Zhou et al., 2004). They found that the variation in sapflow density from the outmost of the stem for 3–4 year old E. urophylla can be expressed as F_d = ax³+bx²+cx+d, where x is the ratio of the sensor depth to the radial sapwood thickness. We combined the results of the two plots in their study and obtained the equation F_d = 4.33x³-8.31x²+4.07x+0.52. Natural temperature gradients can lead to large potential errors of sap flow measurements (Do and Rocheteau, 2002), however, temperature gradients were found to be negligible in our study (Zhang et al., 2016).

A micro-meteorological station was built on the top of the tower. Photosynthetic photon flux density (Q₀, μmol m^-2 s^-1), temperature (T, °C), relative humidity (RH, %), and wind speed (u, m s^-1) were measured simultaneously with the sap flow measurements (Zhu et al., 2015; Zhang et al., 2016). Rainfall data (in Guilin) during the study period were obtained from the China Metrological Data Sharing Service System¹. Soil water content (SWC, m³ m^-3) was monitored with three soil water probes (SM300, UK) that were buried 30 cm under the ground surface.

Tree Morphological Features

For each sap flow tree, DBH was measured with a diameter tape, and tree height (h) was estimated with a tape dropped from the top of the tower. Leaf area (A_L) was estimated using an allometric relationship between DBH and the A_L that was constructed by harvesting seven trees outside (but near) the experimental plot. During the harvest, five small leaf sub-samples from each tree were scanned with a portable leaf area meter (LICOR-3000, USA) and weighed (fresh weight) to estimate specific leaf area (area/fresh mass ratio). Then all leaves of the harvested trees were collected, weighed and multiplied by the specific leaf area to obtain an estimate of whole tree A_L. The DBH of the harvested trees ranged from 6.6 to 11.1 cm, while those for sap flow trees ranged from 8.5 to 16.1 cm (i.e., the range of DBH for harvest trees didn’t cover the full range of trees used for sap flow measurements). Thus, we combined our DBH and A_L measurements with those from Zhu et al. (2009) (E. urophylla; n = 9) to derive an A_L – DBH relationship [A_L = 43.43^∗ (1-exp (-0.15DBH))^4.93, R² = 0.93, n = 16]. Data was obtained from the table in their paper. Sapwood depth and bark thickness were determined from stem cores (5 mm in diameter) obtained with an increment borer from selected trees outside the sap flux measurement plots (5 m away, in the same stand). The sapwood depth was visually distinguished from heartwood based on color, and was used to calculate sapwood area (A_s), which can be expressed as A_S = -0.008 + 0.0015DBH, R² = 0.97, n = 27. Since sample trees were estimated based on the relationship between DBH and A_s, we used the fitted relationship between DBH and A_s and the A_L from the harvested trees together to scale up whole tree transpiration (E_T). Nocturnal sap flux (E_T-NOC) was defined as E_T that occurred when Q₀ = 0. Since Eucalyptus are reported to have thick, tough and long lived leaves with weak seasonal dynamics (Reich et al., 1999), thus the variation in leaf area would not be accounted for these relationships.

Hydraulic Properties of Stem Xylem

The physical limitations on water transport in the xylem determine the stomatal behavior and transpiration in trees. This relationship is usually expressed as a combination of Darcy’s law with a simple expression for transpiration which is equated to liquid transport in wood (Whitehead and Jarvis, 1981):

${\mathrm{G}}_{\mathrm{S}\mathrm{r}\mathrm{e}\mathrm{f}}\mathrm{}\mathrm{\alpha }\mathrm{}{\mathrm{E}}_{\mathrm{L}}\mathrm{}\mathrm{=}{\mathrm{k}}_{\mathrm{s}}\mathrm{(}\mathrm{\Delta }\mathrm{\Psi }\mathrm{-}\mathrm{0.01}\mathrm{h}\mathrm{)}\frac{{\mathrm{A}}_{\mathrm{S}}}{{\mathrm{A}}_{{\mathrm{L}}^{\mathrm{h}}}}\mathrm{}\mathrm{\left(}\mathrm{1}\mathrm{\right)}$

Where k_s is the effective hydraulic conductivity from soil to leaves (whole-plant conductance per unit sapwood), and ΔΨ is the water potential difference between root and leaf.

In order to determine the wet-dry seasonal variation in ΔΨ, the leaf water potentials at pre-dawn (Ψ_pre-dawn, 5:00), pre-night (Ψ_pre-night, 19:00) and midday (Ψ_midday, 13:00) were measured with a portable pressure chamber (PMS 1000, Corvallis, OR, USA) on sunny days in the wet (5 days) and dry (4 days) seasons. Five trees were selected for measurement. Ψ_L were the mean of three replicate shoots with fully expanded leaves, sampled from the mid-crown of each tree. Since soil moisture variation within a single day is small, Ψ_pre-dawn was treated as a substitute for the water potential in the soil (Ψ_s) (Kim et al., 2008; Bleby et al., 2012). Thus, ΔΨ was estimated as the difference between Ψ_pre-dawn and Ψ_midday.

Canopy Stomatal Conductance

If forest transpiration is well-coupled with atmospheric factors, the mean stomatal conductance can be estimated based on a simplified equation (Köstner et al., 1992), which is derived from Whitehead and Jarvis (1981). Due to low LAI, the canopy was found to meet the assumptions necessary to adopt this equation (Zhu et al., 2015). It is assumed that the F_d-scaled transpiration combined with A_s/A_L is a proxy for transpiration rate per unit of leaf area (E_L). Therefore, mean stomatal conductance (G_s) for each tree, can be expressed as:

${\mathrm{G}}_{\mathrm{S}}\mathrm{=}\mathrm{\left(}{\mathrm{G}}_{\mathrm{V}}{\mathrm{T}}_{\mathrm{a}\mathrm{\rho }}{\mathrm{E}}_{\mathrm{L}}\mathrm{\right)}\mathrm{/}\mathrm{D}\mathrm{}\mathrm{\left(}\mathrm{2}\mathrm{\right)}$

where E_L is whole-tree transpiration per unit leaf area (g m^-2 s^-1), G_V is the universal gas constant adjusted for water vapor (0.462 m³kPa K^-1 kg^-1), T_a is the air temperature (K), ρ is the density of water (998 kg m^-3), and D is in kPa. G_Si is in units of mmol m^-2 s^-1 (Monteith and Unsworth, 2013).

The forest had an LAI of 1.68 ± 0.28 m² m^-2 and did not show significant seasonal changes (p = 0.78) (Zhu et al., 2015). Therefore, G_Si calculation is not subject to errors caused by leaf area dynamics. G_Si was estimated after (1) performing a cross-correlation analysis between D and F_d, and using the most appropriate time lag to implement a time-corrected F_d and (2) filtering out data where D < 0.6 kPa, in the hours of early morning and late afternoon (Oren et al., 1998).

Along with the Ψ_L measurements, we also measured leaf stomatal conductance (g_s) at mid-day on the abaxial surface of sun-exposed leaves with a steady-state porometer (SC-1, DECAGON, USA). Three leaves of each tree were chosen randomly for these measurements.

Stomatal Sensitivity to Vapor Pressure Deficit

Stomatal sensitivity is proportionally related to the magnitude of G_s at low D (D = 1 kPa) when soil moisture is not limiting (Granier et al., 1996), and it can be derived as:

${\mathrm{G}}_{\mathrm{S}}\mathrm{=}{\mathrm{G}}_{\mathrm{S}\mathrm{r}\mathrm{e}\mathrm{f}}\mathrm{-}\mathrm{m}\mathrm{}\ln \mathrm{D}\mathrm{}\mathrm{\left(}\mathrm{3}\mathrm{\right)}$

where G_Sref is the intercept (i.e., the value of G_s at D = 1 kPa in a log-linear relationship), and -m represents the slope of the regression fit representing stomatal sensitivity to D (i.e., dG_s/dln D). By analyzing data from a variety of sources, including both porometric and sap flux derived G_s, -m was demonstrated to be approximately 0.6 (Oren et al., 1998). In our study, the -m and G_Sref for E. urophylla in the wet and dry seasons was calculated to characterize the response of G_s to drought.

A boundary line analysis of the relationship between D and G_s was performed for the dry and wet seasons. The datasets of G_s for each tree were binned by radiation (nine levels from 0 to 1600 μmol m^-2 s^-1). The data at night (Q₀ = 0) were excluded because plant physiological response at night is much more complicated than that in the daytime (Oren et al., 2001). The relationship between the mean lnD and G_s of each subset was linearly fitted, and the intercept and slope corresponded to the G_Sref (G_s at D = 1 kPa) and sensitivity in response to D (dG_s/dlnD, mmol m^-2 s^-1 kPa^-1), respectively (Oren et al., 1998). Then, the relationship between G_Sref and -dlnd/dG_s for the two seasons was fitted.

In order to determine the radiation regulation of stomatal conductance under different water conditions, the G_Sref under different light conditions was normalized by the value of the maximum Q₀ of each tree in both seasons, and the relationship between the G_Sref and mean Q₀ at that level for all of the trees was fitted with an exponential function expressed as:

${\mathrm{G}}_{\mathrm{S}\mathrm{r}\mathrm{e}\mathrm{f}}\mathrm{=}\mathrm{a}\mathrm{\times }\mathrm{(}\mathrm{1}\mathrm{-}\exp \mathrm{}\mathrm{(}\mathrm{-}\mathrm{b}\mathrm{\times }{\mathit{Q}}_{\mathit{o}}\mathrm{)}\mathrm{)}\mathrm{.}\mathrm{}\mathrm{\left(}\mathrm{4}\mathrm{\right)}$

Where a refers to the maximum dependent variable, i.e., the max G_Sref (G_Sref-max).

Leaf Stable Carbon Isotopes

After the experiments, we randomly collected leaves at the top of the crown for 11 trees with DBH ranging from 5.2 to 20.4 cm near the sap flow measurement trees. Leaves were dried at 65°C to constant mass, and leaf dry mass was determined to the nearest mg. The dry leaves were then ground to a fine, homogeneous powder (Cernusak and Hutley, 2011). The leaf carbon isotope ratio was determined using a stable isotope ratio mass spectrometer (Isoprime 100, Isoprime, UK) on a subsample of approximately 3 mg leaf material. These analyses were performed in the Public Laboratory of South China Botanical Garden, Guangzhou, China. Carbon isotope discrimination (∆¹³C) in dry leaf matter was calculated as ∆¹³C = (δ¹³Ca - δ¹³Cp)/(1 + δ¹³Cp), where δ¹³Cp is δ¹³C of dry leaf matter, and δ¹³Ca is that of atmospheric CO₂. We assumed a value of -5.5‰ for δ¹³Ca, according to the previous measurements in low subtropical China (Zou et al., 2009).

Data Analysis

Boundary-line analysis was conducted in Excel (version 2010, Microsoft Office Excel) to set up the relationship between environmental conditions and maximum canopy stomatal conductance or F_d. The upper boundary line was derived by: (1) partitioning data of independent variables (V_I) into specific intervals, (2) calculating the mean and standard deviation of dependent variables (V_d) in each interval, (3) removing outliers (P < 0.05; Dixon’s test), (4) selecting the data falling above the mean plus one standard deviation, and (5) averaging the selected data for each V_I interval with n ≥ 5 remaining V_d values. The intervals with n < 5 was excluded to prevent V_I intervals with too little information from affecting the relationship.

Statistical analyses were performed using SAS (version 9.2, SAS Institute, Cary, NC, USA). A multiple regression analysis was conducted to determine the effect of hydraulic architecture on tree water use in the wet and dry seasons. A paired t-test was used to compare the differences in environmental and plant physiological responses between wet and dry seasons. Origin pro (version 8.6, Origin Lab, USA) was used to draw graphs.

Results

Water Conditions and Tree Water Use in Different Seasons

The precipitation (P) in the research site totaled 2167.6 mm from June 2012 to May 2013 (Figure 1). The water input was mainly contributed by precipitation in late spring and early summer (i.e., from April to June), which accounted for 55.4% of the annual total, while that from October to February (typical dry season in low subtropical China) was only 16%. The SWC in the dry season decreased 32.6% from the wet season, demonstrating a significant difference in the soil water conditions between the wet and dry seasons.

FIGURE 1

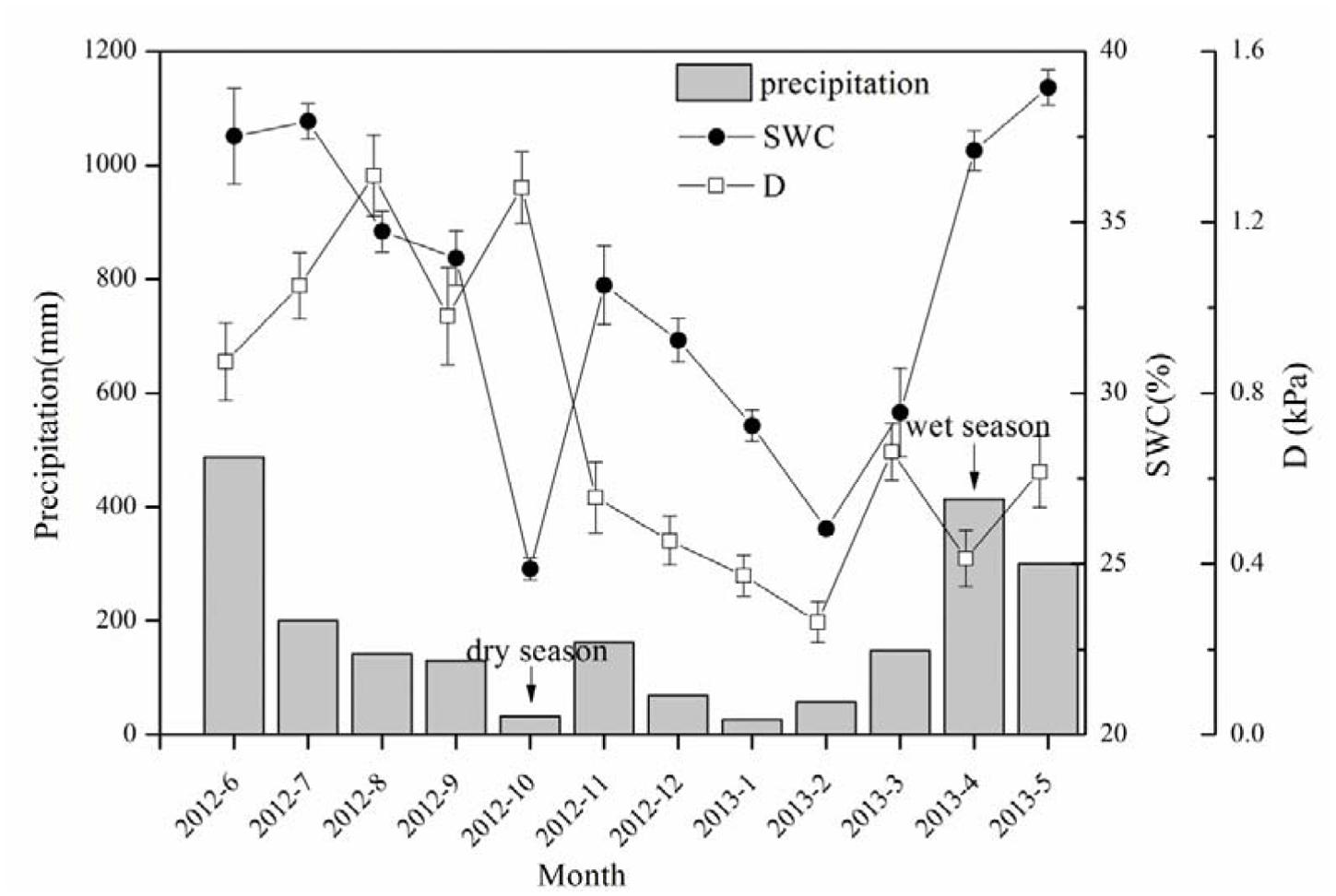
FIGURE 1. Precipitation (P), soil water content (SWC) and evaporative demand (D) during the period of sap flow measurement. SWC data shown in the figure are daily mean ± SE of that month, n = 28–31.

A boundary line analysis of the relationship between F_d and Q₀ was conducted, and the maximum F_d was derived from the exponential relationship. The mean F_d of the 15 trees was 41.03 ± 7.97 and 38.82 ± 13.16 g m^-2 s^-1 in the dry and wet seasons, respectively, consistent with the pattern of D (Figure 1). Overall, F_d was not affected by tree size, although it was weakly related to DBH in the dry season (R² = 0.19, p = 0.06). The wet/dry ratio of F_d varied from 0.4 to 0.8 and was not significantly related to the tree size (R² = 0.03). Average E_T in the dry season (5.7 ± 2.9 kg d^-1) was 58.0% higher than that in the wet season (3.6 ± 2.3 kg d^-1) (Figure 2A, p < 0.01), and linearly increased with tree size (p = 0.003). E_T-NOC was 0.18 ± 0.021 kg d^-1 in wet and 0.11 ± 0.01 kg d^-1 in dry seasons (Figure 2B, p = 0.047), which contributed 1.82 ± 0.45% and 4.51 ± 1.34% to daily E_T in dry and wet seasons, respectively. E_T-NOC was also linearly related with tree size (p < 0.01).

FIGURE 2

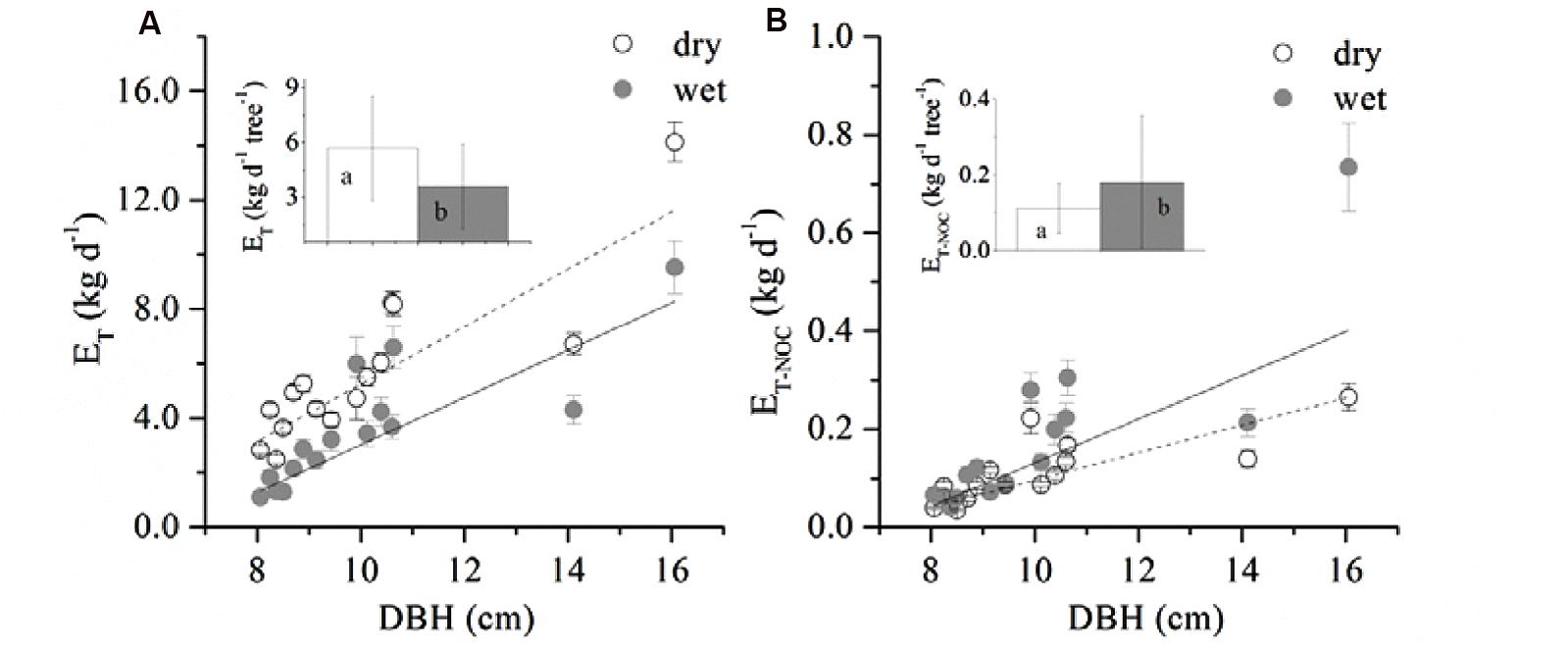
FIGURE 2. Relationship between DBH and (A) averaged daily transpiration (E_T), (B) averaged total nocturnal sap flow (E_T-NOC). Data are mean ± SE, and all linear fittings are significant at the p < 0.05 level. The insets in the figure represent the mean E_T (A) and E_T-NOC (B) of all 15 trees in dry and wet seasons respectively. Different letters indicate a significant difference between dry and wet seasons.

The average Ψ_pre-dawn and Ψ_pre-night was -0.24 ± 0.04 and -0.29 ± 0.02 MPa in the dry season and -0.21 ± 0.03 and -0.31 ± 0.05 MPa in the wet season. Seasonal differences for both were not significant (p > 0.05). The average Ψ_noon was higher (-0.75 ± 0.23 MPa) in the wet season than that in the dry season (-1.46 ± 0.23 MPa) (p < 0.01). Ψ_pre-dawn and Ψ_noon versus tree size in both seasons are shown in Figure 3. Tree size was not related to variations in either Ψ_pre-dawn and Ψ_noon. Accordingly, the water potential difference at midday (ΔΨ) had a mean of 0.62 ± 0.66 (wet) and 1.22 ± 0.10 MPa (dry). ΔΨ was much higher in wet than in dry season (p < 0.01). No difference existed among the five trees for the parameters above (p > 0.05).

FIGURE 3

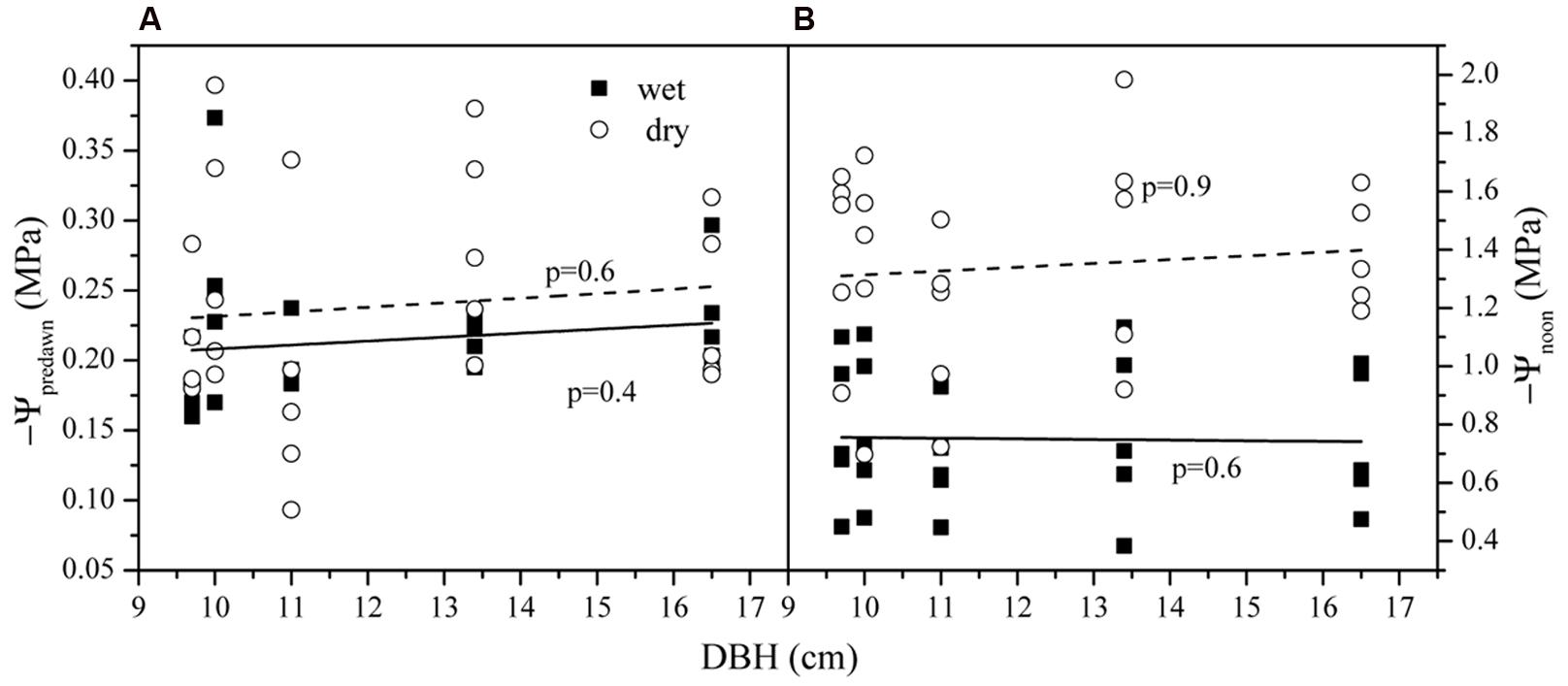
FIGURE 3. The leaf water potential at (A) pre-dawn (Ψ_pre-dawn) and (B) noon (Ψ_noon) along the tree size gradient in dry and wet seasons.

VPD Regulated G_s under Different Light Conditions

The time lag between D and G_s was found to be 1.3 and 0.5 h in dry and wet seasons respectively. Thus, time-lagged G_s was used to calculate G_Sref. G_Sref had a linear relationship with -dG_s/dLnD in both dry and wet seasons, but significant differences of the slopes were observed under different light levels (ANOVA, p < 0.01, Figure 4). Normalized G_Sref of all of the trees increased rapidly as Q₀ rose until maximum (Figure 5A). G_Sref reached 90% of the maximum (G_S90) when Q₀ was 287.8 and 167.1 μmol m^-2 s^-1 in the dry and wet seasons, respectively. This revealed that G_Sref was more sensitive to light in wet season, leading to a lower saturation point than that in the dry season (p < 0.01). It was found that -m at different light levels had a weak relationship with tree size (not shown; p = 0.33). The effect of Q₀ on –m was also quantified in both seasons (Figure 5B). –m gradually decreased with Q₀ before a short increase under low light conditions (ANOVA, Duncan, p < 0.01), i.e., the sensitivity was not constant within a single day when the light intensity varied substantially. When the data under low light conditions (Q₀< 200 μmol m^-2 s^-1) were removed, a linear decrease in -m ranging from 0.32 to 0.83 (dry season) and 0.22 to 1.10 (wet season) with radiation was observed for the 15 trees (Figure 5B). Mean -m was substantially higher in the wet season (0.58 ± 0.01) than in the dry season (0.53 ± 0.007) (p = 0.038).

FIGURE 4

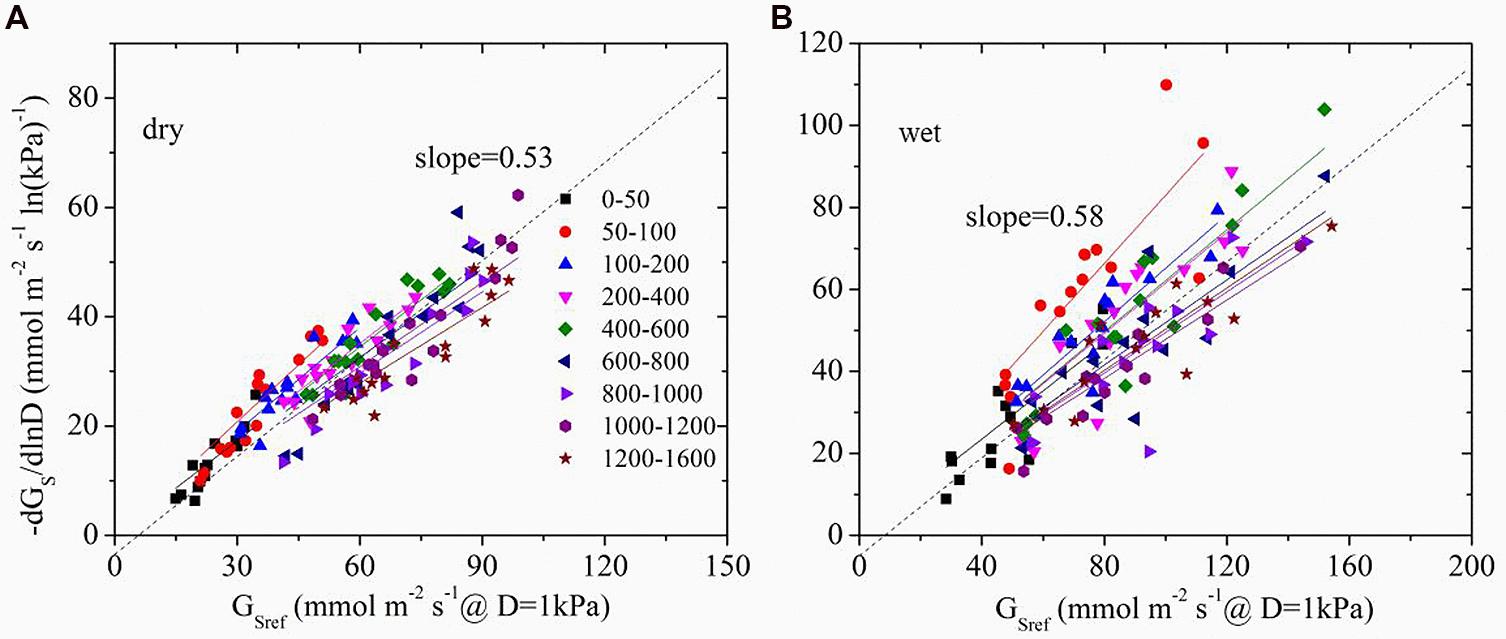
FIGURE 4. The sensitivity of average stomatal conductance of tree individuals at each light level in response to increasing vapor pressure deficit (-dG_s/dlnD) as a function of the canopy stomatal conductance at D = 1 kPa (G_Sref) in dry (A, October) and wet season (B, April). Different symbols represent the different light levels.

FIGURE 5

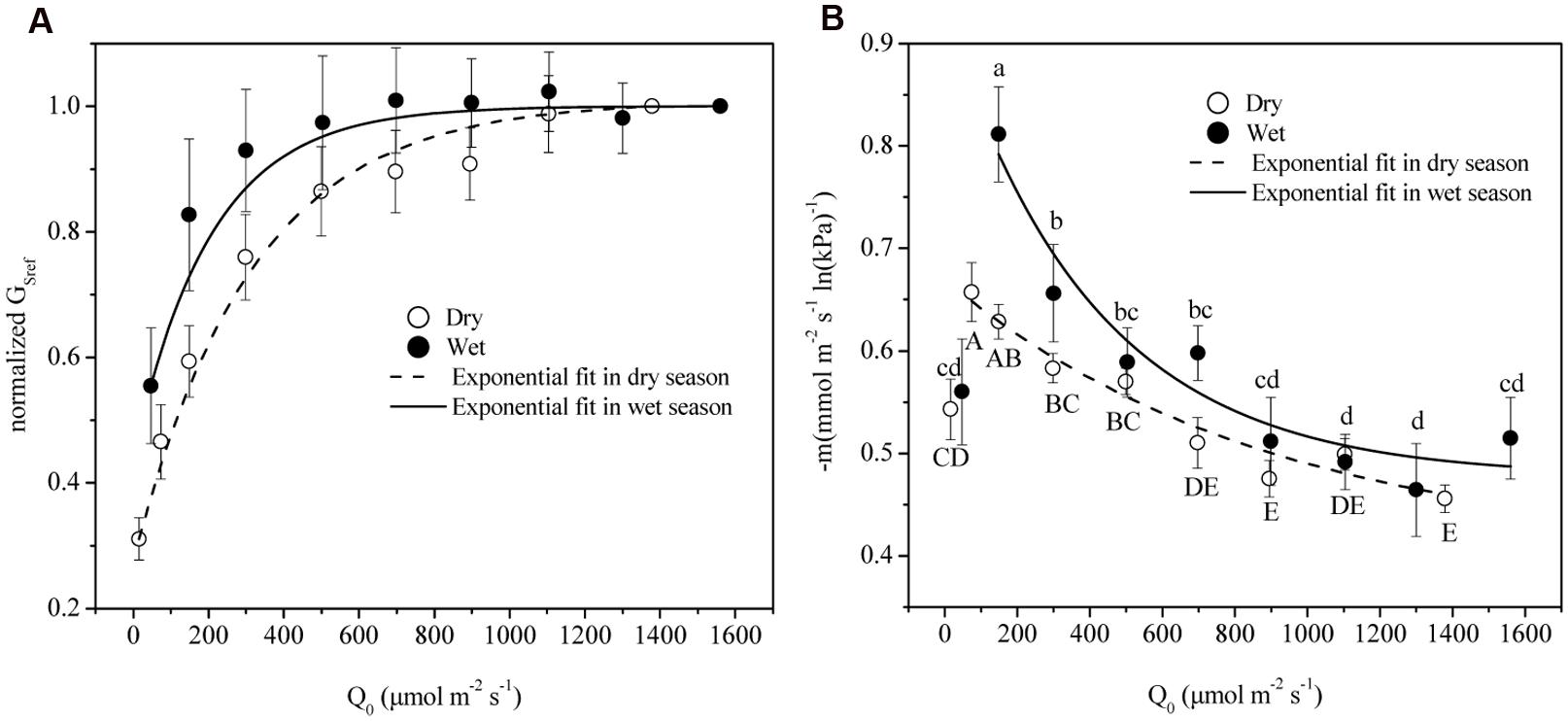
FIGURE 5. (A) G_Sref (G_s of each tree at D = 1 kPa) normalized based on the highest value in relation to mean photosynthetically active radiation (Q₀). (B) The stomatal sensitivity (–m) of each tree in relation to Q₀ in dry (open symbols) and wet seasons (solid symbols). Symbols are the mean ± SD of all 15 trees for each light group. Lines are least-square fit through the entire data. Symbols with same letters shown in (a) indicate non-significant differences among light groups, where capital/lower cases refer to dry/wet season.

Oren et al. (1998) reported that as long as stomata regulate the leaf potential near a constant value, a slope close to 0.6 is expected. The exact slope depends on the D range, boundary layer conductance (g_bl), and changes in hydraulic conductance associated with D. To determine the effect of the D range, boundary analysis was conducted with the data shown in Figure 4 when D = 1 kPa – 2 kPa for all light levels. -m derived from this range was compared with that from all of the data, and it turned out to be insignificantly different from the full range in both dry and wet seasons (p = 0.43 and 0.14, respectively, ANOVA). In addition, since E. urophylla has narrow leaves, g_bl in the stand during the wet and dry seasons was found to be 930.1 and 1149.8 mmol m^-2s^-1 (unpublished data), respectively, which led to a ratio of g_bl/G_s higher than 2 in the dry season. It is claimed that -m is negatively related to g_bl/G_s and equals 0.55 when the g_bl/G_s is 10 (Oren et al., 1998). Our lower value will produce a higher -m value (>0.55) in the dry season for E. urophylla. Thus, it is the changes in hydraulic conductance that are responsible for the -m variation.

Stomatal Regulation in Relation to Tree Size and Leaf Water Potential

We estimated the max G_s (G_Sref-max) of each tree from the exponential function (equation 4, corresponding to a) before it was normalized and fitted to DBH (Figure 6). G_Sref-max was found to increase with DBH in the wet season before reaching the maximum when DBH > 9 cm. While no clear relationship in the dry season was observed, the mean G_Sref-max was higher in the wet season (88.6 mmol m^-2 s^-1) than in the dry season (68.8 mmol m^-2 s^-1)(p < 0.01). The ratio of G_Sref-max in the dry to wet season ranged from 0.58 to 1.26 (0.81 on average), decreasing rapidly when DBH < 9 cm and stabilizing when DBH > 9 cm.

FIGURE 6

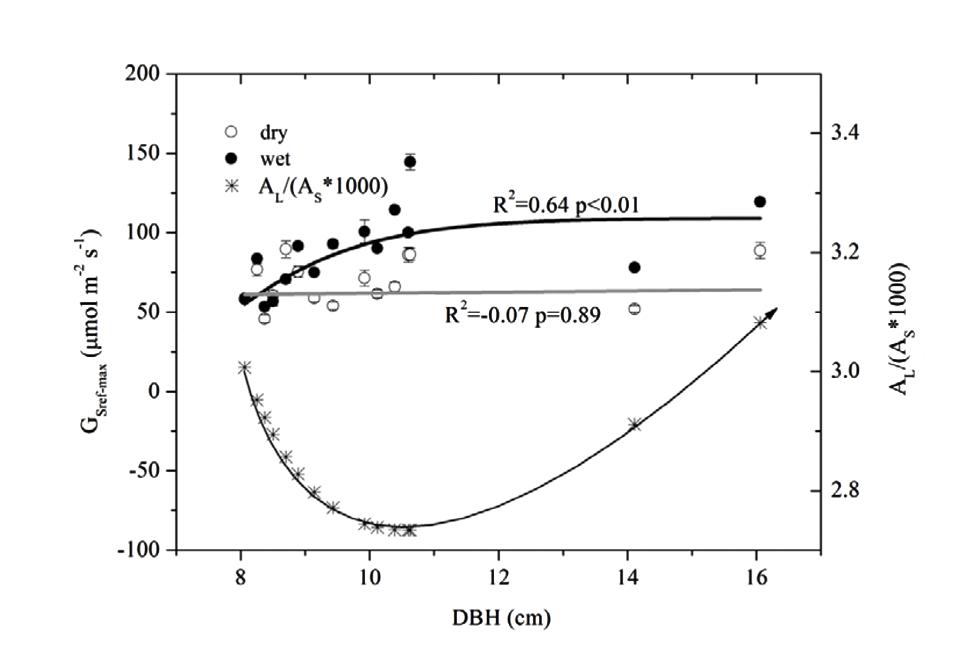
FIGURE 6. Relationship between DBH and maximum stomatal conductance at reference D (=1 kPa) (G_Sref-max) derived from Figure 4, and, the A_L/(A_s^∗1000) based on the predicted A_L and A_s with DBH. Lines represent least square fits for dry (white circle) and wet (black circle) seasons respectively; data are mean ± SE.

We also related Ψ_noon with the corresponding mid-day g_s (Figure 7A) and found a positive relationship between g_s and Ψ_L when light was low. Based on cell turgor theory, the change in Ψ_L is caused by the G_s-promoted water loss from the leaf (Dow and Bergmann, 2014). However, this value peaked and was maintained from -0.6 to -0.9 MPa before a gradual decrease.

FIGURE 7

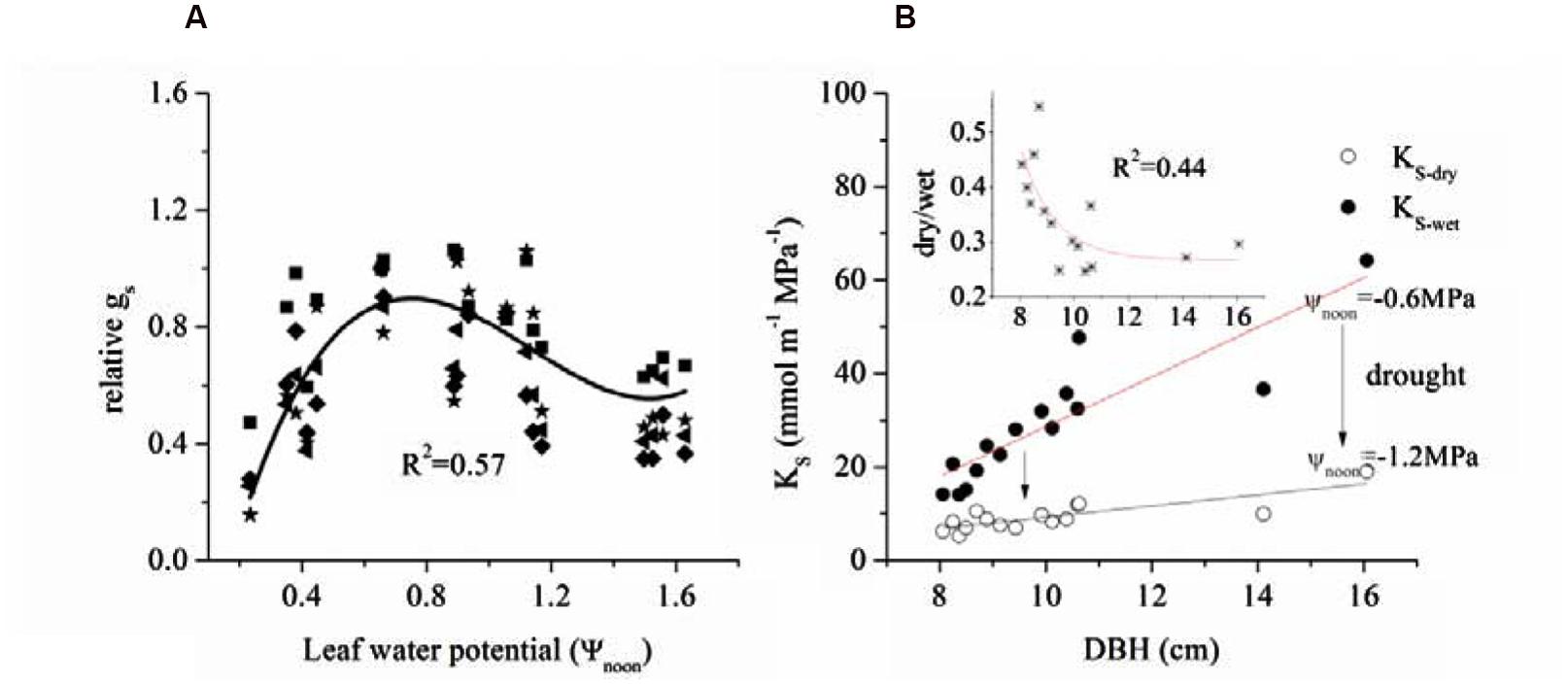
FIGURE 7. (A) Limitation of leaf water potential on relative g_s during mid-day (at noon, 12:00-13:00) and (B) relationship between tree size and specific hydraulic conductivity k_s of 15 sample trees in dry and wet seasons.

Hydraulic Conductivity

The combined effects of A_L/A_s, H and Ψ_L on stomatal conductance of the 15 trees were described using Equation (1) to quantify the tree hydraulic aspects of the plant physiological response (Table 1). The A_L/A_s gradually decreased up to approximately DBH = 10 cm, then started to increase when DBH > 11cm (Figure 6). We evaluated the seasonal change in k_s with Equation (1) when D = 1 kPa (Figure 7B). It was observed that k_s in the wet season was much higher than that in the dry season (29.1 ± 13.1 vs. 9.4 ± 3.2 mmol m^-1 MPa^-1). In addition, larger trees had a much higher seasonal variation in k_s (p < 0.01). As shown in Figure 7B, the dry to wet season ratio of k_s decreased rapidly with size growth, becoming constant for DBH > 10 cm.

TABLE 1

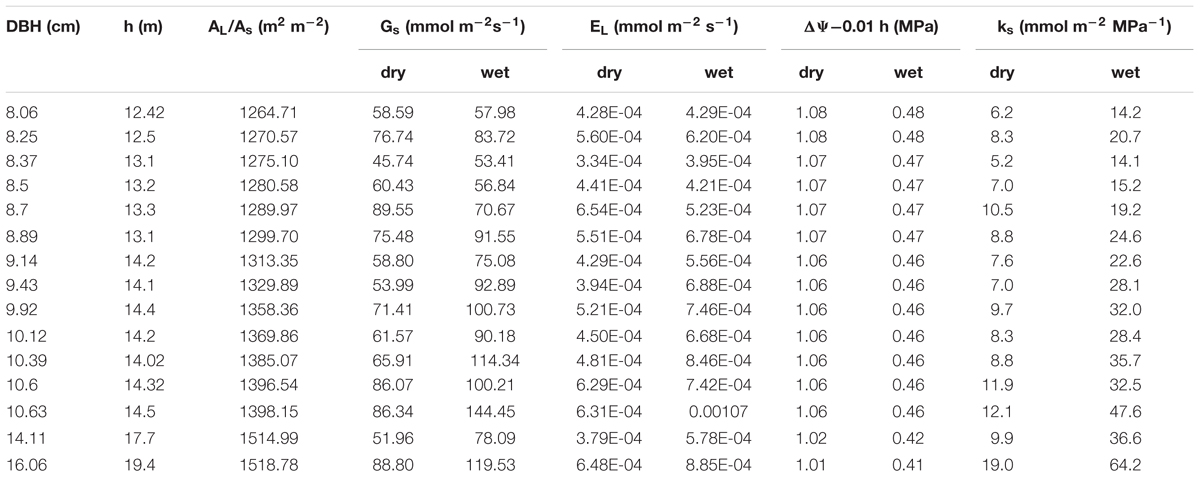
TABLE 1. Parameters that were employed to calculate k_s based on Equation 1 for each tree during the dry and wet seasons.

Discussion

Stomatal Regulation in Response to Leaf Water Potential

The mechanism of stomatal closure is viewed as a direct response to the change in leaf water potential that is related closely to cell turgor (Martorell et al., 2014). In this study, it appears that G_s was not held constant in order to maximize carbon assimilation for E. urophylla in dry conditions. We found that G_s decreased by 22.4% following a two-fold decrease in ΔΨ in the dry season (Figure 6). According to equation (2), we assumed that if G_s does not change, a 234.4% enhancement of E_L or E_T would be expected with increased D, since no significant difference in T_a and A_L was observed between the two seasons (p > 0.05). Thus, a 22.4% decrease in G_s eventually induced an increase in E_L or E_T of 159.5%.

That 50∼60% of maximum g_s was maintained at -1.6 MPa implies that E. urophylla was capable of optimizing carbon assimilation under stressed leaf water conditions. g_s peaked between -0.6 and -0.9 MPa after which it decreased gradually (Figure 6A), which is similar to the relationship between Ψ_L and g_s across 70 tree species including Eucalyptus (Klein, 2014). Another example reported by Mielke et al. (2000) showed that G_s of Eucalyptus grandis maintained ∼40% of the maximum when Ψ_L < -2.45 MPa before it reached the minimum Ψ_L (-2.8 MPa). It was observed that the stomata maintained 50–60% of the maximum G_s when Ψ_L reached the minimum (1.6 MPa) (Figure 7A), which was consistent with the stabilized G_s (∼37.5% of the maximum) when predawn Ψ_L < -2.37 for three allopatric Eucalyptus species (White et al., 2000). It was shown that the Ψ_L has a range of -2.2 MPa to -1.0 MPa when G_s decreased to 50% of the maximum for most tree species (Klein, 2014). Thus, it was claimed that the G_s of Eucalyptus species tended to be less sensitive to the decrease of ΔΨ than most other woody species. This had already been argued for Eucalyptus gomphocephala, since Ψ_L is not fixed at or above any particular value (co-varies with monthly rainfall) in a manner that is consistent with typical anisohydric behavior (Franks et al., 2007). Nevertheless, whether this behavior (i.e., not complete stomatal closure under low leaf water potentials) is general among all Eucalpytus or not needs further studies (Martorell et al., 2014).

We further quantified this anisohydric behavior via the variation of -m (Figure 5A). When light is limited, the increase of Q₀ will stimulate the opening of stomas as shown in Figure 4B, until the threshold is reached. Meanwhile, -m shared the same turning point of Q₀ with G_Sref before gradual decrease. Despite the stabilized G_Sref, the stomas became less sensitive to increased D as Q₀ increased, illustrated by the lower -m, i.e., anisohydric behavior. Thus, light plays a significant role in controlling the stomatal response to D and the carbon assimilation ability. Evidence has shown that taller trees with lower G_Sref sensitivity could maintain higher CO₂ uptake rates over the wide diurnal range of D, which serves to support carbon exchange (Schäfer et al., 2000). Evidently, it is the different perception ability of abscisic acid (ABA) that contributes to the plants isohydric or anisohydric behavior (Tardieu and Simonneau, 1998; Schultz, 2003; Sade et al., 2012), and the release of ABA tends to be activated only when pH is low (such as high Ci) (Ackerson, 1982). For species with higher photosynthetic capacity, lower Ci will be predicted under high light conditions, thus the higher G_s and the lower sensitivity to D.

Hydraulic Conductivity of E. urophylla

G_sref-max showed a decline of 22.5% from Ψ_L = -0.6 MPa to -1.2 MPa, which is less than the 45.3–65.6% decrease of k_s, implying a more important role of k_s regulation in restricting excessive transpiration. As we know, G_s as well as k_s coincide with decreased Ψ_L and start to decrease when xylem water refill cannot not balance canopy water loss (Franks et al., 2007). However, the extent of loss of hydraulic conductivity as Ψ_L decreases varies greatly across a variety of species, habitats, and climates (Hacke, 2014). Generally, species growing with high water supply tend to have larger vessels to promote a high hydraulic conductivity in the conducting tissue rather than to minimize the risk of drought-induced xylem embolism (Zach et al., 2010). In Eucalyptus grandis and the hybrid of Eucalyptus grandis × camaldulensis, vessel diameter and length increased from the dry to wet conditions as water uptake through transpiration increased (February et al., 1995). Because of high annual rainfall in our study site (2167.6 mm, Figure 1), growth of the xylem vessel of E. urophylla was found to have a mean diameter of 91.4 ± 10.1 μm (Zhao et al., 2014), which favors the significant decrease of k_s (45.3–65.6%) in dry conditions.

E_T was observed to increase significantly both in dry and wet season with tree size, which implied improved carbon assimilation (Kim et al., 2008). It was found that the changes of A_L/A_s didn’t follow consistent pattern as other studies have reported (increase or decrease, Figure 6) (Buckley and Roberts, 2006). However, the G_Sref-max in the wet season was observed to increase with tree size (Figure 6), and the increased tree height will lead to stomatal regulation (decreased g_s, Schäfer et al., 2000). Thus, the increased k_s with DBH (Figure 7B) was thought to contribute to the gradually increased E_T and G_s (Figure 2A and 6). In a tropical old-growth forest, for a variety of species, k_s was found to significantly increase with tree height because of the increased mean vessel diameter both in trunk and twig xylem (Zach et al., 2010). Finally, our results also revealed that there was no significant difference of Ψ_L among tree sizes (Figure 3). Bleby et al. (2012) reported that the decreased Ψ_L of Eucalyptus marginata usually occurred under natural conditions where resources were limited. At the same time, A_L/A_s was also found to decline in order to maintain hydraulic homeostasis. If the modification of Darcy’s Law for plant water translocation is correct, we can conclude that the increased burden on water transport due to increased G_s, A_L/A_s and tree height were well compensated by the increased k_s. However, increased k_s will lead to more vulnerable xylem in the face of drought stress (Thomas et al., 2004; Ladjal et al., 2005). As observed in Figure 7B, k_s decreased 45.3 and 65.6% respectively for the smallest and largest tree, which implies a lower resistance for suppressed trees with decreasing Ψ_L (Ambrose et al., 2009).

Enhanced WUE with Moderate Periodical Drought

The substantial increase of transpirational demand in the dry season led to the decrease of k_s and G_s (Figure 7B). We found that G_s decreased by 22.4% from the wet to dry seasons, while k_s decreased by 45.3–65.6% more than G_s. If leaves in both seasons have the same demand for CO₂, the WUE should be higher in the dry season. Such a water-use strategy may contribute to high water-use efficiency for E. urophylla, especially under dry conditions because water flux in the xylem is reduced more than G_s in the leaves. This possibility had been observed in some other studies (Brienen et al., 2011; Maseyk et al., 2011; Liu et al., 2012). In addition, the k_s ratio of dry/wet decreased from 0.55 to 0.30 with increased tree size (Figure 7B), implying a higher decrease in water loss for large trees. This meant that E. urophylla in our stands tended to improve their WUE in the dry period. To verify this hypothesis, we conducted leaf carbon isotope analysis along the tree size gradient. Consistently, Δ¹³C showed a clear decrease with DBH (Figure 8). A number of studies have argued that moderate drought favors high WUE of tree species from different ecosystems, including forest and desert (Maseyk et al., 2011; Liu et al., 2012). Otto et al. (2014) argued that dominant clonal Eucalyptus grandis × urophylla trees use water more efficiently compared with native species. However, the underlying mechanism responsible for higher WUE is unclear. Our results indicated possible mechanisms for high WUE in dominant trees, which might be verified by further studies on the annual net biomass yield/annual transpiration, since isotope discrimination only provides an estimate of intrinsic WUE rather than the ratio of uptaken CO₂ to actual fluxes of water vapor.

FIGURE 8

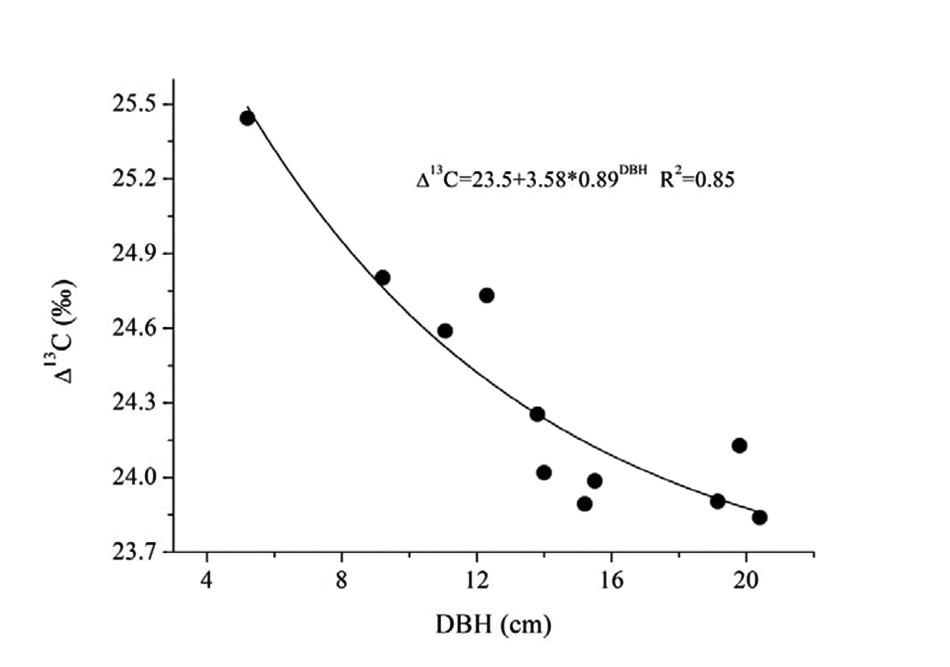
FIGURE 8. Relationship between DBH and the leaf carbon isotope discrimination (¹³C) of 11 trees for E. urophylla.

Conclusion

In a moist low subtropical area in South China with periodic drought, E. urophylla was observed to close stomata under lower water supply conditions with decreased Ψ_L, but showed anisohydric behavior with gradually stabilizing high G_s at low Ψ_L, especially under high light conditions (deceased -m). k_s decreased 45.3–65.6% from wet to dry season, which is significantly higher than the proportional decline of G_s (22.4%) and may be responsible for the high WUE of Eucalyptus species. As tree size increased, greater sensitivity of k_s to water loss was synchronous with improved WUE (decreased Δ¹³C), which contributed to the constant stomatal conductance in the dry season (G_Sref-max) and the persistent increase of A_L/A_s with DBH and insignificant change in Ψ_L among trees for maintaining the hydraulic balance. We are uncertain of the generality of the above behavior for other Eucalyptus species, which deserves further studies.

Author’s Note

We declare that the previous version of this manuscript “Water use strategies of a young Eucalyptus urophylla forest in response to seasonal change of climatic factors in South China” submitted to Biogeosciences Discussion (doi: 10.5194/bgd-12-10469-2015) and appearing as a preprint service, was finally rejected.

Author Contributions

ZZ and PZ organized and supported the entire study. HM, LO, JN, LZ, GN, and YH performed the sap flow and physiological measurements. ZZ also wrote this manuscript, PZ and HM edited this manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was supported by the National Nature Science Foundation of China (Grant No. 41630752, 41030638, 41275169), and the CAS/SAFEA International Partnership Program for Creative Research Teams, Guangxi Key Sci & Tech Foundation (GuiKeZhong 1347001). We thank Prof. Ram Oren for his substantial advice and comments on the writing of this manuscript. We are indebted to Dr. Syed Ashraful Alam, who worked both at South China Botanical Garden/CAS and Department of Physics of the University of Helsinki, for his comments and efforts to improve the language of the manuscript. Data used in this study were collected by the author and are available from the author upon request.

Footnotes

1. ^http://data.cma.cn/

References

Ackerson, R. C. (1982). Synthesis and movement of abscisic acid in water-stressed cotton leaves. Plant Physiol. 69, 609–613. doi: 10.1104/pp.69.3.609

CrossRef Full Text | Google Scholar

Ambrose, A. R., Sillett, S. C., and Dawson, T. E. (2009). Effects of tree height on branch hydraulics, leaf structure and gas exchange in California redwoods. Plant Cell Environ. 32, 743–757. doi: 10.1111/j.1365-3040.2009.01950.x

CrossRef Full Text | Google Scholar

Anderegg, W. R. L., Berry, J. A., Smith, D. D., Sperry, J. S., Anderegg, L. D. L., and Field, C. B. (2012). The roles of hydraulic and carbon stress in a widespread climate-induced forest die-off. Proc. Natl. Acad. Sci. U.S.A. 109, 233–237. doi: 10.1073/pnas.1107891109

CrossRef Full Text | Google Scholar

Becker, P., Meinzer, F. C., and Wullschleger, S. D. (2000). Hydraulic limitation of tree height: a critique. Funct. Ecol. 14, 4–11. doi: 10.1046/j.1365-2435.2000.00397.x

CrossRef Full Text | Google Scholar

Bleby, T. M., Colquhoun, I. J., and Adams, M. A. (2012). Hydraulic traits and water use of Eucalyptus on restored versus natural sites in a seasonally dry forest in southwestern Australia. For. Ecol. Manage. 274, 58–66. doi: 10.1016/j.foreco.2012.02.029

CrossRef Full Text | Google Scholar

Brienen, R. J. W., Wanek, W., and Hietz, P. (2011). Stable carbon isotopes in tree rings indicate improved water use efficiency and drought responses of a tropical dry forest tree species. Trees 25, 103–113. doi: 10.1007/s00468-010-0474-1

CrossRef Full Text | Google Scholar

Buckley, T. N., and Roberts, D. W. (2006). How should leaf area, sapwood area and stomatal conductance vary with tree height to maximize growth? Tree Physiol. 26, 145–157. doi: 10.1093/treephys/26.2.145

CrossRef Full Text | Google Scholar

Burgess, S. S. O., and Dawson, T. E. (2008). Using branch and basal trunk sap flow measurements to estimate whole-plant water capacitance: a caution. Plant Soil 305, 5–13. doi: 10.1007/s11104-007-9378-2

CrossRef Full Text | Google Scholar

Cernusak, L. A., and Hutley, L. B. (2011). Stable isotopes reveal the contribution of corticular photosynthesis to growth in branches of Eucalyptus miniata. Plant Physiol. 155, 515–523. doi: 10.1104/pp.110.163337

CrossRef Full Text | Google Scholar

Chaves, M. M., Pereira, J. S., Maroco, J., Rodrigues, M. L., Ricardo, C. P. P., Osorio, M. L., et al. (2002). How plants cope with water stress in the field. photosynthesis and growth. Ann. Bot. 89, 907–916. doi: 10.1093/aob/mcf105

CrossRef Full Text | Google Scholar

Davidson, E. A., de Araújo, A. C., Artaxo, P., Balch, J. K., Foster Brown, I., Bustamante, M. M. C., et al. (2012). The amazon basin in transition. Nature 481, 321–328. doi: 10.1038/nature10717

CrossRef Full Text | Google Scholar

Dawson, T. E. (1996). Determining water use by trees and forests from isotopic, energy balance and transpiration analyses: the roles of tree size and hydraulic lift. Tree Physiol. 16, 263–272. doi: 10.1093/treephys/16.1-2.263

CrossRef Full Text | Google Scholar

Delzon, S., Sartore, M., Burlett, R., Dewar, R., and Loustau, D. (2004). Hydraulic responses to height growth in maritime pine trees. Plant Cell Environ. 27, 1077–1087. doi: 10.1111/gcb.13148

CrossRef Full Text | Google Scholar

Do, F., and Rocheteau, A. (2002). Influence of natural temperature gradients on measurements of xylem sap flow with thermal dissipation probes, 1. Field observations and possible remedies. Tree Physiol. 22, 641–648. doi: 10.1093/treephys/22.9.641

CrossRef Full Text | Google Scholar

Dow, G. J., and Bergmann, D. C. (2014). Patterning and processes: how stomatal development defines physiological potential. Curr. Opin. Plant Biol. 21, 67–74. doi: 10.1016/j.pbi.2014.06.007

CrossRef Full Text | Google Scholar

February, E. C., Stock, W. D., Bond, W. J., and Leroux, D. J. (1995). Relationships between water availability and selected vessel characteristics in Eucalyptus grandis and two hybrids. Iawa J. 16, 269–276. doi: 10.1163/22941932-90001410

CrossRef Full Text | Google Scholar

Feichtinger, L. M., Eilmann, B., Buchmann, N., and Rigling, A. (2014). Growth adjustments of conifers to drought and to century-long irrigation. For. Ecol. Manage. 334, 96–105. doi: 10.1016/j.foreco.2014.08.008

CrossRef Full Text | Google Scholar

Forrester, D. I. (2015). Transpiration and water-use efficiency in mixed-species forests versus monocultures: effects of tree size, stand density and season. Tree Physiol. 35, 289–304. doi: 10.1093/treephys/tpv011

CrossRef Full Text | Google Scholar

Franks, P. J., Drake, P. L., and Froend, R. H. (2007). Anisohydric but isohydrodynamic: seasonally constant plant water potential gradient explained by a stomatal control mechanism incorporating variable plant hydraulic conductance. Plant Cell Environ. 30, 19–30. doi: 10.1111/j.1365-3040.2006.01600.x

CrossRef Full Text | Google Scholar

Granier, A., Biron, P., Kostner, B., Gay, L. W., and Najjar, G. (1996). Comparisons of xylem sap flow and water vapour flux at the stand level and derivation of canopy conductance for Scots pine. Theor. Appl. Climatol. 53, 115–122. doi: 10.1007/BF00866416

CrossRef Full Text | Google Scholar

Hacke, U. G. (2014). Variable plant hydraulic conductance. Tree Physiol. 34, 105–108. doi: 10.1093/treephys/tpu007

CrossRef Full Text | Google Scholar

Hölttä, T., Mencuccini, M., and Nikinmaa, E. (2011). A carbon cost-gain model explains the observed patterns of xylem safety and efficiency. Plant Cell Environ. 34, 1819–1834. doi: 10.1111/j.1365-3040.2011.02377.x

CrossRef Full Text | Google Scholar

Jones, H. G. (1998). Stomatal control of photosynthesis and transpiration. J. Exp. Bot. 49, 387–398. doi: 10.1093/jexbot/49.suppl_1.387

CrossRef Full Text | Google Scholar

Kim, H.-S., Oren, R., and Hinckley, T. M. (2008). Actual and potential transpiration and carbon assimilation in an irrigated poplar plantation. Tree Physiol. 28, 559–577. doi: 10.1093/treephys/28.4.559

CrossRef Full Text | Google Scholar

Klein, T. (2014). The variability of stomatal sensitivity to leaf water potential across tree species indicates a continuum between isohydric and anisohydric behaviours. Funct. Ecol. 28, 1313–1320. doi: 10.1111/1365-2435.12289

CrossRef Full Text | Google Scholar

Köstner, B., Falge, E., and Tenhunen, J. D. (2002). Age-related effects on leaf area/sapwood area relationships, canopy transpiration and carbon gain of Norway spruce stands (Picea abies) in the Fichtelgebirge, Germany. Tree Physiol. 22, 567–574. doi: 10.1093/treephys/22.8.567

CrossRef Full Text | Google Scholar

Köstner, B. M. M., Schulze, E. D., Kelliher, F. M., Hollinger, D. Y., Byers, J. N., Hunt, J. E., et al. (1992). Transpiration and canopy conductance in a pristine broad-leaved forest of Nothofagus: an analysis of xylem sap flow and eddy correlation measurements. Oecologia 91, 350–359. doi: 10.1007/BF00317623

CrossRef Full Text | Google Scholar

Ladjal, M., Huc, R., and Ducrey, M. (2005). Drought effects on hydraulic conductivity and xylem vulnerability to embolism in diverse species and provenances of Mediterranean cedars. Tree Physiol. 25, 1109–1117. doi: 10.1093/treephys/25.9.1109

CrossRef Full Text | Google Scholar

Liu, R., Pan, L.-P., Jenerette, G. D., Wang, Q.-X., Cieraad, E., and Li, Y. (2012). High efficiency in water use and carbon gain in a wet year for a desert halophyte community. Agric. For. Meteorol. 162, 127–135. doi: 10.1016/j.agrformet.2012.04.015

CrossRef Full Text | Google Scholar

Lloret, F., Escudero, A., Maria Iriondo, J., Martinez-Vilalta, J., and Valladares, F. (2012). Extreme climatic events and vegetation: the role of stabilizing processes. Glob. Change Biol. 18, 797–805. doi: 10.1111/j.1365-2486.2011.02624.x

CrossRef Full Text | Google Scholar

Martínez-Vilalta, J., Poyatos, R., Aguadé, D., Retana, J., and Mencuccini, M. (2014). A new look at water transport regulation in plants. New Phytol. 204, 105–115. doi: 10.1111/nph.12912

CrossRef Full Text | Google Scholar

Martorell, S., Diaz-Espejo, A., Medrano, H., Ball, M. C., and Choat, B. (2014). Rapid hydraulic recovery in Eucalyptus pauciflora after drought: linkages between stem hydraulics and leaf gas exchange. Plant Cell Environ. 37, 617–626. doi: 10.1111/pce.12182

CrossRef Full Text | Google Scholar

Maseyk, K., Hemming, D., Angert, A., Leavitt, S. W., and Yakir, D. (2011). Increase in water-use efficiency and underlying processes in pine forests across a precipitation gradient in the dry Mediterranean region over the past 30 years. Oecologia 167, 578–585. doi: 10.1007/s00442-011-2010-4

CrossRef Full Text | Google Scholar

McDowell, N. G., Phillips, N., Lunch, C., Bond, B. J., and Ryan, M. G. (2002). An investigation of hydraulic limitation and compensation in large, old Douglas-fir trees. Tree Physiol. 22, 763–774. doi: 10.1093/treephys/22.11.763

CrossRef Full Text | Google Scholar

Meinzer, F. C. (1993). Stomatal control of transpiration. Trends Ecol. Evol. 8, 289–294. doi: 10.1016/0169-5347(93)90257-P

CrossRef Full Text | Google Scholar

Mielke, M. S., Oliva, M. A., de Barros, N. F., Penchel, R. M., Martinez, C. A., da Fonseca, S., et al. (2000). Leaf gas exchange in a clonal eucalypt plantation as related to soil moisture, leaf water potential and microclimate variables. Trees Struct. Funct. 14, 263–270. doi: 10.1007/s004680050012

CrossRef Full Text | Google Scholar

Mokany, K., McMurtrie, R. E., Atwell, B. J., and Keith, H. (2003). Interaction between sapwood and foliage area in alpine ash (Eucalyptus delegatensis) trees of different heights. Tree Physiol. 23, 949–957. doi: 10.1093/treephys/23.14.949

CrossRef Full Text | Google Scholar

Monteith, J., and Unsworth, M. (2013). Principles of Environmental Physics: Plants, Animals, and the Atmosphere. New York: Academic Press.

Google Scholar

Oren, R., Phillips, N., Katul, G., Ewers, B. E., and Pataki, D. E. (1998). Scaling xylem sap flux and soil water balance and calculating variance: a method for partitioning water flux in forests. Ann. For. Sci. 55, 191–216. doi: 10.1051/forest:19980112

CrossRef Full Text | Google Scholar

Oren, R., Sperry, J. S., Ewers, B. E., Pataki, D. E., Phillips, N., and Megonigal, J. P. (2001). Sensitivity of mean canopy stomatal conductance to vapor pressure deficit in a flooded Taxodium distichum L. forest: hydraulic and non-hydraulic effects. Oecologia 126, 21–29. doi: 10.1007/s004420000497

CrossRef Full Text | Google Scholar

Otto, M. S. G., Hubbard, R. M., Binkley, D., and Stape, J. L. (2014). Dominant clonal Eucalyptus grandis× urophylla trees use water more efficiently. For. Ecol. Manage. 328, 117–121. doi: 10.1016/j.foreco.2014.05.032

CrossRef Full Text | Google Scholar

Pou, A., Medrano, H., Tomàs, M., Martorell, S., Ribas-Carbó, M., and Flexas, J. (2012). Anisohydric behaviour in grapevines results in better performance under moderate water stress and recovery than isohydric behaviour. Plant Soil 359, 335–349. doi: 10.1007/s11104-012-1206-7

CrossRef Full Text | Google Scholar

Reich, P. B., Ellsworth, D. S., Walters, M. B., Vose, J. M., Gresham, C., Volin, J. C., et al. (1999). Generality of leaf trait relationships: a test across six biomes. Ecology 80, 1955–1969. doi: 10.1890/0012-9658(1999)080[1955:GOLTRA]2.0.CO;2

CrossRef Full Text | Google Scholar

Rosen, R. (2013). Optimality Principles in Biology. Berlin: Springer.

Google Scholar

Ryan, M. G., and Waring, R. H. (1992). Maintenance respiration and stand development in a subalpine lodgepole pine forest. Ecology 73, 2100–2108. doi: 10.2307/1941458

CrossRef Full Text | Google Scholar

Sade, N., Gebremedhin, A., and Moshelion, M. (2012). Risk-taking plants: anisohydric behavior as a stress-resistance trait. Plant Signal. Behav. 7, 767–770. doi: 10.4161/psb.20505

CrossRef Full Text | Google Scholar

Schäfer, K. V. R., Oren, R., and Tenhunen, J. D. (2000). The effect of tree height on crown level stomatal conductance. Plant Cell Environ. 23, 365–375. doi: 10.1046/j.1365-3040.2000.00553.x

CrossRef Full Text | Google Scholar

Schultz, H. R. (2003). Differences in hydraulic architecture account for near-isohydric and anisohydric behaviour of two field-grown Vitis vinifera L. cultivars during drought. Plant Cell Environ. 26, 1393–1405. doi: 10.1046/j.1365-3040.2003.01064.x

CrossRef Full Text | Google Scholar

Shi, Z., Xu, D., Yang, X., Jia, Z., Guo, H., and Zhang, N. (2012). Ecohydrological impacts of eucalypt plantations: a review. J. Food Agric. Environ. 10, 1419–1426.

Google Scholar

Tardieu, F., and Simonneau, T. (1998). Variability among species of stomatal control under fluctuating soil water status and evaporative demand: modelling isohydric and anisohydric behaviours. J. Exp. Bot. 49, 419–432. doi: 10.1093/jxb/49.Special_Issue.419

CrossRef Full Text | Google Scholar

Thomas, D. S., Montagu, K. D., and Conroy, J. P. (2004). Changes in wood density of Eucalyptus camaldulensis due to temperature - the physiological link between water viscosity and wood anatomy. For. Ecol. Manag. 193, 157–165. doi: 10.1016/j.foreco.2004.01.028

CrossRef Full Text | Google Scholar

West, A. G., Hultine, K. R., Sperry, J. S., Bush, S. E., and Ehleringer, J. R. (2008). Transpiration and hydraulic strategies in a pinon-juniper woodland. Ecol. Appl. 18, 911–927. doi: 10.1890/06-2094.1

CrossRef Full Text | Google Scholar

White, D., Beadle, C., Worledge, D., Honeysett, J., and Cherry, M. (1998). The influence of drought on the relationship between leaf and conducting sapwood area in Eucalyptus globulus and Eucalyptus nitens. Trees 12, 414–414. doi: 10.1007/s004680050167

CrossRef Full Text | Google Scholar

White, D. A., Turner, N. C., and Galbraith, J. H. (2000). Leaf water relations and stomatal behavior of four allopatric Eucalyptus species planted in Mediterranean southwestern Australia. Tree Physiol. 20, 1157–1165. doi: 10.1093/treephys/20.17.1157

CrossRef Full Text | Google Scholar

Whitehead, D., and Beadle, C. L. (2004). Physiological regulation of productivity and water use in Eucalyptus: a review. For. Ecol. Manag. 193, 113–140. doi: 10.1016/j.foreco.2004.01.026

CrossRef Full Text | Google Scholar

Whitehead, D., and Jarvis, P. (1981). “Coniferous forests and plantations,” in ‘Water Deficits and Plant Growth’, ed. T. T. Kozlowski (New York: Academic Press), 49–152.

Google Scholar

Zach, A., Schuldt, B., Brix, S., Horna, V., Culmsee, H., and Leuschner, C. (2010). Vessel diameter and xylem hydraulic conductivity increase with tree height in tropical rainforest trees in Sulawesi, Indonesia. Flora 205, 506–512. doi: 10.1093/treephys/tps122

CrossRef Full Text | Google Scholar

Zhai, P. M., Zhang, X. B., Wan, H., and Pan, X. H. (2005). Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 18, 1096–1108. doi: 10.1175/JCLI-3318.1

CrossRef Full Text | Google Scholar

Zhang, Z. Z., Zhao, P., McCarthy, H. R., Zhao, X. H., Niu, J. F., Zhu, L. W., et al. (2016). Influence of the decoupling degree on the estimation of canopy stomatal conductance for two broadleaf tree species. Agric. For. Meteorol. 221, 230–241. doi: 10.1016/j.agrformet.2016.02.018

CrossRef Full Text | Google Scholar

Zhao, P. Q., Zhao, P., Niu, J. F., Zhu, L. W., Ni, G. Y., Gao, J. G., et al. (2014). Relationship between vessel characteristics and sap flow of eight subtropical tree species. J. Trop. Subtrop. Bot. 22, 537–548.

Zhou, G., Peng, C., Li, Y., Liu, S., Zhang, Q., Tang, X., et al. (2013). A climate change-induced threat to the ecological resilience of a subtropical monsoon evergreen broad-leaved forest in Southern China. Glob. Change Biol. 19, 1197–1210. doi: 10.1111/gcb.12128

CrossRef Full Text | Google Scholar

Zhou, G., Wei, X. H., Wu, Y. P., Liu, S. G., Huang, Y., Yan, J., et al. (2011). Quantifying the hydrological responses to climate change in an intact forested small watershed in Southern China. Glob. Change Biol. 17, 3736–3746. doi: 10.1111/j.1365-2486.2011.02499.x

CrossRef Full Text | Google Scholar

Zhou, G. Y., Yin, G. C., Morris, J., Bai, J. Y., Chen, S. X., Chu, G. W., et al. (2004). Measured sap flow and estimated evapotranspiration of tropical Eucalyptus urophylla plantations in south China. Acta Bot. Sin. 46, 202–210.

Google Scholar

Zhu, H. G., Yang, Y. Q., Wen, Y. G., Liang, H. W., and Yang, Y. Q. (2009). Estimating model for leaf area of standing tree and stand of E. grandis× E. urophylla in in Guangxi. J. Anhui Agric. Sci. 37, 15069–15070.

Zhu, L. W., Zhao, P., Wang, Q., Ni, G. Y., Niu, J. F., Zhao, X. H., et al. (2015). Stomatal and hydraulic conductance and water use in a eucalypt plantation in Guangxi, southern China. Agric. For. Meteorol. 202, 61–68. doi: 10.1016/j.agrformet.2014.12.003

CrossRef Full Text | Google Scholar

Zou, L., Sun, G., Zhao, P., Cai, X. A., Zeng, X., and Liu, X. (2009). Carbon isotope discrimination in leaf juice of Acacia mangium and its relationship to water-use efficiency. Front. For. China 4, 201–207. doi: 10.1007/s11461-009-0027-1

CrossRef Full Text | Google Scholar