Connecting Biochemical Photosynthesis Models with Crop Models to Support Crop Improvement

The next advance in field crop productivity will likely need to come from improving crop use efficiency of resources (e.g., light, water, and nitrogen), aspects of which are closely linked with overall crop photosynthetic efficiency. Progress in genetic manipulation of photosynthesis is confounded by uncertainties of consequences at crop level because of difficulties connecting across scales. Crop growth and development simulation models that integrate across biological levels of organization and use a gene-to-phenotype modeling approach may present a way forward. There has been a long history of development of crop models capable of simulating dynamics of crop physiological attributes. Many crop models incorporate canopy photosynthesis (source) as a key driver for crop growth, while others derive crop growth from the balance between source- and sink-limitations. Modeling leaf photosynthesis has progressed from empirical modeling via light response curves to a more mechanistic basis, having clearer links to the underlying biochemical processes of photosynthesis. Cross-scale modeling that connects models at the biochemical and crop levels and utilizes developments in upscaling leaf-level models to canopy models has the potential to bridge the gap between photosynthetic manipulation at the biochemical level and its consequences on crop productivity. Here we review approaches to this emerging cross-scale modeling framework and reinforce the need for connections across levels of modeling. Further, we propose strategies for connecting biochemical models of photosynthesis into the cross-scale modeling framework to support crop improvement through photosynthetic manipulation.

Introduction

Global crop production needs to approximately double by 2050 to meet the projected demands from rising population, diet shifts, and increasing needs for biofuels. Current trends in yield improvement of major field crops (i.e., wheat, rice, maize, and soybean), however, are insufficient to meet the projected demand (Ray et al., 2013; Fischer et al., 2014). In addition, more frequent extreme weather conditions associated with climate change are likely to have negative impacts on global crop yields (Lobell and Gourdji, 2012). Yield improvement in the past 50 years has been achieved through improved genetics via conventional plant breeding coupled with enhanced agronomy and crop protection (e.g., maize in the US; Duvick, 2005). Crop yield can be viewed as the product of resource capture (e.g., light, water, and nitrogen), the efficiency with which these resources are converted into biomass, and the extent of partitioning of biomass to harvestable product (i.e., harvest index). Yield improvement to date has been largely associated with improved efficiency to capture resources and with harvest index (Tollenaar and Lee, 2006; Fischer, 2007). While opportunities remain for improving grain yield through improved resource capture (e.g., root architecture Singh et al., 2012) and biomass partitioning (Duvick, 2005; Messina et al., 2009), these traits may be approaching their biological limits (Duvick and Cassman, 1999; Long et al., 2015). The one area in which there is little evidence of improvement is in crop use efficiency of resources, aspects of which depend on overall crop photosynthetic efficiency. While there is evidence of genetic variation in resource use efficiency (Henderson et al., 1998; Hammer et al., 2010), causal links to yield improvement are limited (Fischer et al., 1998; Sadras and Lawson, 2011).

Enhancing photosynthesis is becoming one focus for pursuing greater crop use efficiency of resources (Long et al., 2006; Zhu et al., 2010). This is made possible by: (1) our understanding of the photosynthetic pathway, (2) emergence of high-performance computing for simulating photosynthetic processes across scales from photosynthetic biochemistry to crop level, and (3) advances in genetic engineering (Long et al., 2015). There is now a well-defined agenda for the genetic manipulation of the biochemical pathway of photosynthesis at the leaf level for crop yield improvement (see review of Evans, 2013). Examples include engineering the C₄ photosynthetic pathway into rice (http://c4rice.irri.org/) and improving leaf CO₂ capture efficiency and light energy capture efficiency (http://photosynthesis.org.au). However, manipulation of photosynthesis at the biochemical level may not necessarily correlate with crop yield (see reviews of Sinclair et al., 2004; Long et al., 2006). This is because the gap between the biochemical and crop level of biological organizations confounds crop improvement (Sinclair et al., 2004; Hammer et al., 2006). Integrating to crop level is complicated by the (photosynthetic) genetic controls, dynamics of crop growth and development and their interactions with the environment.

There is a need to close the gap between the biochemical and crop levels using modeling to help accelerate progress in photosynthesis enhancement for crop improvement. A cross-scale modeling approach connecting these two levels with each other and with environmental effects provides a valuable theoretical framework for closing this gap. Crop level growth and development dynamics and effects of environments can be simulated with crop models that incorporate both source- and sink-limited crop growth (Hammer et al., 2010; Gent and Seginer, 2012; Fatichi et al., 2014). Nonetheless, canopy photosynthesis is a key driver in crop models. Photosynthesis models, focused at different levels of modeling, have evolved from empirical modeling of the photosynthetic light response (Blackman, 1905) to upscaling to the canopy level (Monsi and Saeki, 1953), and to connections with crop models (e.g., de Wit et al., 1978). At the crop level, canopy Radiation Use Efficiency (RUE) has been used successfully to determine the sum of photosynthetic output of individual leaves in the canopy (Monteith and Moss, 1977; Sinclair and Muchow, 1999) and RUE underpins crop growth prediction in many crop models (Parent and Tardieu, 2014). This simple approach avoids the need to connect photosynthesis between biochemical and canopy levels, although theoretical derivations have shown the clear connection of RUE with leaf photosynthesis within crop canopies (Hammer and Wright, 1994). These empirical canopy photosynthesis modeling approaches have been useful, but lack the biological functionality to capture canopy level consequences of genetic modification of photosynthesis at the biochemical level attributed to their aggregated nature. Biochemical models of photosynthesis, based on key biochemical processes of photosynthesis, have been developed at the leaf level (Farquhar et al., 1980; von Caemmerer and Farquhar, 1981; Farquhar and von Caemmerer, 1982; von Caemmerer and Furbank, 1999; von Caemmerer, 2000). These more mechanistic biochemical photosynthesis modeling approaches have been useful in interpreting gas exchange measurements of steady-state CO₂ assimilation of leaves and in predicting responses of leaf photosynthesis to genetic and environmental controls of photosynthesis and have been subsequently upscaled to the canopy level (Sellers et al., 1992; Leuning et al., 1995; de Pury and Farquhar, 1997). However, the biochemical models, by their intrinsic instantaneous nature, lack the integrative ability to capture interactions with key aspects of crop growth and development dynamics throughout the crop life cycle. Cross-scale modeling that connects across scales of biological organization and utilizes model developments in both photosynthesis and crop growth and development dynamics provides a means to capture the dynamics of photosynthesis manipulation to support crop improvement. In this review we pursue three objectives to aid the development of cross-scale modeling. These are to:

1. Summarize the emerging cross-scale modeling framework for connecting photosynthesis models at canopy and biochemical levels (Figure 1);

2. Identify avenues to improve connections in the cross-scale modeling framework with effects of environmental factors and crop physiological attributes;

3. Propose strategies for connecting biochemical photosynthesis models into the cross-scale modeling framework.

FIGURE 1

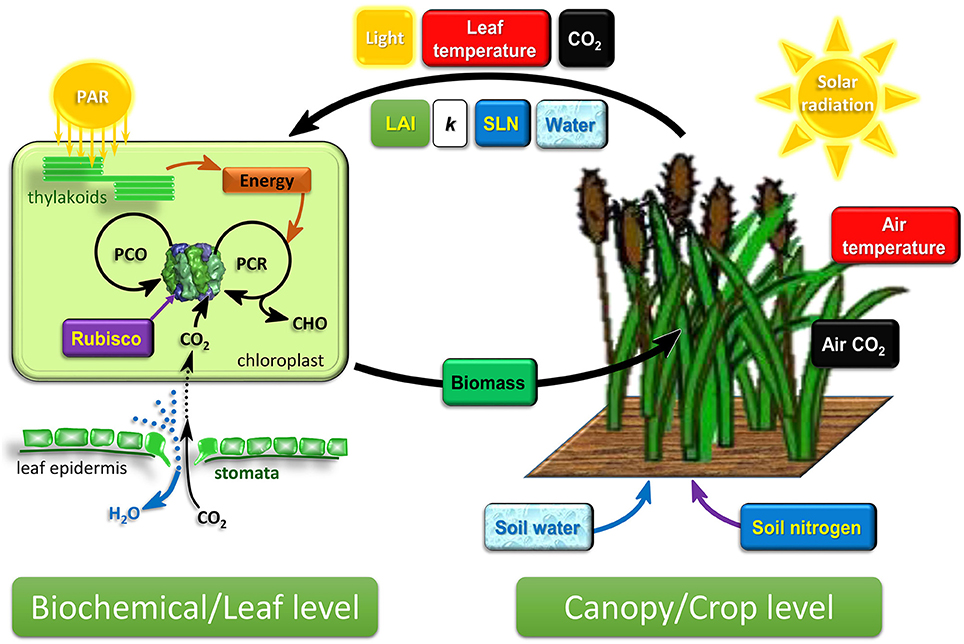
Figure 1. Schematic diagram of the emerging cross-scale modeling framework connecting biochemical/leaf-level photosynthesis and canopy/crop-level growth and development dynamics. Crop growth and development is driven by the development of canopy leaf area and canopy biomass growth, both of which are influenced by the prevailing environment and the photosynthesis output of individual leaves in the canopy. The canopy captures resources from the environment. Leaf photosynthesis is driven by the attributes of the crop canopy and leaves. LAI, SLN, and crop water status are determined by crop scale growth and development dynamics, while light, leaf temperature, and CO₂ experienced by leaves are influenced by canopy attributes, LAI and k. This two-way connection between biochemical and crop level (the two thick arrows) is an important consideration in the cross-scale modeling framework. PAR, photosynthetic active radiation; LAI, leaf area index; k, canopy light extinction coefficient; SLN, specific leaf nitrogen; PCR, photosynthetic carbon reduction cycle; PCO, photorespiratory carbon oxidation cycle; CHO, carbohydrates synthesized by photosynthesis.

Cross-Scale Modeling Framework for Connecting Photosynthesis Models at Canopy and Biochemical Levels

In crop models, canopy photosynthesis is a key driver of crop growth (de Wit, 1965; Duncan et al., 1967; Goudriaan and van laar, 1978; Thornley, 2002; El-Sharkawy, 2011). Early canopy photosynthesis modeling involved either (i) integrating photosynthesis of individual leaves in the canopy (de Wit, 1965; Duncan et al., 1967; Goudriaan and van laar, 1978), or (ii) utilizing the simple linear relationship observed between accumulated crop canopy biomass and intercepted solar radiation (Shibles and Weber, 1965, 1966; Williams et al., 1965; Monteith and Moss, 1977), also known as RUE (g/MJ) (Sinclair and Muchow, 1999). Depending on the details required for simulating canopy photosynthesis, either type of model can be used to drive growth in crop models. For example, crop models such as GECROS (Yin and van Laar, 2005) use the first approach, while APSIM (Holzworth et al., 2014) and DSSAT (Jones et al., 2003) use the second approach, although APSIM does have the provision to switch between the two approaches by incorporating an optional module with leaf photosynthesis light response curves and canopy architecture algorithms (Hammer et al., 2009).

Leaf Photosynthesis Light Response Modeling

Radiation (or light) intensity (I) is the key environmental factor for photosynthesis. Hence, the explicit modeling of the response of leaf photosynthesis (A) to I, or the A/I curve, has been a key focus since the beginning of leaf photosynthesis modeling. Modeling of leaf A/I curves, referred to as photosynthetic light-response (PLR) modeling, has a long history. Blackman (1905) describes a response of photosynthesis to light that increases linearly with I with a slope α (maximum quantum yield) until the maximum rate of photosynthesis (A_max), where CO₂ supply becomes limiting (Table 1). α is the maximum efficiency with which light can be converted to chemical energy by photosynthesis (assimilated CO₂ per quantum of absorbed light). It is known to be similar across a wide range of C₃ species when expressed on the basis of absorbed light (Ogren, 1993) and does not depend on either irradiance or leaf nitrogen content per unit leaf area (Thornley, 1998). The two parts of the photosynthesis light response curve are described as light- and CO₂-limited, respectively. This approach is plausible, but is restricted by the sharp discontinuity at the transition between the two limiting factors.

TABLE 1

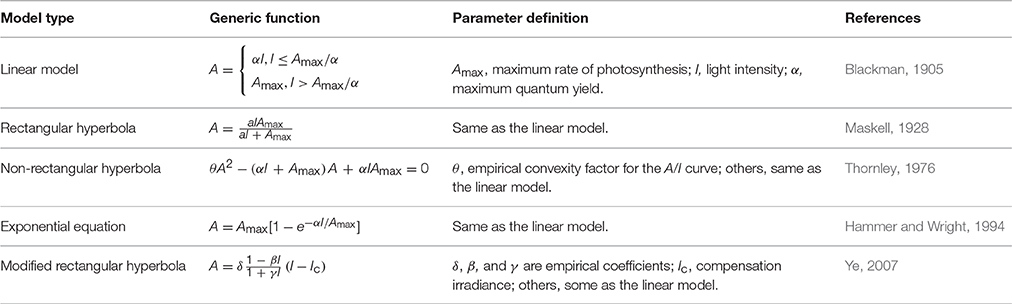
Table 1. List of major photosynthetic light-response models of leaf photosynthesis (A) response to light intensity (I).

To overcome this issue, responses using rectangular hyperbola type functions (Table 1) were developed (Maskell, 1928). This type of function, based on Michaelis and Menten's equation, reproduces the curvilinear trend of A/I curves. However, it poorly describes A/I curves at saturating levels of CO₂ and overestimates A_max, α and dark respiration (R_d), because the limitation on photosynthesis of the physical diffusion of CO₂ from the atmosphere to the site of carboxylation in leaves has not been taken into account (Akhkha, 2010).

Rabinowitch (1951) combined a simplified description of biochemical reactions of photosynthesis and the physical diffusion of CO₂ and generated the non-rectangular hyperbola type function (Table 1). Modeling of A/I curve using this function type has since been pursued by many authors with numerous variations (Ogren, 1993; Thornley, 1998, 2002; Xu et al., 2014). In addition to A_max and α, the non-rectangular hyperbola type function has an additional parameter θ (the curvature factor), which governs the “convexity” of the A/I curve. Ogren (1993) concluded that the A/I curve is usually truncated at the transition from electron-transport limitation to a limitation by ribulose-1,5-bisphosphate carboxylase-oxygenase (Rubisco); the convexity changes with CO₂ levels as the transition shifts, with respect to I, in the A/I curve. Marshall and Biscoe (1980) subsequently extended the function to include R_d. The rectangular hyperbola function is a special case of the non-rectangular hyperbola function (Thornley, 1998). Exponential functions (Table 1) have also been used to model A/I curves of C₃ and C₄ species based on experimental observations (Hammer and Wright, 1994).

Ye (2007) developed a modified rectangular hyperbola function with empirical coefficients (Table 1), which has improved fit to A/I curves of Oryza sativa. The derivative of the modified rectangular hyperbola (at I = 0) gives the maximum quantum yield. In subsequent work, Ye et al. (2013) developed a mechanistic A/I model based on the modified rectangular hyperbola function and ascribed the then empirical coefficients to light-harvesting characteristics and associated biophysical parameters of photosynthetic pigment molecule—mechanisms that underpin photosynthetic electron transport via photosystem II. This model is applicable for both C₃ and C₄ species, and demonstrated excellent levels of correspondence with observed responses (Ye et al., 2013).

Besides the key environmental factor of light, physiological attributes of the plants have significant effects on photosynthesis (Evans, 1989; Sinclair and Horie, 1989). Hence, their incorporation in PLR models is important. The PLR models have also evolved to incorporate improved connections between model parameters and crop physiological attributes that influence photosynthesis. For example, A_max, a parameter present in almost all PLR models, has been related to leaf nitrogen content per unit leaf area, which is commonly referred to as specific leaf nitrogen (SLN) (Muchow and Sinclair, 1994). Use of advanced PLR models with links between model parameters and crop physiological attributes will contribute to improving accuracy and connections in the cross-scale modeling.

Canopy Light Distribution Modeling

In the crop production environment, incident solar radiation is dynamic and can be described with solar geometry models and atmospheric transmissivity coefficients (Campbell, 1977; Brock, 1981; Hammer and Wright, 1994; Monteith and Unsworth, 2013a). At the earth's surface, solar radiation can be separated into direct and diffuse components, with the latter due to scattering of light as it travels through the atmosphere. Both components of incident light are important for canopy photosynthesis (de Wit, 1959, 1965; Duncan et al., 1967) and have become an essential part of canopy photosynthesis modeling (Duncan et al., 1967; Hammer and Wright, 1994; de Pury and Farquhar, 1997).

The complexity of canopy photosynthesis was first described by Boysen Jensen (1932), who demonstrated that canopy photosynthesis light response differs from that of isolated leaves in the canopy (Hirose, 2005). It differs because leaves in a canopy are exposed to different light environments throughout the day, depending on their spatial arrangement (e.g., leaf position in the canopy and leaf angle), the solar radiation intensity, and the location of the sun as it crosses the sky on its diurnal and seasonal course. In general, top leaf layers in the canopy receive more direct and intense light, while lower leaf layers receive much less light due to shading, although some direct light penetrates even to the lowest layer. This heterogeneity in radiation is a main factor complicating canopy photosynthesis.

Monsi and Saeki (1953) were among the first to quantify how sunlight is diminished as it proceeds into a canopy and is intercepted by leaves. They developed the first canopy light distribution model to characterize the light environment in a canopy. This model can be classified as a 1D canopy model, where the light environment only varies vertically in canopies and is assumed homogenous in the horizontal plane. Monsi and Saeki (1953) showed that light attenuation is approximately exponential in canopies and can thus be modeled by the common form of the Beer-Lambert equation for light extinction in homogenous media (in the context of a canopy):

$\begin{array}{ll}I=I_0{e}^{-k*LAI}& (1)\end{array}$

where LAI is the cumulative leaf area index from the top of the canopy above the layer of interest, I is the light intensity received at the layer of interest, I₀ is the light intensity at the top of the canopy, and k is the light extinction coefficient. Equation (1) has been applied in many crop models that apply a static value of k for the canopy as spatial arrangement of leaves can be assumed homogeneous throughout the growing season. This simplification has led to wide adoption of Monsi and Saeki's approach in subsequent canopy photosynthesis modeling (Monsi and Saeki, 1953; Saeki, 1960; de Wit, 1965; Duncan et al., 1967) and it remained important for canopy light distribution modeling in later work (Sinclair et al., 1976; Hammer and Wright, 1994; Leuning et al., 1995; de Pury and Farquhar, 1997). Estimates of diurnal photosynthesis and growth of field crops using the 1D formalisms applied over a diverse range of environments have shown this approach to be effective and robust (Hammer and Wright, 1994; Hammer et al., 2009).

Canopy light distribution modeling has subsequently been expanded to include more detailed canopy models. Multi-layer models (de Wit, 1965; Monteith, 1965b; Duncan et al., 1967; Goudriaan, 1977) were developed by dividing the canopy into layers that are specified by their respective LAI. For each layer, LAI can be divided into sunlit and shaded leaf fractions and the sunlit fraction can be further divided into leaf angle classes (Duncan et al., 1967; Sinclair et al., 1976). The intensity of solar radiation reaching each fraction is calculated using the Beer-Lambert equation (Equation 1). The shaded fraction is assumed to intercept diffuse solar radiation and radiation reflected and transmitted through canopy layers. The sunlit fraction is assumed to intercept direct solar radiation in addition to the three types of radiation intercepted by the shaded fraction (Duncan et al., 1967; Leuning et al., 1995; de Pury and Farquhar, 1997). Later canopy models (e.g., Leuning et al., 1995; de Pury and Farquhar, 1997) have incorporated details about attenuation of different types of radiation through the use of different k-values. Simpler approximations for the multiple leaf angle classes, such as the three leaf-angle classes treatment (Goudriaan, 1988), or the spherical leaf angle distribution (de Wit et al., 1978), can be assumed to avoid the need for parameterizing leaf angles in the canopy. The spherical leaf angle distribution is a simple and robust approach for canopy photosynthesis and crop RUE modeling that has been widely implemented in later canopy photosynthesis models (Goudriaan, 1977; Hammer and Wright, 1994; Leuning et al., 1995; de Pury and Farquhar, 1997). Further, the multi-layer feature can be eliminated by integrating the canopy across LAI for both sunlit and shaded leaf fractions. This results in a simpler representation of the canopy that retains the distinction between sunlit and shaded leaf fractions, a necessity for capturing heterogeneous radiation in canopies. It has been shown that simulations using this single layer sun-shade modeling approach agree very closely with those using the multi-layer modeling approach in predicting canopy photosynthesis (de Pury and Farquhar, 1997) and agreed (within 5%) with results using a static 3D plant architecture model (Roupsard et al., 2008). This validates the robustness of the sun-shade modeling approach.

However, there is evidence that variation in k can have significant effects on crop growth. k can be influenced by developmental stage, canopy configurations (Evers et al., 2009) and canopy architectural traits, such as leaf shape, leaf angle, and internode length (Hirose, 2005; Kahlen et al., 2008). This requires a more dynamic k than used in Equation (1). Duncan et al. (1967) developed a model of k as a function of canopy average leaf angle and sun angle that could predict seasonal maize dry matter production with high accuracy (r = 0.94). Hammer et al. (2009) applied this approach in their modeling work and found that canopy-average leaf angle would only have significant effect on maize grain yield under very high yielding situations [well-watered and high (>6 plants/m²) planting density]. k has also been modeled empirically with respect to canopy LAI (Tahiri et al., 2006). The APSIM wheat model has the provision to specify k in terms of crop row spacing. Modeling of k has progressed from assuming a static value to connection with crop canopy attributes.

Despite its effectiveness and robustness, it can be argued that the 1D modeling approaches are limited in their ability to explicitly describe effects of canopy architectural traits on canopy light distribution. Emergence of 3D plant architecture models may overcome this limitation (Vos et al., 2010). This includes the RATP model (Sinoquet et al., 2001), which has the capacity to simulate the spatial distribution of light interception in an isolated tree crown using a static 3D canopy architecture model and a 3D extension of the Beer-Lambert equation (Equation 1). Further, Chen et al. (2014) developed a detailed 3D canopy architecture model for a tomato crop, which allows simulation of its growth and its effects on the canopy light distribution and absorption. The derived k using this model is significantly affected by leaf angle and internode length; k is higher during the early growth period (<30 days after first leaf appearance in this case), but stabilizes at a lower value for the remainder of crop growth. In this case, the early growth period contributed to less than 10% of the final shoot dry mass. Because biomass accumulation of field crops during these early developmental stages is generally only a small proportion of the biomass accumulated at maturity, the simpler 1D modeling approach, where k is assumed static throughout crop development, is generally effective and robust. However, the drawback is that it is more difficult to predict canopy light distribution if architectural traits (Song et al., 2013; Chen et al., 2014) or planting configuration (Evers et al., 2009) are manipulated. This is where the 3D approach may have some advantages.

Connecting Photosynthetic Light-Response Models to Canopy Light Distribution

One of the early approaches for modeling of canopy photosynthesis was based on combining the development in PLR models with the simplified canopy models for canopy light distribution calculation (de Wit, 1965; Duncan et al., 1967; Goudriaan and van laar, 1978). However, incorporation of this approach into crop models quickly illustrated that aspects of canopy photosynthesis are influenced by crop growth and development dynamics and vice versa. For example, many crop models generate canopy LAI over the crop growing season; this influences the amount of solar radiation intercepted by crop canopy, which in turn influences canopy photosynthesis and drives crop growth (Figure 1). The same basic modeling precept has been applied in more detailed canopy architectural models (Vos et al., 2010). Instead of using a simplified description of canopy structure (such as k and canopy LAI), those models explicitly describe the development of the 3D canopy architecture of plants (e.g., Chen et al., 2014). This can be coupled with Monte Carlo ray tracing for canopy light absorption calculation, which can be used to drive PLR models (Vos et al., 2010). Consideration of the two-way connection between the PLR models [which have advanced to become more accurate (Section Leaf Photosynthesis Light Response Modeling)] with canopy light distribution provides a foundation for canopy photosynthesis modeling in the cross-scale modeling framework.

Utilizing Relationships between Crop Growth and Light Interception

One of the first attempts to describe crop productivity, as opposed to leaf photosynthesis, as a function of radiation appeared in the work of de Wit (1959) and Loomis and Williams (1963). Many authors have since reported linear relationships between dry mass production and intercepted solar radiation for various species. The landmark paper by Monteith and Moss (1977) consolidated the grounds for this relationship both experimentally and theoretically (Sinclair and Muchow, 1999), and led to the term RUE. Calculation of canopy biomass growth with the RUE approach is achieved simply by multiplying solar radiation intercepted by the canopy (e.g., Equation 1), based on the canopy light distribution model (Monsi and Saeki, 1953), with a pre-determined RUE (Sinclair and Muchow, 1999). Although the RUE approach brings empiricism to the canopy level, as opposed to the leaf level with the PLR models, its simplicity and practicality facilitated its widespread adoption in crop modeling to quantify crop growth.

One of the first uses of the RUE approach in crop models appeared in Sinclair (1986) and it continues to have a significant role in more recent crop modeling advances (e.g., Hammer et al., 2010). The RUE is species dependent and is usually higher in C₄ species than C₃ species. Based on a total solar radiation basis (which is approximately double the photosynthetic active radiation), the RUE of maize under optimal growing conditions is 1.6–1.7 g/MJ, but can be as high as 1.9 g/MJ (Lindquist et al., 2005). Similarly, the RUE of pearl millet, which is another C₄ species, is in the vicinity of 2.0 g/MJ (van Oosterom et al., 2002). For the C₄ species sorghum, the RUE of 3-dwarf germplasm is generally only 1.2–1.4 g/MJ (Sinclair and Muchow, 1999), although a tall, 1-dwarf Indian hybrid had a RUE in the range of 1.6–1.8 g/MJ (Hammer et al., 2010), similar to maize and pearl millet. In contrast, for C₃ species, the RUE of wheat is ~1.2 g/MJ, whereas soybean, which is a dicotyledonous legume crop with a different leaf structure, has a RUE of ~1 g/MJ (Sinclair and Muchow, 1999).

The RUE increases with the nitrogen status of the leaves, particularly if leaf N is limiting growth (Sinclair and Horie, 1989). For C₄ crops maize and sorghum, RUE increases rapidly from a SLN level of 0.3 g/m² and approaches a plateau when SLN reaches its critical value of ca. 1 g/m² (Muchow and Sinclair, 1994), beyond which any increase in SLN has no significant effect on crop growth. For C₃, rice the minimum SLN was similar to maize and wheat (0.3 g/m²), but the critical SLN was around 2 g/m² (Sinclair and Horie, 1989). In general, C₃ species tend to have greater SLN than C₄ species (Anten et al., 1995). The vertical profile of SLN within a canopy also affects the RUE (Hammer and Wright, 1994), as can environmental factors such as the nature of incident solar radiation, air temperature (T_a), atmospheric CO₂ partial pressure (C_a), and plant water status. The RUE increases with greater proportion of diffuse solar radiation (e.g., Sinclair et al., 1992), which is also predicted with a theoretical analysis that incorporates leaf-level photosynthesis light responses (Hammer and Wright, 1994). Their work predicted an increase of ca 40% in RUE of soybean crops (at SLN of 3 g/m²) with full diffuse solar radiation in case of heavy cloud cover.

Crop models commonly use simple indices as multipliers to capture effects of T_a and C_a and plant water status. For example, in APSIM-wheat it is assumed that RUE is not affected by temperature in the range of 10–25°C (http://www.apsim.info/Documentation/Model,CropandSoil/CropModuleDocumentation/Wheat.aspx), but is reduced at either higher or lower temperatures. In comparison, this range is 17–33°C in the CERES-Maize model (López-Cedrón et al., 2005). This insensitivity of RUE over broad ranges of temperatures corresponds with findings that leaf photosynthesis is insensitive to temperature within these ranges (Sage and Kubien, 2007). In modeling studies exploring impacts of climate change on crop productivity (Lobell et al., 2015), RUE is increased with elevated C_a in C₃ species but is not changed in C₄ species, in line with the known differences in response to photosynthesis. In water-limited situations, RUE is reduced in line with the relative transpiration achieved by the crop, which is determined from the balance between atmospheric demand and soil water uptake (Chapman et al., 1993). The RUE approach is a simpler way to model crop growth than the PLR models (used in the first type of canopy photosynthesis modeling), but it involves invoking a number of empiricisms to deal with responses to environmental factors and crop physiological attributes of the crop, which can reduce the predictive power of the RUE approach.

Avenues to Improve Connections in the Cross-Scale Modeling Framework with Environmental Factors and Crop Physiological Attributes

Success of cross-scale modeling depends on (1) the reliability of models at each level and (2) effective connections across levels of modeling. In previous sections, we have discussed the emerging framework for cross-scale modeling that connects photosynthesis models at the biochemical/leaf level with those at the canopy/crop level, with an emphasis on capture of light and its conversion into photosynthates and canopy biomass. Conveniently, this established framework can serve as the basis to connect other environmental factors and crop physiological attributes into the cross-scale model (Figure 1). Nitrogen is a critical factor in this connection and we will detail the use of SLN to exemplify the two considerations for cross-scale modeling: (1) generation and modeling of SLN as an emergent consequence of plant growth and development dynamics, and (2) developments for connecting SLN into the cross-scale modeling framework using the sun-shade leaf modeling approach.

Crop Physiological Attribute: Specific Leaf Nitrogen (SLN)

SLN is an emergent consequence of plant growth and development dynamics and has been modeled on this basis in crop models (Hammer et al., 2010). The rate of nitrogen (N) uptake of a crop is closely linked to leaf area expansion (Lemaire et al., 2007), particularly early in the crop cycle, prior to stem elongation (van Oosterom et al., 2010). Pre-anthesis allocation of N across organs follows a hierarchical pattern, where the demand for structural stem N and the N demand of expanding leaves is met first (Hammer et al., 2010). For leaves, this demand is represented by the critical SLN. Any additional N that is available once these demands have been met is subsequently allocated to these organs as luxury or storage N, which reflects the sink-limited crop growth modeling approach (Fatichi et al., 2014). Because larger stems require more structural N, stem size can reduce luxury leaf N uptake beyond the critical SLN. Similarly, a large canopy size (high LAI) will reduce SLN through dilution. As a consequence, the SLN of a crop is an emergent consequence of the complex interactions among total crop N uptake, relative organ size (which determines crop N demand) and the hierarchy of N allocation (van Oosterom et al., 2010).

SLN is a key driver of both crop-level RUE (e.g., Sinclair and Horie, 1989) and leaf-level photosynthesis (i.e., leaf CO₂ assimilation rate) (e.g., Evans, 1989; Grindlay, 1997). Below the critical SLN, the rate of light-saturated (or CO₂ limited) net photosynthesis increases linearly with SLN, although the response differs across species (Field and Mooney, 1983; Sinclair and Horie, 1989; Anten et al., 1995) and can also depend on environmental conditions. At SLN values above the critical level, however, photosynthesis rates reach a maximum (Field and Mooney, 1983; Sinclair and Horie, 1989), which is possibly linked to either light and/or the supply of CO₂ being the limiting factor (Evans, 1989). One approach to modeling leaf-level photosynthesis that incorporates SLN and is adopted in some PLR models is to associate some key photosynthetic parameters with SLN (e.g., A_max, Hammer and Wright, 1994). This approach is also applicable for driving the biochemical photosynthesis models with crop physiological attributes, which can be done by establishing relationships between biochemical photosynthesis model parameters (e.g., maximum rate of Rubisco carboxylation, V_cmax) and SLN (e.g., de Pury and Farquhar, 1997). This approach allows SLN, which is often related to canopy-level RUE, to be connected with the leaf-level models, and thus facilitates effective connections across levels of modeling.

Environmental Factors: Air Temperature and CO₂

Environmental factors such as air temperature (T_a) and atmospheric CO₂ partial pressure (C_a) should be accounted for in the cross-scale modeling framework (Figure 1). Like solar radiation, T_a also varies diurnally and seasonally, which can also be modeled, for example, using the approach of Parton and Logan (1981). T_a influences leaf photosynthesis because it is a key determinant of leaf temperature (T_l) (Monteith and Unsworth, 2013b).

One of the early studies of photosynthetic responses to T_l and C_a was on quantum efficiency of photosynthesis (Ehleringer and Björkman, 1977). Various studies quantified the effects of C_a on the empirical convexity factor of some PLR models (Ogren, 1993; Lewis et al., 1999) (attributed to the CO₂ effect on photorespiration; Yin and Struik, 2015), and on the maximum rate of photosynthesis and quantum efficiency (Cannell and Thornley, 1998). In general, increases in T_l or C_a also increase values of some PLR model parameters. However, the combined effects of T_l and C_a on model parameters becomes more complex to analyse (Cannell and Thornley, 1998). The more aggregated nature of PLR models means that model parameters often represent a combination of biochemical processes of photosynthesis, each of which may respond differently to environmental effects. Crop models using the more aggregated forms of photosynthesis modeling (PLR or RUE) often incorporate scaling factors as multipliers to account for effects of temperature and C_a on growth (Jones et al., 2003; Holzworth et al., 2014; Lobell et al., 2015). Hence, the effects of T_l and C_a in crop models using these empirical formalisms cannot be estimated as reliably as with biochemical photosynthetic models.

Connecting Biochemical Models of Photosynthesis into the Cross-Scale Modeling Framework

An approach to reduce the empiricism at the biochemical/leaf level in cross-scale modeling involves using models that can better capture the biochemical processes of photosynthesis and, at the same time, ensures effective connections across levels of modeling. This was pioneered by Yin and van Laar (2005), who connected the biochemical models of photosynthesis with the GECROS crop model through upscaling to canopy photosynthesis with the sun-shade leaf modeling approach. This cross-scale modeling approach was used by Yin and Struik (2008) to simulate likely consequences on rice yield of introducing the C₄ pathway into rice. In a later study, Gu et al. (2014) demonstrated that the cross-scale model could be used to explore effects of natural variation in photosynthetic attributes on biomass accumulation of rice. Yin and Struik (2015) have utilized the cross-scale modeling framework and evaluated constraints to the potential efficiency of converting solar energy into phytoenergy along the scales of biological organization from leaf biochemistry to canopy physiology and crop biomass. However, the latter two studies stopped short of exploring effects on grain yield because of uncertainties related to the prediction of grain number. The choice of models at both the biochemical/leaf and canopy/crop level are equally important for bridging the gap between photosynthetic manipulation at the biochemical level and crop productivity. Another canopy photosynthesis modeling study, which was also developed through upscaling of biochemical models, was undertaken to explore consequences of changing Rubisco kinetic properties on daily canopy photosynthesis (Zhu et al., 2004; Long et al., 2006). This study, however, was limited to daily predictions, because the simulation model lacked the two-way connection between the biochemical models and crop growth and development dynamics. In the following section, we will discuss strategies for connecting the biochemical models of photosynthesis into the cross-scale modeling framework to overcome issues of connectivity.

Biochemical Models of C₃ and C₄ Leaf Photosynthesis

The importance of Ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco) in determining photosynthesis has been recognized in early studies (see overview in von Caemmerer, 2013). Rubisco catalyses the competing reactions of the carboxylation [first step of the photosynthetic carbon reduction (PCR) cycle] and oxygenation [first step of the photorespiratory carbon oxidation (PCO) cycle] of ribulose-1,5-bisphosphate (RuBP) (Figure 1). This led to the development of biochemical photosynthesis models based on Rubisco kinetic properties and the two cycles (see review of von Caemmerer et al., 2009). The model of Farquhar et al. (1980) is one of these, and will be referred to here as the C₃ photosynthesis model. This model assumes that net photosynthesis is determined by the minimum (Equation 2) of either RuBP-saturated (Rubisco-limited) or RuBP-regeneration-limited (electron-transport-limited) CO₂ assimilation rate (Equations 3, 4 respectively). Rubisco-limited photosynthesis is comparable to the CO₂-limited photosynthesis described by Blackman's PLR model, whereas electron-transport-limited photosynthesis is comparable to the light-limited photosynthesis. Farquhar (1989) demonstrated that the C₃ photosynthesis model, intended at the biochemical level, is also applicable for photosynthesis at the leaf level given the assumptions that photosynthetic attributes are identical for all chloroplasts in the leaf and that light distribution inside the leaf is homogenous (Song et al., 2013). The utility of the C₃ photosynthesis model has been in helping to interpret gas exchange measurements of steady-state CO₂ assimilation (A) of leaves (e.g., response of A to intercellular CO₂ partial pressure, A/C_i curves) and predicting the effects on photosynthesis of variation in genotype, photosynthetic photon flux density (PPFD), leaf temperature, and intercellular CO₂ and O₂ partial pressures (von Caemmerer et al., 2009). The main equations of the C₃ photosynthesis model (von Caemmerer, 2000) are:

$\begin{array}{ll}A=\text{min}\left\{A_{\text{c}},A_{\text{i}}\right\}& (2)\end{array}$

$\begin{array}{ll}{A}_{\text{c}}=\frac{\left(C_{\text{c}}-{\Gamma }_{*}\right)V_{\text{cmax}}}{C_{\text{c}}+K_{\text{c}}(1+{\text{O}}_{\text{c}}/K_{\text{o}})}-R_{\text{d}}& (3)\end{array}$

$\begin{array}{ll}{A}_{\text{j}}=\frac{\left(C_{\text{c}}-{\Gamma }_{*}\right)J}{4C_{\text{c}}+8{\Gamma }_{*}}-R_{\text{d}}& (4)\end{array}$

where A is the net CO₂ assimilation rate, C_c and O_c are the chloroplastic CO₂ and O₂ partial pressures respectively, R_d is the respiration other than that from the PCO cycle, Γ_* is half the reciprocal of the relative CO₂/O₂ specificity of Rubisco multiplied by O_c and is also defined by the CO₂ compensation point in the absence of R_d (Figure 2.11, von Caemmerer, 2000), V_cmax is the maximum rate of Rubisco carboxylation, K_c and K_o are the Michaelis Menten constants of Rubisco carboxylation and oxygenation, and J is the electron transport rate.

The photosynthetic electron transport chain can be limited by either NADPH (the reduced form of nicotinamide adenine dinucleotide phosphate) or ATP (adenosine triphosphate) supply, depending on which of the three modes of electron transport (i.e., linear, cyclic, and pseudocyclic electron transport) are active (von Caemmerer, 2000). Equation (4), the most used expression, assumes 100% linear electron transport and that NADHP supply limits overall leaf photosynthesis (Yin et al., 2009). However, this may not always be the case in leaves. For example, if ATP supply is limiting with 100% linear electron transport, the factors 4 and 8 in the denominator of Equation (4) are replaced by 4.5 and 10.5, respectively (Yin et al., 2009). Due to the uncertainty on whether NADPH or ATP is limiting, different forms of Equation (4) are used. This uncertainty can be eliminated by using a generalized stoichiometry of the electron transport chain (extended-electron-transport-chain) model that incorporates the three modes of electron transport for C₃ photosynthesis (Yin et al., 2009). A C₄ equivalent of the model is presented in Yin and Struik (2009). The extended model quantifies the photosynthetic quantum yield (α) based on the photochemical efficiencies of photosystem I and II and the fraction of total photosystem I electron fluxes that follows the cyclic and pseudocyclic pathways (Yin and Struik, 2015). The extended model is valuable for the analysis of photosynthetic regulation via the electron transport pathways in response to environmental stresses (Yin et al., 2004, 2009). However, there are still uncertainties in a number of parameters in the model (e.g., number of H⁺ transported by cyclic electron transport; Yin and Struik, 2009). In addition, Equation (4) performed similarly to the extended-electron-transport-chain model when used to infer values of V_camx and J_max of the C₃ photosynthesis model from A/C_i curves (Yin et al., 2004). In fact, this is also the case for the ATP-supply-limited version of Equation (4). This implies that for the purpose of reproducing A/C_i curves for cross-scale modeling, use of the extended-electron-transport-chain model may not be necessary.

The main equations for the biochemical model of C₄ photosynthesis (von Caemmerer, 2000), based on previous work of Berry and Farquhar (1978) and Collatz et al. (1992), adopts the main equations of the C₃ photosynthesis model (i.e., Equations 2–4) with modifications to capture the coordinated function of mesophyll and bundle-sheath cells. In the C₄ photosynthesis model, A_c and A_j are given by:

$\begin{array}{ll}{A}_{\text{c}}=\frac{\left(C_{\text{s}}-{\gamma }_{*}{O}_{\text{s}}\right)V_{\text{cmax}}}{C_{\text{s}}+K_{\text{c}}(1+O_{\text{s}}/K_{\text{o}})}-R_{\text{d}}& (5)\end{array}$

$\begin{array}{ll}{A}_{\text{j}}=\frac{\left(C_{\text{s}}-{\gamma }_{*}{O}_{\text{s}}\right)\left(1-x\right)J_{\text{t}}}{3\left(C_{\text{s}}+7/3{\gamma }_{*}{O}_{\text{s}}\right)}-R_{\text{d}}& (6)\end{array}$

where γ_* is half the reciprocal of the relative CO₂/O₂ specificity of Rubisco, C_s and O_s are the bundle-sheath CO₂ and O₂ partial pressure [which are calculated with additional equations, described in von Caemmerer (2000), reflecting the coordinated function of mesophyll and bundle-sheath cells], respectively. J_t is the total electron transport rate from both the mesophyll and bundle-sheath cells and the factor (1 − x) represents the proportion of the total electrons that are available to the bundle-sheath cells, while the rest are required by the mesophyll cells.

Connecting Biochemical Photosynthesis Models to Environmental Factors and Crop Physiological Attributes

Biochemical photosynthesis models can be connected to crop models by utilizing the emerging cross-scale modeling framework (Figure 1). The first step in this approach, which involves upscaling to canopy photosynthesis, has been achieved through the use of the simpler representations of canopy structure (i.e., LAI and k) such as the multi-layer (Leuning et al., 1995), the sun-shade (de Pury and Farquhar, 1997), the big-leaf (which aggregates absorbed radiation and photosynthetic capacity into a single element) (Sellers et al., 1992) modeling approaches and 3D models such as the RATP model (Sinoquet et al., 2001). However, upscaling to cross-scale modeling through the use of the sun-shade modeling approach is an avenue to achieve a balance between simplicity and robustness (Yin and van Laar, 2005). In the following section, we will discuss strategies for connecting environmental factors (i.e., T_a, C_a, and water) and crop physiological attributes (e.g., SLN) into the cross-scale modeling framework.

An issue for canopy photosynthesis modeling is if and how to include spatial variability within the canopy for environmental factors like T_a and C_a. Many authors resort to the assumption that these environmental factors do not vary spatially within the canopy (Leuning et al., 1995; Wang and Leuning, 1998; Yin and van Laar, 2005), while others use empirical functions, such as an exponentially decreasing wind speed through canopy for estimating leaf boundary layer conductance, which affects diffusion of C_a into leaves (Yin and van Laar, 2005). Spatial variability of environmental parameters within the canopy, such as T_a, can also be captured with 3D plant architecture modeling (e.g., Sinoquet et al., 2001). However, the assumptions for omitting spatial variability are supported by observations (Wang and Leuning, 1998) that the effects on canopy photosynthesis of including spatial variation for T_a, vapor pressure deficit (VPD) and C_a in simulations are only minor (within 5%) under a wide range of soil water availabilities and meteorological conditions. This is further supported by the finding that canopy photosynthesis can be closely approximated by photosynthesis of the sunlit fraction (Hirose, 2005). It could be that a large part of canopy photosynthesis is contributed by leaves in the upper part of the canopy, which experience environmental conditions close to those above the canopy, making it reasonable to omit the spatial variability in T_a, VPD, and C_a within canopies from simulation models.

As seen in the Section Utilizing Relationships between Crop Growth and Light Interception, T_a can have a significant impact on RUE and crop growth, because it affects leaf temperature (T_l), which in turn affects leaf-level photosynthesis. The question of how to estimate T_l is covered in subsequent paragraphs. First, parameterizing effects of T_l on photosynthesis is possible by using studies that quantify the response of biochemical model parameters to T_l (Bernacchi et al., 2001, 2002, 2003; Massad et al., 2007; Braune et al., 2009; Boyd et al., 2015; Yin et al., 2016). Temperature responses of the main C₃ model parameters (V_cmax, J_max, K_c, K_o, and Γ_*) have been studied both in vivo and in vitro in recent years. In vivo data sets are most comprehensive for model C₃ species such as Arabidopsis thaliana and Nicotiana tabacum (Bernacchi et al., 2001, 2002, 2003; Walker et al., 2013), although data sets for C₃ and C₄ crop species are also becoming available (Massad et al., 2007; Braune et al., 2009; Yin et al., 2016). In vitro data for C₃ species like wheat (Cousins et al., 2010) and the model C₄ species Setaria viridis have also appeared (Boyd et al., 2015). To connect T_l into canopy photosynthesis modeling, it has been suggested that spatial variation of T_l within the canopy is required. 3D canopy architectural models could be used to describe this spatial variation (Sinoquet et al., 2001). However, Wang and Leuning (1998) demonstrated by using the sun-shaded leaf modeling approach, assuming that T_l was the same within each fraction but differed between them, that a reasonable approximation resulted. This has been implemented in many studies (de Pury and Farquhar, 1997; Wang and Leuning, 1998; Dai et al., 2004; Yin and van Laar, 2005).

The difficulty in simulating T_l is that it is interlinked with transpiration. Diffusion of C_a into leaves through stomata (C_i) driving photosynthesis is affected by stomatal conductance, which is driven by the balance between atmospheric demand and crop soil water uptake. These complex interactions are unavoidable. An emerging framework for capturing these interactions in well-watered situations is by coupling the leaf-level biochemical photosynthesis models with the isothermal form of the Penman-Monteith equation (for T_l simulation) and a stomatal conductance model (for C_i simulation). The Penman-Monteith equation (Monteith, 1965a; Monteith and Unsworth, 2013b) reflects the interdependency between leaf energy balance and transpiration, which depends on diffusion of water vapor out of leaves through stomata and the leaf boundary layer and on the VPD of the surrounding air. Many authors have taken this path and captured these interactions for leaf-photosynthesis modeling and connected it with canopy photosynthesis modeling through the use of the sun-shade modeling approach (Wang and Leuning, 1998; Kim and Lieth, 2003; Yin and van Laar, 2005; Yin and Struik, 2009). Furthermore, some of these canopy photosynthesis models have been implemented in crop models (Yin and van Laar, 2005; Yang et al., 2009), achieving frameworks in line with the cross-scale modeling approach. Given this framework for capturing connections across scales, there remain choices of models for capturing the interlinked nature of T_l, transpiration, and photosynthesis.

Canopy photosynthesis models that respond to C_a, which affects C_i, involve incorporating a stomatal conductance model. The most widely used leaf stomatal conductance models are those that relate stomatal conductance to photosynthesis (e.g., the BWB-type models developed and named after the authors in Ball et al., 1987) and multiplicative models (e.g., Jarvis, 1976) based on environmental factors (for review of stomatal conductance models see Damour et al., 2010). Stomatal conductance for CO₂ can be converted to that for water vapor, or vice versa, by assuming water vapor diffuses through stomata at a rate that is 1.6 times faster than CO₂ (Dai et al., 2004; Yin and van Laar, 2005). This is modeled by using Graham's law of effusion, calculated as the square root of the ratio of the molecular weight of CO₂ over H₂O. The BWB-type models have subsequently been improved by several authors (Leuning, 1995; Yin and Struik, 2009), while retaining the concept that stomatal conductance is driven by photosynthesis. Coupling of stomatal conductance models to biochemical models of photosynthesis (Collatz et al., 1992; Leuning, 1995; Kim and Lieth, 2003; Yin and Struik, 2009; Li et al., 2012) can facilitate photosynthesis estimation in response to C_a. Wang and Leuning (1998) incorporated a BWB-type stomatal conductance model into canopy photosynthesis modeling through the use of the sun-shade modeling approach. They assumed that stomatal conductance (per leaf area basis) was the same within each fraction but differed between them, and concluded that this generated a reasonable approximation. This is a simple and robust approach for connecting C_a into canopy photosynthesis modeling and has been adopted in other work (Dai et al., 2004; Yin and van Laar, 2005).

The emerging framework for capturing the interactions between T_l, transpiration and photosynthesis is subsequently revised to capture effects of water-limited situations. Many authors incorporated empirical effects on some of the biochemical model parameters (see references cited in Li et al., 2012), assuming that water stress directly affects photosynthesis. In contrast, Li et al. (2012) modeled effects of water stress by incorporating effects of soil water as an empirical impact function in the BWB-type model without modifying photosynthesis. This can be upscaled to the canopy level as described above. However, the similarity in both approaches to incorporating water effects is that stomatal conductance is responsive to photosynthesis, which may not be the case in water-limited situations. Approaches to water limitation used in crop models may provide an avenue to reduce the empirical approach currently used in biochemical photosynthesis models. When water becomes limiting, some crop models drive crop growth via transpiration, which is estimated by the balance between atmospheric demand and crop soil water uptake (Monteith and Greenwood, 1986; Monteith, 1988; Hammer et al., 2010). The switch between light-limited and water-limited crop growth depends on the estimated plant water status (Chapman et al., 1993; Hammer et al., 2010). A more mechanistic method involving the coordination of the controls of stomatal aperture, transpiration and abscisic acid (Tardieu et al., 2015) can be used to estimate transpiration, but the simpler approach for estimating transpiration in crop models has proven to be robust when applied across a diverse range of environments (Hammer et al., 2010). This implies that in water-limited situations, photosynthesis is responsive to stomatal conductance.

A major crop physiological attribute affecting canopy and leaf photosynthesis is SLN (Section Avenues to Improve Connections in the Cross-Scale Modeling Framework with Environmental Factors and Crop Physiological Attributes). Nitrogen is needed to support photosynthetic machineries via Rubisco for the photosynthetic carbon reduction cycle and thylakoid membrane proteins for the electron transport chain. Partitioning of leaf nitrogen to these photosynthetic components is a complex topic and is probably species dependent (Evans, 1989; Buckley et al., 2013). Fortunately, without modeling these complexities, canopy photosynthesis can be linked to canopy nitrogen content through upscaled PLR models that respond to SLN (Hammer and Wright, 1994). This approach is also applicable for obtaining canopy photosynthesis based on the biochemical photosynthesis models (de Pury and Farquhar, 1997). Linking biochemical photosynthesis model parameters to SLN becomes a key for connecting across scales, because model parameters are quantitatively related to SLN (Evans, 1983, 1989; Braune et al., 2009; Archontoulis et al., 2012). Because of this association, total nitrogen content of sunlit and shaded fractions can be used to drive the biochemical photosynthesis models when scaling up to the canopy level (de Pury and Farquhar, 1997).

Extending Cross-Scale Modeling for Assessing Genetic Manipulations of Photosynthesis

Current canopy photosynthesis modeling based on the biochemical photosynthesis models can be readily used for assessing the consequences of genetic manipulations of photosynthesis on crop growth and production. Yin and Struik (2008) incorporated a canopy photosynthesis model, based on the C₄ photosynthesis model, into the GECROS crop model to assess the consequences of C₄ photosynthesis on rice crop production. They predicted a yield increase of 23% with the full introduction of the C₄ pathway into rice. Improvement in Rubisco kinetic properties have also been assessed for consequences on canopy photosynthesis (Zhu et al., 2004; Long et al., 2006). Given the wide range of possibilities for photosynthetic manipulation there is a need to extend the biochemical models and possibly the cross-scale modeling framework. Three important areas in pursing this are (1) extending the biochemical photosynthesis models to capture genetic manipulations in photosynthesis, (2) connecting model extensions across scales, and (3) capturing pleiotropic effects of genetic manipulations in photosynthesis. These issues are discussed in terms of framing the cross-scale modeling for genetic manipulations using examples based on current knowledge for three specific potential manipulations.

Improving Rubisco Kinetic Properties

The upscaled biochemical photosynthesis models (Section Connecting Biochemical Photosynthesis Models to Environmental Factors and Crop Physiological Attributes) can be readily used to estimate consequences of manipulations in Rubisco kinetics on canopy photosynthesis. However, an effect of changing Rubisco kinetics, K_c in particular, is that it can also affect the maximum catalytic turnover of carboxylase per Rubisco site, k_cat (Whitney et al., 2011; Evans, 2013; Sharwood and Whitney, 2014). In addition, V_cmax is the product of k_cat and the number of moles of Rubisco sites per unit of leaf area, n_R (Zhu et al., 2004; Evans, 2013). These pleiotropic effects will affect the calculation of CO₂ assimilation rate and should be captured in the cross-scale modeling. However, n_R and the relationship between K_c and k_cat need to be defined. n_R can be calculated from measurements of Rubisco concentration in leaves, which provides the connection with SLN, which in turn is determined by the balance between crop nitrogen uptake and rate of leaf area growth [Section Crop Physiological Attribute: Specific Leaf Nitrogen (SLN)]. However, the relationship between K_c and k_cat may be difficult to predict as different approaches for manipulating Rubisco enzymes can lead to different relationships (Evans, 2013). On the other hand, when comparing K_c and k_cat of Rubisco enzymes, there is a strong linear relationship (Evans, 2013) that can be parameterized by a slope and intercept. Capturing these pleiotropic effects in the cross-scale modeling should allow more realistic simulations of canopy photosynthesis.

Mesophyll Conductance

The biochemical photosynthesis models have already been extended to include diffusion of C_a from the surrounding air to the leaf intercellular airspace (C_i) by incorporating the leaf boundary layer conductance and stomatal conductance and have been incorporated into canopy photosynthesis models (Wang and Leuning, 1998). However, mesophyll conductance, which affects diffusion of C_i to the carboxylating site of Rubisco (C_c), is also required in modeling due to its significance in controlling leaf photosynthesis (Flexas et al., 2008; Terashima et al., 2011) and for considering mesophyll conductance manipulations (Flexas et al., 2012). The framework to include mesophyll conductance in modeling CO₂ diffusion, using Ficks's first law of diffusion for CO₂, is given by:

$\begin{array}{ll}{C}_{\text{c}}=C_{\text{a}}-\frac{A}{g_{\text{bl}}}-\frac{A}{g_{\text{s}}}-\frac{A}{g_{\text{m}}}& (7)\end{array}$

where C_c and C_a are the CO₂ partial pressure at the carboxylating site of Rubisco inside chloroplasts and of the surrounding air, respectively, g_bl, g_s and g_m are the leaf boundary layer, stomatal and mesophyll conductance for CO₂ respectively, and A is the net CO₂ assimilation rate.

Use of Equation (7) relies on revising C_i-based biochemical model parameters to incorporate effects of g_m (i.e., C_c-based values) and parameterizing of g_m. The first issue is accommodated by the increasing availability of C_c-based values (Bernacchi et al., 2002; Cousins et al., 2010). For the second issue, environmental factors (e.g., air temperature, soil water, and C_a), crop physiological attributes (e.g., leaf N), and leaf anatomical parameters (e.g., mesophyll cell wall thickness) can be used to determine g_m through the use of empirical relationships (Evans et al., 2009; Flexas et al., 2012; Tomás et al., 2013). These empirical approaches rely on experimental measurements for establishing the correlation, which can be facilitated by developments in measurement techniques such as gas exchange, in combination with carbon isotope discrimination (Pons et al., 2009). Such techniques allow the response of g_m to soil N, soil water, and leaf temperature to be parameterized (Evans and von Caemmerer, 2013; Barbour and Kaiser, 2016). Established correlations with empirical approaches, however, may not extrapolate reliably to yet unexplored parts of the simulation landscape. For example, g_m responses to environmental factors and crop physiological attributes may not be estimated using known empirical relationships when g_m is manipulated by altering expression of aquaporins on cell membranes (Flexas et al., 2012) or anatomical features of leaves such as the thickness of mesophyll cell walls (Terashima et al., 2011). An additional layer of complexity is introduced if pleiotropic effects of g_m manipulation are considered. Work on characterizing effects of g_m manipulation on a range of photosynthesis related attributes (e.g., total Rubisco activity, respiration rate, and g_s) can provide information on possible pleiotropic effects (Flexas et al., 2006; Barbour et al., 2016), which should help parameterize the cross-scale modeling. Recently, a more mechanistic approach for modeling g_m was presented (Evans and von Caemmerer, 2013). However, it should be noted that use of more complex models will need parameterization of responses to environmental and crop physiological attributes for the cross-scale modeling. Effective modeling involves careful consideration of the extent of complexity actually required (Hammer et al., 2006).

Introducing Chlorophyll d and f into the Light Harvesting Antenna of Photosystems

Light absorption by Chlorophyll a and b, which are the most common chlorophylls in the light harvesting antenna of crop species, can only utilize wavebands in the spectrum up to 700 nm (Chen and Blankenship, 2011). Introducing chlorophyll d and f could offer the possibility of pushing the boundary toward 750 nm, which increases available PAR by 19% (Chen and Blankenship, 2011). Effects of this can be estimated by existing canopy light distribution models (e.g., sun-shade models) if k-values can be revised. However, the biochemical photosynthesis models commonly use an empirical, non-rectangular hyperbola function to describe electron transport rate (J) in terms of PPFD (e.g., Equation 2.13, von Caemmerer, 2000). Unfortunately, the connection between empirical parameters of the non-rectangular hyperbola function and compositions of chlorophyll types is not clear. In addition, these new chlorophyll types will alter the spectral quality of light in the canopy by changing the ratio between red (660 nm) and far-red (730 nm) light. This could interfere with the phytochromes in plants that regulate shade avoidance and other phytochrome-related physiological functions (Evans, 2013). It has been shown that lower red:far-red ratio can cause a lower chlorophyll a:b ratio (Pons and de Jong-van Berkel, 2004) as well as influence bud outgrowth and tillering (Ballaré and Casal, 2000; Lafarge et al., 2002). These possible pleiotropic effects of introducing new chlorophyll types remain difficult to incorporate at this stage.

Concluding Remarks

The emerging cross-scale modeling framework connecting biochemical/leaf and canopy/crop levels (Figure 1) has the capacity to link genetic manipulation of photosynthesis to crop yield. The success of cross-scale modeling is built on (1) the reliability of models at each scale and (2) how well the connections are captured across scales. Connecting the biochemical photosynthesis models into the cross-scale modeling framework allows clearer links to the biochemical processes of photosynthesis, based on which consequences of photosynthetic manipulations can be reliably estimated. This can be further improved by the advancing understanding of photosynthetic responses to environmental and physiological attributes and further modeling efforts. The crop scale models with the concept of both source- and sink-limited growth provide important effects that can regulate the biochemical photosynthetic models via crop scale nitrogen and water status, which determine SLN and influence canopy conductance in water-limited situations. Development of the cross-scale modeling framework using the gene-to-phenotype modeling approach can potentially accelerate progress in improving crop resource capture efficiency to support crop improvement through genetic manipulation of photosynthesis.

Author Contributions

GH took part in securing the funding. AW, YS, EvO, and GH contributed substantially to the conception of this work, AW and YS drafted the work with help of EvO and GH. AW, EvO, and GH critically revised the work.

Funding

The work is financially supported by the Australian Research Council through the Centre of Excellence for Translational Photosynthesis.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge helpful discussions with Professor Graham Farquhar in relation to aspects of this paper.

References

Akhkha, A. (2010). Modelling photosynthetic light-response curve in Calotropis procera under salinity or water deficit stress using non-linear models. J. Taibah Univ. Sci. 3, 49–57. doi: 10.1016/S1658-3655(12)60020-X

CrossRef Full Text | Google Scholar

Anten, N. P. R., Schieving, F., and Werger, M. J. A. (1995). Patterns of light and nitrogen distribution in relation to whole canopy carbon gain in C3 and C4 mono- and dicotyledonous species. Oecologia 101, 504–513. doi: 10.1007/BF00329431

CrossRef Full Text | Google Scholar

Archontoulis, S. V., Yin, X., Vos, J., Danalatos, N. G., and Struik, P. C. (2012). Leaf photosynthesis and respiration of three bioenergy crops in relation to temperature and leaf nitrogen: how conserved are biochemical model parameters among crop species? J. Exp. Bot. 63, 895–911. doi: 10.1093/jxb/err321

PubMed Abstract | CrossRef Full Text

Ball, J. T., Woodrow, I., and Berry, J. (1987). “A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions,” in Progress in Photosynthesis Research, ed J. Biggins (Dordrecht: Martinus Nijhoff Publishers), 221–224.

Google Scholar

Ballaré, C. L., and Casal, J. J. (2000). Light signals perceived by crop and weed plants. Field Crops Res. 67, 149–160. doi: 10.1016/S0378-4290(00)00090-3

CrossRef Full Text | Google Scholar

Barbour, M. M., Bachmann, S., Bansal, U., Bariana, H., and Sharp, P. (2016). Genetic control of mesophyll conductance in common wheat. New Phytol. 209, 461–465. doi: 10.1111/nph.13628

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbour, M. M., and Kaiser, B. N. (2016). The response of mesophyll conductance to nitrogen and water availability differs between wheat genotypes. Plant Sci. 251, 119–127. doi: 10.1016/j.plantsci.2016.03.012

PubMed Abstract | CrossRef Full Text

Bernacchi, C. J., Pimentel, C., and Long, S. P. (2003). In vivo temperature response functions of parameters required to model RuBP-limited photosynthesis. Plant Cell Environ. 26, 1419–1430. doi: 10.1046/j.0016-8025.2003.01050.x

CrossRef Full Text | Google Scholar

Bernacchi, C. J., Portis, A. R., Nakano, H., von Caemmerer, S., and Long, S. P. (2002). Temperature response of mesophyll conductance. Implications for the determination of Rubisco enzyme kinetics and for limitations to photosynthesis in vivo. Plant Physiol. 130, 1992–1998. doi: 10.1104/pp.008250

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, A. R. Jr., and Long, S. P. (2001). Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant Cell Environ. 24, 253–259. doi: 10.1111/j.1365-3040.2001.00668.x

CrossRef Full Text | Google Scholar

Berry, J., and Farquhar, G. (1978). “The CO₂ concentrating function of C4 photosynthesis. A biochemical model. Photosynthesis 77,” in Proceedings of the Fourth International Congress on Photosynthesis, eds D. O. Hall, J. Coombs, and T. J. Goodwin (London: Biochemical Society), 119–131.

Blackman, F. F. (1905). Optima and limiting factors. Ann. Bot. 19, 281–296.

Google Scholar

Boyd, R. A., Gandin, A., and Cousins, A. B. (2015). Temperature response of C4 photosynthesis: biochemical analysis of Rubisco, Phosphoenolpyruvate Carboxylase and Carbonic Anhydrase in Setaria viridis. Plant Physiol. 169, 1850–1861. doi: 10.1104/pp.15.00586

PubMed Abstract | CrossRef Full Text | Google Scholar

Boysen Jensen, P. (1932). Die Stoffproduktion der Pflanzen. Jena: Gustav Fischer.

Braune, H., Mueller, J., and Diepenbrock, W. (2009). Integrating effects of leaf nitrogen, age, rank, and growth temperature into the photosynthesis-stomatal conductance model LEAFC3-N parameterised for barley (Hordeum vulgare L.). Ecol. Model. 220, 1599–1612. doi: 10.1016/j.ecolmodel.2009.03.027

CrossRef Full Text | Google Scholar

Brock, T. D. (1981). Calculating solar-radiation for ecological-studies. Ecol. Model. 14, 1–19. doi: 10.1016/0304-3800(81)90011-9

CrossRef Full Text | Google Scholar

Buckley, T. N., Cescatti, A., and Farquhar, G. D. (2013). What does optimization theory actually predict about crown profiles of photosynthetic capacity when models incorporate greater realism? Plant Cell Environ. 36, 1547–1563. doi: 10.1111/pce.12091

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, G. S. (1977). An Introduction to Environmental Biophysics. New York, NY: Springer-Verlag.

Google Scholar

Cannell, M. G. R., and Thornley, J. H. M. (1998). Temperature and CO₂ responses of leaf and canopy photosynthesis: a clarification using the non-rectangular hyperbola model of photosynthesis. Ann. Bot. 82, 883–892. doi: 10.1006/anbo.1998.0777

CrossRef Full Text | Google Scholar

Chapman, S. C., Hammer, G. L., and Meinke, H. (1993). A sunflower simulation-model.1. Model development. Agron. J. 85, 725–735. doi: 10.2134/agronj1993.00021962008500030038x

CrossRef Full Text | Google Scholar

Chen, M., and Blankenship, R. E. (2011). Expanding the solar spectrum used by photosynthesis. Trends Plant Sci. 16, 427–431. doi: 10.1016/j.tplants.2011.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, T.-W., Nguyen, T. M. N., Kahlen, K., and Stützel, H. (2014). Quantification of the effects of architectural traits on dry mass production and light interception of tomato canopy under different temperature regimes using a dynamic functional–structural plant model. J. Exp. Bot. 65, 6399–6410. doi: 10.1093/jxb/eru356

PubMed Abstract | CrossRef Full Text | Google Scholar

Collatz, G. J., Ribas-Carbo, M., and Berry, J. A. (1992). Coupled photosynthesis-stomatal conductance model for leaves of c4 plants. Aust. J. Plant Physiol. 19, 519–538. doi: 10.1071/PP9920519

CrossRef Full Text | Google Scholar

Cousins, A. B., Ghannoum, O., Von Caemmerer, S., and Badger, M. R. (2010). Simultaneous determination of Rubisco carboxylase and oxygenase kinetic parameters in Triticum aestivum and Zea mays using membrane inlet mass spectrometry. Plant Cell Environ. 33, 444–452. doi: 10.1111/j.1365-3040.2009.02095.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, Y., Dickinson, R. E., and Wang, Y.-P. (2004). A Two-Big-leaf model for canopy temperature, photosynthesis, and stomatal conductance. J. Clim. 17, 2281–2299. doi: 10.1175/1520-0442(2004)017<2281:ATMFCT>2.0.CO;2

CrossRef Full Text | Google Scholar

Damour, G., Simonneau, T., Cochard, H., and Urban, L. (2010). An overview of models of stomatal conductance at the leaf level. Plant Cell Environ. 33, 1419–1438. doi: 10.1111/j.1365-3040.2010.02181.x

PubMed Abstract | CrossRef Full Text | Google Scholar

de Pury, D. G. G., and Farquhar, G. D. (1997). Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 20, 537–557. doi: 10.1111/j.1365-3040.1997.00094.x

CrossRef Full Text | Google Scholar

de Wit, C. T. (1959). Potential photosynthesis of crop surfaces. Neth. J. Agric. Sci. 7, 141–149.

Google Scholar

de Wit, C. T. (1965). Photosynthesis of leaf canopies. Agric. Res. Rep. 663, 57.

Google Scholar

de Wit, C. T., Goudriaan, J., van Laar, H. H., Penning de Vries, F. W. T., Rabbinge, R., van Keulen, H., et al. (1978). Simulation of Assimilation, Respiration and Transpiration of Crops. Simulation Monographs. Wageningen: Pudco.

Google Scholar

Duncan, W. G., Loomis, R. S., Williams, W. A., and Hanau, R. (1967). A model for simulating photosynthesis in plant communities. Hilgardia 38:181. doi: 10.3733/hilg.v38n04p181

CrossRef Full Text | Google Scholar

Duvick, D. N. (2005). “The contribution of breeding to yield advances in maize (Zea mays L.),” in Advances in Agronomy, ed D. L. Sparks (San Diego, CA: Elsevier Academic Press Inc.), 83–145.

Duvick, D. N., and Cassman, K. G. (1999). Post–green revolution trends in yield potential of temperate maize in the north-central united states. Crop Sci. 39, 1622–1630. doi: 10.2135/cropsci1999.3961622x

CrossRef Full Text | Google Scholar

Ehleringer, J., and Björkman, O. (1977). Quantum yields for CO₂ uptake in C3 and C4 plants: dependence on temperature, CO₂, and O₂ concentration. Plant Physiol. 59, 86–90. doi: 10.1104/pp.59.1.86

PubMed Abstract | CrossRef Full Text | Google Scholar

El-Sharkawy, M. A. (2011). Overview: early history of crop growth and photosynthesis modeling. Biosystems 103, 205–211. doi: 10.1016/j.biosystems.2010.08.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, J. R. (1983). Nitrogen and photosynthesis in the flag leaf of wheat (Triticum aestivum L.). Plant Physiol. 72, 297–302. doi: 10.1104/pp.72.2.297

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, J. R. (1989). Photosynthesis and nitrogen relationships in leaves of C₃ plants. Oecologia 78, 9–19. doi: 10.1007/BF00377192

CrossRef Full Text | Google Scholar

Evans, J. R. (2013). Improving photosynthesis. Plant Physiol. 62, 1780–1793. doi: 10.1104/pp.113.219006

CrossRef Full Text | Google Scholar

Evans, J. R., and von Caemmerer, S. (2013). Temperature response of carbon isotope discrimination and mesophyll conductance in tobacco. Plant Cell Environ. 36, 745–756. doi: 10.1111/j.1365-3040.2012.02591.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, J. R., Kaldenhoff, R., Genty, B., and Terashima, I. (2009). Resistances along the CO₂ diffusion pathway inside leaves. J. Exp. Bot. 60, 2235–2248. doi: 10.1093/jxb/erp117

PubMed Abstract | CrossRef Full Text | Google Scholar

Evers, J. B., Huth, N. I., and Renton, M. (2009). “Light extinction in spring wheat canopies in relation to crop configuration and solar angle,” in 2009 Third International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications (PMA) (Beijing), 107–110.

Google Scholar

Farquhar, G. D. (1989). Models of integrated photosynthesis of cells and leaves. Philos. Trans. R. Soc. Lond. B 323, 357–367. doi: 10.1098/rstb.1989.0016

CrossRef Full Text | Google Scholar

Farquhar, G. D., and von Caemmerer, S. (1982). “Modelling of photosynthetic response to environmental conditions,” in Physiological Plant Ecology II, Vol. 12, eds O. L. Lange, P. S. Nobel, C. B. Osmond, H. Ziegler (Heidelberg: Springer), 549–587.

Farquhar, G. D., von Caemmerer, S., and Berry, J. A. (1980). A biochemical model of photosynthetic CO₂ assimilation in leaves of C3 species. Planta 149, 78–90. doi: 10.1007/BF00386231

PubMed Abstract | CrossRef Full Text | Google Scholar

Fatichi, S., Leuzinger, S., and Körner, C. (2014). Moving beyond photosynthesis: from carbon source to sink-driven vegetation modeling. New Phytol. 201, 1086–1095. doi: 10.1111/nph.12614

PubMed Abstract | CrossRef Full Text | Google Scholar

Field, C., and Mooney, H. A. (1983). Leaf Age and seasonal effects on light, water, and nitrogen use efficiency in a California Shrub. Oecologia 56, 348–355. doi: 10.1007/BF00379711

CrossRef Full Text | Google Scholar

Fischer, R. A. (2007). Understanding the physiological basis of yield potential in wheat. J. Agric. Sci. 145, 99–113. doi: 10.1017/S0021859607006843

CrossRef Full Text

Fischer, R. A., Rees, D., Sayre, K. D., Lu, Z. M., Condon, A. G., and Saavedra, A. L. (1998). Wheat yield progress associated with higher stomatal conductance and photosynthetic rate, and cooler canopies. Crop Sci. 38, 1467–1475. doi: 10.2135/cropsci1998.0011183X003800060011x

CrossRef Full Text | Google Scholar

Fischer, T., Byerlee, D., and Edmeades, G. (2014). Crop Yields and Global Food Security: Will Yield Increase Continue to Feed the World? ACIAR Monograph No. 158. Canberra, ACT: Australian Centre for International Agricultural Research.

Flexas, J., Barbour, M. M., Brendel, O., Cabrera, H. M., Carriquí, M., Díaz-Espejo, A., et al. (2012). Mesophyll diffusion conductance to CO₂: an unappreciated central player in photosynthesis. Plant Sci. 193, 70–84. doi: 10.1016/j.plantsci.2012.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Flexas, J., Ribas-Carbó, M., Diaz-Espejo, A., Galmés, J., and Medrano, H. (2008). Mesophyll conductance to CO₂: current knowledge and future prospects. Plant Cell Environ. 31, 602–621. doi: 10.1111/j.1365-3040.2007.01757.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Flexas, J., Ribas-Carbó, M., Hanson, D. T., Bota, J., Otto, B., Cifre, J., et al. (2006). Tobacco aquaporin NtAQP1 is involved in mesophyll conductance to CO₂ in vivo. Plant J. 48, 427–439. doi: 10.1111/j.1365-313X.2006.02879.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gent, M. P. N., and Seginer, I. D. O. (2012). A carbohydrate supply and demand model of vegetative growth: response to temperature and light. Plant Cell Environ. 35, 1274–1286. doi: 10.1111/j.1365-3040.2012.02488.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Goudriaan, J. (1977). Crop Micrometeorology: A Simulation Study. Wageningen: Pudoc.

Google Scholar

Goudriaan, J. (1988). The bare bones of leaf-angle distribution in radiation models for canopy photosynthesis and energy exchange. Agric. For. Meteorol. 43, 155–169. doi: 10.1016/0168-1923(88)90089-5

CrossRef Full Text | Google Scholar

Goudriaan, J., and van laar, H. H. (1978). Calculation of daily totals of the gross CO₂ assimilation of leaf canopies. Neth. J. Agric. Sci. 26, 373–382.

Google Scholar

Grindlay, D. J. C. (1997). Towards an explanation of crop nitrogen demand based on the optimization of leaf nitrogen per unit leaf area. J. Agric. Sci. 128, 377–396. doi: 10.1017/S0021859697004310

CrossRef Full Text | Google Scholar

Gu, J., Yin, X., Stomph, T.-J., and Struik, P. C. (2014). Can exploiting natural genetic variation in leaf photosynthesis contribute to increasing rice productivity? A simulation analysis. Plant Cell Environ. 37, 22–34. doi: 10.1111/pce.12173

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammer, G., Cooper, M., Tardieu, F., Welch, S., Walsh, B., van Eeuwijk, F., et al. (2006). Models for navigating biological complexity in breeding improved crop plants. Trends Plant Sci. 11, 587–593. doi: 10.1016/j.tplants.2006.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammer, G. L., Dong, Z., McLean, G., Doherty, A., Messina, C., Schussler, J., et al. (2009). Can changes in canopy and/or root system architecture explain historical maize yield trends in the U.S. corn belt? Crop Sci. 49, 299–312. doi: 10.2135/cropsci2008.03.0152

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammer, G. L., van Oosterom, E., McLean, G., Chapman, S. C., Broad, I., Harland, P., et al. (2010). Adapting APSIM to model the physiology and genetics of complex adaptive traits in field crops. J. Exp. Bot. 61, 2185–2202. doi: 10.1093/jxb/erq095

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammer, G. L., and Wright, G. C. (1994). A theoretical-analysis of nitrogen and radiation effects on radiation use efficiency in peanut. Aust. J. Agric. Res. 45, 575–589. doi: 10.1071/AR9940575

CrossRef Full Text | Google Scholar

Henderson, S., von Caemmerer, S., Farquhar, G. D., Wade, L. J., and Hammer, G. (1998). Correlation between carbon isotope discrimination and transpiration efficiency in lines of the C-4 species Sorghum bicolor in the glasshouse and the field. Aust. J. Plant Physiol. 25, 111–123. doi: 10.1071/PP95033

CrossRef Full Text | Google Scholar

Hirose, T. (2005). Development of the Monsi–Saeki Theory on Canopy structure and function. Ann. Bot. 95, 483–494. doi: 10.1093/aob/mci047

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzworth, D. P., Huth, N. I., deVoil, P. G., Zurcher, E. J., Herrmann, N. I., McLean, G., et al. (2014). APSIM - Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 62, 327–350. doi: 10.1016/j.envsoft.2014.07.009

CrossRef Full Text | Google Scholar

Jarvis, P. G. (1976). Interpretation of variations in leaf water potential and stomatal conductance found in canopies in field. Philos. Trans. R. Soc. Lond. B 273, 593–610. doi: 10.1098/rstb.1976.0035

CrossRef Full Text | Google Scholar

Jones, J. W., Hoogenboom, G., Porter, C. H., Boote, K. J., Batchelor, W. D., Hunt, L. A., et al. (2003). The DSSAT cropping system model. Eur. J. Agron. 18, 235–265. doi: 10.1016/S1161-0301(02)00107-7

CrossRef Full Text | Google Scholar

Kahlen, K., Wiechers, D., and Stützel, H. (2008). Modelling leaf phototropism in a cucumber canopy. Funct. Plant Biol. 35, 876–884. doi: 10.1071/FP08034

CrossRef Full Text | Google Scholar

Kim, S. H., and Lieth, J. H. (2003). A coupled model of photosynthesis, stomatal conductance and transpiration for a rose leaf (Rosa hybrida L.). Ann. Bot. 91, 771–781. doi: 10.1093/aob/mcg080

PubMed Abstract | CrossRef Full Text | Google Scholar

Lafarge, T. A., Broad, I. J., and Hammer, G. L. (2002). Tillering in grain sorghum over a wide range of population densities: identification of a common hierarchy for tiller emergence, leaf area development and fertility. Ann. Bot. 90, 87–98. doi: 10.1093/aob/mcf152

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemaire, G., Oosterom, E. V., Sheehy, J., Jeuffroy, M. H., Massignam, A., and Rossato, L. (2007). Is crop N demand more closely related to dry matter accumulation or leaf area expansion during vegetative growth? Field Crops Res. 100, 91–106. doi: 10.1016/j.fcr.2006.05.009

CrossRef Full Text | Google Scholar

Leuning, R. (1995). A critical-appraisal of a combined stomatal-photosynthesis model for c-3 plants. Plant Cell Environ. 18, 339–355. doi: 10.1111/j.1365-3040.1995.tb00370.x

CrossRef Full Text | Google Scholar

Leuning, R., Kelliher, F. M., De Pury, D. G. G., and Schulze, E. D. (1995). Leaf nitrogen, photosynthesis, conductance and transpiration: scaling from leaves to canopies. Plant Cell Environ. 18, 1183–1200. doi: 10.1111/j.1365-3040.1995.tb00628.x

CrossRef Full Text | Google Scholar

Lewis, J. D., Olszyk, D., and Tingey, D. T. (1999). Seasonal patterns of photosynthetic light response in Douglas-fir seedlings subjected to elevated atmospheric CO₂ and temperature. Tree Physiol. 19, 243–252. doi: 10.1093/treephys/19.4-5.243

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., Lin, L., Dong, Y., An, D., Li, Y., Luo, W., et al. (2012). Testing two models for the estimation of leaf stomatal conductance in four greenhouse crops cucumber, chrysanthemum, tulip and lilium. Agric. For. Meteorol. 165, 92–103. doi: 10.1016/j.agrformet.2012.06.004

CrossRef Full Text | Google Scholar

Lindquist, J. L., Arkebauer, T. J., Walters, D. T., Cassman, K. G., and Dobermann, A. (2005). Maize radiation use efficiency under optimal growth conditions. Agron. J. 97, 72–78. doi: 10.2134/agronj2005.0072

CrossRef Full Text | Google Scholar

Lobell, D. B., and Gourdji, S. M. (2012). The influence of climate change on global crop productivity. Plant Physiol. 160, 1686–1697. doi: 10.1104/pp.112.208298

PubMed Abstract | CrossRef Full Text | Google Scholar

Lobell, D. B., Hammer, G. L., Chenu, K., Zheng, B., McLean, G., and Chapman, S. C. (2015). The shifting influence of drought and heat stress for crops in northeast Australia. Global Change Biol. 21, 4115–4127. doi: 10.1111/gcb.13022

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, S. P., Marshall-Colon, A., and Zhu, X.-G. (2015). Meeting the Global Food demand of the future by engineering crop photosynthesis and yield potential. Cell 161, 56–66. doi: 10.1016/j.cell.2015.03.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, S. P., Zhu, X. G., Naidu, S. L., and Ort, D. R. (2006). Can improvement in photosynthesis increase crop yields? Plant Cell Environ. 29, 315–330. doi: 10.1111/j.1365-3040.2005.01493.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Loomis, R. S., and Williams, W. A. (1963). Maximum crop productivity: an estimate. Crop Sci. 3, 67–72. doi: 10.2135/cropsci1963.0011183X000300010021x

CrossRef Full Text | Google Scholar

López-Cedrón, F. X., Boote, K. J., Ruíz-Nogueira, B., and Sau, F. (2005). Testing CERES-Maize versions to estimate maize production in a cool environment. Eur. J. Agron. 23, 89–102. doi: 10.1016/j.eja.2005.01.001

CrossRef Full Text | Google Scholar

Marshall, B., and Biscoe, P. V. (1980). A model for C3 leaves describing the dependence of net photosynthesis on irradiance. J. Exp. Bot. 31, 29–39. doi: 10.1093/jxb/31.1.29

CrossRef Full Text | Google Scholar

Maskell, E. J. (1928). Experimental Researches on vegetable assimilation and respiration. XVIII.-the relation between stomatal opening and assimilation.-A critical study of assimilation rates and porometer rates in leaves of cherry laurel. Proc. R. Soc. Lond. Series B 102, 488–533.

Google Scholar

Massad, R.-S., Tuzet, A., and Bethenod, O. (2007). The effect of temperature on C4-type leaf photosynthesis parameters. Plant Cell Environ. 30, 1191–1204. doi: 10.1111/j.1365-3040.2007.01691.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Messina, C., Hammer, G., Dong, Z., Podlich, D., and Cooper, M. (2009). “Chapter 10 - Modelling crop improvement in a G × E × M framework via gene–trait–phenotype relationships,” in Crop Physiology, eds S. Victor and C. Daniel (San Diego, CA: Academic Press), 235–581.

Monsi, M., and Saeki, T. (1953). Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Jpn. J. Bot. 14, 22–52.

Google Scholar

Monteith, J. L. (1965a). Evaporation and environment. Symposia Soc. Exp. Biol. 19, 205–234.

PubMed Abstract | Google Scholar

Monteith, J. L. (1965b). Light distribution and photosynthesis in field crops. Ann. Bot. 29, 17–37.

Google Scholar

Monteith, J. L. (1988). Does transpiration limit the growth of vegetation or vice versa? J. Hydrol. 100, 57–68.

PubMed Abstract | Google Scholar

Monteith, J. L., and Greenwood, D. J. (1986). How do crops manipulate water supply and demand? Philos. Trans. R. Soc. Lond. A 316, 245–259. doi: 10.1098/rsta.1986.0007

CrossRef Full Text | Google Scholar

Monteith, J. L., and Moss, C. J. (1977). Climate and the efficiency of crop production in britain [and Discussion]. Philos. Trans. R. Soc. Lond. Series B Biol. Sci. 281, 277–294. doi: 10.1098/rstb.1977.0140

CrossRef Full Text

Monteith, J. L., and Unsworth, M. H. (eds.). (2013a). “Chapter 5 - radiation environment,” in Principles of Environmental Physics, 4th Edn (Boston, MA: Academic Press), 49–79.

Monteith, J. L., and Unsworth, M. H. (eds.). (2013b). “Chapter 13 - Steady-State Heat Balance: (i) Water Surfaces, Soil, and Vegetation,” in Principles of Environmental Physics, 4th Edn (Boston, MA: Academic Press), 217–247.

Google Scholar

Muchow, R. C., and Sinclair, T. R. (1994). Nitrogen response of leaf photosynthesis and canopy radiation use efficiency in field-grown maize and sorghum. Crop Sci. 34, 721–727. doi: 10.2135/cropsci1994.0011183X003400030022x

CrossRef Full Text | Google Scholar

Ogren, E. (1993). Convexity of the photosynthetic light-response curve in relation to intensity and direction of light during growth. Plant Physiol. 101, 1013–1019.

PubMed Abstract | Google Scholar

Parent, B., and Tardieu, F. (2014). Can current crop models be used in the phenotyping era for predicting the genetic variability of yield of plants subjected to drought or high temperature? J. Exp. Bot. 65, 6179–6189. doi: 10.1093/jxb/eru223

PubMed Abstract | CrossRef Full Text | Google Scholar

Parton, W. J., and Logan, J. A. (1981). A model for diurnal variation in soil and air temperature. Agric. Meteorol. 23, 205–216. doi: 10.1016/0002-1571(81)90105-9

CrossRef Full Text | Google Scholar

Pons, T. L., and de Jong-van Berkel, Y. E. M. (2004). Species-specific variation in the importance of the spectral quality gradient in canopies as a signal for photosynthetic resource partitioning. Ann. Bot. 94, 725–732. doi: 10.1093/aob/mch197

PubMed Abstract | CrossRef Full Text | Google Scholar

Pons, T. L., Flexas, J., von Caemmerer, S., Evans, J. R., Genty, B., Ribas-Carbo, M., et al. (2009). Estimating mesophyll conductance to CO₂: methodology, potential errors, and recommendations. J. Exp. Bot. 60, 2217–2234. doi: 10.1093/jxb/erp081

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabinowitch, E. I. (1951). Photosynthesis and Related Processes. New York, NY: Wiley Inter Science.

Google Scholar

Ray, D. K., Mueller, N. D., West, P. C., and Foley, J. A. (2013). Yield trends are insufficient to double global crop production by (2050). PLoS ONE 8:e66428. doi: 10.1371/journal.pone.0066428

PubMed Abstract | CrossRef Full Text | Google Scholar

Roupsard, O., Dauzat, J., Nouvellon, Y., Deveau, A., Feintrenie, L., Saint-André, L., et al. (2008). Cross-validating Sun-shade and 3D models of light absorption by a tree-crop canopy. Agric. Forest Meteorol. 148, 549–564. doi: 10.1016/j.agrformet.2007.11.002

CrossRef Full Text | Google Scholar

Sadras, V. O., and Lawson, C. (2011). Genetic gain in yield and associated changes in phenotype, trait plasticity and competitive ability of South Australian wheat varieties released between 1958 and (2007). Crop Pasture Sci. 62, 533–549. doi: 10.1071/CP11060

CrossRef Full Text | Google Scholar

Saeki, T. (1960). Interrelationships between leaf amount, light distribution and total photosynthesis in a plant community. Shokubutsugaku Zasshi 73, 55–63. doi: 10.15281/jplantres1887.73.55

CrossRef Full Text

Sage, R. F., and Kubien, D. S. (2007). The temperature response of C3 and C4 photosynthesis. Plant Cell Environ. 30, 1086–1106. doi: 10.1111/j.1365-3040.2007.01682.x

PubMed Abstract | CrossRef Full Text

Sellers, P. J., Berry, J. A., Collatz, G. J., Field, C. B., and Hall, F. G. (1992). Canopy reflectance, photosynthesis, and transpiration.3. A reanalysis using improved leaf models and a new canopy integration scheme. Remote Sens. Environ. 42, 187–216. doi: 10.1016/0034-4257(92)90102-P

CrossRef Full Text | Google Scholar

Sharwood, R. E., and Whitney, S. M. (2014). Correlating Rubisco catalytic and sequence diversity within C3 plants with changes in atmospheric CO₂ concentrations. Plant Cell Environ. 37, 1981–1984. doi: 10.1111/pce.12386

PubMed Abstract | CrossRef Full Text | Google Scholar

Shibles, R. M., and Weber, C. R. (1965). Leaf area, solar radiation interceptionand dry matter production by soybeans. Crop Sci. 5, 3. doi: 10.2135/cropsci1965.0011183X000500060027x

CrossRef Full Text | Google Scholar

Shibles, R. M., and Weber, C. R. (1966). Interception of Solar Radiation and dry matter production by various soybean planting Patterns1. Crop Sci. 6, 55–59. doi: 10.2135/cropsci1966.0011183X000600010017x

CrossRef Full Text | Google Scholar

Sinclair, T. R. (1986). Water and nitrogen limitations in soybean grain production I. model development. Field Crops Res. 15, 125–141. doi: 10.1016/0378-4290(86)90082-1

CrossRef Full Text | Google Scholar

Sinclair, T. R., and Horie, T. (1989). Leaf nitrogen, photosynthesis, and crop radiation use efficiency - a review. Crop Sci. 29, 90–98. doi: 10.2135/cropsci1989.0011183X002900010023x

CrossRef Full Text | Google Scholar

Sinclair, T. R., and Muchow, R. C. (1999). Radiation use efficiency. Adv. Agron. 65, 215–265. doi: 10.1016/S0065-2113(08)60914-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinclair, T. R., Murphy, C. E., and Knoerr, K. R. (1976). Development and evaluation of simplified models for simulating canopy photosynthesis and transpiration. J. Appl. Ecol. 13, 813–829. doi: 10.2307/2402257

CrossRef Full Text | Google Scholar

Sinclair, T. R., Purcell, L. C., and Sneller, C. H. (2004). Crop transformation and the challenge to increase yield potential. Trends Plant Sci. 9, 70–75. doi: 10.1016/j.tplants.2003.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinclair, T. R., Shiraiwa, T., and Hammer, G. L. (1992). Variation in crop radiation-use efficiency with increased diffuse-radiation. Crop Sci. 32, 1281–1284. doi: 10.2135/cropsci1992.0011183X003200050043x

CrossRef Full Text | Google Scholar

Singh, V., van Oosterom, E. J., Jordan, D. R., and Hammer, G. L. (2012). Genetic control of nodal root angle in sorghum and its implications on water extraction. Eur. J. Agron. 42, 3–10. doi: 10.1016/j.eja.2012.04.006

CrossRef Full Text | Google Scholar

Sinoquet, H., Le Roux, X., Adam, B., Ameglio, T., and Daudet, F. A. (2001). RATP: a model for simulating the spatial distribution of radiation absorption, transpiration and photosynthesis within canopies: application to an isolated tree crown. Plant Cell Environ. 24, 395–406. doi: 10.1046/j.1365-3040.2001.00694.x

CrossRef Full Text | Google Scholar

Song, Q., Zhang, G., and Zhu, X.-G. (2013). Optimal crop canopy architecture to maximise canopy photosynthetic CO₂ uptake under elevated CO₂ – a theoretical study using a mechanistic model of canopy photosynthesis. Funct. Plant Biol. 40, 108–124. doi: 10.1071/FP12056

CrossRef Full Text | Google Scholar

Tahiri, A. Z., Anyoji, H., and Yasuda, H. (2006). Fixed and variable light extinction coefficients for estimating plant transpiration and soil evaporation under irrigated maize. Agric. Water Manag. 84, 186–192. doi: 10.1016/j.agwat.2006.02.002

CrossRef Full Text | Google Scholar

Tardieu, F., Simonneau, T., and Parent, B. (2015). Modelling the coordination of the controls of stomatal aperture, transpiration, leaf growth, and abscisic acid: update and extension of the Tardieu–Davies model. J. Exp. Bot. 66, 2227–2237. doi: 10.1093/jxb/erv039

PubMed Abstract | CrossRef Full Text | Google Scholar

Terashima, I., Hanba, Y. T., Tholen, D., and Niinemets, Ü. (2011). Leaf functional anatomy in relation to photosynthesis. Plant Physiol. 155, 108–116. doi: 10.1104/pp.110.165472

PubMed Abstract | CrossRef Full Text | Google Scholar

Thornley, J. H. M. (1976). Mathematical Models in Plant Physiology. London: Academic Press.

Thornley, J. H. M. (1998). Dynamic model of leaf photosynthesis with acclimation to light and nitrogen. Ann. Bot. 81, 421–430. doi: 10.1006/anbo.1997.0575

CrossRef Full Text | Google Scholar

Thornley, J. H. M. (2002). Instantaneous canopy photosynthesis: analytical expressions for sun and shade leaves based on exponential light decay down the canopy and an acclimated non-rectangular hyperbola for leaf photosynthesis. Ann. Bot. 89, 451–458. doi: 10.1093/aob/mcf071

PubMed Abstract | CrossRef Full Text | Google Scholar

Tollenaar, M., and Lee, E. A. (2006). Dissection of physiological processes underlying grain yield in maize by examining genetic improvement and heterosis. Maydica 51, 399–408.

Google Scholar

Tomás, M., Flexas, J., Copolovici, L., Galmés, J., Hallik, L., Medrano, H., et al. (2013). Importance of leaf anatomy in determining mesophyll diffusion conductance to CO(2) across species: quantitative limitations and scaling up by models. J. Exp. Bot. 64, 2269–2281. doi: 10.1093/jxb/ert086

PubMed Abstract | CrossRef Full Text | Google Scholar

van Oosterom, E. J., Borrell, A. K., Chapman, S. C., Broad, I. J., and Hammer, G. L. (2010). Functional dynamics of the nitrogen balance of sorghum: I. N demand of vegetative plant parts. Field Crops Res. 115, 19–28. doi: 10.1016/j.fcr.2009.09.018

CrossRef Full Text | Google Scholar

van Oosterom, E. J., O'Leary, G. J., Carberry, P. S., and Craufurd, P. Q. (2002). Simulating growth, development, and yield of tillering pearl millet. III. Biomass accumulation and partitioning. Field Crops Res. 79, 85–106. doi: 10.1016/S0378-4290(02)00156-9

CrossRef Full Text | Google Scholar

von Caemmerer, S. (2000). Biochemical Models of Leaf Photosynthesis, Vol. 2. Collingwood, ON: CSIRO Publishing.

von Caemmerer, S. (2013). Steady-state models of photosynthesis. Plant Cell Environ. 36, 1617–1630. doi: 10.1111/pce.12098

PubMed Abstract | CrossRef Full Text | Google Scholar

von Caemmerer, S., and Farquhar, G. D. (1981). Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves. Planta 153, 376–387. doi: 10.1007/BF00384257

PubMed Abstract | CrossRef Full Text | Google Scholar

von Caemmerer, S., and Furbank, R. T. (1999). “6 - modeling C4 photosynthesis,” in C4 Plant Biology, ed R. F. S. K. Monson (San Diego, CA: Academic Press), 173–211.

von Caemmerer, S., Farquhar, G., and Berry, J. (2009). “Biochemical model of C3 photosynthesis,” in Photosynthesis in silico: Understanding Complexity from Molecules to Ecosystems, eds A. Laisk, L. Nedbal, and Govindjee (Dordrecht: Springer), 209–230.

Vos, J., Evers, J. B., Buck-Sorlin, G. H., Andrieu, B., Chelle, M., and de Visser, P. H. B. (2010). Functional-structural plant modelling: a new versatile tool in crop science. J. Exp. Bot. 61, 2101–2115. doi: 10.1093/jxb/erp345

PubMed Abstract | CrossRef Full Text

Walker, B., Ariza, L. S., Kaines, S., Badger, M. R., and Cousins, A. B. (2013). Temperature response of in vivo Rubisco kinetics and mesophyll conductance in Arabidopsis thaliana: comparisons to Nicotiana tabacum. Plant Cell Environ. 36, 2108–2119. doi: 10.1111/pce.12166

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y. P., and Leuning, R. (1998). A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I: model description and comparison with a multi-layered model. Agric. For. Meteorol. 91, 89–111. doi: 10.1016/S0168-1923(98)00061-6

CrossRef Full Text | Google Scholar

Whitney, S. M., Houtz, R. L., and Alonso, H. (2011). Advancing our understanding and capacity to engineer nature's CO₂-sequestering enzyme, Rubisco. Plant Physiol. 155, 27–35. doi: 10.1104/pp.110.164814

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, W. A., Loomis, R. S., and Leplcy, C. R. (1965). Vegetative growth of corn as affected by population density: I. Productivity in relation to interception of solar radiation. Crop Sci. 5, 5.

Xu, J. Z., Yu, Y. M., Peng, S. Z., Yang, S. H., and Liao, L. X. (2014). A modified nonrectangular hyperbola equation for photosynthetic light-response curves of leaves with different nitrogen status. Photosynthetica 52, 117–123. doi: 10.1007/s11099-014-0011-3

CrossRef Full Text | Google Scholar

Yang, Y., Kim, S. H., Timlin, D. J., Fleisher, D. H., Quebedeaux, B., and Reddy, V. R. (2009). Simulating canopy transpiration and photosynthesis of corn plants under contrasting water regimes using a coupled model. Trans. ASABE 52, 1011–1024. doi: 10.13031/2013.27370

CrossRef Full Text | Google Scholar

Ye, Z. P. (2007). A new model for relationship between irradiance and the rate of photosynthesis in Oryza sativa. Photosynthetica 45, 637–640. doi: 10.1007/s11099-007-0110-5

CrossRef Full Text | Google Scholar

Ye, Z.-P., Suggett, D. J., Robakowski, P., and Kang, H.-J. (2013). A mechanistic model for the photosynthesis–light response based on the photosynthetic electron transport of photosystem II in C3 and C4 species. New Phytol. 199, 110–120. doi: 10.1111/nph.12242

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, X., and Struik, P. C. (2008). Applying modelling experiences from the past to shape crop systems biology: the need to converge crop physiology and functional genomics. New Phytol. 179, 629–642. doi: 10.1111/j.1469-8137.2008.02424.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, X., and Struik, P. C. (2009). C-3 and C-4 photosynthesis models: an overview from the perspective of crop modelling. Njas Wageningen J. Life Sci. 57, 27–38. doi: 10.1016/j.njas.2009.07.001

CrossRef Full Text | Google Scholar

Yin, X., and Struik, P. C. (2015). Constraints to the potential efficiency of converting solar radiation into phytoenergy in annual crops: from leaf biochemistry to canopy physiology and crop ecology. J. Exp. Bot. 66, 6535–6549. doi: 10.1093/jxb/erv371

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, X., and van Laar, H. H. (2005). Crop Systems Dynamics: An Ecophysiological Simulation Model for Genotype-by-Environment Interactions. Wageningen: Wageningen Academic Publishers.

Google Scholar

Yin, X., Harbinson, J., and Struik, P. C. (2009). “A model of the generalized stoichiometry of electron transport limited C3 photosynthesis: development and applications,” in Photosynthesis in silico: Understanding Complexity from Molecules to Ecosystems, eds A. Laisk, L. Nedbal, and Govindjee (Dordrecht: Springer), 247–273.

Yin, X., van der Putten, P. E. L., Driever, S. M., and Struik, P. C. (2016). Temperature response of bundle-sheath conductance in maize leaves. J. Exp. Bot. 67, 2699–2714. doi: 10.1093/jxb/erw104

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, X., Van Oijen, M., and Schapendonk, A. H. C. M. (2004). Extension of a biochemical model for the generalized stoichiometry of electron transport limited C3 photosynthesis. Plant Cell Environ. 27, 1211–1222. doi: 10.1111/j.1365-3040.2004.01224.x

CrossRef Full Text | Google Scholar

Zhu, X. G., Long, S. P., and Ort, D. R. (2010). Improving photosynthetic efficiency for greater yield. Annu. Rev. Plant Biol. 61, 235–261. doi: 10.1146/annurev-arplant-042809-112206

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X. G., Portis, A. R., and Long, S. P. (2004). Would transformation of C-3 crop plants with foreign Rubisco increase productivity? A computational analysis extrapolating from kinetic properties to canopy photosynthesis. Plant Cell Environ. 27, 155–165. doi: 10.1046/j.1365-3040.2004.01142.x

CrossRef Full Text | Google Scholar