Combining Genome-Wide Information with a Functional Structural Plant Model to Simulate 1-Year-Old Apple Tree Architecture

In crops, optimizing target traits in breeding programs can be fostered by selecting appropriate combinations of architectural traits which determine light interception and carbon acquisition. In apple tree, architectural traits were observed to be under genetic control. However, architectural traits also result from many organogenetic and morphological processes interacting with the environment. The present study aimed at combining a FSPM built for apple tree, MAppleT, with genetic determinisms of architectural traits, previously described in a bi-parental population. We focused on parameters related to organogenesis (phyllochron and immediate branching) and morphogenesis processes (internode length and leaf area) during the first year of tree growth. Two independent datasets collected in 2004 and 2007 on 116 genotypes, issued from a ‘Starkrimson’ × ‘Granny Smith’ cross, were used. The phyllochron was estimated as a function of thermal time and sylleptic branching was modeled subsequently depending on phyllochron. From a genetic map built with SNPs, marker effects were estimated on four MAppleT parameters with rrBLUP, using 2007 data. These effects were then considered in MAppleT to simulate tree development in the two climatic conditions. The genome wide prediction model gave consistent estimations of parameter values with correlation coefficients between observed values and estimated values from SNP markers ranging from 0.79 to 0.96. However, the accuracy of the prediction model following cross validation schemas was lower. Three integrative traits (the number of leaves, trunk length, and number of sylleptic laterals) were considered for validating MAppleT simulations. In 2007 climatic conditions, simulated values were close to observations, highlighting the correct simulation of genetic variability. However, in 2004 conditions which were not used for model calibration, the simulations differed from observations. This study demonstrates the possibility of integrating genome-based information in a FSPM for a perennial fruit tree. It also showed that further improvements are required for improving the prediction ability. Especially temperature effect should be extended and other factors taken into account for modeling GxE interactions. Improvements could also be expected by considering larger populations and by testing other genome wide prediction models. Despite these limitations, this study opens new possibilities for supporting plant breeding by in silico evaluations of the impact of genotypic polymorphisms on plant integrative phenotypes.

Introduction

Tree architecture plays a key role in collecting light and assimilating carbon and thus affects plant growth and yield (Valladares et al., 2002; Niinemets, 2010). Moreover, by modifying plant microclimate, it also determines many characteristics of fruit quality and can affect the development of orchard pests and diseases (Lauri and Costes, 2009). Previous studies have demonstrated that, across vascular plants, architecture exhibits remarkable regularities (Hallé et al., 1978; Sussex and Kerk, 2001) which are assumed to result from genetic control (Reinhardt and Kuhlemeier, 2002). Even though genetics and breeding aim at selecting optimal combinations of traits (a genotype with such optimal characteristics being considered as an ideotype; Donald, 1968), the optimization of plant architecture is not straightforward because it results from many morphological and physiological processes interacting with the environment. In addition, defining an ideotype for a given species and for particular environmental or agronomic conditions can be extremely time- and resource consuming especially in perennials which characteristics may change over years. Modeling appears as an appropriate tool for the prediction and simulation of tree architecture and related properties in order to explore possible ideotypes.

Functional-structural plant models (FSPM) have been developed for analyzing the relationships between plant architecture, light interception, microclimate, and physiological processes such as carbon assimilation or water losses by transpiration (Vos et al., 2010; DeJong et al., 2011). These models combine a 3D representation of plant architecture with mathematical formalisms describing physiological functions (photosynthesis, carbon allocation…) at different scales of plant organization (from organs to plant). This kind of models has been developed for different annual (e.g., Fournier et al., 2003; Evers et al., 2007), or perennial crops (e.g., Perttunen et al., 1998; Allen et al., 2005; Costes et al., 2008). Most of them have been calibrated and validated on one or a few genotypes with contrasting architectures. However, there is strong evidence that components and processes responsible for plant architecture are highly heritable and under genetic control (Wu and Stettler, 1994; Wu, 1998; De Wit et al., 2002; Perez et al., 2016). This opened new perspectives for integrating architectural traits in breeding programs (Wu, 1998; Rötter et al., 2015).

Previous studies have included the genetic variability in FSPMs by estimating physiological or morphological parameters using QTL information (Letort et al., 2008; Xu et al., 2012). More precisely, QTL effects have been used to predict the values of some FSPM input parameters such as those determining organ sing strength. QTL effects have been estimated on virtual recombinant populations (Letort et al., 2008). However, these methods could be applied if QTLs are detected for model parameters whereas architectural traits revealed high polygenic determinisms (Wu and Stettler, 1994; Segura et al., 2008). Concomitantly, the development of high density genetic maps with single nucleotide polymorphism (SNP) markers have allowed the emergence of genome wide prediction models which aims at predicting genotypic values based on whole genome information (Heffner et al., 2009; Kumar et al., 2012). The statistical challenge of the genome wide prediction models is to estimate in a regression model the effects of a number of markers larger than the number of individuals, this leading to over-fitting problems. Statistical methods have been developed to reduce the risk of over-fitting (de los Campos et al., 2013) by applying a selection of variables and/or a shrinkage parameter on marker effects. Genome wide prediction models used a mixed model approach and marker effects are estimated according to a prior distribution. This prior distribution can be a Gaussian distribution in the Ridge Regression BLUP method (Endelman, 2011), a double exponential or t distributions in Bayesian approaches (de los Campos et al., 2013).

The aim of the present study was to combine a FSPM previously built for apple tree (MAppleT, Costes et al., 2008) with genetic determinisms of architectural traits in a bi-parental segregating population. This population has been previously studied and showed a strong heritability of architectural traits (Segura et al., 2006, 2008). Our objective was to explore the feasibility of combining the effects of SNP markers on model parameters related to architectural traits with MAppleT in order to simulate tree architecture.

MAppleT simulates apple tree above-ground development over years (Costes et al., 2008), by combining Markovian models to simulate the dynamic of tree topology and a bio-mechanical model to simulate the geometry (branch angle and bending; Jirasek et al., 2000; Alméras et al., 2002). Presently, MAppleT does not simulate any environmental effect on growth processes and does not include the simulation of carbon source-sink relationships or water fluxes within the tree. Primary growth is modeled based on the phyllochron (time between the appearance of two consecutive leaves) which is considered as a constant value and the final size of organs (internode, leaf) is an input parameter of the model. Previous studies showed that changing the values of these architectural traits in MAppleT, considering the range of values observed in the segregating population mentioned above, modifies the light interception of the simulated trees (Da Silva et al., 2014).

We focused on the vegetative development during the first year of apple tree growth which is a critical period for architecture establishment. During this initial growth period, apple tree develops a main stem with immediate laterals (or sylleptic; Segura et al., 2006). Therefore, the main variables of interest for simulating primary growth and branching at this stage are the phyllochron, the internode length, the individual leaf area, and the probability of appearance of the sylleptic laterals along the main stem. Some relations between these variables have been observed. Notably, the phyllochron is assumed to modulate sylleptic branching since the number of sylleptic laterals is often higher when the phyllochron is low during the season (Remphrey and Powell, 1985; Powell, 1991; Génard et al., 1994). Moreover, temperature affects the phyllochron of some fruit species such as kiwifruit or grapevine (Morgan et al., 1985; Pallas et al., 2008). For peach tree, the phyllochron could be modeled as a function of thermal time (TT; Kervella et al., 1995; Lescourret et al., 1998) even if temperature was not the only factor influencing the phyllochron when trees are grown in open field conditions (Davidson et al., 2015).

In this study, we simulated 1-year-old apple tree architectures depending on the genotype and air temperature over a growing season. This approach was built through four sub-objectives: (i) modeling the dynamic of phytomer emergence and the subsequent sylleptic branching depending on TT, (ii) estimating key MAppleT parameters based on SNP marker effects, (iii) integrating the environmental and the marker effects in MAppleT to simulate genotype development based on genetic and climatic information, (iv) validate the method by comparing simulation outputs with observed data.

Materials and Methods

Plant Material, Phenotyping, and Genotyping

The study was carried out on 116 genotypes corresponding to an apple tree (Malus × Domestica) F1 progeny issued from a “Starkrimson” × “Granny Smith” cross. The parents were selected for their contrasted architecture and bearing behavior. Indeed, the ‘Starkrimson’ maternal parent displays an erect growth habit with many short shoots and a tendency to irregular bearing (Lespinasse, 1992). Conversely, the ‘Granny Smith’ pollen parent displays a weeping habit with long shoots and fruit-bearing regularity (Segura et al., 2007, 2008).

Two field experiments were planted in 2007 (Experiment 1) and 2004 (Experiment 2) at the Melgueil INRA Montpellier experimental station (France, 43°36′N 3°58′E). In both experiments, two replicates of each genotype were grafted on Pajam 1 rootstock and planted 5 m × 1.5 m apart in a north-south orientation. Throughout the experiments, the 232 trees were well-watered and not pruned.

In each experiment, the topology of each tree was described as explained in Segura et al. (2006) at the end of the first growth season and recorded in Multiscale Tree Graph format (MTG, Godin and Caraglio, 1998). The trunk length, the mean internode length on the trunk, the number of sylleptic laterals, and their position along the trunk were extracted from the MTG. In Experiment 1, the number of newly emerged leaves on trunk was also counted weekly, from July to the end of growth in September (11 dates of measurement). When trees were 3-year-old in Experiment 1, the maximal individual leaf areas along four randomly chosen shoots were measured on each tree at the end of the growing season (end of September 2009). This maximal leaf area has been already observed to be highly heritable and to display lower variability than individual leaf areas along the trunk (Lopez et al., 2015).

The population was genotyped with the Infinium^® 20K SNP array (Bianco et al., 2014) at the Fondazione Edmund Mach according to the procedures described by Antanaviciute et al. (2012) and Chagné et al. (2012). Among the 6849 polymorphic SNPs, 3123 were used in this study, after a careful checking of their robustness consistency (Van de Weg et al., 2013; Di Guardo et al., 2015) and recombination pattern (Allard et al., 2016). In particular, all markers which were not strictly bi-allelic in at least one of the parent were discarded. We removed these markers because there were not informative to evaluate genetic effects in quantitative genetic studies. Indeed, in that case, all the individuals of the progeny had the same alleles at these markers.

Modeling Temperature Impact on Leaf Emergence Rate and Sylleptic Branching

Nine linear mixed models (see Supplementary Material 1.1) were compared to analyze the effect of temperature on the daily rate of leaf emergence (RLE) and its genetic variability depending on temperature. Since we did not want to increase the number of parameters in the MAppleT, the BIC was chosen for model selection because it is known to be more adequate for selecting models with a few number of parameters compared to the AIC (Davidson and Mackinnon, 2004). The two first models did not include temperature effect and assumed a constant RLE throughout the growing season. Two different methods were used to calculate TT based on either the daily mean temperature (T_Mean) or a single sine method (T_SSM) using 7 and 35°C as lower and upper threshold as in Lescourret et al. (1998) on peach tree. In the subsequent analyzes, the RLE was expressed in growing degree-day (RLE_GDD) and computed as the slope of the relationship between TT using T_SSM and the number of emitted leaves.

To account for the relationship between the parent shoot growth and the appearance of sylleptic lateral at a given node, each day the probability of producing a sylleptic lateral, noted P_d, was assumed to be linearly dependent on the RLE. In this study and according to Peyhardi et al. (2013), we considered the values of RLE during the n_days days before leaf emergence of the considered metamer on which sylleptic lateral development can occur. Moreover, we assumed that a sylleptic lateral only appears at a given rank (called r_k) below the terminal apex, in order to represent the inhibition of axillary bud outgrowth by the apical meristem (Cline, 2000; Beveridge, 2006). In the model, the probability of sylleptic lateral emergence was computed when a new leaf was emitted by the terminal apex. The probability of appearance of a sylleptic lateral at a node of rank k - r_k and at day d was thus expressed as follows:

${\mathit{P}}_{\mathit{d}}\mathrm{(}\mathit{S}\mathit{y}\mathit{l}\mathit{l}\mathit{e}\mathit{p}\mathit{t}\mathit{i}\mathit{c}\mathit{}\mathit{b}\mathit{r}\mathit{a}\mathit{n}\mathit{c}\mathit{h}\mathit{i}\mathit{n}\mathit{g}\mathrm{}\mathrm{(}\mathit{k}\mathit{-}{\mathit{r}}_{\mathit{k}}\mathrm{)}\mathrm{|}\mathit{P}\mathit{h}\mathit{y}\mathit{t}\mathit{o}\mathit{m}\mathit{e}\mathit{r}\mathit{}\mathit{c}\mathit{r}\mathit{e}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathrm{}\mathrm{\left(}\mathit{k}\mathrm{\right)}\mathrm{)}\mathrm{=}{\mathit{a}}_{\mathit{s}\mathit{y}\mathit{l}\mathit{l}}\mathrm{\times }\frac{\mathrm{1}}{{\mathit{n}}_{\mathit{d}\mathit{a}\mathit{y}\mathit{s}}}\underset{\mathit{i}\mathit{=}{\mathit{d}\mathit{-}\mathit{n}}_{\mathit{d}\mathit{a}\mathit{y}\mathit{s}}}{\overset{\mathit{d}}{\mathrm{\Sigma }}}{\mathit{R}\mathit{L}\mathit{E}}_{\mathit{i}}\mathrm{}\mathrm{\left(}\mathrm{1}\mathrm{\right)}$

where a_syll is the coefficient of the linear relation between P_d and the mean value of RLE during the n_days previous days.

The values of r_k and n_days were determined with a virtual experiment in which tree development was simulated with MAppleT using different values, 5, 10, 15, and 20 for r_k and 3, 7, and 10 for n_days, respectively (see Supplementary Figure 1). The best combination of parameters (20 LD and 7 n_days) was defined as the combination which minimizes the root mean squared error (RMSE) between observed and simulated distributions of sylleptic laterals along the trunk. r_k and n_days were estimated on the mean distribution of sylleptic laterals considering all genotypes together. Indeed, since sylleptic branching is a rare event, the number of replicates (only two) was not enough to get a consistent representation of the distribution of sylleptic laterals along the trunk for each genotype of the population. Values of r_k and n_days were thus considered as identical for each genotype.

FIGURE 1

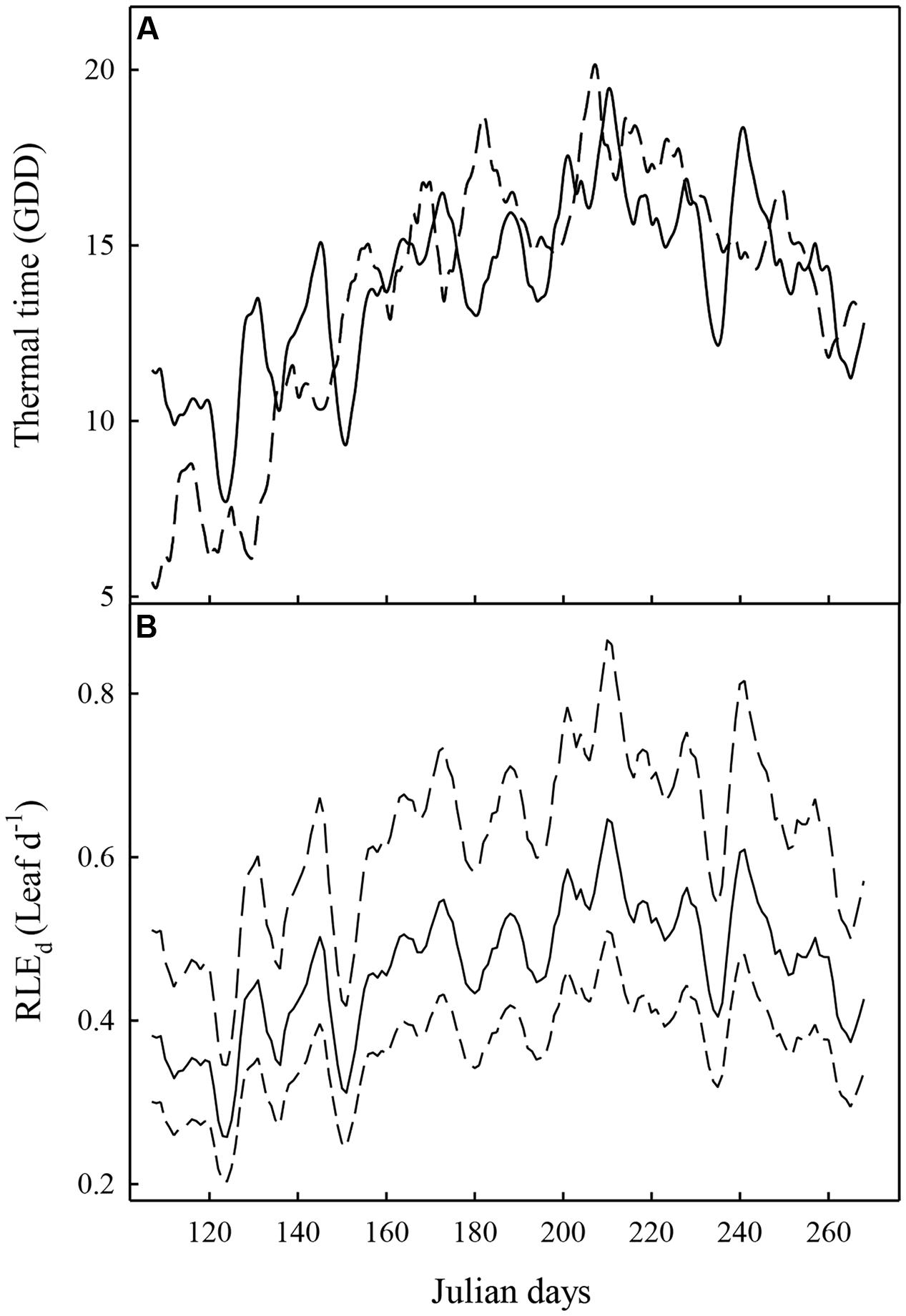
FIGURE 1. Evolution of the thermal time (A) and the rate of leaf emergence per day (RLE_d) (B) averaged over 5 days (from 2 days before to 2 days after each day in abscissa), the two experiments (Experiment 1: full line; Experiment 2: dashed line). In (B), the mean value of RLE_d on the 116 hybrids is represented with a full line. The dashed lines represent the maximum and minimum RLE_d values recorded on the population.

Estimation of MAppleT Parameter Values

We focused on four parameters used in MAppleT, (i) RLE_GDD, (ii) the length of individual internode (IN_length), (iii) the area of individual leaf (Leaf_area), and (iv) a_syll. In MAppleT, these parameters are the main parameters driving primary growth and branching. The other parameters that can affect primary tree growth in MAppleT are the parameters related to the dynamics of organ expansion but we did not consider them in this study because they had no impact on the final architecture (all the organs end their growth at the end of the growth season) and because they are difficult to estimate experimentally on a large range on genotypes.

Values of these four parameters were estimated on each tree in Experiment 1. IN_length was the mean internode length recorded at the end of the experiment. Leaf_area was estimated as the mean leaf area of the four leaves measured at the end of Experiment 1. These dimensions were then considered in MAppleT as the final dimensions of internodes and leaves for all the metamers along the trunk and branches expect for the preformed metamers (eight first leaves). In MAppleT, organ expansion is modeled as a logistic growth functions and the value of this function reaches Leaf_area or IN_Length at the end of the organ growth period (Da Silva et al., 2014).

The value of a_syll was estimated for each tree as a function of the total number of sylleptic laterals (N_syll), the RLE_GDD and the sum of the daily thermal time (TT_d) during the growing season (15 April–30 September; see more information in Supplementary Material 1.2), as follows:

${\mathit{a}}_{\mathit{s}\mathit{y}\mathit{l}\mathit{l}}\mathit{=}\frac{{\mathit{N}}_{\mathit{s}\mathit{y}\mathit{l}\mathit{l}}}{{\mathrm{\left(}{\mathit{R}\mathit{L}\mathit{E}}_{\mathit{G}\mathit{D}\mathit{D}}\mathrm{\right)}}^{\mathrm{2}}\mathit{\times }{\mathit{\Sigma }}_{\mathit{d}}^{{\mathit{d}}_{\mathit{e}}}\mathit{=}{\mathit{d}}_{\mathit{b}}\mathrm{(}\frac{\mathrm{1}}{{\mathit{n}}_{\mathit{d}\mathit{a}\mathit{y}\mathit{s}}}{\mathrm{\Sigma }}_{\mathit{i}}^{\mathit{d}}\mathit{=}{\mathit{d}\mathit{-}\mathit{n}}_{\mathit{d}\mathit{a}\mathit{y}\mathit{s}}{\mathit{T}\mathit{T}}_{\mathit{i}}\mathrm{)}\mathit{\times }{\mathit{T}\mathit{T}}_{\mathit{d}}}\mathit{}\mathrm{\left(}\mathrm{2}\mathrm{\right)}$

where d_b is the day when the node of rank r_k appears on tree, d_e is the day of the end of growing season.

The value of RLE_GDD for each individual was estimated from the linear model between RLE and TT that minimized the BIC (see Supplementary Table 1).

TABLE 1

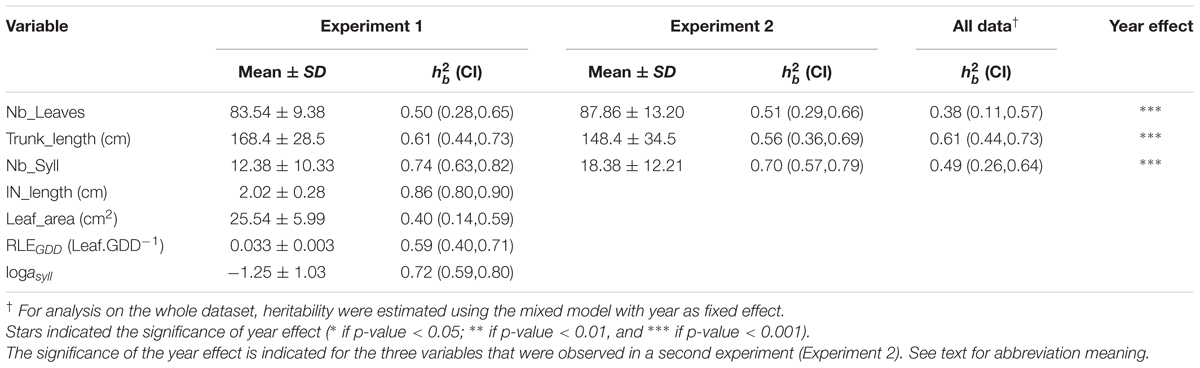
TABLE 1. Mean value, standard deviation, mean heritability value (${\mathit{h}}_{\mathit{b}}^{\mathrm{2}}$) with confidence interval (CI) indicated in brackets for five measured variables (Nb_Leaves, Trunk_length, Nb_Syll, IN_length, and Leaf_area) and two estimated model parameters (RLE_GDD, loga_syll) on trunks of 116 1-year-old hybrid apple trees, in experiment 1.

Analyses of the Genetic Variability, Correlations, and Heritability Values of MAppleT Parameters and Architectural Variables

Analyses of genetic variability and heritability were performed on the four MAppleT parameters and on three architectural traits directly measured on trees: the length of trunk (Trunk_length), the total number of leaves (Nb_Leaves), and the number of sylleptic laterals (Nb_syll). Moreover, as a_syll distribution was not Gaussian, its logarithm, called loga_syll, which was normally distributed, was used for the genetic analyses.

The significance of the genotypic effect on the four parameters and on the three integrative variables was estimated, for both experiments separately, using a linear mixed model with genotype as random effect as follows:

${\mathit{P}}_{\mathit{i}\mathit{j}}\mathit{=}\mathrm{\mu }\mathit{+}{\mathit{G}}_{\mathit{i}}\mathit{+}{\mathit{e}}_{\mathit{i}\mathit{j}}\mathit{}\mathrm{\left(}\mathrm{3}\mathrm{\right)}$

where P_ij is the phenotype value of the j^th replicate of genotype i, μ is the overall mean of the progeny, G_i is the random effect of the genotype i, and e_ij is the gaussian residual. This model was fitted on data using the lmer procedure of the lme4 package of R software. The mean broad-sense heritability was calculated as:

${\mathit{h}}_{\mathit{b}}^{\mathrm{2}}\mathit{=}\frac{{\mathit{\sigma }}_{\mathit{G}}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathit{G}}^{\mathrm{2}}\mathit{+}\frac{{\mathit{\sigma }}_{\mathit{e}}^{\mathrm{2}}}{\mathit{n}}}\mathrm{\left(}\mathrm{4}\mathrm{\right)}$

where ${\mathrm{\sigma }}_{\mathit{G}}^{\mathrm{2}}$ is the genotypic variance, ${\mathrm{\sigma }}_{\mathit{e}}^{\mathrm{2}}$ is the residual variance, and n is the number of replicates per genotype. In order to analyze the genetic variability on the two experiments together, the following linear mixed model using years as fixed effect and genotype as random effect was used.

${\mathit{P}}_{\mathit{i}\mathit{j}\mathit{k}}\mathit{=}\mathrm{\mu }\mathit{+}{\mathit{A}}_{\mathit{i}}\mathit{+}{\mathit{G}}_{\mathit{j}}\mathit{+}{\mathit{I}}_{\mathit{i}\mathit{j}}\mathit{+}{\mathit{e}}_{\mathit{i}\mathit{j}\mathit{k}}\mathrm{\left(}\mathrm{5}\mathrm{\right)}$

where P_ijk is the phenotype value of the k^th replicate of genotype j in the year i, μ is the overall mean of the progeny over the 2 years, A_i is the fixed effect of the year i, G_j is the random effect of the genotype j, I_ij is the random effect of the interaction between the effects of the year i and the genotype j and e_ijk is the gaussian residual. The mean broad-sense heritability over the 2 years was calculated for the whole data as:

${\mathit{h}}_{\mathit{b}}^{\mathrm{2}}\mathit{=}\frac{{\mathrm{\sigma }}_{\mathit{G}}^{\mathrm{2}}}{{\mathrm{\sigma }}_{\mathit{G}}^{\mathrm{2}}\mathit{+}\mathit{\left(}\frac{{\mathrm{\sigma }}_{\mathit{i}}^{\mathrm{2}}}{\mathit{a}}\mathit{\right)}\mathit{+}\mathit{\left(}\frac{{\mathrm{\sigma }}_{\mathit{e}}^{\mathrm{2}}}{\mathit{n}\mathit{\times }\mathit{a}}\mathit{\right)}}\mathit{}\mathrm{\left(}\mathrm{6}\mathrm{\right)}$

where ${\mathrm{\sigma }}_{\mathit{G}}^{\mathrm{2}}$ is the genotypic variance, ${\mathrm{\sigma }}_{\mathit{I}}^{\mathrm{2}}$ is the interaction variance, ${\mathrm{\sigma }}_{\mathit{e}}^{\mathrm{2}}$ is the residual variance, a is the number of years, and n is the number of replicates. The significance of the year effect was evaluated using anova procedure of the lmerTest package of R software.

For each heritability value, associated confidence intervals were calculated as defined in Knapp et al. (1985). The phenotypic and genotypic correlations between MAppleT parameters and architectural traits were calculated for each experiment separately. Correlations between the two experimental dataset were calculated for the three architectural traits, only. The significance of the correlations was tested with a Pearson’s test.

Genomic Prediction of MAppleT Parameter Values

Following Xu et al. (2011), QTL were detected on BLUPs for the four studied parameters using the interval mapping method within the MapQTL software (Van Ooijen et al., 2002). The logarithm of the odds (LOD) at which QTL was declared significant was determined according to a genome wide error of 0.05 over 2000 permutations of the data. A QTL was considered as significant when the associated LOD was higher than 4.

As polygenic determinisms were expected, a genomic prediction method based on Ridge Regression was used after this QTL analysis (Whittaker et al., 2000; Meuwissen et al., 2001). More precisely, this method estimates infinitesimal loci effects assuming a shrinkage parameter equals to the ratio of the residual to the environmental variance using the following mixed effect model:

$\mathit{Y}\mathit{=}\mathrm{\mu }\mathit{+}{\mathit{X}}_{\mathit{g}}\mathit{+}\mathit{e}\mathrm{\left(}\mathrm{7}\mathrm{\right)}$

where Y are the phenotypic values (232 × 1; two replicates per genotype), μ is the overall mean of phenotypic value, X (232 × 2160) is the matrix of markers for each individual, g (2160 × 1) is the marker effects which are assumed to be normally distributed $\mathrm{(}\mathit{g}\mathrm{\sim }\mathit{N}\mathrm{(}\mathrm{0}\mathrm{,}\mathit{I}{\mathrm{\sigma }}_{\mathit{g}}^{\mathrm{2}}\mathrm{)}\mathrm{)}$, and e (232 × 1) is the residual effects $\mathrm{(}\mathit{g}\mathrm{\sim }\mathit{N}\mathrm{(}\mathrm{0}\mathrm{,}\mathit{I}{\mathrm{\sigma }}_e^{\mathrm{2}}\mathrm{)}\mathrm{)}$. In this study, we only kept 2160 markers among the 3123 SNPs available in the genetic map. These 2160 markers correspond to the markers that were heterozygous for one of the two parents, only. As a consequence, the matrix of markers includes one kind of heterozygous (A/B) and one kind of homozygous markers (A/A), only. In the matrix of markers, a locus was then coded -1 when the two alleles were different (A/B), and was coded 1 when the two alleles were similar (A/A), whatever the heterozygous parent. Marker effect estimations were performed on phenotypic values collected in Experiment 1 data using the mixed.solve procedure of the rrBLUP package of R software (Endelman, 2011).

We estimated the genetic values of each parameter (G, (116×1)) for all genotypes in the population using the estimated marker effects (ĝ):

$\mathit{G}\mathit{=}\mathrm{\mu }\mathit{+}\mathit{W}\hat{\mathit{g}}\mathit{}\mathrm{\left(}\mathrm{8}\mathrm{\right)}$

with W the matrix of markers for each genotype (116 × 2160). In order to predict the phenotypic values of MAppleT parameters, markers effects were multiplied by the ratio between the standard deviation of observed phenotypes and the standard deviation of the genotypic predictions.

${\mathit{g}}_{\mathrm{2}}\mathit{=}\frac{\mathit{s}\mathit{d}\mathit{\left(}\mathit{Y}\mathit{\right)}}{\mathit{s}\mathit{d}\mathit{\left(}\mathit{G}\mathit{\right)}}\mathit{\times }\hat{\mathit{g}}\mathrm{\left(}\mathrm{9}\mathrm{\right)}$

The phenotypic values of MAppleT parameters (P, (116 × 1)) was calculed for each parameters and for all the genotypes as follows:

$\mathit{P}\mathit{=}\mathrm{\mu }\mathit{+}{\mathit{W}}_{\mathit{g}\mathrm{2}}\mathit{}\mathrm{\left(}\mathrm{10}\mathrm{\right)}$

The accuracy of the genome wide prediction model was assessed by testing the correlations between estimated and observed values of the MAppleT parameters, in three different ways. First, the accuracy of the prediction model was determined using all genotypes to estimate parameter values. Second, and following previous studies (Kumar et al., 2012; Fodor et al., 2014), the accuracy of the prediction was evaluated using a 10-fold cross validation. For this, genotypes were randomly assigned to one of the 10 equal folds. Each fold (validation population, 10% of the population) was predicted using marker effect estimations using the nine other folds (training population). In this case, the accuracy was calculated as the mean value of the correlations between predicted and observed phenotypes obtained for the 10 folds. Lastly, we also tested the accuracy of the prediction with a “leave-one-out” cross validation. In this method, each phenotype was predicted using marker effects estimated on the whole population without this genotype. The accuracy was calculated as the correlation between predicted and observed phenotypes on the whole population.

Implementation of Markers Effects in MAppleT and Output Evaluation

The values of the four parameters (IN_length, Leaf_area, RLE_GDD, and a_syll) for all the genotypes were calculated using the genome wide prediction model based on the matrices of marker effects and genotypes. Simulations were then performed with MAppleT with the environmental conditions of both experiments.

For validating the approach, the values of the three integrated architectural traits (Nb_Leaves, Trunk_length, and Nb_syll) were compared with observed values. Since the sylleptic branching model is stochastic, different values were obtained for the different simulations with the same set of genotypic parameters. The observed number of sylleptic laterals per genotype was thus compared with the mean number of sylleptic obtained after running five simulations.

The validation was performed in two consecutive steps. First, simulation outputs were compared with data from Experiment 1, which was used to parameterize the model, in order to evaluate the model capacity to simulate the genotypic variability of whole tree development based on markers effects. Second, the comparison was performed on data from Experiment 2 which were not used to parameterize the model in order to evaluate its performance under different environmental conditions. Simulations were run from budburst until the end of the growing season. In both experiments and accordingly to what is observed in the experimental site, budburst date, and the end of the growing season were set to April, 15 and September, 30, respectively.

The correlation coefficient, the RMSE, the relative RMSE (nRMSE), and the bias (BIAS) were used to compare simulations (s_i) and observations (o_i):

$\mathit{R}\mathit{M}\mathit{S}\mathit{E}=\sqrt{\frac{\mathrm{1}}{\mathit{n}}\underset{\mathit{i}\mathrm{=}\mathrm{1}}{\overset{\mathit{n}}{\mathrm{\Sigma }}}{\mathrm{(}{\mathit{O}}_{\mathit{i}}\mathit{-}{\mathit{S}}_{\mathit{i}}\mathrm{)}}^{\mathrm{2}}\mathrm{}}\mathrm{\left(}\mathrm{11}\mathrm{\right)}$

$\mathit{n}\mathit{R}\mathit{M}\mathit{S}\mathit{E}\mathit{-}\mathit{R}\mathit{M}\mathit{S}\mathit{E}\mathit{/}\overline{\mathit{o}}\mathrm{\left(}\mathrm{12}\mathrm{\right)}$

$\mathit{B}\mathit{I}\mathit{A}\mathit{S}\mathit{=}\frac{\mathrm{1}}{\mathit{n}}\underset{\mathit{i}\mathit{=}\mathrm{1}}{\overset{\mathit{n}}{\mathrm{\Sigma }}}\mathrm{(}{\mathit{S}}_{\mathit{i}}\mathit{-}{\mathit{O}}_{\mathit{i}}\mathrm{)}\mathrm{\left(}\mathrm{13}\mathrm{\right)}$

Results

Climatic Data and Phenotypic Traits

The analysis of temperature effect on the RLE showed that the mixed linear model 4 which includes the effect of TT computed with the single sine method, TT (see Supplementary Table 2) had the lowest BIC. Although BIC values between the different models were close, this sustains the hypothesis of a significant impact of temperature variations on RLE. Moreover, model 4 includes a genetic effect (β_ι) on the slope between RLE and TT (RLE_GDD) which also suggests that the slope values were genetically dependent.

TABLE 2

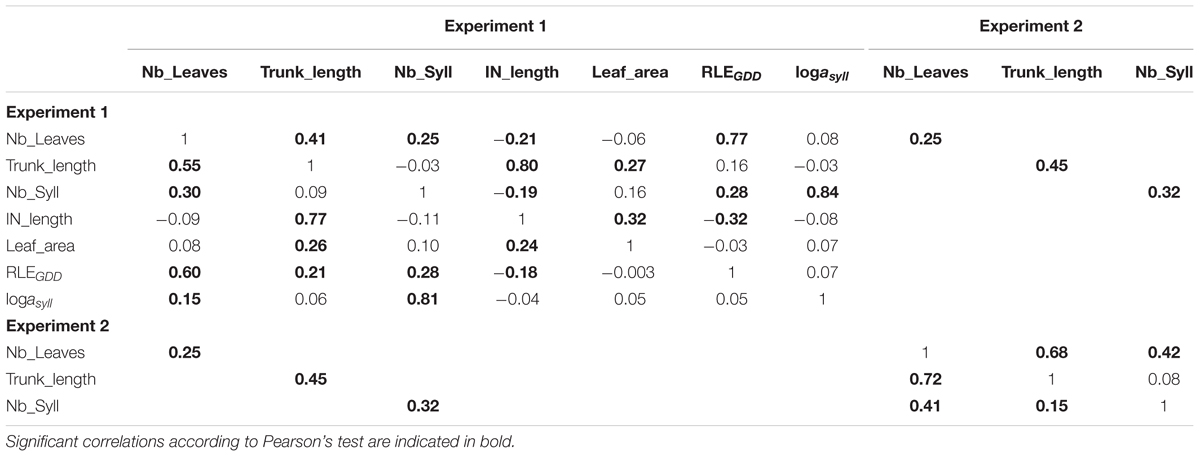
TABLE 2. Correlation between phenotypic (lower diagonal) and genetic values (upper diagonal) of either measured traits (Nb_Leaves, Trunk_length, Nb_Syll, IN_length, and Leaf_area) or estimated parameters (RLE_GDD, loga_syll) on 116 1-year-old hybrid apple trees in the two experiments (Experiments 1 and 2).

The cumulate daily thermal time (TT) during the growing season (15 April–31 September) was almost similar between the two experiments, even though slightly higher in Experiment 1 than in Experiment 2 (2278 and 2234 GDD, respectively). However, the annual dynamics were different. Indeed, daily thermal time was strongly higher during the first 30 days and was slightly lower during summer (June, August, and September) in Experiment 1 compared to Experiment 2 (Figure 1). For the two experiments, the highest GDD was observed at the end of July.

As the leaf emergence rate (RLE_d) and the probability of sylleptic lateral emergence directly depends on TT in our model, the evolution of these two variables followed the daily thermal time. The mean value of the leaf emergence rate expressed in growing degree-day (RLE_GDD) and estimated on data from Experiment 1 was 0.033 Leaf.GDD^-1 which corresponds to a duration between the emergence of two leaves of 30 GDD (∼3 days during the first growing month and 2 days during summer). The mean value of the estimated parameter loga_syll was -1.25. The mean value of loga_syll corresponded to a probability of emergence of a sylleptic lateral on each metamer of 0.095 during first growing months and of 0.143 during summer.

Compared to Experiment 1, phenotypic values observed in Experiment 2 were on average 5% higher for the number of leaves (Nb_Leaves), 12% lower for the trunk length (Trunk_length), and 48% higher for the number of sylleptic laterals (Nb_syll) and these differences were significant (Table 1). It must be noticed that the higher number of leaves in Experiment 2 compared to Experiment 1 is contradictory with the corresponding value of cumulated daily thermal time which was lower in Experiment 2.

The architectural traits (Nb_Leaves, Trunk_length, and Nb_syll) and MAppleT parameters (IN_length, Leaf_area, RLE_GDD, and loga_syll) showed intermediate (0.38) to high (0.86) heritabilities in both experiments (Table 1). The highest heritability values were found for IN_length in Experiment 1. Heritabilities for Trunk_length were similar whether computed considering the two experiments together or for each year separately. Conversely, heritability values were reduced by 26 and 32% for Nb_Leaves and Nb_syll, when considering either both years together or each year separately.

The analyses of correlations gave similar results if genetic or phenotypic correlations were considered (Table 2). Correlations between MAppleT parameters were low. Only the correlations between RLE_GDD and the mean internode length and between the leaf area and the mean internode length were significant (P = 0.004 and 0.0003, respectively). As expected, Nb_leaves, Trunk_length, and Nb_syll were strongly correlated to RLE_GDD, IN_length, and loga_syll, respectively. The correlations between the two experiments for the architectural traits Nb_Leaves, Trunk_length, and Nb_syll were significant but the correlation coefficients remained low (from 0.25 to 0.45).

Genomic Prediction and Its Accuracy

QTL detections on BLUPs of IN_length, Leaf_area, RLE_GDD, and loga_syll revealed only one QTL for IN_length which was the most heritable parameters (data not shown). This QTL was located on LG 12 and explained 16.9% of the genetic variability. It was associated with the SNP FB_0152374_L12_PA with a LOD score of 4.67. For the three other variables (RLE_GDD, loga_syll, and Leaf_area), no significant QTL could be detected. Because these variables were under genetic control (moderate to high heritability), the absence of detected QTL led us to assume that they were under the control of a high number of markers with low effect. We therefore tested a genome wide prediction model.

Correlations between mean observed phenotypes and predicted phenotypes with the genome wide estimation model and using all genotypes to estimate marker effects was 0.82 for RLE_GDD, 0.98 for IN_length, 0.87 for loga_syll, and 0.80 for Leaf_area, respectively (Figure 2). All these correlations were significant according to Pearson’s test (P < 0.05) showing the ability of the genome wide model to estimate parameter values from SNP markers. However, the prediction accuracies were notably lower using the cross validation methods (Figure 2). The mean accuracy from the 10-fold cross validation was 0.26 for RLE_GDD, 0.30 for IN_length, 0.15 for loga_syll, and 0.31 for Leaf_area, respectively. The standard deviation of the accuracy from the 10-fold cross validation was very high for the four variables: 0.23 for RLE_GDD, 0.30 for IN_length, 0.35 for loga_syll, and 0.24 for Leaf_area. The accuracy obtained using the “leave-one-out” cross validation were 0.20 for RLE_GDD, 0.30 for IN_length, 0.25 for loga_syll, and 0.30 for Leaf_area.

FIGURE 2

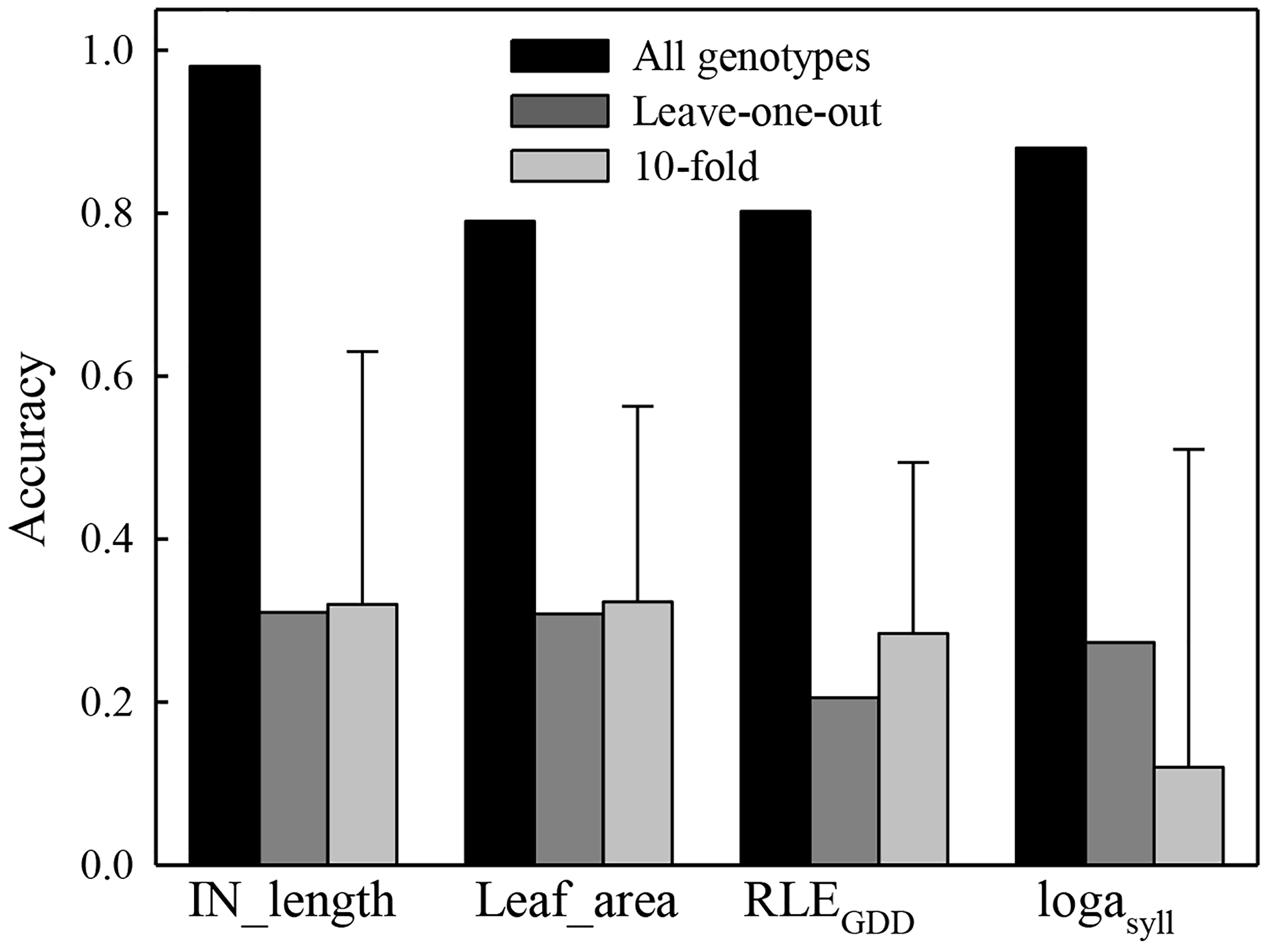
FIGURE 2. Accuracy of the genome wide predictions obtained using 116 1-year-old hybrid apple trees of a segregating population as training set, with a Leave-one-out cross validation and a 10-fold cross validation for four parameters (IN_length, Leaf_area, RLE_GDD, and loga_syll) of the MAppleT model. The error bar for the 10-fold cross validation was computed from the 10 values of correlations between the observed and predicted value of the validation population. For each fold, 90% of the population was randomly chosen as the training population and the other 10% were used as the validation population. For the leave-one-out cross validation, each phenotype was predicted using marker effects estimated on the whole population excluding this genotype. The accuracy was calculated once as the correlation between predicted and observed phenotypes for the whole population.

Simulation of 1 Year-Old Genotypes under Two Environmental Conditions

Simulations with MAppleT were performed under environmental conditions of Experiments 1 and 2. Under the environmental conditions of Experiment 1 (experiment used to parameterize MAppleT), correlations between observed and simulated values were equal to 0.65 for Nb_Leaves, 0.83 for Trunk_Length, and 0.80 for Nb_syll (Figure 3). These correlations were significant according to Pearson’s test (P < 0.05). The normalized RMSE (nRMSE) was low for the Nb_leaves (8%) and Trunk_length (10%) but high for Nb_syll (63%). The Nb_syll was correctly predicted for the genotypes with low number of sylleptic laterals but the difference between observation and simulation increased for genotypes with more than 10 sylleptic laterals. On average, the number of sylleptic was slightly overestimated (by 0.86). Conversely, Nb_leaves and Trunk_length were on average underestimated by 2.29 and 8.42 mm, respectively. The distribution of sylleptic laterals along the trunk was more homogeneous in the simulated population than in the observed one (Figure 4). Indeed, a large variation in this frequency that was not simulated by the model was observed along trunk between 10 and 30 nodes. However, the highest frequency of sylleptic laterals was obtained within the same internode rank zone (∼ at rank 25) and the decrease after node rank 40 was correctly simulated.

FIGURE 3

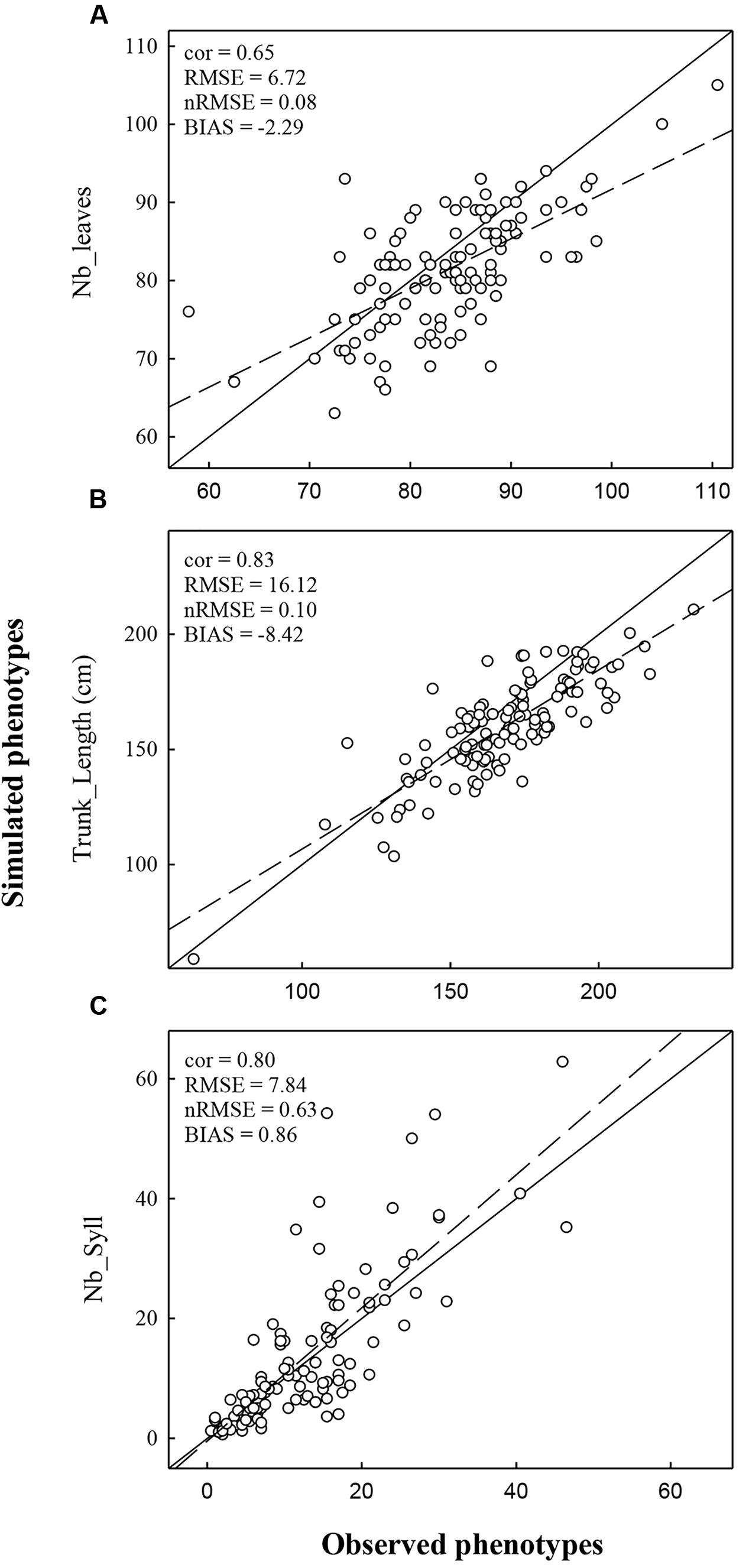
FIGURE 3. Comparison of observed and simulated phenotypes for the variable Nb_Leaves (A), Trunk_length (B), and Nb_Syll (C). Simulations were performed using climatic conditions of Experiment 1. The dashed line represents the regression line and the full line represents the 1:1 line.

FIGURE 4

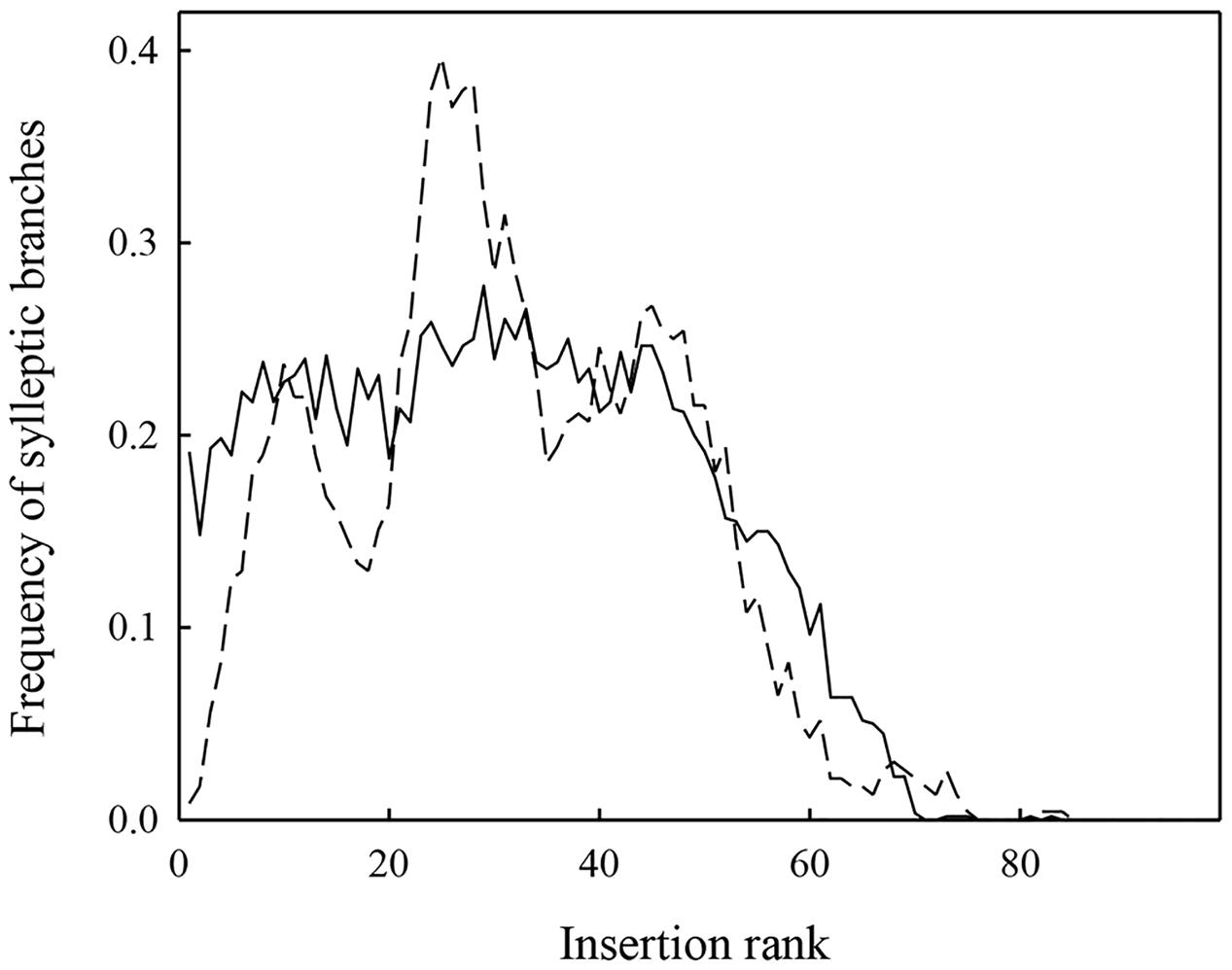
FIGURE 4. Distribution of the mean frequency of sylleptic laterals along the trunks for 116 1-year-old apple trees either simulated (full line) or observed (dashed line) in Experiment 1.

The performance of the model was also evaluated by comparing observed and predicted values obtained from simulations under the environmental condition of Experiment 2 which was not used to estimate marker effects. In Experiment 2, correlations between observed and simulated values were lower than in Experiment 1 (Figure 5). Correlations were low but significant for Trunk_length (0.30) and Nb_syll (0.29). The correlation was not significant for Nb_Leaves (0.10). The nRMSE obtained for Nb_leaves, Trunk_length, and Nb_syll were 20, 21, and 83%, respectively.

FIGURE 5

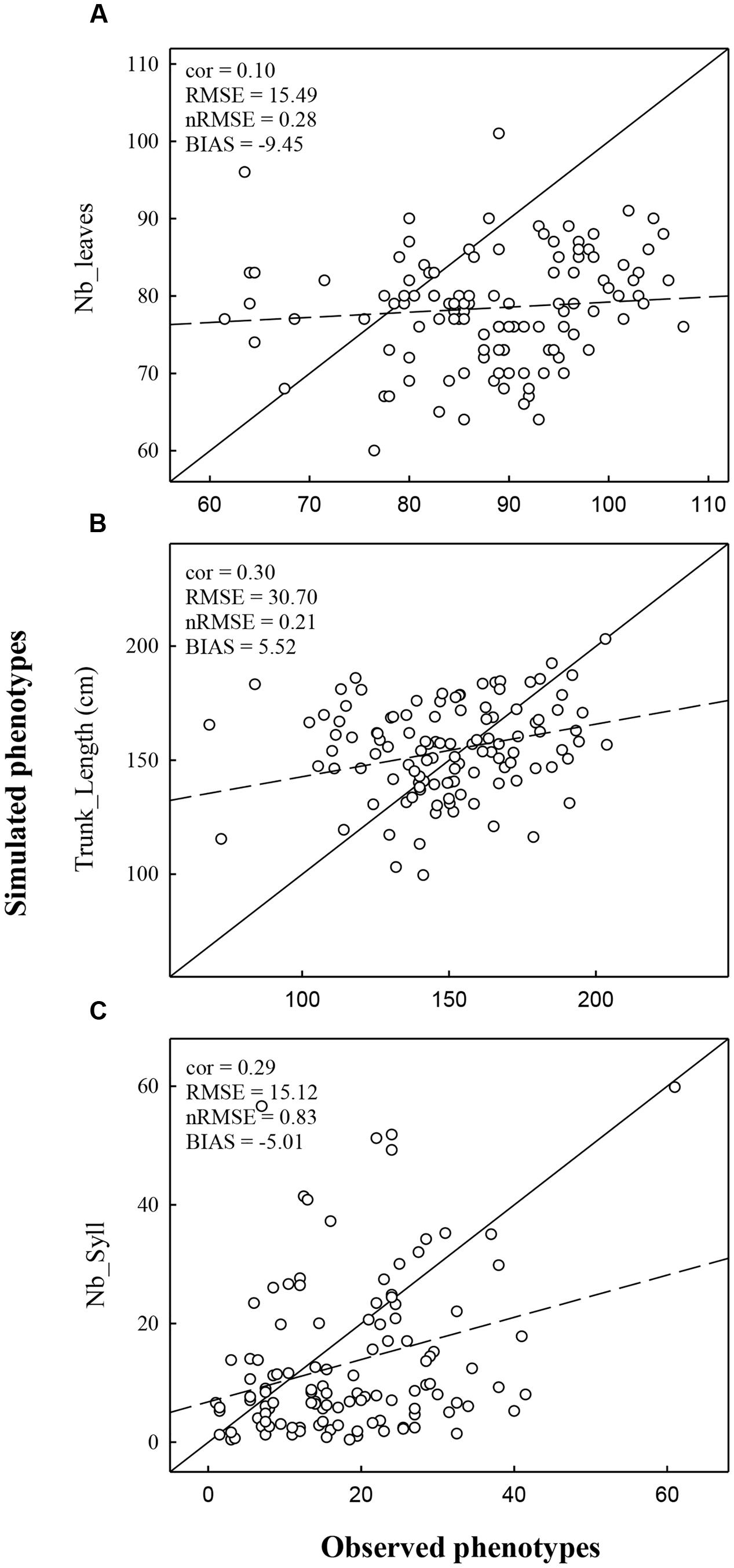
FIGURE 5. Comparison of observed and simulated phenotype for the variable Nb_Leaves (A), Trunk_length (B), and Nb_Syll (C). Simulations were realized using climatic conditions of Experiment 2. The dashed line represents the regression line and the full line represents the 1:1 line.

The total number of leaves was more strongly underestimated in Experiment 2 than Experiment 1 (bias was -9.45 and -2.29, respectively). This discrepancy resulted from the average number of leaves observed in Experiments 1 and 2 (83.57 and 87.86, respectively) which were not in accordance with the lower cumulate thermal time observed in Experiment 2 than in Experiment 1. Despite of the strong underestimation of the number of internodes (corresponding to the number of leaves), the trunk length was overestimated in Experiment 2, unlike Experiment 1. This probably results from an overestimation of the mean individual internode length in Experiment 2. Indeed, mean internode length in MAppleT was identical in the two simulations whereas their observed values were higher in Experiment 1 than in Experiment 2 (2.02 and 1.69 cm, respectively). The number of sylleptic laterals was highly underestimated in Experiment 2 (bias was -5.01). This is probably due to the underestimation of the leaf emergence rate which in turn affects the probability of sylleptic emergence (Equation 1).

The 1-year-old apple trees simulated in the environmental condition of Experiment 1 exhibited a large range of phenotypes. Genotypes with high number of leaves and high trunk length or with low number of leaves and high trunk length were simulated (Figure 6). This suggests low correlations between the simulated traits. Indeed, the simulated architectural traits were slightly correlated (Table 3) with correlation coefficients similar to those observed (Table 2). The correlations between the architectural traits obtained from simulations in the two climatic conditions were close to 1 (Table 3) probably showing that the model did not generate large GxE interaction.

FIGURE 6

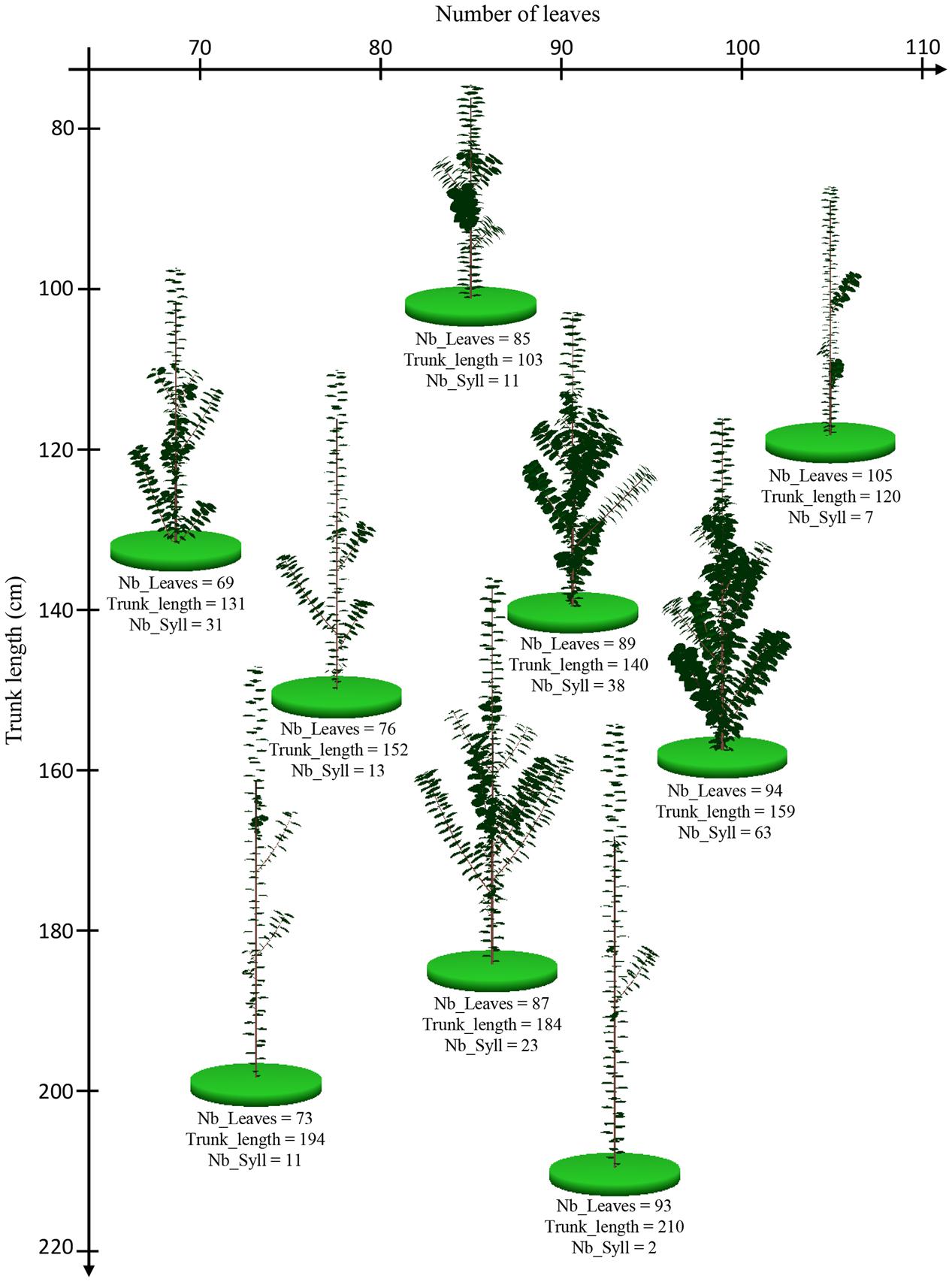
FIGURE 6. Graphical outputs of MAppleT simulations for nine apple tree genotypes with contrasting architectures. The position of trunk base of the virtual trees on each axis of the graphic indicates their number of leaves on the trunk (Nb_Leaves, X-axis) and the trunk length (Trunk_length, Y-axis), respectively. The values of the number of leaves, trunk length, and number of sylleptic laterals (Nb_Syll) are indicated under each virtual tree.

TABLE 3

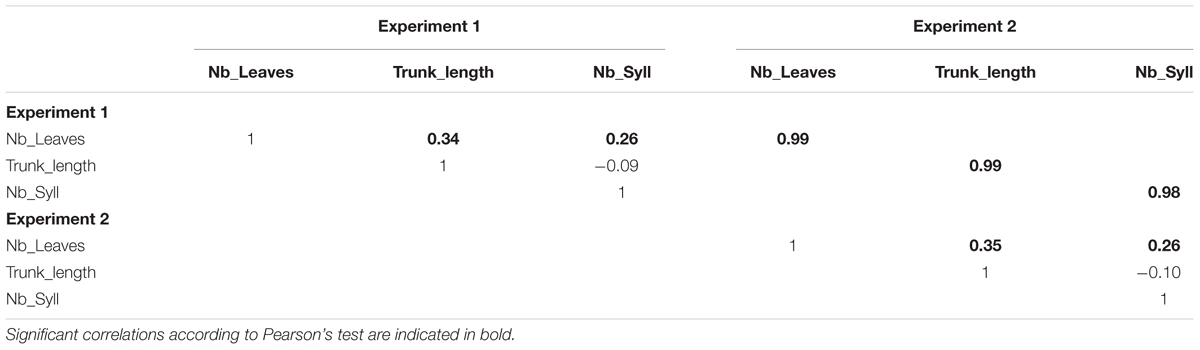
TABLE 3. Correlations between architectural traits simulated with MAppleT and genotypic marker effects for 116 1-year-old hybrid apple genotypes in two experimental climatic conditions.

Discussion

This paper presents a proposition for linking a FSPM, MAppleT, with genetic information on growth and branching model parameters, estimated on an apple tree segregating population. Mean heritability values of architectural traits (trunk length, number of leaves, and number of sylleptic laterals) were estimated with two independent datasets which provided similar results. However, heritability values were lower than those obtained by Segura et al. (2006), on a subsample of 50 hybrids of the same progeny, observed at the same age (1-year-old) but planted in a different year (2003) and with three replicates per genotype (Segura et al., 2006). Even though heritability values were similar in Experiments 1 and 2, both phenotypic and genetic correlations between these experiments were low. This suggests that the proportion of phenotypic variation explained by the genotype is constant but also that the genetic values vary between years. This could result from differences in the climatic conditions in the plantation years, from the variability in the plant material obtained after grafting and from the existence of large GxE interactions. This GxE interaction has been previously observed in clonally propagated plants (Alspach and Oraguzie, 2002; Chagné et al., 2014). Nevertheless, having re-multiplied the same progeny several times is quite unique for a perennial crop in which a single orchard and a low number of replicates per genotype are often considered. Our results suggest that part of the GxE interaction could result from propagation effect and confirm that more attention should be paid in the future to the phenotypes repeatability, through multi-sites or multi-years experiments, in order to improve our understanding of the potential sources of variability (Myles et al., 2009).

Previous studies aiming at linking FSPM with genetic information have been based on QTL effects only (Xu et al., 2011). Here, the marker effects were estimated first with interval mapping methods but a few QTLs could be detected. This contrasts with previous studies (Segura et al., 2007, 2009) and could result from a lack of precision of either genotypes or phenotypes and from the large GxE interaction.

To overcome this, our strategy was to perform a genome wide estimation of marker effects for the four studied parameters. Correlations between estimated and observed values from the genome wide prediction model were high, showing that the model was able to estimate genotypic differences from SNP polymorphisms. However, during the cross validation, the accuracy was much lower even though similar to previous studies on apple (Kumar et al., 2012; Muranty et al., 2015) or on other species (Rutkoski et al., 2013; Fodor et al., 2014). This highlights the limit of our genome wide prediction model to predict phenotypic values for genotypes that are not included in the training set. The prediction model accuracy is influenced by the density of the genetic map (Kumar et al., 2012; Heslot et al., 2013), the population size (Brito et al., 2011), and the heritability of traits (Combs and Bernardo, 2013; Muranty et al., 2015). Among the arguments mentioned above, the population size is probably the most limiting factor in the present study. In that context, high throughout methods such as airborne imagery (Virlet et al., 2014) or 3D laser scanning (Boudon et al., 2014) could be useful to provide phenotypic data related to plant functioning or architecture on large sets of genotypes. Other statistical models used to predict markers effects could also be tested. Bayesian models that include a selection of variables together with a shrinkage parameter for marker effects could be tested in order to reduce the risk of over-fitting. Indeed, this over-fitting problem could explain the low ability of our modeling approach to predict genotypes that were not included in the training set (de los Campos et al., 2013). Nevertheless, even if these methods could be relevant, several studies have compared the predictions for the different statistical methods and have shown similar accuracy whatever the method used (e.g., Resende et al., 2012; Fodor et al., 2014).

The predicted values of four MAppleT parameters (IN_length, Leaf_area, RLE_GDD, and loga_syll) were used to simulate tree development with MAppleT and three integrative traits (Nb_Leaves, Trunk_length, and Nb_syll) were considered for validating our approach. The RMSE was low for the three variables when the genotypes were simulated in climatic conditions of Experiment 1, used to parameterize the genome wide model. This demonstrates the feasibility and relevance of the approach, i.e., including genetic information into a FSPM. As expected, the number of sylleptic laterals was correctly simulated for Experiment 1, consistently with the fact that this variable was used to estimate the probability of sylleptic lateral emergence. Moreover, the node ranks along the trunks at which the frequency of sylleptic laterals was the highest was similar to observations. The decrease in sylleptic frequency after node rank 40 was also consistent with observations. This supports the assumption we made of a close relationship between the RLE and the sylleptic branching probability. However, the sylleptic laterals were more homogeneously distributed along the trunks in the simulated population than in observations. This suggests that the link between the RLE and the sylleptic branching could be stronger or more complex than modeled in this study. Further refinements in the link between the dynamics of primary growth and immediate branching, considering non-linear relationships between RLE and branching probability (Génard et al., 1994), could be considered.

Consistently with the discrepancy between the number of leaves and the GDD in the two observation years, the comparison of the integrated variables simulated and observed with the climatic conditions of Experiment 2 generated high RMSE. As previously stated for peach tree by Davidson et al. (2015), our results confirm that modeling the leaf emergence rate based on GDD is not sufficient, in particular for trees grown in field conditions. Other environmental factors are likely to affect the RLE in open field conditions, such as the soil resource availability. Since the emergence of sylleptic laterals depended in our model on the leaf emergence rate only, discrepancy was also obtained for this variable when simulated with Experiment 2 conditions.

Despite these limitations and the necessity of further improvements of the predictions based on genome wide information, the MAppleT model including the genotypic marker effects simulate genotypes with contrasting architectures for which correlations among simulated architectural traits were similar to observations. This suggests that the different hybrid genomes corresponding to different trait recombination were correctly taken into account. The existence of numerous recombination of architectural traits in F1 hybrids and the difficulties that this generates for the qualitative assessment of hybrid architecture was previously underlined by Segura et al. (2009). The presented approach thus opens a new way to experiment the consequences of genome recombination on integrated phenotypes. However, further evaluation on the agronomic performance of each genotype when the tree will be mature would be useful to complement the present study. Even though quantitative genetic models allows studying the genetic determinism of several traits jointly though multi-traits approaches (e.g., Mathews et al., 2008; Alimi et al., 2013), the exploration of several, possibly not correlated, traits remains a challenge to facilitate the exploration of plant ideotypes (Martre et al., 2015). Indeed, ideotypes are by definition composed of several desirable traits. FSPMs, by providing simulations of plant architecture and allowing the investigation of the impact of architectural traits on integrative traits such as light interception or biomass production (e.g., Da Silva et al., 2014) constitute a powerful tool to assess phenotype performance.

The integration of other environmental factors in the present modeling approach would be necessary to extent the domain of validity and to further analyze GxE interactions. This could be achieved by integrating other environmental response curves and adding the effects of each individual environmental factor on plant growth processes as done for instance by Reymond et al. (2003), Hammer et al. (2006), or Casadebaig et al. (2011). Alternative approaches including an intermediate plant variable that takes into account the combined effects of many environmental factors could be relevant. In this way, functional structural plant models considering the impact of C source-sink balances on plant and organ growth through a variable (the index of competition for carbon) reflecting the internal trophic state of the plant have been proposed (e.g., Luquet et al., 2006; Mathieu et al., 2009; Pallas et al., 2013). Such approaches could be appropriate to reduce the risk of overestimating the environmental effects that result from the additive models used in above mentioned studies (Reymond et al., 2003; Hammer et al., 2006; Casadebaig et al., 2011). In this present study, the RLE could be considered as an intermediate variable since it determines the branching probability. Presently, RLE was affected by temperature, only but its use as an intermediate variable could be tested under other environmental constraints such as water stress.

Finally, the extension of such models coupling FSPM and genetic information to larger germplasms and to the generation of a new simulated mapping population, as recently proposed in rice (Xu and Buck-Sorlin, 2016), will likely be a new research avenue in interface with eco-physiology, process-based, and gene-based modeling (Technow et al., 2015). For perennials, the extension to multi-years development of trees will represent another complexity that could be tackled based on knowledge on genetic determinisms over years (Segura et al., 2008, 2009).

Author Contributions

EC and BP contributed to design the work. VM and BP performed the modeling tasks and analyzed the data. VM, BP, and EC wrote the manuscript. EC contributed to data acquisition.

Funding

The post doctoral fellowship of VM was funded by ANR (Agence Nationale de la recherche) in the framework of the French-German ANR-DFG FSPMapple project under the reference number ANR-14-CE35-0017.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge J.M. Legave, V. Segura, and S. Martinez for their contribution to field measurements. We are grateful to Y. Guédon for their helpful discussion regarding sylleptic branching modeling.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fpls.2016.02065/full#supplementary-material

References

Alimi, N. A., Bink, M. C. A. M., Dieleman, J. A., Magán, J. J., Wubs, A. M., Palloix, A., et al. (2013). Multi-trait and multi-environment QTL analyses of yield and a set of physiological traits in pepper. Theor. Appl. Genet. 126, 2597–2625. doi: 10.1007/s00122-013-2160-2163

PubMed Abstract | CrossRef Full Text | Google Scholar

Allard, A., Bink, M. C. A. M., Martinez, S., Kelner, J.-J., Legave, J.-M., Di Guardo, M., et al. (2016). Detecting QTLs and putative candidate genes involved in budbreak and flowering time in an apple multiparental population. J. Exp. Bot. 67, 2875–2888. doi: 10.1093/jxb/erw130

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, M. T., Prusinkiewicz, P., and DeJong, T. M. (2005). Using L-systems for modeling source–sink interactions, architecture and physiology of growing trees: the L-PEACH model. New Phytol. 166, 869–880. doi: 10.1111/j.1469-8137.2005.01348.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Alméras, T., Gril, J., and Costes, E. (2002). Bending of apricot tree branches under the weight of axillary growth: test of a mechanical model with experimental data. Trees 16, 5–15. doi: 10.1007/s00468-001-0139-131

CrossRef Full Text | Google Scholar

Alspach, P. A., and Oraguzie, N. C. (2002). Estimation of genetic parameters of apple (Malus domestica) fruit quality from open-pollinated families. N. Z. J. Crop Hortic. Sci. 30, 219–228. doi: 10.1080/01140671.2002.9514218

CrossRef Full Text | Google Scholar

Antanaviciute, L., Fernández-Fernández, F., Jansen, J., Banchi, E., Evans, K. M., Viola, R., et al. (2012). Development of a dense SNP-based linkage map of an apple rootstock progeny using the Malus infinium whole genome genotyping array. BMC Genomics 13:203. doi: 10.1186/1471-2164-13-203

PubMed Abstract | CrossRef Full Text | Google Scholar

Beveridge, C. A. (2006). Axillary bud outgrowth: sending a message. Curr. Opin. Plant Biol. 9, 35–40. doi: 10.1016/j.pbi.2005.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Bianco, L., Cestaro, A., Sargent, D. J., Banchi, E., Derdak, S., Guardo, M. D., et al. (2014). Development and validation of a 20K single nucleotide polymorphism (SNP) whole genome genotyping array for apple (Malus × domestica Borkh). PLoS ONE 9:e110377. doi: 10.1371/journal.pone.0110377

PubMed Abstract | CrossRef Full Text | Google Scholar

Boudon, F., Preuksakarn, C., Ferraro, P., Diener, J., Nacry, P., Nikinmaa, E., et al. (2014). Quantitative assessment of automatic reconstruction of branching systems obtained from laser scanning. Ann. Bot. 114, 853–862. doi: 10.1093/aob/mcu062

PubMed Abstract | CrossRef Full Text | Google Scholar

Brito, F. V., Neto, J. B., Sargolzaei, M., Cobuci, J. A., and Schenkel, F. S. (2011). Accuracy of genomic selection in simulated populations mimicking the extent of linkage disequilibrium in beef cattle. BMC Genet. 12:80. doi: 10.1186/1471-2156-12-80

PubMed Abstract | CrossRef Full Text | Google Scholar

Casadebaig, P., Guilioni, L., Lecoeur, J., Christophe, A., Champolivier, L., and Debaeke, P. (2011). SUNFLO, a model to simulate genotype-specific performance of the sunflower crop in contrasting environments. Agric. For. Meteorol. 151, 163–178. doi: 10.1016/j.agrformet.2010.09.012

CrossRef Full Text | Google Scholar

Chagné, D., Crowhurst, R. N., Troggio, M., Davey, M. W., Gilmore, B., Lawley, C., et al. (2012). Genome-wide SNP detection, validation, and development of an 8K SNP array for apple. PLoS ONE 7:e31745. doi: 10.1371/journal.pone.0031745

PubMed Abstract | CrossRef Full Text | Google Scholar

Chagné, D., Dayatilake, D., Diack, R., Oliver, M., Ireland, H., Watson, A., et al. (2014). Genetic and environmental control of fruit maturation, dry matter and firmness in apple (Malus × domestica Borkh.). Hortic. Res. 1:14046. doi: 10.1038/hortres.2014.46

PubMed Abstract | CrossRef Full Text | Google Scholar

Cline, M. G. (2000). Execution of the auxin replacement apical dominance experiment in temperate woody species. Am. J. Bot. 87, 182–190. doi: 10.2307/2656904

PubMed Abstract | CrossRef Full Text | Google Scholar

Combs, E., and Bernardo, R. (2013). Accuracy of genomewide selection for different traits with constant population size, heritability, and number of markers. Plant Genome 6, 1–7. doi: 10.3835/plantgenome2012.11.0030

CrossRef Full Text | Google Scholar

Costes, E., Smith, C., Renton, M., Guédon, Y., Prusinkiewicz, P., and Godin, C. (2008). MAppleT: simulation of apple tree development using mixed stochastic and biomechanical models. Funct. Plant Biol. 35, 936–950. doi: 10.1071/FP08081

CrossRef Full Text | Google Scholar

Da Silva, D., Han, L., Faivre, R., and Costes, E. (2014). Influence of the variation of geometrical and topological traits on light interception efficiency of apple trees: sensitivity analysis and metamodelling for ideotype definition. Ann. Bot. 114, 739–752. doi: 10.1093/aob/mcu034

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidson, A., Da Silva, D., Quintana, B., and DeJong, T. M. (2015). The phyllochron of Prunus persica shoots is relatively constant under controlled growth conditions but seasonally increases in the field in ways unrelated to patterns of temperature or radiation. Sci. Hortic. 184, 106–113. doi: 10.1016/j.scienta.2014.12.033

CrossRef Full Text | Google Scholar

Davidson, R., and Mackinnon, J. G. (2004). Econometric Theory and Methods. New York, NY: Oxford University Press.

Google Scholar

de los Campos, G., Hickey, J. M., Pong-Wong, R., Daetwyler, H. D., and Calus, M. P. L. (2013). Genome regression and prediction methods applied to plant and animal breeding. Genetics 193, 327–345. doi: 10.1534/genetics.112.143313

PubMed Abstract | CrossRef Full Text | Google Scholar

De Wit, I., Keulemans, J., and Cook, N. C. (2002). Architectural analysis of 1-year-old apple seedlings according to main shoot growth and sylleptic branching characteristics. Trees 16, 473–478. doi: 10.1007/s00468-002-0189-z

CrossRef Full Text | Google Scholar

DeJong, T. M., Da Silva, D., Vos, J., and Escobar-Gutiérrez, A. J. (2011). Using functional–structural plant models to study, understand and integrate plant development and ecophysiology. Ann. Bot. 108, 987–989. doi: 10.1093/aob/mcr257

CrossRef Full Text | Google Scholar

Di Guardo, M., Micheletti, D., Bianco, L., Putten, H. J. J. K., Longhi, S., Costa, F., et al. (2015). ASSIsT: an automatic SNP scoring tool for in- and outbreeding species. Bioinformatics 31, 3873–3874. doi: 10.1093/bioinformatics/btv446

PubMed Abstract | CrossRef Full Text | Google Scholar

Donald, C. M. (1968). The breeding of crop ideotypes. Euphytica 17, 385–403. doi: 10.1007/BF00056241

CrossRef Full Text | Google Scholar

Endelman, J. B. (2011). Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 4, 250–255. doi: 10.3835/plantgenome2011.08.0024

CrossRef Full Text | Google Scholar

Evers, J. B., Vos, J., Fournier, C., Andrieu, B., Chelle, M., and Struik, P. C. (2007). An architectural model of spring wheat: evaluation of the effects of population density and shading on model parameterization and performance. Ecol. Model. 200, 308–320. doi: 10.1016/j.ecolmodel.2006.07.042

CrossRef Full Text | Google Scholar

Fodor, A., Segura, V., Denis, M., Neuenschwander, S., Fournier-Level, A., Chatelet, P., et al. (2014). Genome-wide prediction methods in highly diverse and heterozygous species: proof-of-concept through simulation in grapevine. PLoS ONE 9:e110436. doi: 10.1371/journal.pone.0110436

PubMed Abstract | CrossRef Full Text | Google Scholar

Fournier, C., Andrieu, B., Ljutovac, S., and Saint-Jean, S. (2003). “ADEL-wheat: a 3D architectural model of wheat development,” in Proceedings of the 2003 International Symposium on Plant Growth Modeling, Simulation, Visualization and Their Applications, eds B.-G. Hu and M. Jaeger (Beijing: Tsinghua University Press), 54–63.

Google Scholar

Génard, M., Pagès, L., and Kervella, J. (1994). Relationship between sylleptic branching and components of parent shoot development in the peach tree. Ann. Bot. 74, 465–470. doi: 10.1006/anbo.1994.1142

CrossRef Full Text | Google Scholar

Godin, C., and Caraglio, Y. (1998). A multiscale model of plant topological structures. J. Theor. Biol. 191, 1–46. doi: 10.1006/jtbi.1997.0561

PubMed Abstract | CrossRef Full Text | Google Scholar

Hallé, F., Oldeman, R. A. A., and Tomlinson, P. B. (1978). Tropical Trees and Forests. Berlin: Springer.

Google Scholar

Hammer, G. L., Cooper, M., Tardieu, F., Welch, S., Walsh, B., and Van Eeuwijk, F. (2006). Models for navigating biological complexity in breeding improved crop plants. Trends Plant Sci. 11, 587–593. doi: 10.1016/j.tplants.2006.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Heffner, E. L., Sorrells, M. E., and Jannink, J.-L. (2009). Genomic Selection for Crop Improvement. Crop Sci. 49, 1–12. doi: 10.2135/cropsci2008.08.0512

CrossRef Full Text | Google Scholar

Heslot, N., Rutkoski, J., Poland, J., Jannink, J.-L., and Sorrells, M. E. (2013). Impact of marker ascertainment bias on genomic selection accuracy and estimates of genetic diversity. PLoS ONE 8:e74612. doi: 10.1371/journal.pone.0074612

PubMed Abstract | CrossRef Full Text | Google Scholar

Jirasek, C., Prusinkiewicz, P., and Moulia, B. (2000). Integrating biomechanics into developmental plant models expressed using L-systems. Plant Biomech. 24, 615–624.

Google Scholar

Kervella, J., Pagès, L., and Génard, M. (1995). Genotypic differences in the leaf emergence rate of young peach trees. J. Am. Soc. Hortic. Sci. 120, 278–282.

Google Scholar

Knapp, S. J., Stroup, W. W., and Ross, W. M. (1985). Exact confidence intervals for heritability on a progeny mean basis. Crop Sci. 25, 192–194. doi: 10.2135/cropsci1985.0011183X002500010046x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, S., Chagné, D., Bink, M. C. A. M., Volz, R. K., Whitworth, C., and Carlisle, C. (2012). Genomic selection for fruit quality traits in apple (Malus × domestica Borkh.). PLoS ONE 7:e36674. doi: 10.1371/journal.pone.0036674

PubMed Abstract | CrossRef Full Text | Google Scholar

Lauri, P.-E., and Costes, E. (2009). Does knowledge on fruit tree architecture and its implications for orchard management improve horticultural sustainability? An overview of recent advances in the apple. Acta Hortic. 87, 243–249. doi: 10.13140/2.1.3307.6486

CrossRef Full Text | Google Scholar

Lescourret, F., Ben Mimoun, M., and Génard, M. (1998). A simulation model of growth at the shoot-bearing fruit level: I. Description and parameterization for peach. Eur. J. Agron. 9, 173–188. doi: 10.1016/S1161-0301(98)00035-5

CrossRef Full Text | Google Scholar

Lespinasse, Y. (1992). “Le pommier,” in Amélioration des Espèces Végétales Cultivées—Objectifs et Critères de Sélection, eds A. Gallais and H. Bannerot (Paris: INRA), 579–594.

Google Scholar

Letort, V., Mahe, P., Cournède, P.-H., de Reffye, P., and Courtois, B. (2008). Quantitative genetics and functional–structural plant growth models: simulation of quantitative trait loci detection for model parameters and application to potential yield optimization. Ann. Bot. 101, 1243–1254. doi: 10.1093/aob/mcm197

PubMed Abstract | CrossRef Full Text | Google Scholar

Lopez, G., Pallas, B., Martinez, S., Lauri, P.-E., Regnard, J.-L., Durel, C. E., et al. (2015). Genetic variation of morphological traits and transpiration in an apple core collection under well watered conditions: toward the identification of morphotypes with high water use efficiency. PLoS ONE 10:e0145540. doi: 10.1371/journal.pone.0145540

PubMed Abstract | CrossRef Full Text | Google Scholar

Luquet, D., Dingkuhn, M., Kim, H., Tambour, L., and Clément-Vidal, A. (2006). Ecomeristem, a model of morphogenesis and competition among sinks in rice. 1. Concept, validation and sensitivity analysis. Funct. Plant Biol. 33, 309–323. doi: 10.1071/FP05266

CrossRef Full Text | Google Scholar

Martre, P., Quilot-Turion, B., Luquet, D., Memmah, M.-M. O.-S., Chenu, K., and Debaeke, P. (2015). “Model-assisted phenotyping and ideotype design,” in Crop Physiology: Applications for Genetic Improvement and Agronomy, ed. D. F. Calderini (San Diego, CA: Academic Press), 349–373.

Google Scholar

Mathews, K. L., Malosetti, M., Chapman, S., McIntyre, L., Reynolds, M., Shorter, R., et al. (2008). Multi-environment QTL mixed models for drought stress adaptation in wheat. Theor. Appl. Genet. 117, 1077–1091. doi: 10.1007/s00122-008-0846-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathieu, A., Cournède, P.-H., Letort, V., Barthélémy, D., and de Reffye, P. (2009). A dynamic model of plant growth with interaction between development and functional mechanisms to study plant structural plasticity related to trophic competition. Ann. Bot. 103, 1173–1186. doi: 10.1093/aob/mcp054

PubMed Abstract | CrossRef Full Text | Google Scholar

Meuwissen, T. H. E., Hayes, B. J., and Goddard, M. E. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.

PubMed Abstract | Google Scholar

Morgan, D. C., Warrington, I. J., and Halligan, E. A. (1985). Effect of temperature and photosynthetic photon flux density on vegetative growth of kiwifruit (Actinidia chinensis). N. Z. J. Agric. Res. 28, 109–116. doi: 10.1080/00288233.1985.10427003

CrossRef Full Text | Google Scholar

Muranty, H., Troggio, M., Sadok, I. B., Rifaï, M. A., Auwerkerken, A., Banchi, E., et al. (2015). Accuracy and responses of genomic selection on key traits in apple breeding. Hortic. Res. 2, 15060. doi: 10.1038/hortres.2015.60

PubMed Abstract | CrossRef Full Text | Google Scholar

Myles, S., Peiffer, J., Brown, P. J., Ersoz, E. S., Zhang, Z., Costich, D. E., et al. (2009). Association mapping: 623 critical considerations shift from genotyping to experimental design. Plant Cell 21, 2194–2202. doi: 10.1105/tpc.109.068437

PubMed Abstract | CrossRef Full Text

Niinemets, Ü. (2010). A review of light interception in plant stands from leaf to canopy in different plant functional types and in species with varying shade tolerance. Ecol. Res. 25, 693–714. doi: 10.1007/s11284-010-0712-4

PubMed Abstract | CrossRef Full Text

Pallas, B., Clément-Vidal, A., Rebolledo, M.-C., Soulié, J.-C., and Luquet, D. (2013). Using plant growth modeling to analyze C source-sink relations under drought: inter- and intraspectific comparison. Front. Plant Sci. 4:437. doi: 10.3389/fpls.2013.00437

PubMed Abstract | CrossRef Full Text

Pallas, B., Louarn, G., Christophe, A., Lebon, E., and Lecoeur, J. (2008). Influence of intra-shoot trophic competition on shoot development in two grapevine cultivars. Physiol. Plant. 134, 49–63. doi: 10.1111/j.1399-3054.2008.01100.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Perez, R. P. A., Pallas, B., Moguédec, G. L., Rey, H., Griffon, S., Caliman, J.-P., et al. (2016). Integrating mixed-effect models into an architectural plant model to simulate inter- and intra-progeny variability: a case study on oil palm (Elaeis guineensis Jacq.). J. Exp. Bot. 67, 4507–4521. doi: 10.1093/jxb/erw203

PubMed Abstract | CrossRef Full Text | Google Scholar

Perttunen, J., Sievänen, R., and Nikinmaa, E. (1998). LIGNUM: a model combining the structure and the functioning of trees. Ecol. Model. 108, 189–198. doi: 10.1016/S0304-3800(98)00028-3

CrossRef Full Text | Google Scholar

Peyhardi, J., Costes, E., Caraglio, Y., Lauri, P.-E., Trottier, C., and Guédon, Y. (2013). “Integrative models for analyzing jointly shoot growth and branching patterns,” in Proceedings of the 7th International Conference on Functional Structure Plant Models, (Saariselkä: Finnish Society of Forest Science), 371.

Google Scholar

Powell, G. R. (1991). Preformed and neoformed extension of shoots and sylleptic branching in relation to shoot length in Tsuga canadensis. Trees 5, 107–116. doi: 10.1007/BF00227493

CrossRef Full Text | Google Scholar

Reinhardt, D., and Kuhlemeier, C. (2002). Plant architecture. EMBO Rep. 3, 846–851. doi: 10.1093/embo-reports/kvf177

PubMed Abstract | CrossRef Full Text | Google Scholar

Remphrey, W. R., and Powell, G. R. (1985). Crown architecture of Larix laricina saplings: sylleptic branching on the main stem. Can. J. Bot. 63, 1296–1302. doi: 10.1139/b85-180

CrossRef Full Text | Google Scholar

Resende, M. F. R., Muñoz, P., Resende, M. D. V., Garrick, D. J., Fernando, R. L., Davis, J. M., et al. (2012). Accuracy of genomic selection methods in a standard data set of loblolly pine (Pinus taeda L.). Genetics 190, 1503–1510. doi: 10.1534/genetics.111.137026

PubMed Abstract | CrossRef Full Text | Google Scholar

Reymond, M., Muller, B., Leonardi, A., Charcosset, A., and Tardieu, F. (2003). Combining quantitative trait loci analysis and an ecophysiological model to analyze the genetic variability of the responses of maize leaf grwoth to temperature and water deficit. Plant Physiol. 131, 664–675. doi: 10.1104/pp.013839

PubMed Abstract | CrossRef Full Text | Google Scholar

Rötter, R. P., Tao, F., Höhn, J. G., and Palosuo, T. (2015). Use of crop simulation modelling to aid ideotype design of future cereal cultivars. J. Exp. Bot. 66, 3463–3476. doi: 10.1093/jxb/erv098

PubMed Abstract | CrossRef Full Text | Google Scholar

Rutkoski, J. E., Poland, J., Jannink, J.-L., and Sorrells, M. E. (2013). Imputation of unordered markers and the impact on genomic selection accuracy. G3 (Bethesda) 3, 427–439. doi: 10.1534/g3.112.005363

PubMed Abstract | CrossRef Full Text | Google Scholar

Segura, V., Cilas, C., and Costes, E. (2008). Dissecting apple tree architecture into genetic, ontogenetic and environmental effects: mixed linear modelling of repeated spatial and temporal measures. New Phytol. 178, 302–314. doi: 10.1111/j.1469-8137.2007.02374.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Segura, V., Cilas, C., Laurens, F., and Costes, E. (2006). Phenotyping progenies for complex architectural traits: a strategy for 1-year-old apple trees (Malus x domestica Borkh.). Tree Genet. Genomes 2, 140–151. doi: 10.1007/s11295-006-0037-1

CrossRef Full Text | Google Scholar

Segura, V., Denancé, C., Durel, C.-E., and Costes, E. (2007). Wide range QTL analysis for complex architectural traits in a 1-year-old apple progeny. Genome 50, 159–171. doi: 10.1139/G07-002

PubMed Abstract | CrossRef Full Text | Google Scholar

Segura, V., Kelner, J. J., Lauri, P. E., and Costes, E. (2009). Towards a strategy for phenotyping architectural traits in mature F1 hybrids of an apple progeny. Acta Hortic. 814, 169–176. doi: 10.17660/ActaHortic.2009.814.21

CrossRef Full Text | Google Scholar

Sussex, I. M., and Kerk, N. M. (2001). The evolution of plant architecture. Curr. Opin. Plant Biol. 4, 33–37. doi: 10.1016/S1369-5266(00)00132-1

CrossRef Full Text | Google Scholar

Technow, F., Messina, C. D., Totir, L. R., and Cooper, M. (2015). Integrating crop growth models with whole genome prediction through approximate bayesian computation. PLoS ONE 10:e0130855. doi: 10.1371/journal.pone.0130855

PubMed Abstract | CrossRef Full Text | Google Scholar

Valladares, F., Skillman, J. B., and Pearcy, R. W. (2002). Convergence in light capture efficiencies among tropical forest understory plants with contrasting crown architectures: a case of morphological compensation. Am. J. Bot. 89, 1275–1284. doi: 10.3732/ajb.89.8.1275

PubMed Abstract | CrossRef Full Text | Google Scholar

Van de Weg, W. E., Di Guardo, M., Koehorst-van Putten, H., Longhi, S., Noordijk, Y., Muranty, H., et al. (2013). A Pipeline for Robust Marker Calling from Infinium SNP Arrays for Diploid Crops. Available at: https://hal.archives-ouvertes.fr/hal-01209967

Google Scholar

Van Ooijen, J., Boer, M., Jansen, R., and Maliepaard, C. (2002). MapQTL 4.0, Software for the Calculation of QTL Positions on Genetic Maps. Wageningen: Plant Research International.

Google Scholar

Virlet, N., Lebourgeois, V., Martinez, S., Costes, E., Labbé, S., and Regnard, J.-L. (2014). Stress indicators based on airborne thermal imagery for field phenotyping a heterogeneous tree population for response to water constraints. J. Exp. Bot. 65, 5429–5442. doi: 10.1093/jxb/eru30

PubMed Abstract | CrossRef Full Text | Google Scholar

Vos, J., Evers, J. B., Buck-Sorlin, G. H., Andrieu, B., Chelle, M., and de Visser, P. H. B. (2010). Functional–structural plant modelling: a new versatile tool in crop science. J. Exp. Bot. 61, 2101–2115. doi: 10.1093/jxb/erp345

PubMed Abstract | CrossRef Full Text | Google Scholar

Whittaker, J. C., Thompson, R., and Denham, M. C. (2000). Marker-assisted selection using ridge regression. Genet. Res. 75, 249–252. doi: 10.1017/S0016672399004462

CrossRef Full Text | Google Scholar

Wu, R., and Stettler, R. F. (1994). Quantitative genetics of growth and development in Populus. I. A three-generation comparison of tree architecture during the first 2 years of growth. Theor. Appl. Genet. 89, 1046–1054. doi: 10.1007/BF00224537

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, R. L. (1998). Genetic mapping of QTLs affecting tree growth and architecture in Populus: implication for ideotype breeding. Theor. Appl. Genet. 96, 447–457. doi: 10.1007/s001220050761

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, L., and Buck-Sorlin, G. (2016). “Simulating genotype-phenotype interaction using extended functional-structural plant models: approaches, applications and potential pitfalls,” in Crop Systems Biology, eds X. Yin and P. C. Struik (Cham: Springer International Publishing), 33–53. doi: 10.1007/978-3-319-20562-5_2

CrossRef Full Text | Google Scholar

Xu, L., Ding, W., Henke, M., Kurth, W., Zhu, J., and Buck-Sorlin, G. (2012). “Simulating superior genotypes for plant height based on QTLs: towards virtual breeding of rice,” in Proceedings of the IEEE International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications, ed. M. G. Kang, Y. Dumont, and Y. Guo (Shangai: IEEE), 447–454.

Google Scholar

Xu, L., Henke, M., Zhu, J., Kurth, W., and Buck-Sorlin, G. (2011). A functional–structural model of rice linking quantitative genetic information with morphological development and physiological processes. Ann. Bot. 107, 817–828. doi: 10.1093/aob/mcq264

PubMed Abstract | CrossRef Full Text | Google Scholar