- 1Division of Genetics, ICAR-Indian Agricultural Research Institute, New Delhi, India
- 2Centre for Agricultural Bioinformatics, ICAR-Indian Agricultural Statistics Research Institute, New Delhi, India
- 3Office of Director General, Borlaug Institute for South Asia, New Delhi, India
Traditional breeding strategies for selecting superior genotypes depending on phenotypic traits have proven to be of limited success, as this direct selection is hindered by low heritability, genetic interactions such as epistasis, environmental-genotype interactions, and polygenic effects. With the advent of new genomic tools, breeders have paved a way for selecting superior breeds. Genomic selection (GS) has emerged as one of the most important approaches for predicting genotype performance. Here, we tested the breeding values of 240 maize subtropical lines phenotyped for drought at different environments using 29,619 cured SNPs. Prediction accuracies of seven genomic selection models (ridge regression, LASSO, elastic net, random forest, reproducing kernel Hilbert space, Bayes A and Bayes B) were tested for their agronomic traits. Though prediction accuracies of Bayes B, Bayes A and RKHS were comparable, Bayes B outperformed the other models by predicting highest Pearson correlation coefficient in all three environments. From Bayes B, a set of the top 1053 significant SNPs with higher marker effects was selected across all datasets to validate the genes and QTLs. Out of these 1053 SNPs, 77 SNPs associated with 10 drought-responsive transcription factors. These transcription factors were associated with different physiological and molecular functions (stomatal closure, root development, hormonal signaling and photosynthesis). Of several models, Bayes B has been shown to have the highest level of prediction accuracy for our data sets. Our experiments also highlighted several SNPs based on their performance and relative importance to drought tolerance. The result of our experiments is important for the selection of superior genotypes and candidate genes for breeding drought-tolerant maize hybrids.
Introduction
Traditional breeding strategies for selecting improved and resistant varieties of maize depending on the phenotypic trait have proven to be of limited success (Cushman and Bohnert, 2000). This direct selection is hindered by low heritability, and the existence of genetic interaction (e.g., epistasis), environmental-genotype interaction, and polygenic effects. This selection also takes a long period of time. Understanding the genetic basis of the plants' response to these various environments and the advent of new genomic technique and tools has allowed breeders to pave a way for selecting superior maize breeds (Tuberosa and Salvi, 2006).
Drought stress has the most detrimental effect on maize, leading to reduced yields in maize production (Nepolean et al., 2014). Several QTLs have been identified for drought tolerance in maize and those QTLs have been used to improve stress tolerance through marker-assisted breeding. However, marker-assisted breeding is limited to few major QTLs, thus minor QTLs are not part of the selection process, leading to a loss of genetic gain (Dekkers, 2004). To overcome this limitation, genomic selection (GS) has been proposed as a method to understand the effects of all the alleles across the genome to improve polygenic traits (Meuwissen et al., 2001). This method is advantageous over the traditional marker-assisted selection (MAS), as it addresses the effect of small genes which cannot be captured by the traditional MAS (Hayes et al., 2009).
GS is a form of MAS based on breeding values estimated from a genomic dataset that explores the genetic variances within each individual (Heffner et al., 2009). Current research in the area of genetic improvement explores GS as one of the approaches revolutionizing both animal and plant breeding (Hayes et al., 2009; Lorenzana and Bernardo, 2009). Genetic values of quantitative traits in maize and wheat datasets have been studied for the estimation of their higher predictive ability compared with molecular markers than pedigree information (Crossa et al., 2010).
GS reduced the selection time by almost half per cycle compared to the phenotypic selection for almost all traits in the different sets of maize, Arabidopsis and barley (Lorenzana and Bernardo, 2009). By replacing the phenotypic selection with the genomic estimated breeding value (GEBV), the gain for each unit cycle can be increased (Wong and Bernardo, 2008). GS can be appropriate even in the presence of modest molecular markers and diverse environmental conditions (Crossa et al., 2010). The prediction accuracy of breeding values in genomic selection has been found to be 0.58 for grain yield in maize (Zhao et al., 2012) and is estimated to be a better option than other methods considering the genetic gain each year (Lorenzana and Bernardo, 2009; Zhao et al., 2012).
Parametric (RR- Ridge Regression, LASSO- Least Absolute Shrinkage and Selection Operator, Elasticnet, Bayes A and Bayes B), semi parametric (RKHS- Reproducing Kernel Hilbert Space) and non-parametric (RF-Random Forest) models have been used to predict the genotype value, and machine learning programs (Long et al., 2007) have been proposed to develop prediction models for GS. These methods have been implemented in biparental (Lorenzana and Bernardo, 2009) and multi-parental populations (Heffner et al., 2011a) where the predictive ability using several models was compared among different datasets using Arabidopsis, wheat, maize, and barley.
Different genomic selection models have been examined in diverse panels of maize and wheat germplasm (De Los Campos et al., 2009; Crossa et al., 2010). GS contributed appreciable genetic gain for grain yield and stover quality in bi-parental maize population (Massman et al., 2013) and drought stress tolerance in tropical maize germplasm (Beyene et al., 2015). In maize, prediction accuracy of GS among the full-sibs was more accurate than unrelated crosses (Riedelsheimer et al., 2013). Among the GS models, rrBLUP and BSSV were found equally efficient in identifying the Stenocarpella maydis resistant maize inbred lines using DArTseq markers (Pedroso et al., 2016).
Little information exists in comparing the efficiency of genomic models to select the better genotypes for drought tolerance in subtropical maize germplasm. The objectives of the present investigation were to predict the GEBVs of genotypes under drought stress using seven GS models, to compare the prediction accuracies of those GS models, and to validate the top selected SNPs from GS models with the SNPs identified through previous GWAS experiment.
Materials and Methods
Dataset
A set of 29619 cured SNPs, genotyped across a panel of 240 maize inbred lines from an earlier data set (Nepolean et al., 2013, 2014) was used in this experiment. The curation of dataset was done on the basis of MAF <0.05, heterozygosity > 5%, removal of “no calls” (SNPs not included in any cluster were categorized as “no calls”), monomorphs and unmapped SNPs. Briefly, the total genomic DNA from 240 genotypes was isolated with a Nucleopore DNA Sure Plant Mini Kit (Genetix Biotech Asia). SNP detection was performed using the Infinium HD Assay Ultra (Illumina, San Diego, CA, USA). SNP chips were hybridized with 50 ng × 4 μl DNA per sample. The Maize SNP50 BeadChip was used to scan the 240 samples with 24 samples per Sentrix Array Matrix (SAM). All 240 genotypes were genotyped with an Infinium Maize SNP50 BeadChip (Illumina, San Diego, California, USA) containing 56110 SNPs.
Phenotypic data under drought stress in three different environments (IARI, New Delhi: 28°N 77°E; 229m AMSL), ANGRAU, Hyderabad: 17°N 78°E; 536m AMSL and RRS, Karimnagar: 18°N 79°E; 264m AMSL) during post-rainy seasons of 2010/11 and 2011/12 generated earlier (Nepolean et al., 2014) were used for predicting the GEBV in the current experiment. The “mean data” obtained by pooling datasets of these 3 locations was also included in the present experiment. All the drought experiments was followed the alpha lattice design consists of 16 incomplete blocks, and each block comprised of 15 plots with 3 replicates. Drought trials were phenotyped for the anthesis-to-silking interval (ASI, in days), the grain yield (GY, kilograms per plot), the number of kernels per row (KR), the number of kernel rows (KRN), the ear girth (EG, in centimeters), the ear length (EL, in centimeters), and the 100-kernel weight (HKW, in grams). Mean data across location for each genotype was calculated using the restricted maximum likelihood (ReML) approach and the best linear unbiased predictors (BLUPs) was used for further analysis.
Genomic Selection Models
Parametric models (RR, LASSO, EN, Bayes A, Bayes B), a non-parametric model (RF) and a semi-parametric model (RKHS) were used to estimate the genetic value of each genotype. Common variance was considered for all the markers by the ridge regression model (Meuwissen et al., 2001) and, therefore, for each marker effect it constricts uniformly. Estimation of RR βs was performed by minimizing the L2 panelized residual sum of squares (Riedelsheimer et al., 2012), where RR shrinks all marker effects toward zero rather than categorizing the markers as either significant or as having no effect (Breiman, 1995; Whittaker et al., 2000).
Another parametric model, LASSO, which estimates of the number of βs, was obtained by minimizing the residual sum of squares, and subjected to the constraint of L1-type penalty on regression coefficients (Technow et al., 2012). EN is a more generalized model that combines both the RR and LASSO penalties. EN's estimate of the number of βs was obtained by minimizing the residual sum of squares subjected to the constraints of both L1- and L2-type penalties on regression coefficients.
EN simplifies to RR when α = 1 and to LASSO when α = 0. For any other value of α (0 < α <1), EN is used. The L1 part of EN performs automatic variable selection while L2executes grouped selection and stabilizes the solution paths with respect to random sampling. Predictive accuracies and significant SNPs for all traits were estimated through RR, LASSO, and EN with the use of an R package “glmnet” with penalty parameters optimized via ten-fold cross validation (Friedman et al., 2010). The significant SNPs estimated on the basis of variable importance were compared with the previous genome-wide association (GWA) results from the water-stressed maize panels (Nepolean et al., 2014).
The other two parametric models, Bayes A and Bayes B (Meuwissen et al., 2001) do not consider the common variance across the effects of SNPs. The Gibbs sampler for 50,000 repetitions fitting the model was computed by discarding the first 5,000 samples as a burn-in and saving one of each of the ten samples for computing the posterior means for parameters. The Bayes A method assumes conditional distribution of each marker effect (given its variance) to follow a normal distribution. If the π value becomes zero, then the Bayes B model shrinks to Bayes A. We used the “BGLR” R package for the implementation of both Bayes A and Bayes B (De Los Campos et al., 2013).
A kernel function is used by the RKHS method to translate datasets of markers into a square matrix to be used in a linear model. There is a possibility that this method might capture non-additive genetic effects because of its ability to perform non-linear regression in a higher dimensional space. RKHS prediction was performed using “BGLR” (Bernardo and Yu, 2007). The model can be formulated as follows:
where ε can be defined as a vector of random residuals and μ as a vector of fixed effects. The parameters α and ε have independent distributions. The matrix Kh depends on a kernel function with the smoothing parameter h, which measures the “genomic distance” between genotypes and can be interpreted as a correlation matrix. The “genomic distance” between genotypes is measured by Kh, where h represents the smoothing parameter and can be elucidated as a correlation matrix. Here, the Gaussian kernel was used on the genetic distance. The decay rate of correlation between genotypes is regulated by the h parameter.
Genomic prediction using parametric and semi-parametric models RR, LASSO, EN, Bayes A, Bayes B, and RKHS was based on 29,619 SNPs, while prediction using a non-parametric model Random Forest (RF) was performed using 5420 SNPs that were randomly selected from a set of 29,619 SNPs. The RF test uses a random subset of predictors to form a collection of regression trees on the basis of bootstrap samples of observations. This model was implemented using the R package “RandomForest” (Liaw and Wiener, 2002) where the number of trees was adjusted to 1,000, keeping mtry at p/3. Prediction accuracy for all agronomic traits was calculated through “Pearson correlation coefficient” between observed and predicted value in all seven GS models.
Validation
To compute predictive accuracies, a 10-fold cross-validation (CV) scheme was applied and iterated 10 times. In each iteration, 10 disjoint subsets of genotypes were formed randomly where one random subset was used as a validation set and the other nine subsets were used as a training population to estimate the parameters of the model used for prediction of excluded genotypes in the validation set. The Pearson correlation between observed and predicted values was calculated in each round. This procedure was iterated 10 times to obtain 100 cross-validation runs. The predictive ability was calculated as the Pearson correlation coefficient between observations and cross-validated GEBVs were thus referred for accuracy.
Results
Mean Performance
Under drought condition, the performance of 7 agronomic traits—ASI, GY, KR, KRN, EG, EL, and HKW were recorded in all three locations. In summary, the mean data from all three locations explained that ASI under drought varied from 2 to 12 days with a mean value of 6 days and standard deviation of 2.53. GY had a range of 0.2–2.2 with an average of 1.7 and a standard deviation 1.92. For KRN, the mean and standard deviation was 31 and 2.57, respectively. Other agronomic traits i.e., EL, EG, KR, and HKW, the range varied from 7.8–17.5, 1.8–4.1, 10.9–18 and 15–32 with an average of 13.4, 3.3, 13, and 26 respectively (Nepolean et al., 2014).
Prediction Accuracy of GS Models
Accuracy of the seven GS models was predicted for all seven traits phenotyped for drought stress at the three locations (Table 1). While comparing the prediction accuracies among these traits and locations, we observed that the highest prediction accuracies of 0.93, 0.91, and 0.92 were identified for ASI, EG, and HKW, respectively, in Karimnagar, whereas for GY, Hyderabad and Karimnagar provided the best results, and Karimnagar and IARI showed better results than Hyderabad for EL. The highest prediction accuracy for KRN was identified in Hyderabad with a value of 0.91. KR was the only trait in which all the 3 locations provided consistent results. Across all traits, the maximum prediction accuracy was found for ASI and the minimum for KR. It was examined that among the 3 locations, Karimnagar provided the best results.
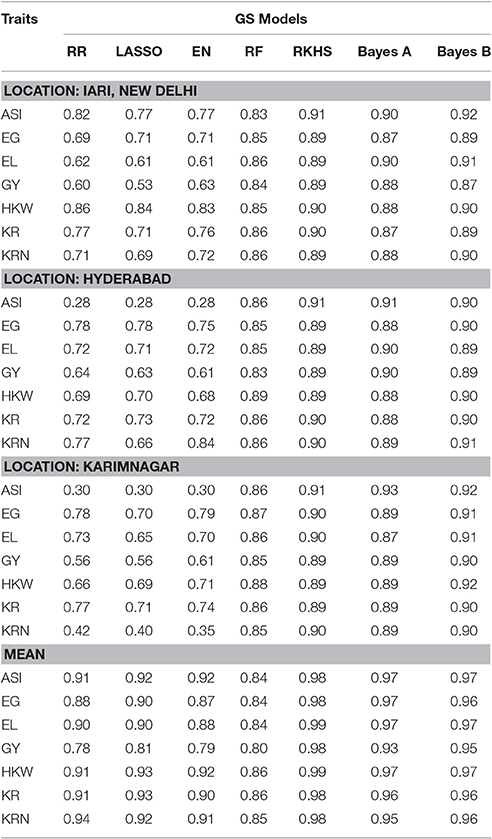
Table 1. Prediction accuracies of agronomic traits predicted by seven GS models under drought stress in subtropical maize.
Prediction accuracy and standard deviations ranged between 0.28–0.92 and 0.03–0.06 (Hyderabad), 0.53–0.92 and 0.02–0.06 (IARI), and 0.30–0.93 and 0.02–0.06 (Karimnagar), respectively, across all traits and models. RKHS, Bayes A, and Bayes B showed no difference in the prediction accuracy above 0.04, while RR, LASSO and EN showed prediction accuracies above 0.03 for all traits, except for KRN, which showed a difference of more than 0.07 at all locations. Bayes B estimated the highest prediction accuracy for all traits except for EG and KRN. Bayes A and RKHS provided the second best prediction accuracy with a drop of 0.01–0.02 (Hyderabad); 0.01–0.03 (IARI), except for GY; and 0.01–0.04 (Karimnagar), except for ASI, respectively, compared to Bayes B.
A great fall in the prediction accuracies for certain traits (ASI, GY, and KRN) under specific models over different locations was observed. Ridge, lasso and EN models predicted ASI with less accuracy (0.28) in Hyderabad. Similarly, in IARI, less prediction accuracy was found for GY (0.6), whereas Karimnagar, ASI (0.3), GY (0.56), and KRN (0.4) had less accuracy compared to the other traits and locations. For GY, the best results (0.9) for Hyderabad and Karimnagar were predicted by both Bayes A and Bayes B, while for IARI, RKHS predicted the best value (0.89). Overall, the prediction accuracy of the mean location was better than that for individual locations.
In location-wise comparison, it was noticed that though the results of RKHS, Bayes A and Bayes B were quite similar but the highest prediction accuracy was obtained from the Bayes B model in all 3 locations namely Hyderabad, IARI and Karimnagar while in the mean dataset RKHS was slightly better over the Bayes B.
SNPs Identified through Different Models
We had estimated the prediction accuracy for seven GS models. From these models, the Bayes B model provided the maximum accuracy for six of the seven traits across several environments. A set of the top 100 SNPs with the highest marker effect observed in each trait and environment was selected using the Bayes B since it produced highest accuracy in all three locations. From this exercise, a total of 2800 SNPs with the highest marker effect across several datasets (traits + environments) were identified. Out of these SNPs, 1053 SNPs were unique (Supplementary Table S1). These SNPs distributed across the genome, ranging from 52 SNPs in chromosome 2–150 SNPs in chromosome 1 (Figure 1).
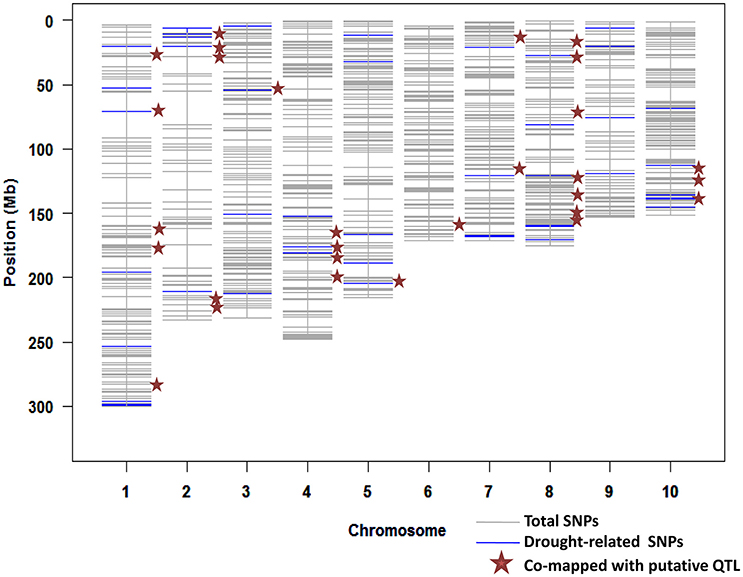
Figure 1. Distribution of SNPs with higher marker effects mapped for different traits and locations from the Bayes B model; several SNPs were associated with drought-related transcription factors and co-mapped with putative QTLs.
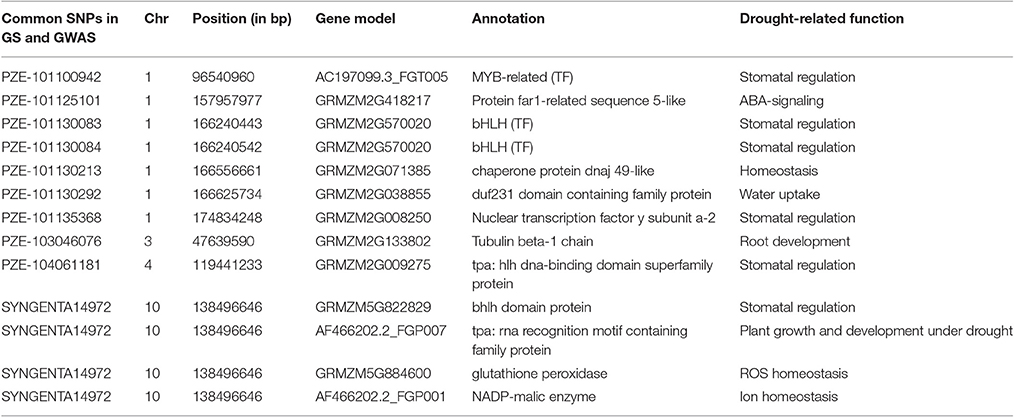
Out of the 1053 SNPs, a set of 77 consistent SNPs identified across several traits and locations (Table 2) were selected as a test for understanding their functional relationships with drought-tolerant genes. The maize gene models explained that these 77 SNPs distributed across the genome were mapped 10 drought-responsive TFs within their 150 Kb region. CAMTA mapped within 41 Kb region followed by bHLH (73 Kb), bZIP (92 Kb), NF-YB (101 Kb), NF-YA (108 Kb), GRAS (120 Kb), WRKY (125 Kb), AP2-ERF (148 Kb), MYB (149 Kb), and NAC (149 Kb). The AP2-ERF TF family was mapped close to the maximum number of SNPs (30) on all chromosomes; whereas chromosome 9 had the most drought-responsive SNPs (6) and chromosome 3 contributed only one drought-responsive SNP. The MYB TF family was mapped to 17 SNPs located on all chromosomes except on chromosomes 1 and 10. The SNP PZE-109076471 on chromosome 9 was mapped 2 Kb from MYB TF. Both WRKY and GRAS TFs mapped 10 unique and seven SNPs in their vicinity, respectively. The BHLH TF family encompassed five SNPs on different chromosomes, including an SNP (PZE-110088632) on chromosome 10, which was located only 732 bp away from the BHLH TF. The NF-YA (3), bZIP (2), NAC (1), CAMTA (1), and NF-YB (1) TFs mapped 3, 2, 1, and 1 SNPs, respectively. In addition, SNPs were also mapped close to more than one TF family. The SNP SYN38859 on chromosome 2 was mapped close to MYB and AP2-ERF at a distance of 2 and 116 Kb away, respectively, and another SNP (PZE-107128846) on chromosome 7 was mapped at a distance of 54 and 108 Kb away from the GRAS and NF-YA TFs, respectively.
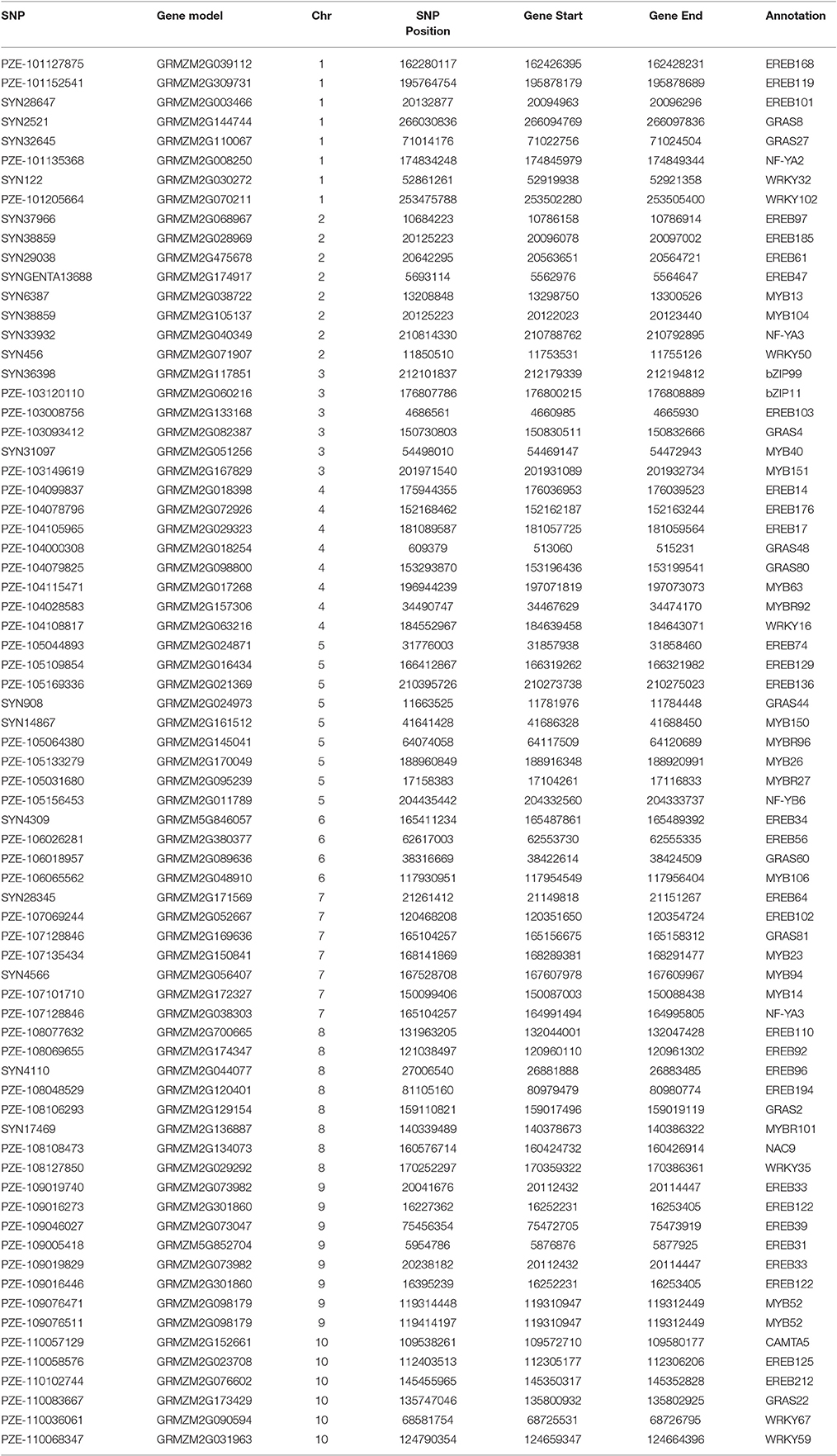
Table 2. A set of 77 consistent SNPs identified through Bayes B mapped drought-responsive transcription factors within the 150 Kb region.
The set of 1053 SNPs detected using the Bayes B model were matched with the previously identified 67 significant SNPs from GWAS models of GenABEL and GAPIT (Nepolean et al., 2014). We found 10 SNPs which were commonly identified by GS as well as GWAS models (Table 3). These SNPs were mapped on different chromosomes i.e., chromosome 1 (7 SNPs), chromosome 3 (1 SNP), chromosome 4 (1 SNP), and chromosome 10 (1 SNP). All these SNPs were associated with 13 maize gene models and had drought-related functions. Six SNPs were annotated as transcription factors including MYB, bHLH, NF-YA, and FAR1 while rest of them as chaperone protein dnaj 49-like, duf231 domain containing family protein, tubulin beta-1 chain, glutathione peroxidase, and NADP-malic enzyme.
Discussion
Many studies have implemented GS to test the gains in various genetic enhancement programs (Bernardo and Yu, 2007; Wong and Bernardo, 2008; Mayor and Bernardo, 2009; Shengqiang et al., 2009). A high level of correlation between true breeding values and the GEBV is found to be sufficient for genomic selection based on marker data (Heffner et al., 2009).
Different approaches have been used to determine breeding values from GS models–penalized regressions (RR, LASSO, and EN), Bayesian approaches (Bayes A and Bayes B), and non-linear regressions (RKHS and RF) (Hayes et al., 2009; Heslot et al., 2012; Nepolean et al., 2013). Non-linear regression models are studied for higher prediction accuracy over penalized models. In our study, we found higher prediction accuracy for both non-linear models compared to penalized models, with a maximum difference of 0.25 between non-linear models and penalized models across all seven traits. Among several different GS models, a better accuracy is found for non-linear models since they can capture non-additive genetic effects (Technow et al., 2012). However, if the additive genetic effects are solely included, using nonparametric models may not yield the expected level of accuracy.
The least prediction accuracy was observed for regularized linear models in this study. This model can be supported by the presence of epistatic interactions which may lower the performance of linear models (Ogutu et al., 2012). Among the penalized models, we observed better prediction accuracy for EN and RR than for LASSO. These results were in agreement with a previous study where EN outperformed LASSO in terms of consistency of model selection and prediction accuracy (Zou and Hastie, 2005).
Bayes B is a variable selection operator, and identifies a subset of markers with larger effects particularly those controlled by a few large QTLs. In our study, the Bayes B approach provided better prediction accuracy across all data (location + trait) compared to other GS models. Previous studies have also reported the better performance of Bayes B as compared to other GS models (VanRaden et al., 2009; Daetwyler et al., 2010; Jannink et al., 2010). We also observed that RKHS showed the highest prediction accuracy but was restricted to a few datasets. The variation in prediction superiority for RKHS has also been observed in previous results (Shengqiang et al., 2009; Crossa et al., 2010). The Bayesian model incorporates additive genetic effects, while RKHS captures complex epistatic interactions (Gianola and Van Kaam, 2008). Therefore, one would expect the Bayesian method to perform well in traits where additive effects play a central role and RKHS to perform well in traits where epitasis is more relevant. This also implied that both additive and non-additive components play significant role in trait expression in variable magnitude depending upon the genetic architecture of the traits (Crossa et al., 2010).
Our results showed the presence of variation in predicting the breeding values in different locations which explained that breeding values are shaped up by the environment. The results were also in coherent with our previous GWAS results (Nepolean et al., 2014) where location-specific SNPs were identified. It is also interesting to note that several SNPs were consistent in across locations as well as across traits in the GWAS study.
Genotype × Environment (G × E) interaction is an important component of genetic variability (Crossa et al., 2010, 2011). Various genomic selection studies have included G × E effect while predicting the values in across environments (Heffner et al., 2011b; Resende et al., 2011), within environments or group of environments (Burgueño et al., 2012; Dawson et al., 2013; Ly et al., 2013; Heslot et al., 2014) or using marker-by-environment predictions (Jarquín et al., 2014; Lopez-Cruz et al., 2015).
In our experiment, the Bayesian models out-performed the RR and LASSO models, and this result may be because Bayesian models utilize marker-specific shrinkage of effects, while RR and LASSO equally penalize entire marker effects (Meuwissen et al., 2001). This effect was evident in this study where Bayesian models out-performed the BLUP model by a difference of 0.25 in prediction accuracies. The latter model considers equal variance in all markers, and does not require preliminary information on the variance of marker effects. However, this information is required in Bayesian approaches to estimate prediction accuracies. In addition, RR also incorporates familial relationships and is hence inferior to Bayesian method (Habier et al., 2007). Since the Bayes B method estimates higher prediction accuracies for six of seven traits, it was selected for further validation of SNPs associated with drought tolerance.
Functional Mechanisms of Selected Top SNPs
The SNPs selected based on their marker effects were found to be associated with 10 droughts responsive TFs. The collective role and the interaction of those SNPs with various stress-related mechanisms at a functional level are discussed below.
Hormone Signaling
Abscisic acid (ABA) is a phytohormone stimulated in response to developmental and environmental stimuli. Early stages in ABA signaling involve ABA receptors, phosphatases, and kinases that control the regulation of their targets (Soon et al., 2012). The binding of ABA molecules to their receptors stimulates the inhibition of proteinphosphatases (PP2Cs), which, in turn activates SNF1-related protein kinase 2 (SnRK2) (Ng et al., 2011; Soon et al., 2012). SnRK2 is an important signaling molecule that phosphorylates its downstream targets, including the transcription factors NAC, bZIP, HSF, MYB, WRKY, and RAV1 (belonging to AP2-ERF family; Furihata et al., 2006; Fujita et al., 2009; Kim et al., 2012; Feng et al., 2014). ABA-inducible bZIP transcription factors containing ABA-responsive elements (ABRE) regulate HSFs in a drought-responsive manner (Yoshida et al., 2010; Bechtold et al., 2013).
Under drought stress, ABA is accumulated in guard cells where the closing of stomata is dependent upon H2O2 synthesis produced in the ABA-signaling pathway (Bright et al., 2006). Drought-inducible transcription factors WRKY (Ren et al., 2010), NF-YA (Gao et al., 2015), MYB (Seo and Park, 2009), CAMTA (Pei et al., 2000; Chen et al., 2004; Pandey et al., 2013), C2H2 (Huang et al., 2009) and bHLH (Abe et al., 2003; Seo et al., 2011) trigger stomatal closure under the effect of ABA alone in drought stress. ERF is another drought-responsive transcription factor stimulated under the effect of ABA but is also integrated with other two hormones—jasmonic acid and ethylene—which induce the closing of stomata (Cheng et al., 2013). The ERF transcription factor mapped close to three SNPs, distributed on chromosomes 5, 7, and 8 was co-localized with quantitative trait loci (QTLs) mapped for EL, GY, ASI, and KRN in earlier studies (Guo et al., 2008; Messmer et al., 2009; Nikolić et al., 2012; Figure 2).
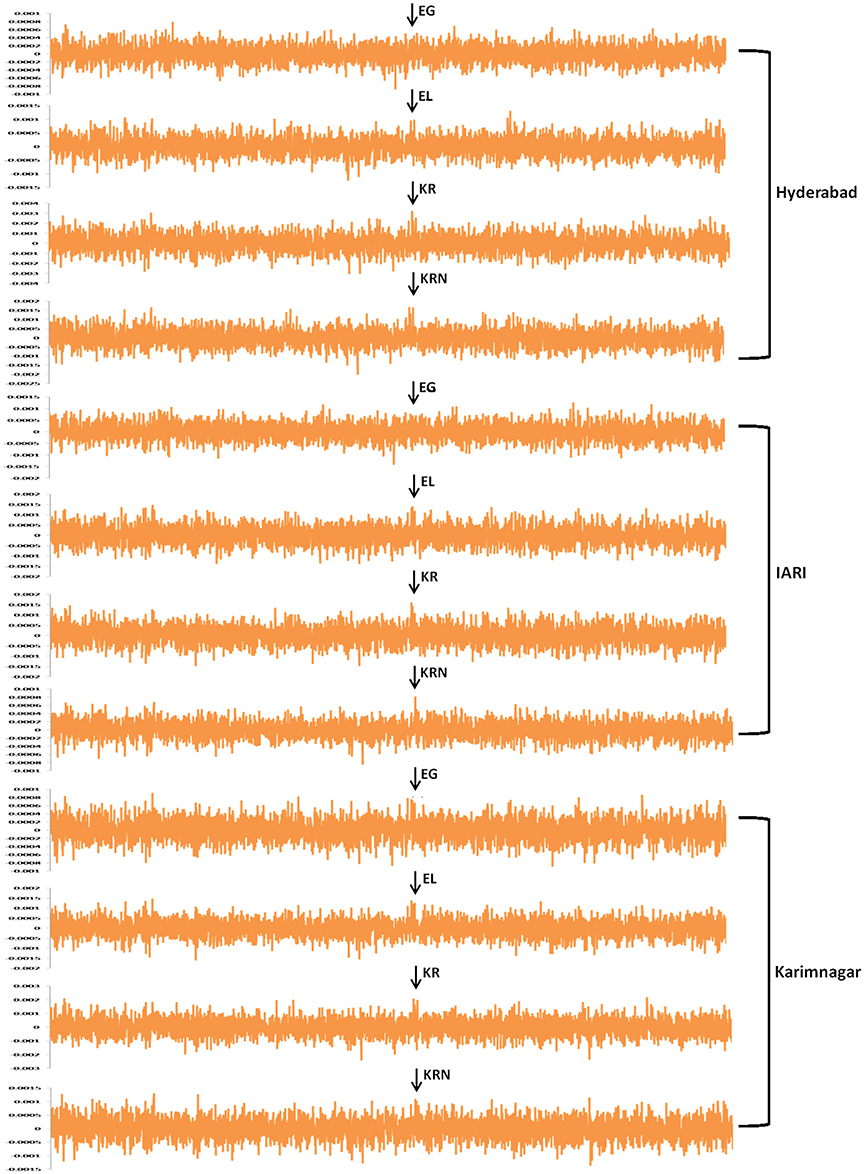
Figure 2. The marker effect of a consistent SNP PZE-104079825 associated with the ROS scavenging GRAS transcription factor mapped on chromosome 4 from various traits and locations.
Gibberellic acid is another plant hormone that promotes growth and cellular elongation; however, its impact on drought stress is not completely understood. GA-responsive transcription factors such as SCARECROW (belonging to GRAS family) are studied for their involvement in cellular differentiation in the Arabidopsis root meristem (Sabatini et al., 2003; Ma et al., 2010). These plant hormones constitute a signaling network that involves various receptors, phosphatases, kinases, calcium-binding signaling molecules, and transcription factors.
Photosynthesis
Maintenance of photosynthesis is an adaptive trait that contributes to an improvement in grain yield in drought stressed plants. The transgenic maize with an increased NF-YB activity is studied for drought tolerance with a maintained photosynthetic rate and high yield (Nelson et al., 2007). These plants also showed good stomatal conductance and high chlorophyll index in water stressed conditions. In addition, the NF-YB transcription factor mapped close to an SNP on chromosome 5 and was co-localized with a QTL for GY, which was previously identified by Nikolić et al. (2012). Another transcription factor CAMTA is identified as a regulator of the photosynthetic machinery, where the T-DNA insertion line of AtCAMTAs has low photo system II efficiency under drought stress (Pandey et al., 2013).
Root Development
A deeper root system is capable of accessing all soil moisture in a drought-stressed plant system. Root development due to drought tolerance has been observed in SNAC1-overexpressing transgenic cotton plants (Liu et al., 2014), and root enlargement has been observed in root-overexpressing OsNAC10 drought-stressed rice plants (Jeong et al., 2010). However, the inhibition of lateral root development is an adaptive response to drought stress (Xiong et al., 2006), whereas reduced lateral root formation and improved drought tolerance have been found in Arabidopsis MYB96-overexpressing mutant plants (Seo and Park, 2009).
Conclusion
Our results showed that Bayes B is superior to the other GS models in predicting the genomic values of the studied genotypes. Using Bayes B, we found 77 SNPs that are significant by their marker effects and are related to drought-responsive TFs. We also identified common SNPs from current GS model and previous GWAS models. These significant SNPs are related to many functions, such as stomatal closure, root development, hormonal signaling and photosynthesis. As these SNPs are drought-related and involved in various molecular functions, they can be further used for the development of drought-tolerant hybrids.
Availability of Supporting Data
The raw SNP data (Submission No. 10.6070/H4BG2KX8) have been submitted to the website http://www.labarchives.com/. All other supporting data are included as additional files.
Author Contributions
TN and HSG conceived and designed the experiments; MS, AK, ARR, MGM, and TN analyzed the data. TN, MS, and AK drafted the manuscript. All authors read and approved the final manuscript.
Funding
The experiment was funded by the National Agricultural Innovation Project (NAIP, Component IV), the ICAR Network Project on Transgenics in Crop Plants (Maize Functional Genomics Component), and Computational Biology and Agricultural Bioinformatics (Agril.Edn.14(44)/2014-A&P). The funding agencies had no role in the study design, data collection and analysis, the decision to publish, or the preparation of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer DS and handling Editor declared their shared affiliation, and the handling Editor states that the process nevertheless met the standards of a fair and objective review.
Acknowledgments
We profusely thank the plant breeders from various breeding centers in India and from CIMMYT for providing the seeds and for generating the primary genotyping and phenotyping data.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fpls.2017.00550/full#supplementary-material
Abbreviations
GS, Genomic selection; RR, Ridge regression; LASSO, Least Absolute Shrinkage and Selection Operator; EN, Elastic Net; RF, Random Forest; RKHS, Reproducing Kernel Hilbert Space; MAS, Marker Assisted selection; QTL, Quantitative trait loci; GEBV, genomic estimated breeding value; SNP, Single nucleotide polymorphism; ASI, anthesissilking Interval; GY, Grain yield; KR, number of kernels per row; KRN, number of kernel rows; EG, Ear girth; EL, Ear length; HKW, 100 kernel weight; GWA, genome wide association; CV, cross-validation; TF, Transcription factor.
References
Abe, H., Urao, T., Ito, T., Seki, M., Shinozaki, K., and Yamaguchi-Shinozaki, K. (2003). Arabidopsis AtMYC2 (bHLH) and AtMYB2 (MYB) function as transcriptional activators in abscisic acid signaling. Plant Cell 15, 63–78. doi: 10.1105/tpc.006130
Bechtold, U., Albihlal, W. S., Lawson, T., Fryer, M. J., Sparrow, P. A. C., Richard, F., et al. (2013). Arabidopsis HEAT SHOCK TRANSCRIPTION FACTORA1b overexpression enhances water productivity, resistance to drought, and infection. J. Exp. Bot. 64, 3467–3481. doi: 10.1093/jxb/ert185
Bernardo, R., and Yu, J. (2007). Prospects for genomewide selection for quantitative traits in maize. Crop Sci. 47, 1082–1090. doi: 10.2135/cropsci2006.11.0690
Beyene, Y., Semagn, K., Mugo, S., Tarekegne, A., Babu, R., Meisel, B., et al. (2015). Genetic gains in grain yield through genomic selection in eight bi-parental maize populations under drought stress. Crop Sci. 55, 154–163. doi: 10.2135/cropsci2014.07.0460
Breiman, L. (1995). Better subset regression using the nonnegative garotte. Technometrics 37, 373–384.
Bright, J., Desikan, R., Hancock, J. T., Weir, I. S., and Neill, S. J. (2006). ABA-induced NO generation and stomatal closure in Arabidopsis are dependent on H2O2 synthesis. Plant J. 45, 113–122. doi: 10.1111/j.1365-313X.2005.02615.x
Burgueño, J., de los Campos, G., Weigel, K., and Crossa, J. (2012). Genomic prediction of breeding values when modeling genotype × environment interaction using pedigree and dense molecular markers. Crop Sci. 52, 707–719. doi: 10.2135/cropsci2011.06.0299
Chen, Y.-L. Y., Huang, R., Xiao, Y.-M. Y., Lü, P., Chen, J., and Wang, X.-C. (2004). Extracellular calmodulin-induced stomatal closure is mediated by heterotrimeric G protein and H2O2. Plant Physiol. 136, 4096–4103. doi: 10.1104/pp.104.047837
Cheng, M.-C., Liao, P.-M., Kuo, W.-W., and Lin, T.-P. (2013). The Arabidopsis ETHYLENE RESPONSE FACTOR1 regulates abiotic stress-responsive gene expression by binding to different cis-acting elements in response to different stress signals. Plant Physiol. 162, 1566–1582. doi: 10.1104/pp.113.221911
Crossa, J., De Los Campos, G., Pérez, P., Gianola, D., Burgueño, J., Araus, J. L., et al. (2010). Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 186, 713–724. doi: 10.1534/genetics.110.118521
Crossa, J., Pérez, P., de los Campos, G., Mahuku, G., Dreisigacker, S., and Magorokosho, C. (2011). Genomic selection and prediction in plant breeding. J. Crop Improv. 25, 239–261. doi: 10.1080/15427528.2011.558767
Cushman, J. C., and Bohnert, H. J. (2000). Genomic approaches to plant stress tolerance. Curr. Opin. Plant Biol. 3, 117–124. doi: 10.1016/S1369-5266(99)00052-7
Daetwyler, H. D., Pong-Wong, R., Villanueva, B., and Woolliams, J. A. (2010). The impact of genetic architecture on genome-wide evaluation methods. Genetics 185, 1021–1031. doi: 10.1534/genetics.110.116855
Dawson, J. C., Endelman, J. B., Heslot, N., Crossa, J., Poland, J., Dreisigacker, S., et al. (2013). The use of unbalanced historical data for genomic selection in an international wheat breeding program. F. Crop. Res. 154, 12–22. doi: 10.1016/j.fcr.2013.07.020
Dekkers, J. C. (2004). Commercial application of marker- and gene-assisted selection in livestock: strategies and lessons. J. Anim. Sci. 82 (E-Suppl.):E313–E328.
De Los Campos, G., Naya, H., Gianola, D., Crossa, J., Legarra, A., Manfredi, E., et al. (2009). Predicting quantitative traits with regression models for dense molecular markers and pedigree. Genetics 182, 375–385. doi: 10.1534/genetics.109.101501
De Los Campos, G., Pataki, A., and Perez, P. (2013). Bayesian Generalized Linear Regression (BGLR). Available online at: https://cran.r-project.org/web/packages/BGLR/BGLR.pdf
Feng, C. Z., Chen, Y., Wang, C., Kong, Y. H., Wu, W. H., and Chen, Y. F. (2014). Arabidopsis RAV1 transcription factor, phosphorylated by SnRK2 kinases, regulates the expression of ABI3, ABI4, and ABI5 during seed germination and early seedling development. Plant J. 80, 654–668. doi: 10.1111/tpj.12670
Friedman, J., Hastie, T., and Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33, 1–22. doi: 10.1359/JBMR.0301229
Fujita, Y., Nakashima, K., Yoshida, T., Katagiri, T., Kidokoro, S., Kanamori, N., et al. (2009). Three SnRK2 protein kinases are the main positive regulators of abscisic acid signaling in response to water stress in Arabidopsis. Plant Cell Physiol. 50, 2123–2132. doi: 10.1093/pcp/pcp147
Furihata, T., Maruyama, K., Fujita, Y., Umezawa, T., Yoshida, R., Shinozaki, K., et al. (2006). Abscisic acid-dependent multisite phosphorylation regulates the activity of a transcription activator AREB1. Proc. Natl. Acad. Sci. U.S.A. 103, 1988–1993. doi: 10.1073/pnas.0505667103
Gao, W., Liu, W., Zhao, M., and Li, W. X. (2015). NERF encodes a RING E3 ligase important for drought resistance and enhances the expression of its antisense gene NFYA5 in Arabidopsis. Nucleic Acids Res. 43, 607–617. doi: 10.1093/nar/gku1325
Gianola, D., and Van Kaam, J. B. C. H. M. (2008). Reproducing kernel Hilbert spaces regression methods for genomic assisted prediction of quantitative traits. Genetics 178, 2289–2303. doi: 10.1534/genetics.107.084285
Guo, J., Su, G., Zhang, J., and Wang, G. (2008). Genetic analysis and QTL mapping of maize yield and associate agronomic traits under semi-arid land condition. African J. Biotechnol. 7, 1829–1838. doi: 10.5897/AJB2008.000-5031
Habier, D., Fernando, R. L., and Dekkers, J. C. M. (2007). The impact of genetic relationship information on genome-assisted breeding values. Genetics 177, 2389–2397. doi: 10.1534/genetics.107.081190
Hayes, B. J., Bowman, P. J., Chamberlain, A. J., and Goddard, M. E. (2009). Invited review: genomic selection in dairy cattle: progress and challenges. J. Dairy Sci. 92, 433–443. doi: 10.3168/jds.2008-1646
Heffner, E. L., Jannink, J. L., Iwata, H., Souza, E., and Sorrells, M. E. (2011a). Genomic selection accuracy for grain quality traits in biparental wheat populations. Crop Sci. 51, 2597–2606. doi: 10.2135/cropsci2011.05.0253
Heffner, E. L., Jannink, J., and Sorrells, M. E. (2011b). Genomic selection accuracy using multifamily prediction models in a wheat breeding program. Plant Genome 4, 65–75. doi: 10.3835/plantgenome2010.12.0029
Heffner, E. L., Sorrells, M. E., and Jannink, J. (2009). Genomic selection for crop improvement. Crop Sci. 49, 1–12. doi: 10.2135/cropsci2008.08.0512
Heslot, N., Akdemir, D., Sorrells, M. E., and Jannink, J. L. (2014). Integrating environmental covariates and crop modeling into the genomic selection framework to predict genotype by environment interactions. Theor. Appl. Genet. 127, 463–480. doi: 10.1007/s00122-013-2231-5
Heslot, N., Yang, H.-P., Sorrells, M. E., and Jannink, J.-L. (2012). Genomic selection in plant breeding: a comparison of models. Crop Sci. 52:146. doi: 10.2135/cropsci2011.09.0297
Huang, X.-Y., Chao, D.-Y., Gao, J.-P., Zhu, M.-Z., Shi, M., and Lin, H.-X. (2009). A previously unknown zinc finger protein, DST, regulates drought and salt tolerance in rice via stomatal aperture control. Genes Dev. 23, 1805–1817. doi: 10.1101/gad.1812409
Jannink, J.-L. L., Lorenz, A. J., and Iwata, H. (2010). Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9, 166–177. doi: 10.1093/bfgp/elq001
Jarquín, D., Crossa, J., Lacaze, X., Du Cheyron, P., Daucourt, J., Lorgeou, J., et al. (2014). A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor. Appl. Genet. 127, 595–607. doi: 10.1007/s00122-013-2243-1
Jeong, J. S., Kim, Y. S., Baek, K. H., Jung, H., Ha, S.-H., Do Choi, Y., et al. (2010). Root-specific expression of OsNAC10 improves drought tolerance and grain yield in rice under field drought conditions. Plant Physiol. 153, 185–197. doi: 10.1104/pp.110.154773
Kim, M. J., Park, M.-J., Seo, P. J., Song, J.-S., Kim, H.-J., and Park, C.-M. (2012). Controlled nuclear import of the transcription factor NTL6 reveals a cytoplasmic role of SnRK2.8 in the drought-stress response. Biochem. J. 448, 353–363. doi: 10.1042/BJ20120244
Liaw, A., and Wiener, M. (2002). Classification and Regression by randomForest. R news 2, 18–22. doi: 10.1177/154405910408300516
Liu, G., Li, X., Jin, S., Liu, X., Zhu, L., Nie, Y., et al. (2014). Overexpression of rice NAC gene SNAC1 improves drought and salt tolerance by enhancing root development and reducing transpiration rate in transgenic cotton. PLoS ONE 9:e86895. doi: 10.1371/journal.pone.0086895
Long, N., Gianola, D., Rosa, G. J. M., Weigel, K. A., and Avendaño, S. (2007). Machine learning classification procedure for selecting SNPs in genomic selection: application to early mortality in broilers. J. Anim. Breed. Genet. 124, 377–389. doi: 10.1111/j.1439-0388.2007.00694.x
Lopez-Cruz, M., Crossa, J., Bonnett, D., Dreisigacker, S., Poland, J., Jannink, J.-L., et al. (2015). Increased prediction accuracy in wheat breeding trials using a marker × environment interaction genomic selection model. G3 (Bethesda). 5, 569–582. doi: 10.1534/g3.114.016097
Lorenzana, R. E., and Bernardo, R. (2009). Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor. Appl. Genet. 120, 151–161. doi: 10.1007/s00122-009-1166-3
Ly, D., Hamblin, M., Rabbi, I., Melaku, G., Bakare, M., Gauch, H. G., et al. (2013). Relatedness and genotype × environment interaction affect prediction accuracies in genomic selection: a study in cassava. Crop Sci. 53, 1312–1325. doi: 10.2135/cropsci2012.11.0653
Ma, H. S., Liang, D., Shuai, P., Xia, X. L., and Yin, W. L. (2010). The salt-and drought-inducible poplar GRAS protein SCL7 confers salt and drought tolerance in Arabidopsis thaliana. J. Exp. Bot. 61, 4011–4019. doi: 10.1093/jxb/erq217
Massman, J. M., Jung, H. J. G., and Bernardo, R. (2013). Genomewide selection versus marker-assisted recurrent selection to improve grain yield and stover-quality traits for cellulosic ethanol in maize. Crop Sci. 53, 58–66. doi: 10.2135/cropsci2012.02.0112
Mayor, P. J., and Bernardo, R. (2009). Genomewide selection and marker-assisted recurrent selection in doubled haploid versus F2 populations. Crop Sci. 49, 1719–1725. doi: 10.2135/cropsci2008.10.0587
Messmer, R., Fracheboud, Y., Bänziger, M., Vargas, M., Stamp, P., and Ribaut, J. M. (2009). Drought stress and tropical maize: QTL-by-environment interactions and stability of QTLs across environments for yield components and secondary traits. Theor. Appl. Genet. 119, 913–930. doi: 10.1007/s00122-009-1099-x
Meuwissen, T. H. E., Hayes, B. J., and Goddard, M. E. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.
Nelson, D. E., Repetti, P. P., Adams, T. R., Creelman, R. A., Wu, J., Warner, D. C., et al. (2007). Plant nuclear factor Y (NF-Y) B subunits confer drought tolerance and lead to improved corn yields on water-limited acres. Proc. Natl. Acad. Sci. U.S.A. 104, 16450–16455. doi: 10.1073/pnas.0707193104
Nepolean, T., Hossain, F., Arora, K., Sharma, R., Shiriga, K., Mittal, S., et al. (2014). Functional mechanisms of drought tolerance in subtropical maize (Zea mays L.) identified using genome-wide association mapping. BMC Genomics 15:1182. doi: 10.1186/1471-2164-15-1182
Nepolean, T., Hossain, F., Shiriga, K., Mittal, S., Arora, K., Rathore, A., et al. (2013). Unraveling the genetic architecture of subtropical maize (Zea mays L.) lines to assess their utility in breeding programs. BMC Genomics 14:877. doi: 10.1186/1471-2164-14-877
Ng, L.-M., Soon, F.-F., Zhou, X. E., West, G. M., Kovach, A., Suino-Powell, K. M., et al. (2011). Structural basis for basal activity and autoactivation of abscisic acid (ABA) signaling SnRK2 kinases. Proc. Natl. Acad. Sci. U.S.A. 108, 21259–21264. doi: 10.1073/pnas.1118651109
Nikolić, A., Ignjatović-Micić, D., Dodig, D., Andelković, V., and Lazić-Jančić, V. (2012). Identification of QTLs for yield and drought-related traits in maize: assessment of their causal relationships. Biotechnol. Biotechnol. Equip. 26, 2952–2960. doi: 10.5504/bbeq.2012.0016
Ogutu, J. O., Schulz-Streeck, T., and Piepho, H.-P. (2012). Genomic selection using regularized linear regression models: ridge regression, lasso, elastic net and their extensions. BMC Proc. 6:S10. doi: 10.1186/1753-6561-6-S2-S10
Pandey, N., Ranjan, A., Pant, P., Tripathi, R., Ateek, F., Pandey, H., et al. (2013). CAMTA 1 regulates drought responses in Arabidopsis thaliana. BMC Genomics 14:216. doi: 10.1186/1471-2164-14-216
Pedroso, J., Paulo, L., Pires, M., Coelho, R., and Vasconcellos, D. C. (2016). Genomic selection to resistance to Stenocarpella maydis in maize lines using DArTseq markers. BMC Genet. 17, 1–10. doi: 10.1186/s12863-016-0392-3
Pei, Z. M., Murata, Y., Benning, G., Thomine, S., Klüsener, B., Allen, G. J., et al. (2000). Calcium channels activated by hydrogen peroxide mediate abscisic acid signalling in guard cells. Nature 406, 731–734. doi: 10.1038/35021067
Ren, X., Chen, Z., Liu, Y., Zhang, H., Zhang, M., Liu, Q., et al. (2010). ABO3, a WRKY transcription factor, mediates plant responses to abscisic acid and drought tolerance in Arabidopsis. Plant J. 63, 417–429. doi: 10.1111/j.1365-313X.2010.04248.x
Resende, M. F., Muñoz Del Valle, P. R., Acosta, J. J., Resende, M. D., Grattapaglia, D., and Kirst, M. (2011). Stability of Genomic Selection prediction models across ages and environments. BMC Proc. 5:O14. doi: 10.1186/1753-6561-5-S7-O14
Riedelsheimer, C., Technow, F., and Melchinger, A. E. (2012). Comparison of whole-genome prediction models for traits with contrasting genetic architecture in a diversity panel of maize inbred lines. BMC Genomics 13:452. doi: 10.1186/1471-2164-13-452
Riedelsheimer, C., Endelman, J. B., Stange, M., Sorrells, M. E., Jannink, J. L., and Melchinger, A. E. (2013). Genomic predictability of interconnected biparental maize populations. Genetics 194, 493–503. doi: 10.1534/genetics.113.150227
Sabatini, S., Heidstra, R., Wildwater, M., and Scheres, B. (2003). SCARECROW is involved in positioning the stem cell niche in the Arabidopsis root meristem. Genes Dev. 17, 354–358. doi: 10.1101/gad.252503
Seo, J. S., Joo, J., Kim, M. J., Kim, Y. K., Nahm, B. H., Song, S. I., et al. (2011). OsbHLH148, a basic helix-loop-helix protein, interacts with OsJAZ proteins in a jasmonate signaling pathway leading to drought tolerance in rice. Plant J. 65, 907–921. doi: 10.1111/j.1365-313X.2010.04477.x
Seo, P. J., and Park, C.-M. (2009). Auxin homeostasis during lateral root development under drought condition. Plant Signal. Behav. 4, 1002–1004. doi: 10.1104/pp.109.144220.ateral
Shengqiang, Z., Dekkers, J. C. M., Fernando, R. L., and Jannink, J. L. (2009). Factors affecting accuracy from genomic selection in populations derived from multiple inbred lines: a barley case study. Genetics 182, 355–364. doi: 10.1534/genetics.108.098277
Soon, F.-F., Ng, L.-M., Zhou, X. E., West, G. M., Kovach, A., Tan, M. H. E., et al. (2012). Molecular mimicry regulates ABA signaling by SnRK2 kinases and PP2C phosphatases. Science 335, 85–88. doi: 10.1126/science.1215106
Technow, F., Riedelsheimer, C., Schrag, T. A., and Melchinger, A. E. (2012). Genomic prediction of hybrid performance in maize with models incorporating dominance and population specific marker effects. Theor. Appl. Genet. 125, 1181–1194. doi: 10.1007/s00122-012-1905-8
Tuberosa, R., and Salvi, S. (2006). Genomics-based approaches to improve drought tolerance of crops. Trends Plant Sci. 11, 405–412. doi: 10.1016/j.tplants.2006.06.003
Whittaker, J. C., Thompson, R., and Denham, M. C. (2000). Marker-assisted selection using ridge regression. Genet. Res. 75, 249–252. doi: 10.1017/S0016672399004462
VanRaden, P. M., Van Tassell, C. P., Wiggans, G. R., Sonstegard, T. S., Schnabel, R. D., Taylor, J. F., et al. (2009). Invited review: reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 92, 16–24. doi: 10.3168/jds.2008-1514
Wong, C. K., and Bernardo, R. (2008). Genomewide selection in oil palm: Increasing selection gain per unit time and cost with small populations. Theor. Appl. Genet. 116, 815–824. doi: 10.1007/s00122-008-0715-5
Xiong, L., Wang, R. G., Mao, G., and Koczan, J. M. (2006). Identification of drought tolerance determinants by genetic analysis of root response to drought stress and abscisic acid. Plant Physiol. 142, 1065–1074. doi: 10.1104/pp.106.084632
Yoshida, T., Fujita, Y., Sayama, H., Kidokoro, S., Maruyama, K., Mizoi, J., et al. (2010). AREB1, AREB2, and ABF3 are master transcription factors that cooperatively regulate ABRE-dependent ABA signaling involved in drought stress tolerance and require ABA for full activation. Plant J. 61, 672–685. doi: 10.1111/j.1365-313X.2009.04092.x
Zhao, Y., Gowda, M., Liu, W., Würschum, T., Maurer, H. P., Longin, F. H., et al. (2012). Accuracy of genomic selection in European maize elite breeding populations. Theor. Appl. Genet. 124, 769–776. doi: 10.1007/s00122-011-1745-y
Keywords: drought, genomic selection, transcription factor, SNP, parametric, non-parametric, semi-parametric
Citation: Shikha M, Kanika A, Rao AR, Mallikarjuna MG, Gupta HS and Nepolean T (2017) Genomic Selection for Drought Tolerance Using Genome-Wide SNPs in Maize. Front. Plant Sci. 8:550. doi: 10.3389/fpls.2017.00550
Received: 17 February 2017; Accepted: 27 March 2017;
Published: 21 April 2017.
Edited by:
Prashant Vikram, International Maize and Wheat Improvement Center, MexicoReviewed by:
Jiafa Chen, Henan Agricultural University, ChinaDeepmala Sehgal, International Maize and Wheat Improvement Center, Mexico
Copyright © 2017 Shikha, Kanika, Rao, Mallikarjuna, Gupta and Nepolean. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thirunavukkarasu Nepolean, dG5lcG9sZWFuQGdtYWlsLmNvbQ==; dG5lcG9sZWFuQHlhaG9vLmNvbQ==
 Mittal Shikha
Mittal Shikha Arora Kanika1
Arora Kanika1 Atmakuri Ramakrishna Rao
Atmakuri Ramakrishna Rao Mallana Gowdra Mallikarjuna
Mallana Gowdra Mallikarjuna Thirunavukkarasu Nepolean
Thirunavukkarasu Nepolean