- 1Key Laboratory of Tropical Forest Ecology, Xishuangbanna Tropical Botanical Garden, Chinese Academy of Sciences, Mengla, China
- 2Forest Ecology and Forest Management Group, Department of Forestry, Wageningen University, Wageningen, Netherlands
- 3Key Laboratory of Economic Plants and Biotechnology, Kunming Institute of Botany, Chinese Academy of Sciences, Kunming, China
- 4Key Laboratory of Forest Ecology and Management, Institute of Applied Ecology, Chinese Academy of Sciences, Shenyang, China
Leaf–stem allometry is an important spectrum that linked to biomass allocation and life history strategy in plants, although the determinants and evolutionary significance of leaf–stem allometry remain poorly understood. Leaf and stem architectures – including stem area/mass, petiole area/mass, lamina area/mass, leaf number, specific leaf area (LA), and mass-based leafing intensity (LI) – were measured on the current-year branches for 28 Ficus species growing in a common garden in SW China. The leaf anatomical traits, stem wood density (WD), and stem anatomical and mechanical properties of these species were also measured. We analyzed leaf–stem allometric relationships and their associations with stem hydraulic ad mechanical properties using species-level data and phylogenetically independent contrasts. We found isometric relationship between leaf lamina area/mass and stem area/mass, suggesting that the biomass allocation to leaf was independent to stem size. However, allometric relationship between LA/mass and petiole mass was found, indicating large leaves invest a higher fractional of biomass in petiole than small ones. LI, i.e., leaf numbers per unit of stem mass, was negatively related with leaf and stem size. Species with larger terminal branches tend to have larger vessels and theoretical hydraulic conductivity, but lower WD and mechanical strength. The size of leaf lamina, petiole, and stem was correlated positively with stem theoretical hydraulic conductivity, but negatively with stem WD and mechanical strength. Our results suggest that leaf–stem allometry in Ficus species was shaped by the trade-off between stem hydraulic efficiency and mechanical stability, supporting a functional interpretation of the relationship between leaf and stem dimensions.
Introduction
Leaf surface area spans six orders of magnitude across terrestrial plants species (Milla and Reich, 2007; Díaz et al., 2016), and the functional and evolutionary significance of this diverse feature is a subject of strong interest (Ackerly and Reich, 1999). Leaves intercept light and acquire carbon, while stems transport water with nutrients and mechanically support the leaves, thus leaf and stem traits are expected to be highly coordinated biomechanically and physiologically (Westoby et al., 2002). At twig level, traits such as twig size, wood density (WD), or internode length have been reported to account for cross-species variation in leaf size (Westoby and Wright, 2003; Poorter and Rozendaal, 2008). Corner (1949) identified two basic properties of plant architecture: larger leaves are borne on thicker stems, and plants with thicker stems branch more sparsely, and vice versa.
This “Corner’s rules” has been tested empirically within and across species and environments (White, 1983a,b; Ackerly and Donoghue, 1998; Brouat et al., 1998; Olson et al., 2009). Positive allometric relationships between twig and leaf size are often found across species in different vegetation types (Westoby and Wright, 2003; Preston and Ackerly, 2003; Sun et al., 2006; Yang et al., 2010) and taxonomic groups (White, 1983a,b; Ackerly and Donoghue, 1998; Brouat et al., 1998; Normand et al., 2008), which implies that larger leaves need disproportionally more in supporting and transporting structures than smaller ones (Niinemets et al., 2006). However, isometric relationships have also been observed between twig and leaf size (e.g., Brouat et al., 1998; Li et al., 2008; Zhang et al., 2016). Therefore, the exact nature of this relationship and why it should occur are far from conclusive and the mechanism underlying Corner’s rules needs further investigations (Olson et al., 2009).
The leaf–stem size spectrums are often expected partly as a result of the mechanical and conductive demands of leaves (Niklas, 1994; Enquist, 2002), i.e., larger leaves would require a larger cross-sectional area for water supply and greater mechanical support (Shinozaki et al., 1964). Normand et al. (2008) suggested the leaf–stem allometry in mango cultivars is linked to the trade-off between hydraulic efficiency and mechanical strength of wood, supporting a functional interpretation leaf–stem size spectrum. However, it is not so obvious why stem cross-sectional area should scale positively with mean leaf size (Smith et al., 2017).
Plant xylem plays three main functions, i.e., mechanical support, water conduction, and water and photosynthate storage (Bittencourt et al., 2016). Vessel-bearing angiosperms allocated limited xylem space and resources for building different structures that acting different function, i.e., vessels transport water, fibers provide mechanical support, and parenchyma cells function for storage (Baas et al., 2004). The conflicting structural requirements in xylem design would lead a “trade-off triangle” among mechanical strength, conductive efficiency, and resistance to embolism (Sperry et al., 2008; Brodersen, 2016). An increase of leaf surface area requires the increases of stem conductive area or efficiency for water supply, and meanwhile increases of strength for mechanical loads. However, these conflicting demands cannot be accomplished unless plants adjust their xylem structure designs. It is still unclear that how xylem hydraulic and mechanical properties varied with stem/leaf dimensions, and if these changes could shape the stem–leaf size relationships.
In the study, we measured leaf, stem, and petiole dimensions (area, mass, and anatomical and mechanical properties) of terminal branches of 28 Ficus species growing in a common garden in tropical China. We analyzed the allometric relationships among these traits, both across species and across phylogenetically independent contrasts (PICs). We asked the questions: (1) are the scaling relationships between leaf size and stem/petiole size isometry or allometry? (2) Can the adjustments of plant xylem structures along with leaf/stem dimensions explain scaling relationships between leaves and stem size. We tested the specific hypothesis that there is a trade-off between hydraulic and mechanical function of stems, and this trade-off has compensated effect on the twig–leaf size allometric relationship.
Materials and Methods
Study Site and Species
This study was conducted at Xishuangbanna Tropical Botanical Garden (XTBG, 21°41′ N, 101°25′ E, and altitude 570 m), Yunnan, Southwest China. The region is dominated by warm, wet air masses from the Indian Ocean in summer and continental air masses from temperate regions in winter. The mean annual temperature is 21.7°C, with the monthly mean temperature being 15.9°C during the coldest month (December) and 25.7°C during the warmest month (June). The annual rainfall is 1560 mm, with more than 80% occurring during the wet season from May to October.
We selected 28 tree species all belong to Ficus genus that commonly found in the rainforests of Xishuangbanna (Supplementary Table S1). All plants were grown in a common garden of XTBG with relatively open habitats and homogeneous soil, and have reachable from the ground or by using a ladder. We sampled three-to-five branches randomly from three individuals per species. All the branches were located at the outer surface of the plant’s crown. A total 250 branches were sampled from the 28 Ficus species. Samples were taken from May to September of 2010 and 2011, when seasonal shoot growth and leaf expansion have been completed.
Twig Architecture
For each sampled branch, a current-year terminal (un-branched) shoot (here defined as “twig”) with no herbivore damage was selected for trait measurements. For each twig sample, leaf lamina, petiole, and stem were separated. Leaf numbers were counted and leaf area (LA) was measured with an area meter (Li-Cor 3000A; Lincoln, NE, United States). Stem and petiole diameters were measured with a vernier caliper. Twig stem, all leaf laminas, and petioles from a twig were oven dried at 70°C to constant weight, and their dry masses were weighted. Specific leaf area (SLA) was expressed as LA per unit of dry mass (m2 kg-1). The individual lamina area (mass) was calculated as the total area (mass) divided by leaf number. Individual petiole mass was calculated as the total petiole mass divided by leaf number. Leafing intensity (LI), a common developmental correlate of leaf size, was defined as leaf numbers per unit of stem mass (no. g-1).
Stem Anatomical and Biomechanical Properties
After removing the bark and pith with a razor blade, the fresh wood (FW) are weighted and wood fresh volume was measured the water displacement method. Wood saturated weight (SW) was determined after submerging under water for 48 h for rehydration. Wood samples were then over-dried for at least 48 h at 70°C to determine the dry weight (DW). Stem saturated water content (SWC) was calculated as: SWC = (FW - DW)/(SW – DW) × 100%. WD (g cm-3) was determined by dividing the dry mass by the volume of the samples.
We made transvers wood cross-sections with a microtome, stained the sections with safranin. We photographed sections with a digital camera mounted on microscope (Leica DM2500, Germany). We used ImageJ software1 to measure vessel major and minor diameter, as well as vessel density (VD). Since vessel is mostly elliptical, vessel diameter was calculated as D = [32(ab)3/(a2+b2)]1/4, where a and b are the major and minor axis dimensions, respectively (Lewis, 1992). Hydraulic weighted vessel diameter (Dh) is calculated as Dh = [1/nΣD4]1/4. VD (no. mm-2) was calculated as number of vessels per unit of xylem area (mm-2). We calculated vessel fraction (VF) as the product of vessel area and VD. The theoretical specific hydraulic conductivity (Ktheo, kg m-1 MPa-1 s-1, a measure of xylem porosity) was estimated according to the Hagen–Poiseuille equation: Ktheo = μρ/(128μAs)[ΣD4], where ρ is the density of water (998.2 kg m-3 at 20°C), μ is the viscosity of water (1.002 × 10-9 MPa s-1 at 20°C), and As is the cross-sectional area of sapwood (Tyree and Zimmermann, 2002). The calculated Ktheo is substantially higher than actual conductivity as it ignores resistance of water flowing through the vessel walls. However, calculated Ktheo appears to be a good proxy for conductivity because vessel walls contribute a relatively constant 56% to total resistance in conduits (Sperry et al., 2006).
The modulus of elasticity (MOE) of stem (Young’s modulus, MPa) was measured by three-point bending method with an INSTRON mechanical testing machine with a 5 kN load cell (INSTRON Corporation, Canton, MA, United States). Stem segments had length-to-diameter ratios of 25:1 to avoid share. Stem segments were placed on a steel frame apparatus at two supporting points at a precise span distance. Consecutive weights were added to a pannier suspended from the exact center of the stem segment. Flexural stiffness (EI) and structural Young’s modulus (MOE) were calculated from linear relationships resulting from observed deflections of stem segments after adding a sequence of weights.
Leaf Anatomy
For each sampled branch, three to five full-developed leaves were sampled from twigs closed to those used for measuring twigs architecture. Hand transverse sections were made for leaves and then mounted on glass slides, and then these sections were examined and photographed at 10× magnifications with a light microscope (Leica DM2500, Germany). Total leaf thickness (LT), thickness of the upper epidermis (UET, mm), lower epidermis (LET, mm), palisade tissue (PT, mm), and spongy tissue (SP, mm) were measured with ImageJ software. Stomatal size (SS) was represented as the guard cell length and stomatal density (SD) was calculated as the number per unit LA.
Statistical Analysis and Comparative Methods
Results from hierarchical ANOVA revealed that trait variations among species consistently the largest, i.e., explained 78.6–98.8%. Trait variations among individuals from the same species, and among twigs from the same individual, were mostly less than 20% (Supplementary Table S2). For interspecific comparisons, trait values were averaged arithmetically per individual and then per species. The species mean trait values were log10-transformed to fit the normal distribution (Kerkhoff and Enquist, 2009).
The relationships among paired traits were described by a mathematical equation of the type y = γ xβ, where y and x are variables or parameters.[AQ]edit They can be linearized through a logarithm transformation of both variables: Y = α + βX, where Y = log(y), α = log(γ), and X = log(x). The linear relationship is described by its slope β or scaling coefficient and its y-intercept α or allometric constant. The value of the slope determines the relationship is isometric (β = 1) or allometric (β ≠ 1). Standardized major axis (SMA) regression was used to estimate the parameters of the allometric equation, by using the R package “SMATR” (Warton et al., 2006).
We assessed relationships between traits using Pearson correlation for 24 traits of all the 28 Ficus species. We carried out a multiple factor analysis (MFA) for the measured stem and leaf traits, with the method of Escofier and Pages (1994). We performed the MFA for 13 leaf and 11 stem/petiole trait means of the 28 Ficus species, by using the FactoMineR package (Lê et al., 2008) in R v.3.23 (R Development Core Team, 2004).
To test if correlations resulted from phylogeny relatedness, we also calculated pairwise correlations using PICs (Felsenstein, 1985; Garland et al., 1992). PICs for the 24 functional traits were calculated based on a phylogeny tree of the 28 Ficus species, using the “ape” package (Felsenstein, 1985; Garland et al., 1992). The phylogenetic relationships among the 28 Ficus species were inferred from nuclear ITS and G3pdh sequences deposited in GenBank (Supplementary Table S1; Xu et al., 2011). Sequences alignment was performed using Clustal W default settings followed by a manual adjustment in the MEGA 5.2 software (Tamura et al., 2007). Phylogenetic tree was estimated using Bayesian methods with the MrBayes v. 3.2 (Supplementary Figure S1).
Results
The total and individual LA (mass) scaled positively with stem area (mass), with best-fit common regression slopes were not significantly different with slope 1.0 (Figures 1A,D and Table 2). Petiole area (mass) was highly related to lamina area (mass), with the scaling slopes between petiole and leaf mass were significantly smaller than 1.0, indicating an allometric scaling relationship between petiole and leaf lamina (Figures 1B,E and Table 2). Leaf size showed a negative, isometric relationship with mass-based LI, with the best-fit common regression slopes ranged from -0.9 to -1.1 (Figure 1D). A significant positive allometric relationship was found between lamina mass and lamina area, with common slopes (1.1–1.6) significantly departed from the value of 1.0 (Table 2 and Supplementary Figure S2).
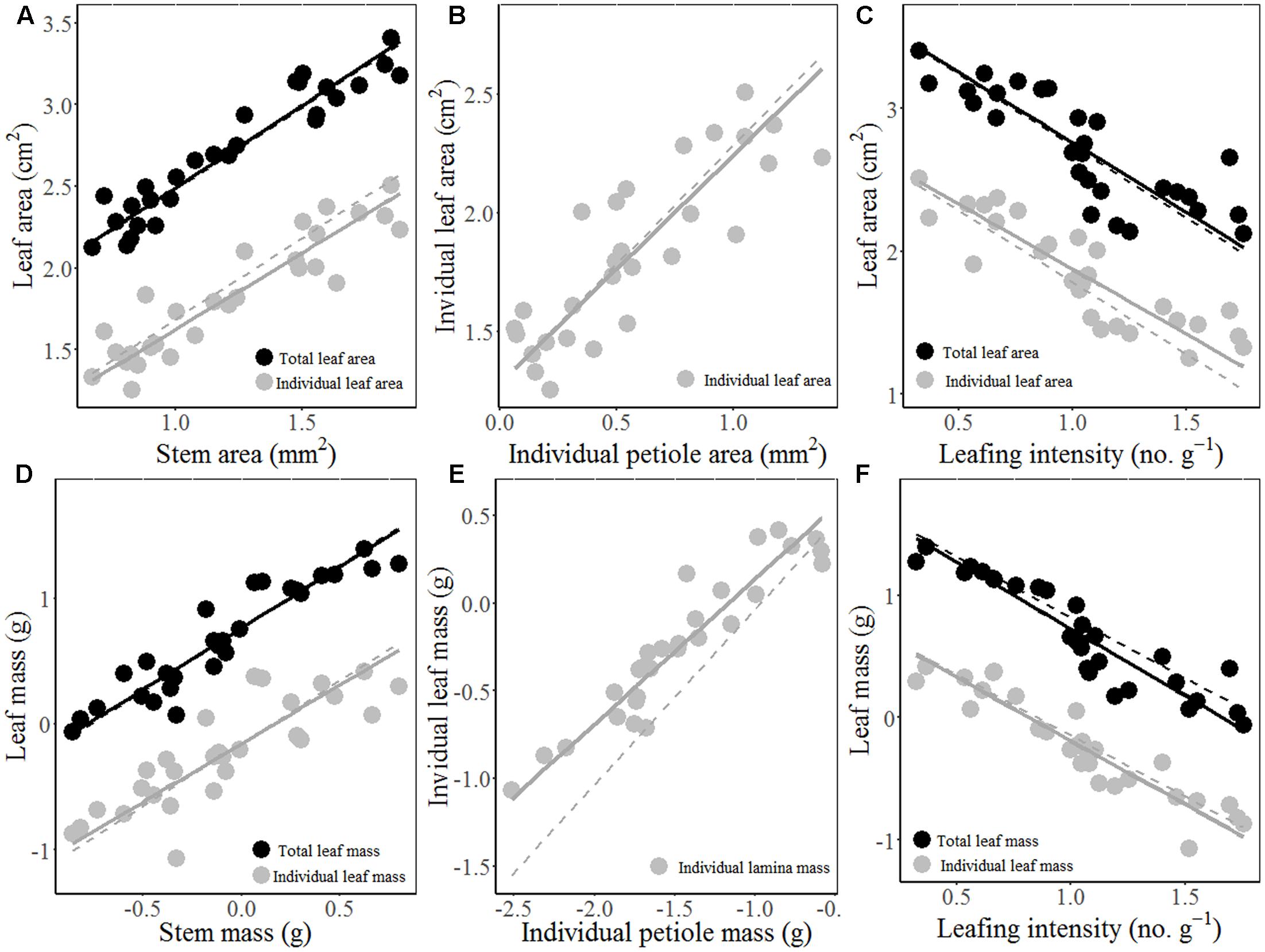
FIGURE 1. The scaling relationships between stem area and LA/mass (A,D); individual petiole area/mass and lamina area/mass (B,E), and mass-based LI and LA/mass (C,F) for 28 Ficus tree species. The solid lines are the standardized major axis (SMA) regression curves. The dashed lines are the slopes equal to 1.0 or –1.0.
The results of MFA revealed three trade-offs (Figure 2): i.e., (1) trade-off between stem hydraulic efficiency and mechanical strength; (2) trade-off between SLA and the thickness of all lamina tissues, (3) trade-off between leaf/stem size and LI. The first axis of MFA accounted for 44.79% of the total variance among the 24 traits, which loaded mainly the leaf architecture traits, i.e., stem area/mass, LA/mass, petiole area/mass, and mass-based LI (Figure 2). In other word, species with larger leaves have thicker stem and petiole, but lower mass-based LI. Meanwhile, the first axis also loaded positively the traits associated with stem hydraulic efficiency (i.e., Dh, VF, Ktheo, and SWC), but loaded negatively the traits linked to stem mechanical strength (WD and MOE). The second axis accounted for 24.85% of the variance, and mainly loaded SLA and traits related to lamina tissue thickness (LT, UET, PT, SP, and LET) and SS and SD (Figure 2 and Supplementary Figure S3). The results of the MFA based on PICs were generally consistent with that of cross-species means (Supplementary Figure S4 and Table S3).
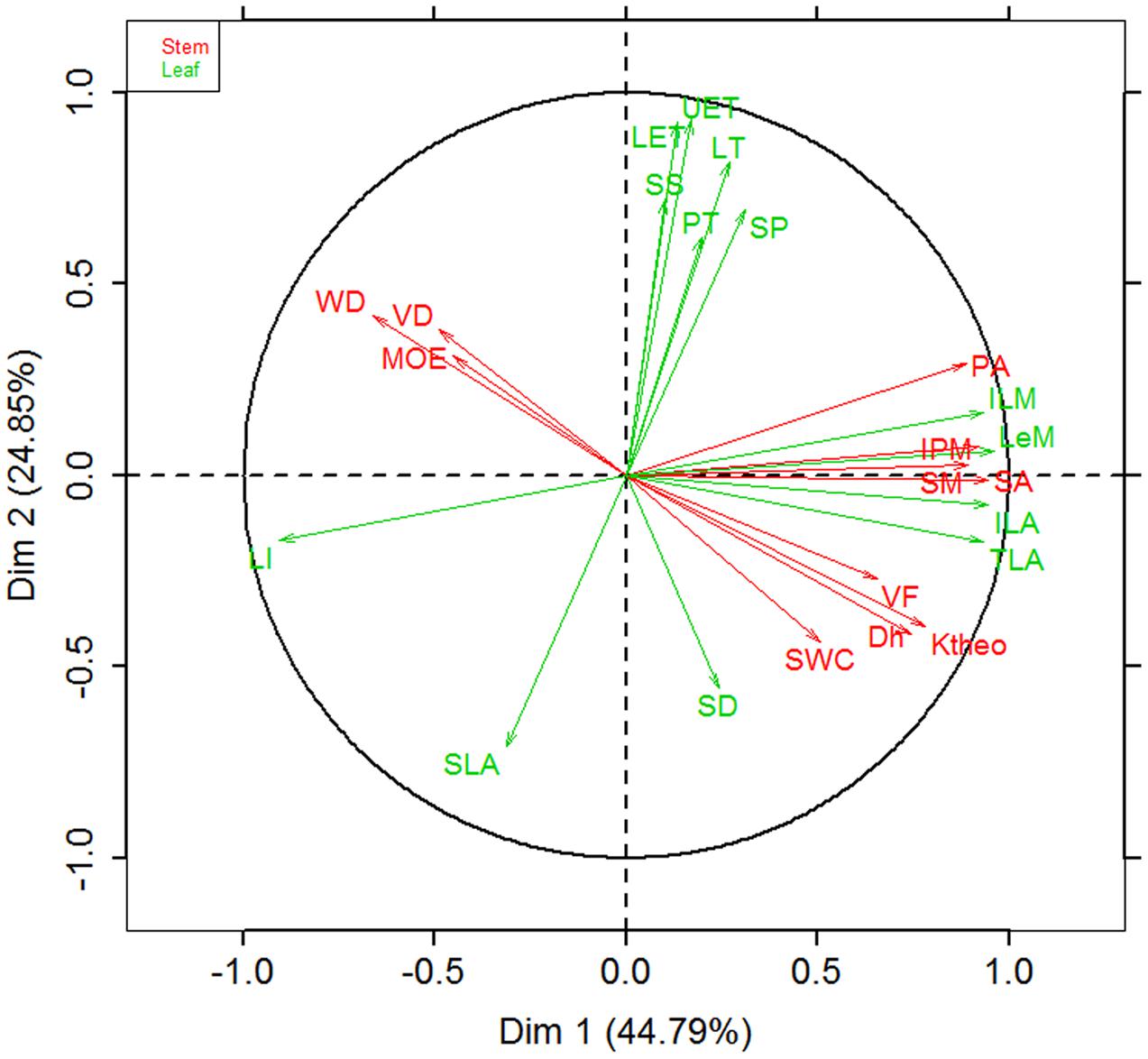
FIGURE 2. Biplot of trait relationships based on multiple factor analysis (MFA) on cross-species means of 11 stem/petiole (red) and 13 leaf traits (green) of 28 Ficus species. Trait abbreviations and unit of measure are shown in Table 1. Values in parentheses in the axis labels are percentages of variance explained.
Figure 3 showed the trade-offs between stem hydraulic efficiency and mechanical strength. Species with larger xylem vessel size (Dh) had lower VD, but higher VF and thus high theoretical hydraulic conductivity (Ktheo) (Figures 3A–C). On the other hand, theoretical hydraulic conductivity (Ktheo) showed negative correlations with WD and MOE (Figures 3D–F). Thus, higher xylem hydraulic efficiency can only be achieved by the cost of reduced WD and mechanical strength. As compared with cross-species correlations, the correlations based on PICs were generally weaker, and in some case became non-significant (i.e., vessel diameter vs. fraction and Ktheo vs. MOE).
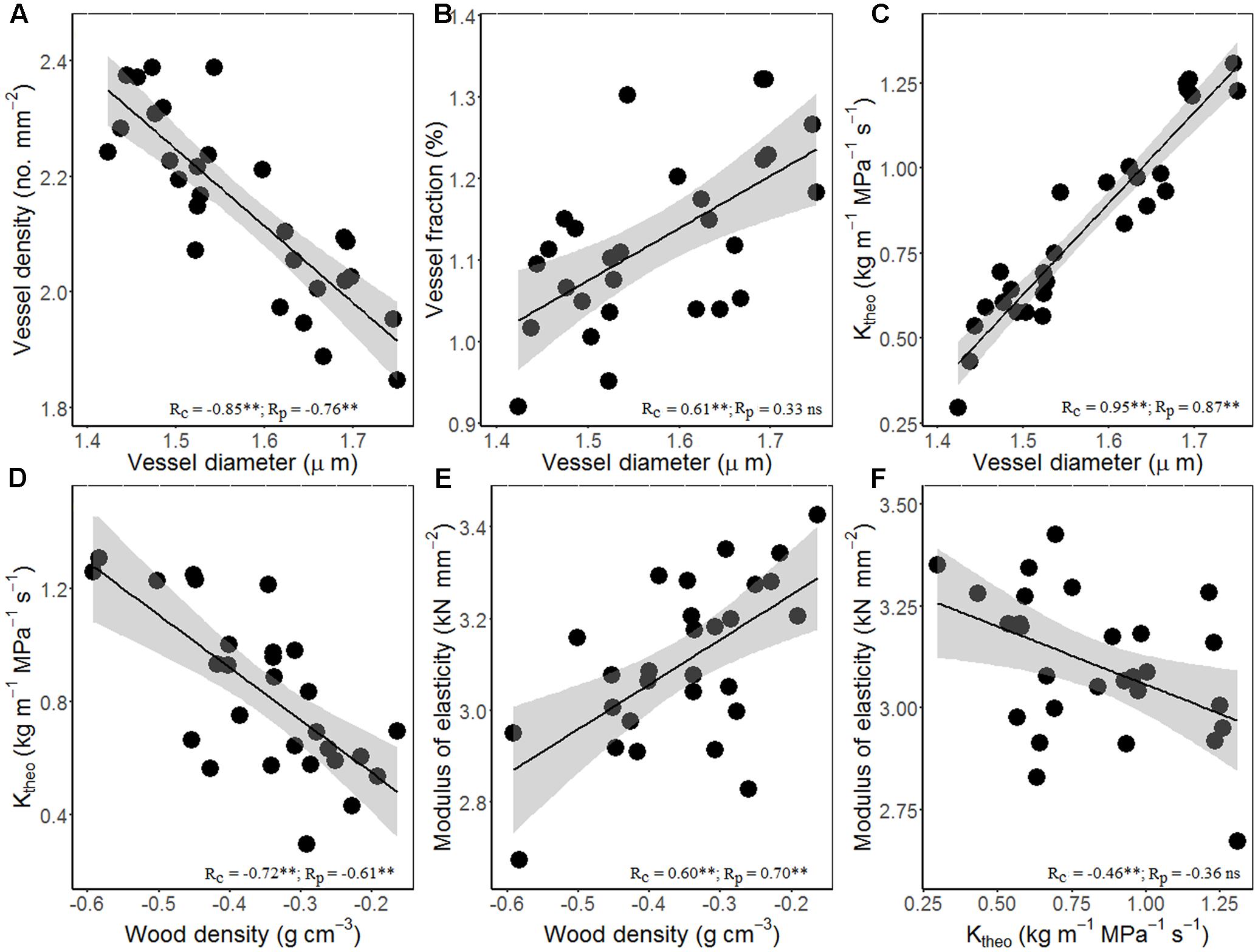
FIGURE 3. Relationships among stem hydraulic architectural traits, wood density (WD), and mechanical properties for 28 Ficus species. (A) Vessel diameter vs. density, (B) vessel diameter vs. fraction, (C) vessel diameter vs. theoretical hydraulic conductivity (Ktheo), (D) WD vs. Ktheo, (E) WD vs. modulus of elasticity (MOE), and (F) Ktheo vs. MOE. Note the log10 scales in panels. Shading areas represent 95% confidence intervals of linear regression. Pearson’s cross-species (Rc) and phylogenetically independent contrast (PIC) (Rp) correlation coefficients are shown. ns, p > 0.05; ∗p < 0.05; ∗∗p < 0.01.
Interestingly, wood hydraulic and mechanical traits varied with stem size of terminal branches (Figure 4). For example, stem area correlated positively with vessel lumen diameter (Dh), VF, and theoretical hydraulic conductivity (Ktheo), but negatively with VD, WD, and MOE. In other word, thicker stem is more efficient for water transport, but less efficient for mechanical stability. Moreover, significant positive correlations were found between stem theoretical hydraulic conductivity (Ktheo) and petiole area/mass and LA/mass for both cross-species means and PICs (Figure 5). However, stem WD was negatively correlated with stem, petiole, and leaf dimensions (Figures 4, 5).
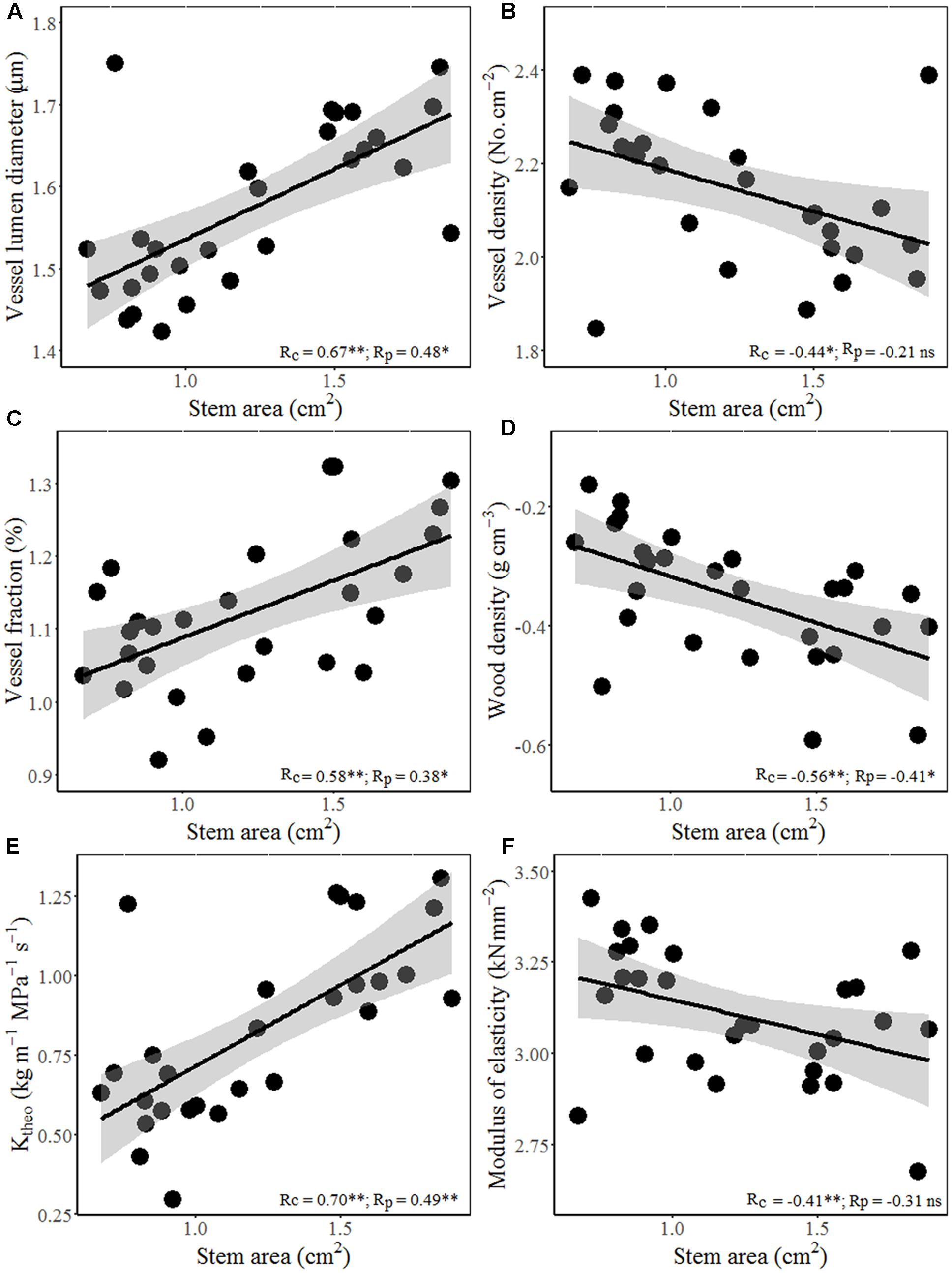
FIGURE 4. Relationships between stem area and hydraulic architecture and mechanical traits for 28 Ficus species. Stem area with (A) vessel diameter, (B) vessel density (VD), (C) vessel fraction (VF), (D) WD, (E) theoretical hydraulic conductivity (Ktheo), and (F) MOE. Note the log10 scales in panels. Shading areas represent 95% confidence intervals of linear regression. Pearson’s cross-species (Rc) and PIC (Rp) correlation coefficients are shown. ns, p > 0.05; ∗p < 0.05; ∗∗p < 0.01.
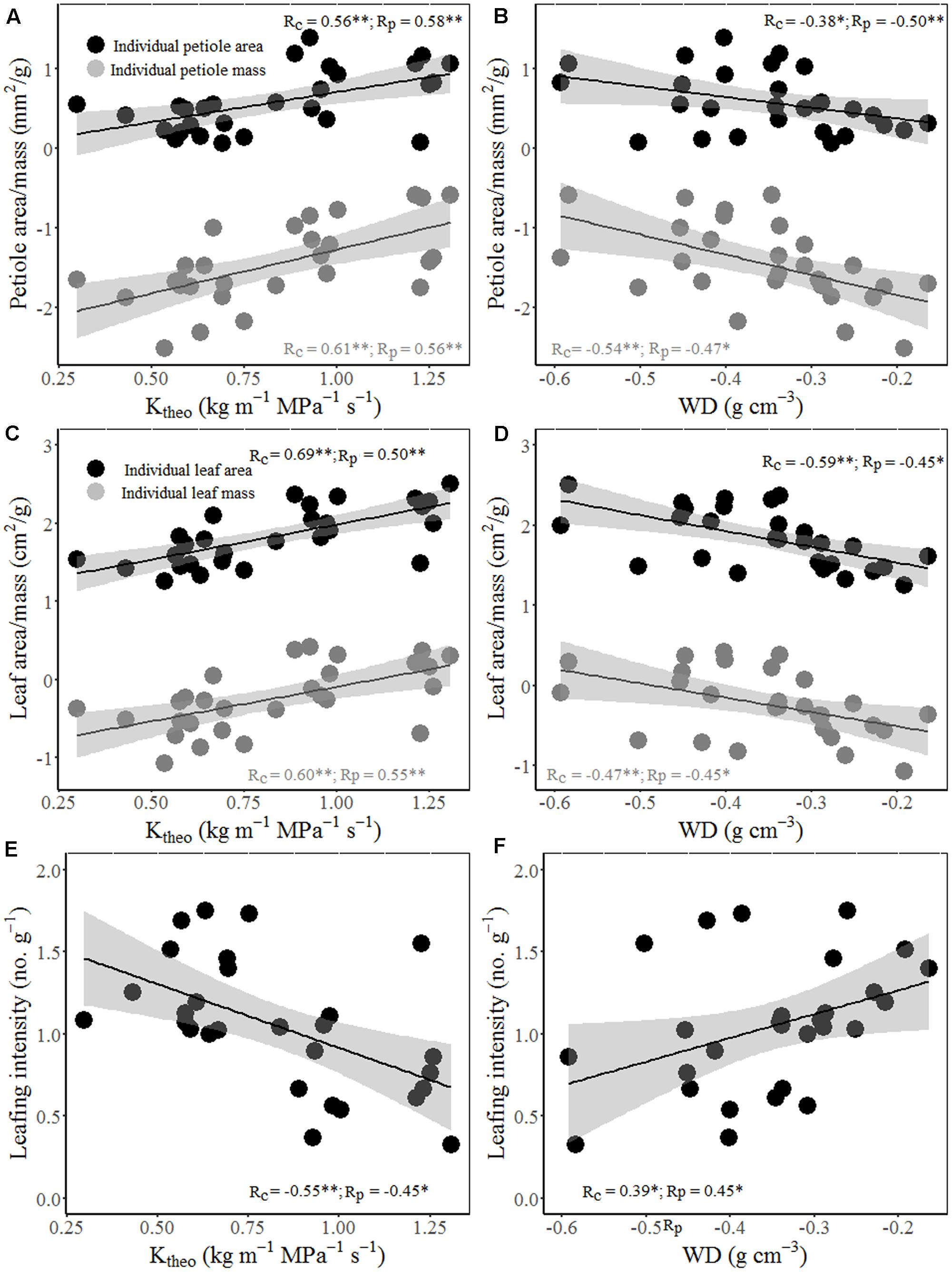
FIGURE 5. Relationships between theoretical hydraulic conductivity (Ktheo) and petiole area/mass (A), LA/mass (C) and mass-based LI (E); and between WD and petiole area/mass (B), LA/mass (D) and mass-based LI (F). Note the log10 scales in panels. Shading areas represent 95% confidence intervals of linear regression. Pearson’s cross-species (Rc) and PIC (Rp) correlation coefficients are shown. ∗p < 0.05; ∗∗p < 0.01.
Discussion
We found an isometric relationship between leaf size and stem size, indicating that the increase of total or individual LA/mass is generally proportional to the increase of stem area/mass (Figures 1A,D and Table 2). These results are consistent with the findings of Brouat et al. (1998) and Li et al. (2008), but in contrast to the others (Preston and Ackerly, 2003; Westoby and Wright, 2003; Sun et al., 2006; Yang et al., 2010). However, the allometrical relationships between lamina size and petiole size (Figures 1B,E and Table 1) implied that more biomass investment to petiole with a unit increase of lamina size.
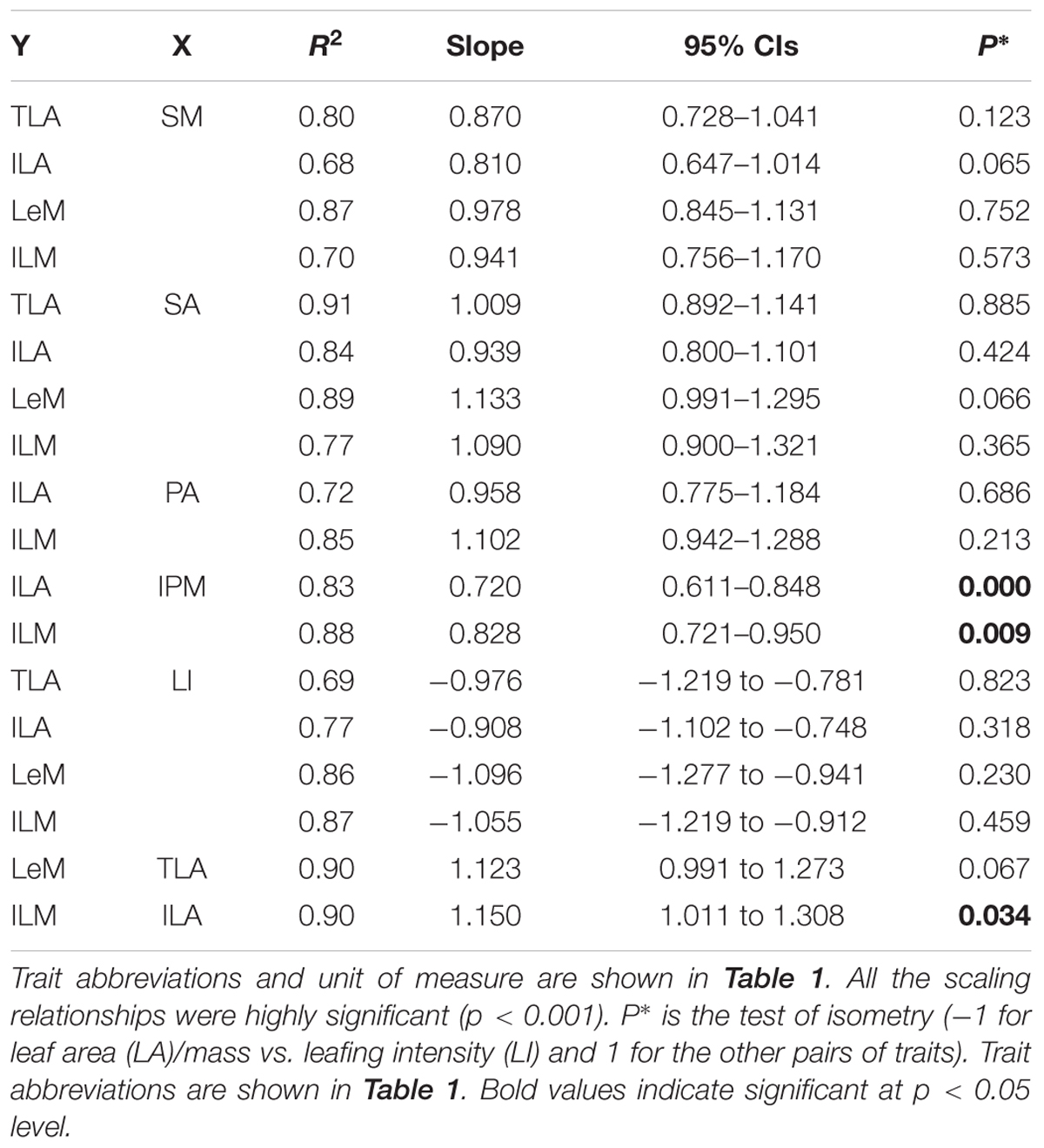
TABLE 2. Standardized major axis regression slopes and 95% confidence intervals (CIs) of the slopes of log–log linear relationships among traits of 28 Ficus tree species.
Leaf size scaled negatively and isometrically with LI (number of leaves per unit of stem mass) (Figures 1C,E), which demonstrates the generality of the leaf size/number trade-off as found by other studies (Yang et al., 2008; Xiang et al., 2010; Yan et al., 2012). Kleiman and Aarssen (2007) first reported the isometric trade-off for 24 woody species; however, other studies have demonstrated that the scaling relationship between leaf size and LI can be either isometric (Li et al., 2008; Ogawa, 2008; Yang et al., 2008; Milla, 2009) or allometric (Yang et al., 2008; Milla, 2009). Lamina area was positive correlated (allometrically) with lamina mass (slope = 1.15, Supplementary Figure S2), which implied that larger leaves have greater mass per unit LA than smaller leaves, thus a greater cost for building and maintaining a unit of LA (Milla and Reich, 2007; Niklas et al., 2007; Li et al., 2008).
Although more vessels can transport more water, calculated stem theoretical hydraulic conductivity (Ktheo) is largely determined by vessel diameter (Dh), because Ktheo increases linearly with VD but with the forth power of Dh, and because of the tight negative relationship between Dh and VD (Figure 3). Significant negative correlation between Ktheo and WD and MOE suggests a trade-off between water transport and mechanical support. Wood composed of closely spaced large vessels will have low density with high hydraulic conductivity, whereas wood composed of small vessels spaced widely within a fiber matrix will be dense with low hydraulic conductivity (Preston et al., 2006; Zanne et al., 2010).
Total LA supported by a twig should be proportional to the xylem conductive area, as predicted by the “pipe model” (Shinozaki et al., 1964). Interestingly, species with bigger size of terminal stems have larger vessels and higher proportion of vessel area in xylem (higher VF), thus higher theoretical hydraulic conductivity (Figures 4A–C). These results indicated that higher conductive and lower density woody species grow more rapidly, not only in volume, but also in stem and total leaf mass. Species with higher hydraulic efficiency, expressed by larger Dh, VF, and Ktheo, should be able to transport more water and thus deploy a larger total LA per stem (Cavender-Bares et al., 2004). This is also confirmed by a positive correlation between stem hydraulic efficiency and leaf and petiole size (Figures 5A–D). Moreover, higher theoretical hydraulic conductivity and lower WD were associated with lower LI (leaf numbers per sapwood mass) (Figures 5E,F), which implied that few larger leaves gave a better return for investment on the stem than many smaller leaves (Smith et al., 2017).
In addition to supplying leaves with water and nutrients, twigs also provide mechanical support for static loads and the drag forces exerted on leaves by winds (Niklas and Enquist, 2002). However, species with larger terminal branches tend to have lower WD and mechanical strength (MOE) (Figures 4D–F), indicating that bigger branches are less efficient for mechanical strength. The negative relations between leaf size and stem mechanical properties invoke an indirect correlation via plant hydraulics, i.e., species with lower WD have higher hydraulic conductivity per sapwood area as a result of having a higher proportion of stem cross-section taken up by vessel lumen (Martínez-Cabrera et al., 2009), which in turn allow larger LA to be deployed per stem (Wright et al., 2006). For the biomechanical reasons, the relationship between lamina size and petiole mass is allometric rather than isometric (Figure 1; Li et al., 2008).
Conclusion
We provide evidence that leaf–stem size follows an isometric relationship across 28 Ficus species growing in a common garden of tropical China. However, large leaves tend to have a larger fractional biomass investment in petioles. Larger stems have wider vessel lumens in the xylem and achieve higher stem specific hydraulic conductivity, but the function of mechanical strength is diminished with less dense wood. The trade-off between hydraulic efficiency and mechanical strength in xylem may shape the leaf–stem allometric relationships. We provide functional interpretation of the relationships between leaves and stem dimensions.
Author Contributions
Z-XF and P-LF carried out the experiment and collected the data. Z-XF and FS analyzed the data and wrote the first draft of the manuscript. FS, S-BZ, and G-YH contributed to data analysis, writing, and interpretation. All authors contributed critically to the drafts and approved the final version of the manuscript.
Funding
This work was financially funded by the National Natural Science Foundation of China (Nos. 31770533, 31370496, 91230202) and the Outstanding Young Scientists Program of Chinese Academy of Sciences (2011278).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Dr. Jian-Li Zhao for his help on constructing phylogeny tree. We thank Hong Ma, Qiuyun Yang, Hui Jiang, and Shimei Ji for their assistance in sampling and wood and leaf anatomical work.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fpls.2017.01619/full#supplementary-material
Footnotes
References
Ackerly, D. D., and Donoghue, M. J. (1998). Leaf size, sapling allometry, and Corner’s rules: phylogeny and correlated evolution in Maples (Acer). Am. Nat. 152, 767–791. doi: 10.1086/286208
Ackerly, D. D., and Reich, P. B. (1999). Convergence and correlation among leaf size and function in seed plants: a comparative test using independent contrasts. Am. J. Bot. 86, 1272–1281. doi: 10.2307/2656775
Baas, P., Ewers, F. W., Davis, S. D., and Wheeler, E. A. (2004). “Evolution of xylem physiology,” in The Evolution of Plant Physiology, eds A. R. Hemsley and I. Poole (London: Elsevier Academic Press), 273–295. doi: 10.1016/B978-012339552-8/50016-0
Bittencourt, P. R. L., Pereira, L., and Oliveira, R. S. (2016). On xylem hydraulic efficiencies, wood space-use and the safety-efficiency tradeoff. New Phytol. 211, 1152–1155. doi: 10.1111/nph.14044
Brodersen, C. R. (2016). Finding support for theoretical tradeoffs in xylem structure and function. New Phytol. 209, 8–10. doi: 10.1111/nph.13763
Brouat, C., Gibernau, M., Amsellem, L., and McKey, D. (1998). Corner’s rules revisited: ontogenetic and interspecific patterns in leaf-stem allometry. New Phytol. 139, 459–470. doi: 10.1046/j.1469-8137.1998.00209.x
Cavender-Bares, J., Kitajima, K., and Bazzaz, F. A. (2004). Multiple trait associations in relation to habitat differentiation among 17 Floridian oak species. Ecol. Monogr. 74, 635–662. doi: 10.1890/03-4007
Corner, E. H. (1949). The durian theory or the origin of the modern tree. Ann. Bot. 13, 367–414. doi: 10.1093/oxfordjournals.aob.a083225
Díaz, S., Kattge, J., Cornelissen, J. H., Wright, I. J., Lavorel, S., Dray, S., et al. (2016). The global spectrum of plant form and function. Nature 529, 167–171. doi: 10.1038/nature16489
Enquist, B. J. (2002). Universal scaling in tree and vascular plant allometry: toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 22, 1045–1064. doi: 10.1093/treephys/22.15-16.1045
Escofier, B., and Pages, J. (1994). Multiple factor analysis (AFMULT package). Comput. Stat. Data Anal. 18, 121–140. doi: 10.1016/0167-9473(94)90135-X
Felsenstein, J. (1985). Phylogenies and the comparative method. Am. Nat. 125, 1–15. doi: 10.1086/284325
Garland, T. J., Harvey, P. H., and Ives, A. R. (1992). Procedures for the analysis of comparative data using phylogenetically independent contrasts. Syst. Biol. 41, 18–32. doi: 10.1093/sysbio/41.1.18
Kerkhoff, A. J., and Enquist, B. J. (2009). Multiplicative by nature: why logarithmic transformation is necessary in allometry. J. Theor. Biol. 257, 519–521. doi: 10.1016/j.jtbi.2008.12.026
Kleiman, D., and Aarssen, L. W. (2007). The leaf size/number trade-off in trees. J. Ecol. 95, 376–382. doi: 10.1111/j.1365-2745.2006.01205.x
Lê, S., Josse, J., and Husson, F. (2008). FactoMineR: an R package for multivariate analysis. J. Stat. Softw. 25, 1–18. doi: 10.18637/jss.v025.i01
Lewis, A. M. (1992). Measuring the hydraulic diameter of a pore or conduit. Am. J. Bot. 79, 1158–1161. doi: 10.2307/2445215
Li, G. Y., Yang, D. M., and Sun, S. C. (2008). Allometric relationships between lamina area, lamina mass and petiole mass of 93 temperate woody species vary with leaf habit, leaf form and altitude. Funct. Ecol. 22, 557–564. doi: 10.1111/j.1365-2435.2008.01407.x
Martínez-Cabrera, H. I., Jones, C. S., Espino, S., and Schenk, H. J. (2009). Wood anatomy and wood density in shrubs: responses to varying aridity among transcontinental transects. Am. J. Bot. 96, 1388–1398. doi: 10.3732/ajb.0800237
Milla, R. (2009). The leafing intensity premium hypothesis tested across clades, growth forms and altitudes. J. Ecol. 97, 972–983. doi: 10.1111/j.1365-2745.2009.01524.x
Milla, R., and Reich, P. B. (2007). The scaling of leaf area and mass: the cost of light interception increases with leaf size. Proc. Biol. Sci. 274, 2109–2114. doi: 10.1098/rspb.2007.0417
Niinemets,Ü., Portsmuch, A., and Tobias, M. (2006). Leaf size modifies support biomass distribution among stems, petioles and mid-ribs in temperate plants. New Phytol. 171, 91–104. doi: 10.1111/j.1469-8137.2006.01741.x
Niklas, K. J. (1994). Plant Allometry: the Scaling of Form and Process. Chicago, IL: University of Chicago Press.
Niklas, K. J., Cobb, E. D., Niinemet,Ü., Reich, P. B., Sellin, A., Shipley, B., et al. (2007). “Diminishing returns” in the scaling of functional leaf traits across and within species groups. Proc. Natl. Acad. Sci. U.S.A. 104, 8891–8896. doi: 10.1073/pnas.0701135104
Niklas, K. J., and Enquist, B. J. (2002). Canonical rules for plant organ biomass partitioning and growth allocation. Am. J. Bot. 89, 812–819. doi: 10.3732/ajb.89.5.812
Normand, F., Bissery, C., Damour, G., and Lauri, P.-E. (2008). Hydraulic and mechanical stem properties affect leaf-stem allometry in mango cultivars. New Phytol. 178, 590–602. doi: 10.1111/j.1469-8137.2008.02380.x
Ogawa, K. (2008). The leaf mass/number trade-off of Kleiman and Aarssen implies constancy of leaf biomass, its density and carbon uptake in forest stands: scaling up from shoot to stand level. J. Ecol. 96, 188–191.
Olson, M. E., Aguirre-Hernández, R., and Rosell, J. A. (2009). Universal foliage-stem scaling across environments and species in dicot trees: plasticity, biomechanics and Corner’s Rules. Ecol. Lett. 12, 210–219. doi: 10.1111/j.1461-0248.2008.01275.x
Poorter, L., and Rozendaal, D. M. A. (2008). Leaf size and leaf display of thirty-eight tropical tree species. Oecologia 158, 35–46. doi: 10.1007/s00442-008-1131-x
Preston, K. A., and Ackerly, D. D. (2003). Hydraulic architecture and the evolution of shoot allometry in contrasting climates. Am. J. Bot. 90, 1502–1512. doi: 10.3732/ajb.90.10.1502
Preston, K. A., Cornwell, W. K., and DeNoyer, J. L. (2006). Wood density and vessel traits as distinct correlates of ecological strategy in 51 California coast range angiosperms. New Phytol. 170, 807–818. doi: 10.1111/j.1469-8137.2006.01712.x
R Development Core Team (2004). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T. (1964). A quantitative analysis of plant form – the pipe model theory. I. basic analysis. Jpn. J. Ecol. 14, 97–105.
Smith, D. D., Sperry, J. S., and Adler, F. R. (2017). Convergence in leaf size versus twig leaf area scaling: do plants optimize leaf area partitioning? Ann. Bot. 119, 447–456. doi: 10.1093/aob/mcw231
Sperry, J. S., Hacke, H. G., and Pittermann, J. (2006). Size and function in conifer tracheids and angiosperm vessels. Am. J. Bot. 93, 1490–1500. doi: 10.3732/ajb.93.10.1490
Sperry, J. S., Meinzer, F. C., and McCulloh, K. A. (2008). Safety and efficiency conflicts in hydraulic architecture: scaling from tissues to trees. Plant Cell Environ. 31, 632–645. doi: 10.1111/j.1365-3040.2007.01765.x
Sun, S.-C., Jin, D.-M., and Shi, P.-L. (2006). The leaf size – twig size spectrum of temperate woody species along an altitudinal gradient: an invariant allometric scaling relationship. Ann. Bot. 97, 97–107. doi: 10.1093/aob/mcj004
Tamura, K., Dudley, J., Nei, M., and Kumar, S. (2007). MEGA4: molecular evolutionary genetics analysis MEGA) software version 4.0. Mol. Biol. Evol. 24, 1596–1599. doi: 10.1093/molbev/msm092
Tyree, M. T., and Zimmermann, M. H. (2002). Xylem Structure and the Ascent of Sap, 2nd Edn. Berlin: Springer. doi: 10.1007/978-3-662-04931-0
Warton, D. I., Wright, I. J., Falster, D. S., and Westoby, M. (2006). Bivariate line-fitting methods for allometry. Biol. Rev. 81, 259–291. doi: 10.1017/S1464793106007007
Westoby, M., Falster, D. S., Moles, A. T., Vesk, P. A., and Wright, I. J. (2002). Plant ecology strategies: some leading dimensions of variation between species. Ann. Rev. Ecol. Syst. 33, 125–149. doi: 10.1146/annurev.ecolsys.33.010802.150452
Westoby, M., and Wright, I. J. (2003). The leaf size – twig size spectrum and its relationship to other important spectra of variation among species. Oecologia 135, 621–628. doi: 10.1007/s00442-003-1231-6
White, P. S. (1983a). Corner’s rules in eastern deciduous trees: allometry and its implications for the adaptive architecture of trees. Bull. Torrey Bot. Club 110, 203–212. doi: 10.2307/2996342
White, P. S. (1983b). Evidence that temperature east North American evergreen woody plants follow Corner’s rules. New Phytol. 95, 139–145. doi: 10.1111/j.1469-8137.1983.tb03477.x
Wright, I. J., Falster, D. S., Pickup, M., and Westoby, M. (2006). Cross-species patterns in the coordination between leaf and stem traits, and their implications for plant hydraulics. Physiol. Plant. 127, 445–456. doi: 10.1111/j.1399-3054.2006.00699.x
Xiang, S., Wu, N., and Sun, S. (2010). Testing the generality of the ‘leafing intensity premium’ hypothesis in temperate broad-leaved forests: a survey of variation in leaf size within and between habitats. Evol. Ecol. 24, 685–701. doi: 10.1007/s10682-009-9325-1
Xu, L., Harrison, R. D., Yang, P., and Yang, D. R. (2011). New insight into the phylogenetic and biogeographic history of genus Ficus: vicariance played a relatively minor role compared with ecological opportunity and dispersal. J. Syst. Evol. 49, 546–557. doi: 10.1111/j.1759-6831.2011.00155.x
Yan, E.-R., Milla, R. R., Aarssen, L. W., and Wang, X.-H. (2012). Functional relationships of leafing intensity to plant height, growth form and leaf habit. Acta Oecol. 41, 20–29. doi: 10.1016/j.actao.2012.04.001
Yang, D. M., Li, G. Y., and Sun, S. C. (2008). The generality of leaf size versus number trade-off in temperate woody species. Ann. Bot. 102, 623–629. doi: 10.1093/aob/mcn135
Yang, D. M., Niklas, K. J., Xiang, S., and Sun, S. C. (2010). Size-dependent leaf area ratio in plant twigs: implication for leaf size optimization. Ann. Bot. 105, 71–77. doi: 10.1093/aob/mcp262
Zanne, A. E., Westoby, M., Falster, D. S., Ackerly, D. D., Loarie, S. R., Arnold, S. J., et al. (2010). Angiosperm wood structure: global patterns in vessel anatomy and their relation to wood density and potential conductivity. Am. J. Bot. 92, 207–215. doi: 10.3732/ajb.0900178
Keywords: biomass allocation, Ficus, theoretical hydraulic conductivity, leaf–stem relationship, mechanical strength, trade-off, wood density
Citation: Fan Z-X, Sterck F, Zhang S-B, Fu P-L and Hao G-Y (2017) Tradeoff between Stem Hydraulic Efficiency and Mechanical Strength Affects Leaf–Stem Allometry in 28 Ficus Tree Species. Front. Plant Sci. 8:1619. doi: 10.3389/fpls.2017.01619
Received: 04 June 2017; Accepted: 04 September 2017;
Published: 20 September 2017.
Edited by:
Boris Rewald, University of Natural Resources and Life Sciences, Vienna, AustriaCopyright © 2017 Fan, Sterck, Zhang, Fu and Hao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ze-Xin Fan, ZmFuemV4aW5AeHRiZy5vcmcuY24=
 Ze-Xin Fan
Ze-Xin Fan Frank Sterck
Frank Sterck Shi-Bao Zhang
Shi-Bao Zhang Pei-Li Fu
Pei-Li Fu Guang-You Hao
Guang-You Hao