- John Curtin School of Medical Research, The Australian National University, Canberra, ACT, Australia
by Tcherkez, G.G., Bathellier, C., Farquhar, G.D., and Lorimer, G. H. (2018). Front. Plant Sci. 9:929. doi: 10.3389/fpls.2018.00929
Introduction
Understanding the molecular mechanisms that make enzymes work remains one of the grand challenges in contemporary biophysics. If this understanding can be translated into the successful re-engineering of enzymes with greater efficiency, the practical benefits could be enormous. One such enzyme that has been targeted for re-engineering, ribulose 1,5-bisphosphate carboxylase/oxygenase (Rubisco, EC 4.1.1.39), is of intensive interest in agriculture and related fields as it fixes CO2 in higher plants and the vast majority of other photosynthetic organisms. In a recent article, Cummins et al. (2018a), we presented a statistical analysis of a wide range of published kinetic data on Rubisco. The results of that study suggested evidence of significant rates of decarboxylation (reaction with CO2) and deoxygenation (from the side reaction of Rubisco with O2) among wild-type Rubiscos. These results have challenged the accepted view that dissociation of the gas molecules (decarboxylation and deoxygenation) from the enzyme complex is negligible in all wild-type Rubiscos. In a commentary on Cummins et al. (2018a), Tcherkez et al. (2018) have contested our conclusion of significant decarboxylation and deoxygenation rates in Rubisco and suggested it is based on a misinterpretation of “implicit relationships between Rubisco rate constants” and “overlooks experimental evidence for feeble rates of deoxygenation and decarboxylation.” In this response to their commentary on Cummins et al. (2018a), we address these criticisms.
Interpretation of Rate Constants
Firstly, it is necessary to clarify the significance of γ, a parameter which arises from explicitly including the rate of product release in the kinetic scheme (Figure 1 in Cummins et al., 2018a). The equation for carboxylation is given by (see Supplementary Material in Cummins et al., 2018a but expressed in the form x/(y + x)),
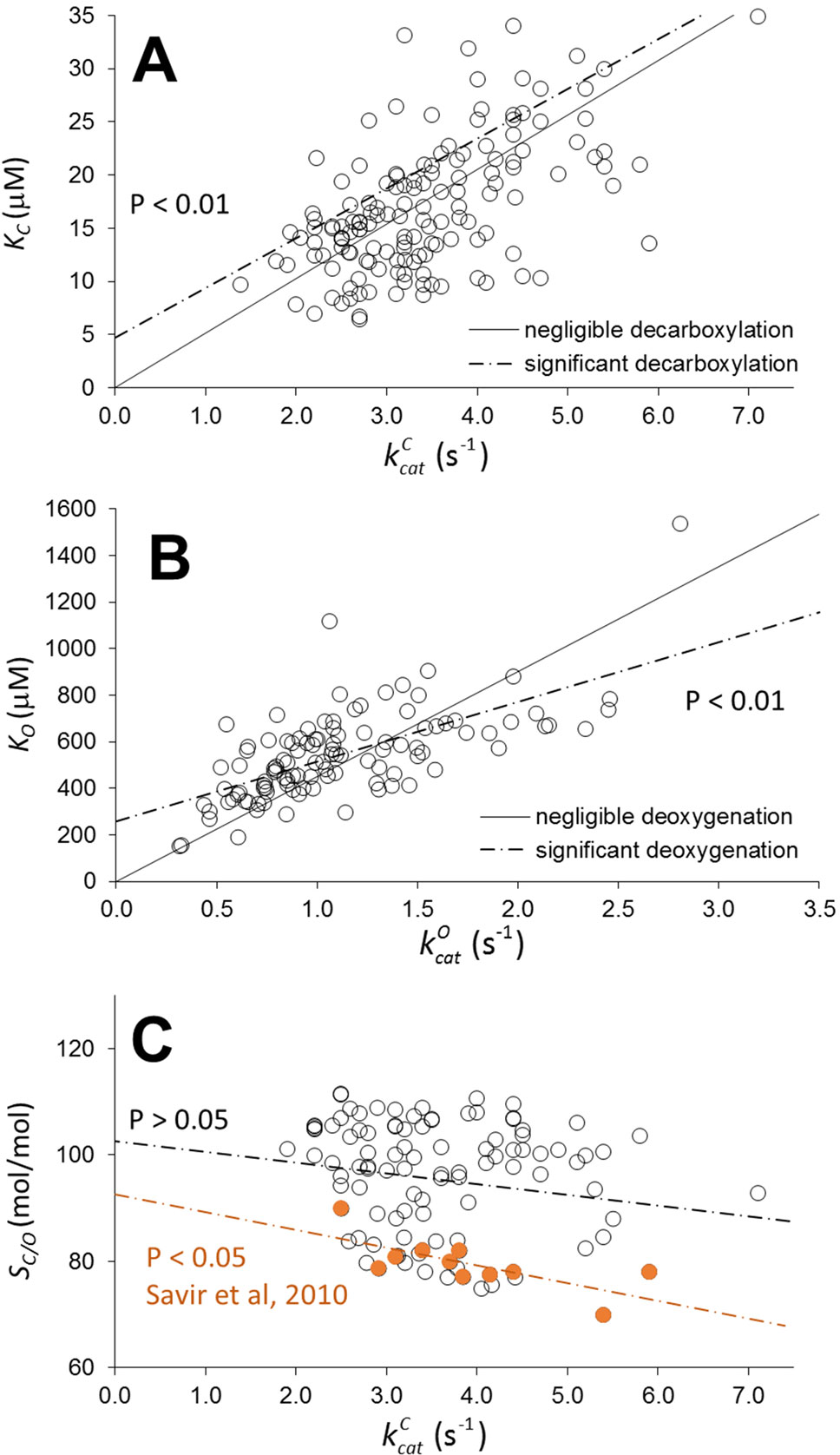
Figure 1 Scatter plots of KC as a function of (A), KO as a function of (B), and relative specificity, SC/0, as a function of (C) for wild type in higher-plant Rubiscos from various data compilations (Ishikawa et al., 2009; Galmés et al., 2014; Orr et al., 2016; Prins et al., 2016; Cummins et al., 2018a). Assuming decarboxylation and deoxygenation are negligible in all Rubiscos, the solid lines (with zero intercept) were obtained by optimizing only the coefficients of and in the linear regression. The dashed lines were obtained by optimizing both the coefficient and intercept in the linear regression. Deviation of the dashed line from the solid line is statistically significant (with non-zero intercept, P< 0.01). From Equation 2, the intercepts are the product of the expected (estimation of the mean) values < k-m > and the corresponding slopes (1/< KRk6>). If the intercept is non-zero, < k-m > must also be non-zero, indicating the high likelihood of decarboxylation and deoxygenation in a significantly large number of Rubiscos. Furthermore, we have reproduced the trade-off between SC/0 and (C), from the data of Savir et al. (2010) used to demonstrate “optimality in a low dimensional landscape”; this shows that it is not mirrored when a larger sampling of data for plant Rubiscos is used.
where k9 is the rate of product release, k3 rate of enolization, and k7 rate of product formation (k7/k8 is the equilibrium constant for enzyme-bound product formation). If only product release (k9) is rate limiting and the k7/k8 equilibrium is achieved rapidly (k9≪k8) then γC=k8/(k7+k8) must be a relatively small number (<< 1) as equilibrium strongly favors formation of the product. However, there is no evidence that product release limits the reaction, so we need not consider it further. If, as expected, hydration/cleavage (k7) is rate limiting, or co-limits with enolization (k3) then clearly γC≈1 and consequently, it is erroneous to suggest (Tcherkez et al., 2018) that “ γC must be a relatively small number.” Exactly the same arguments apply to the oxygenation reaction, and thus γO≈1. Secondly, we do not “disregard conditions of validity to perform a Taylor expansion.” The linear equation is clearly a reasonable approximation (Equation 1, Figures 2A, B in Cummins et al. 2018a) for Rubiscos with low enough kcat, i.e., where higher-order terms in the expansion diminish. We do not make any claim that the expected values of kinetic constants estimated in this way are valid where the variation in KC becomes rapid as kcat increases. We address the second question raised in Table 1 in Tcherkez et al. (2018) as follows:
Is enolization variable and thus can KR (and γC ) change a lot between Rubiscos? We agree that the answer to this question in Table 1 in Tcherkez et al. (2018) is “yes,” but this is precisely why statistical analysis should be applied. Consequently, the two points raised in relation to this question seem to us irrelevant. The “constant” values for the coefficients obtained from the regression analysis do not imply, as Tcherkez et al. (2018) seem to suggest, constant values for the underlying rate constants which we all agree will obviously vary among Rubiscos. It must be emphasized that the coefficients (together with their confidence intervals) should be interpreted as an estimation of a population mean (expected value) of rate constants (or functions thereof, e.g., 1/KRk6) based on a limited sample of Rubiscos. Thus, the estimation of mean decarboxylation and deoxygenation rates varies over a range of values defined by the confidence intervals (Table 3, in Cummins et al., 2018a). While the increase in KC over the entire range of kcat appears exponential, variations are likely to be more linear within a given taxonomic group. The main limitation of the regression analysis is the availability of a sample that is representative of the population distribution within a taxonomic group. The fact that linear regression is representative of the higher plant data is demonstrated below using a more extensive Rubisco sampling.
Linear Regression Is Representative of the Data
In essence, Cummins et al. (2018a) is not an attempt to “extract implicit rate constants.” Except perhaps for k7 if rate limiting), it is impossible to determine rate constants for specific Rubiscos from the kinetic data. Rather, it is sufficient to infer whether linear regression is representative of the data by applying hypothesis testing based on analysis of variance (ANOVA) to the coefficient and intercept, which are both functions of the implicit rate constants according to the kinetic mechanism (Equations 1 and 2 in Cummins et al., 2018a). However, recognizing that the sample sizes may not be representative (Table 1 in Tcherkez et al., 2018; Cummins et al., 2018a) of the population, we have searched the literature for more data. Figure 1 illustrates the application of the linear regression analysis to a wider-ranging set of carboxylation and oxygenation data (including Table 1 from Tcherkez et al., 2018; Cummins et al., 2018a) for wild-type Rubiscos in higher plants assembled from various sources (Galmés et al., 2014; Prins et al., 2016; Orr et al., 2016; Ishikawa et al., 2009). The general equation which relates the regression coefficients to the rate constants can be written as (Equations 1 and 2 in Cummins et al., 2018a, where here for clarity we have made the substitutions γC=γO=1, k6=k-C , k5=k+C , k12 = k-O and k11 = k+O)
Thus k+m and k-m are, respectively, the binding and dissociation rate constants for CO2 or O2. The linear increase in the observed Km as a function of is clearly apparent in Figure 1 (P < 0.01 for the coefficient). Note, however, that the carboxylation data (A) exhibit a very high degree of heteroscedasticity, with the residuals expanding as increases, indicating increasing variance in k-C and KRk+C and specificity, . If there is negligible dissociation ( for all wild-type Rubiscos), the variation in Km can only arise from KRk+m. If there is significant CO2 and O2 dissociation, the scatter in the plots derives from variations in both k-m and KRk+m. From the results in Figure 1, it is more likely than not that the intercept of the regression line (dashed lines) is non-zero (P < 0.01), indicating decarboxylation and deoxygenation do have an effect on Km. It is important to note, however, due to possible variations between and k-m that the influence of decarboxylation and deoxygenation on kinetic behavior does not necessarily apply to all Rubiscos. Consequently, we might expect to see a range of commitments, or partitioning between reaction intermediate and product, p (McNevin et al., 2007),
in wild-type plants ranging from perhaps as low as 50–60% up to 90–100%, depending on the effect of sequence variation on the rates of gas dissociation and catalysis.
Experimental Evidence Against Decarboxylation and Deoxygenation
Notwithstanding that our analysis does suggest negligible rates of decarboxylation and deoxygenation are likely to be found in many Rubiscos, we feel it appropriate to comment on the experimental evidence put forward by Tcherkez et al. (2018). The “direct evidence” against deoxygenation and decarboxylation (Table 1 in Tcherkez et al. (2018) is in reality interpretations of various experiments and not definitive experimental findings. We address each of the points raised under the first and third questions in Table 1 in Tcherkez et al. (2018) as follows:
Is the Decarboxylation Rate of Importance?
Point 1: Hydrolysis of the isolated reaction intermediate 3-keto-2′-carboxyarabinitol-1,5-bisphosphate (CKABP), which is relatively stable in solution, proceeds without significant decarboxylation, although its catalytic rate is poor (slower by a factor of ∼50) compared with RuBP (Lorimer et al., 1986). Lorimer et al. (1986) suggest the slower catalysis for CKABP may be due to a conformational change (presumably leaving decarboxylation unaffected). It should be noted, however, that to mimic the actual reaction, the enzyme–substrate complex should also be in an appropriate protonation state (Cummins et al., 2018b). Subsequent to enolization of RuBP, the proton on the O3 carbon of substrate needs to be transferred to the enzyme in order to form the C3-carbonyl group as in CKABP. Thus, post-carboxylation, there is one less proton in the CKABP intermediate compared with RuBP (carbonyl O3 vs hydroxyl O3), and the enzyme active site has one additional proton, most probably on HIS294 (Tcherkez et al., 2013; Cummins et al., 2018b), compared with the state at RuBP binding. Coincidentally, the tight-binding inhibitor (2CABP) found in most crystal structures of Rubisco also has a C3-hydroxyl group as in RuBP and binds to the Rubisco active site in the right conformation despite having the C2-carboxylate group. The proton exchange between the intermediate compound and enzyme during the natural forward reaction would need to be reversed for the backward reaction from CKABP to RuBP to proceed. However, there is apparently an incompatibility when the starting state of the enzyme (without the additional proton to mimic the transaction during enolization) binds the reaction intermediate CKABP, which is probably responsible for slowing down the forward processing of CKABP by up to a factor of 50 (Lorimer et al., 1986) and may also inhibit decarboxylation. Thus, the experiments of Lorimer et al. (1986) are in essence evidence for negligible decarboxylation in CKABP, not for dissociation of CO2 in carboxylated RuBP. Nevertheless, if the assumptions of Lorimer et al. (1986) are correct, their findings for one plant Rubisco (spinach) and the inferences drawn from regression analysis (Figure 1) are not necessarily inconsistent, as the latter does not preclude potentially many other plant Rubiscos with negligible decarboxylation.
Point 2: Interpretation of the measured kinetic isotope effects in Rubisco (αRubisco) in terms of the partitioning for CKABP, p (Equation 3), using the equation (McNevin et al., 2007),
relies heavily on knowledge of the intrinsic isotopic ratios for both the carboxylation (αcarb) and decarboxylation (αdecarb) rate constants, which cannot be measured directly and have been variously assumed or estimated: αdecarb=1.07 (McNevin et al., 2007, Tcherkez et al., 2018) or αdecarb=1.04 (Tcherkez et al., 2013).
Is the Deoxygenation Rate of Importance?
Point 1: Our recent computational study (Kannappan et al., 2019) suggests that rates of catalysis and deoxygenation may well be very similar. The overall reaction, i.e., to products, is certainly highly exothermic, so it clearly cannot be reversed. However, this should not be confused with the first part of the reaction involving binding of the oxygen to the enediolate of RuBP (a determinant of KO), which was found to be only moderately exothermic—in contrast to the assertion of Tcherkez—thus permitting the possibility of dissociation rates comparable with catalytic rates. As elaborated next in Point 2, the peroxo adduct formed by the hitherto unknown mechanism reported by Kannappan et al. is a strongly stabilized anion with structure (e.g., bond lengths) very different from isolated peroxides. Thus, references to peroxides in general are not relevant; a thermodynamically stable peroxo adduct would have too high a barrier for progression to the next step.
Point 2: The argument that electron spin should explain negligible deoxygenation is ill-conceived because the reverse, i.e., oxygenation, the binding of oxygen to the enediolate of RuBP, must also be spin forbidden. It is possible that both binding and dissociation are feasible by flipping between singlet and triplet states where the energy surfaces crossover (intersystem crossing). This has been verified by our quantum chemical calculations (Kannappan et al., 2019). Note that this is the first study in the literature that has addressed directly how the formally spin-forbidden oxygenation step (triplet O2 to singlet peroxo adduct) can be achieved. The mechanism, via a caged biradical enediolate–O2 complex, indicates Rubisco is a unique type of oxygenase without precedent in the literature.
Point 3: As discussed for decarboxylation above, intrinsic isotopic ratios are often uncertain.
In summary, there are no direct and conclusive measurements of decarboxylation and deoxygenation rate constants, only inferences drawn from other experimental results.
Conclusions
Although precise determinations of both decarboxylation and deoxygenation rate constants for specific Rubiscos are non-existent, our inferential statistical analysis (Figure 1 and Cummins et al., 2018a) of the available kinetic data for higher plants suggests that a significant number of wild-type Rubiscos (but by no means all) likely exhibit decarboxylation and/or deoxygenation that will have a significant negative impact on commitment of CKABP to form product (Equation 3). The results (Figure 1) clearly demonstrate that linear regression is representative of the higher-plant wild types for which there are a relative abundance of published data. As is now apparent in the published literature on Rubisco kinetics, as more data come to light, levels of variance far greater than previously expected (Tcherkez et al., 2006; Savir et al., 2010) are now being found. From our analysis based on a sample of approximately 150 Rubiscos (Figure 1), the population of higher plants is expected to exhibit a wide range of decarboxylation behavior. Further research is necessary not only into the diversity in higher-plant Rubisco kinetics but also into the kinetics for a wider variety of Rubisco taxonomic forms, which is currently lacking (Hanson, 2016). For the design of efficient Rubiscos, it is important to gain a comprehensive understanding of the nature of the constraints that cause the apparent trade-off in carboxylation rate and relative specificity (SC/O). The recent directed-evolution studies (Gomez-Fernandez et al., 2018; Wilson et al., 2018) that have reported deviations from this trade-off provide one avenue in this direction. Moreover, it appears that higher plants are not so constrained, as the trade-off is not clearly evident from a much broader sample (Figure 1). This conclusion is supported more broadly by a comprehensive statistical analysis of all the kinetic data (Flamholz et al., 2018, Flamholz et al., 2019). However, there are currently insufficient data for all non-plant Rubiscos to be able to judge whether these findings can be generalized. A more precise explanation of Rubisco catalysis, possibly in terms of sequence variation in the preorganization of charged, polar, and nonpolar groups (Warshel et al., 2006; Frushicheva et al., 2014; Jindal and Warshel, 2017), may be required to rationalize these disparate experimental results. As we have already discussed (Cummins et al., 2018a), such kinetic behavior may well be explained by selection mechanisms (Studer et al., 2014), rather than by the interdependence of implicit rate constants (Tcherkez et al., 2006, Tcherkez et al., 2018). The assertion (Tcherkez et al., 2018) that Lys166 can be used to rationalize the interdependence of rate constants is not supported by our recent study (Cummins et al., 2019) on the final stereospecific protonation step of the carboxylase reaction.
Author Contributions
PC, BK, and JG prepared the response and approved it for submission.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Cummins, P. L., Kannappan, B., Gready, J. E. (2018a). Directions for optimization of photosynthetic carbon fixation: Rubisco’s efficiency may not be so constrained after all. Front. Plant Sci. 9, 183. doi: 10.3389/fpls.2018.00183
Cummins, P. L., Kannappan, B., Gready, J. E. (2018b). Revised mechanism of carboxylation of ribulose-1,5-biphosphate by Rubisco from large scale quantum chemical calculations. J. Comput. Chem. 39, 1656–1665. doi: 10.1002/jcc.25343
Cummins, P. L., Kannappan, B., Gready, J. E. (2019). Ab initio molecular dynamics simulation and energetics of the ribulose-1,5-biphosphate carboxylation reaction catalyzed by Rubisco: toward elucidating the stereospecific protonation mechanism. J. Phys. Chem. B 123, 2679–2686. doi: 10.1021/acs.jpcb.8b12088
Flamholz, A. I., Prywes, N., Moran, U., Davidi, D., Bar-On, Y. M., Oltrogge, L. M., et al. (2018). Revisiting tradeoffs in Rubisco kinetic parameters. bioRxiv. doi: 10.1101/470021.
Flamholz, A. I., Prywes, N., Moran, U., Davidi, D., Bar-On, Y. M., Oltrogge, L. M., et al. (2019). Revisiting tradeoffs in Rubisco kinetic parameters. Biochem. 58, 3365–3376. doi: 10.1021/acs.biochem.9b00237
Frushicheva, M. P., Mills, M. J. L., Schopf, P., Singh, M. K., Prasad, R. B., Warshel, A. (2014). Computer aided enzyme design and catalytic concepts. Curr. Opin. Chem. Biol. 21, 56–62. doi: 10.1016/j.cbpa.2014.03.022
Galmés, J., Kapralov, M. V., Andralojc, P. J., Conesa, M.À., Keys, A. J., Parry, M. A. J., et al. (2014). Expanding knowledge of the Rubisco kinetics variability in plant species: environmental and evolutionary trends. Plant Cell Environ. 37 (9), 1989–2001. doi: 10.1111/pce.12335
Gomez-Fernandez, B. J., Garcia-Ruiz, E., Martin-Diaz, J., Gomez de Santos, P., Santos-Moriano, P., Plou, F. J., et al. (2018). Directed -in vitro- evolution of precambrian and extant Rubiscos. Sci. Rep. 8. doi: 10.1038/s41598-018-23869-3
Hanson, D. T. (2016). Breaking the rules of Rubisco catalysis. J. Exp. Bot. 67 (11), 3180–3182. doi: 10.1093/jxb/erw197
Ishikawa, C., Hatanaka, T., Misoo, S., Fukayama, H. (2009). Screening of high kcat Rubisco among poaceae for improvement of photosynthetic CO2 assimilation in rice. Plant Prod. Sci. 12 (3), 345–350. doi: 10.1626/pps.12.345
Jindal, G., Warshel, A. (2017). Misunderstanding the preorganization concept can lead to confusions about the origin of enzyme catalysis. Proteins 85 (12), 2157–2161. doi: 10.1002/prot.25381
Kannappan, B., Cummins, P. L., Gready, J. E. (2019). Mechanism of oxygenase pathway reactions catalysed by Rubisco from large scale Kohn-Sham density functional calculations. J. Phys. Chem. B 123, 2833–2843. doi: 10.1021/acs.jpcb.9b00518
Lorimer, G. H., Andrews, T. J., Pierce, J., Schloss, J. V. (1986). 2′-carboxy-3-keto-D-arabinitol 1,5-bisphosphate, the six-carbon intermediate of the ribulose bisphosphate carboxylase reaction. Philos. Trans. R. Soc Lond. B Biol. Sci. 313, 397–407. doi: 10.1098/rstb.1986.0046
McNevin, D. B., Badger, M. R., Whitney, S. M., von Caemmerer, S., Tcherkez, G. G. B., Farquhar, G. D. (2007). Differences in carbon isotope discrimination of three variants of D-ribulose-1,5-bisphosphate carboxylase/oxygenase reflect differences in their catalytic mechanisms. J. Biol. Chem. 282 (49), 36068–36076. doi: 10.1074/jbc.M706274200
Orr, D. J., Alcântara, A., Kapralov, M. V., John Andralojc, P. J., Carmo-Silva, E., Parry, M. A. J. (2016). Surveying Rubisco diversity and temperature response to improve crop photosynthetic efficiency. Plant Physiol. 172, 707–717. doi: 10.1104/pp.16.00750
Prins, A., Orr, D. J., Andralojc, P. J., Reynolds, M. P., Carmo-Silva, E., Parry, M. A. J. (2016). Rubisco catalytic properties of wild and domesticated relatives provide scope for improving wheat photosynthesis. J. Exp. Bot. 67 (6), 1827–1838. doi: 10.1093/jxb/erv574
Savir, Y., Noor, E., Milo, R., Tlusty, T. (2010). Cross-species analysis traces adaptation of Rubisco toward optimality in a low-dimensional landscape. Proc. Natl. Acad. Sci. U.S.A. 107 (8), 3475–3480. doi: 10.1073/pnas.0911663107
Studer, R. A., Christin, P. A., Williams, M. A., Orengo, C. A. (2014). Stability-activity tradeoffs constrain the adaptive evolution of Rubisco. Proc. Natl. Acad. Sci. U.S.A. 111 (6), 2223–2228. doi: 10.1073/pnas.1310811111
Tcherkez, G. G. B., Bathellier, C., Stuart-Williams, H., Whitney, S., Gout, E., Bligny, R., et al. (2013). D2O solvent isotope effects suggest uniform energy barriers in ribulose-1,5-bisphosphate carboxylase/oxygenase catalysis. Biochem. 52, 869–877. doi: 10.1021/bi300933u
Tcherkez, G. G., Bathellier, C., Farquhar, G. D., Lorimer, G. H. (2018). Commentary: Directions for optimization of photosynthetic carbon fixation: Rubisco’s efficiency may not be so constrained after all. Front. Plant Sci. 9, 183. doi: 10.3389/fpls.2018.00183
Tcherkez, G. G., Farquhar, G. D., Andrews, T. J. (2006). Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized. Proc. Natl. Acad. Sci. U.S.A. 103 (19), 7246–7251. doi: 10.1073/pnas.0600605103
Warshel, A., Sharma, P. K., Kato, M., Xiang, Y., Liu, H., Olsson, M. H. M. (2006). Electrostatic basis for enzyme catalysis. Chem. Rev. 106, 3210–3235. doi: 10.1021/cr0503106
Keywords: RuBisCO, carbon fixation, photosynthesis, enzyme kinetics and specificity, protein evolution, evolutionary constraints, enzyme-complex stability, gas-substrate binding
Citation: Cummins PL, Kannappan B and Gready JE (2019) Response: Commentary: Directions for Optimization of Photosynthetic Carbon Fixation: RuBisCO’s Efficiency May Not Be So Constrained After All. Front. Plant Sci. 10:1426. doi: 10.3389/fpls.2019.01426
Received: 26 November 2018; Accepted: 15 October 2019;
Published: 22 November 2019.
Edited by:
Brian N. Bailey, University of California, Davis, United StatesReviewed by:
Juan Alejandro Perdomo Lopez, Lancaster University, United KingdomAnneke Prins, Middlesex University, United Kingdom
Copyright © 2019 Cummins, Kannappan and Gready. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter L. Cummins, cGV0ZXIuY3VtbWluc0BhbnUuZWR1LmF1
 Peter L. Cummins
Peter L. Cummins Babu Kannappan
Babu Kannappan Jill E. Gready
Jill E. Gready