- 1Queensland Alliance for Agriculture and Food Innovation, Centre for Crop Science, The University of Queensland, St Lucia, QLD, Australia
- 2Queensland Alliance for Agriculture and Food Innovation, Hermitage Research Facility, The University of Queensland, Warwick, QLD, Australia
- 3ARC Centre of Excellence for Plant Success in Nature and Agriculture, The University of Queensland, St Lucia, QLD, Australia
Genomic prediction of complex traits across environments, breeding cycles, and populations remains a challenge for plant breeding. A potential explanation for this is that underlying non-additive genetic (GxG) and genotype-by-environment (GxE) interactions generate allele substitution effects that are non-stationary across different contexts. Such non-stationary effects of alleles are either ignored or assumed to be implicitly captured by most gene-to-phenotype (G2P) maps used in genomic prediction. The implicit capture of non-stationary effects of alleles requires the G2P map to be re-estimated across different contexts. We discuss the development and application of hierarchical G2P maps that explicitly capture non-stationary effects of alleles and have successfully increased short-term prediction accuracy in plant breeding. These hierarchical G2P maps achieve increases in prediction accuracy by allowing intermediate processes such as other traits and environmental factors and their interactions to contribute to complex trait variation. However, long-term prediction remains a challenge. The plant breeding community should undertake complementary simulation and empirical experiments to interrogate various hierarchical G2P maps that connect GxG and GxE interactions simultaneously. The existing genetic correlation framework can be used to assess the magnitude of non-stationary effects of alleles and the predictive ability of these hierarchical G2P maps in long-term, multi-context genomic predictions of complex traits in plant breeding.
Introduction
Response to selection in breeding programs relies on predicting the additive genetic merit of new individuals for a target population of environments (Hallauer and Miranda, 1988; Comstock, 1996). Predicting the additive genetic merit of individuals, i.e., breeding values, requires the estimation of allele substitution effects of genetic loci (Falconer and Mackay, 1996). Both functional additive genetic effects and functional non-additive genetic effects, generated by interactions that exist within (dominance) and between (epistasis) genetic loci, contribute to estimates of allele substitution effects (Cheverud and Routman, 1996; Hill et al., 2008; Huang and Mackay, 2016). The contributions of functional additive effects to allele substitution effects are considered stationary as they are not influenced by changes in allele frequencies at genetic loci. However, the contributions of functional non-additive genetic effects (GxG interactions) to allele substitution effects are dependent on the allele frequencies of genetic loci. Therefore, changes in the genetic background can alter the predictions of allele substitution effects. Predictions of allele substitution effects can also change across environments, producing gene-by-environment (GxE) interactions. We refer to the alterations of allele substitution effects, and therefore predictions of the additive genetic merit of individuals in the presence of these interactions as non-stationary effects of alleles. In the most extreme case, allele substitution effects can change sign, i.e., from positive to negative values and vice versa, if changes in the value of non-stationary effects exceed the value of stationary effects (Paixão and Barton, 2016; Wientjes et al., 2021). Such sign changes in allele substitution effects change the performance landscape’s optimum and influence the breeding target (Wright, 1963; Messina et al., 2011). Therefore, breeding programs need to accurately predict these non-stationary effects of alleles across different contexts to deliver the highest possible response to selection. Beyond the theoretical considerations, we consider three contexts where the potential for change in sign of allele substitution effects was identified to influence genomic prediction accuracy for commercial maize breeding for the United States corn-belt (Cooper et al., 2014a,b): breeding cycles, populations, and environments. We anticipate these considerations will also be relevant for other plant breeding situations.
Non-stationary effects of alleles decrease the accuracy of genomic predictions across breeding cycles. The accuracy of genomic prediction decreases with an increase in breeding cycles between the training and prediction set (Clark et al., 2012; Pszczola et al., 2012; Daetwyler et al., 2013; Habier et al., 2013). Changes in genetic relationships, linkage disequilibrium, and causal loci’s cosegregation have been identified as important factors (Habier et al., 2013). These factors can impact GxG interactions due to changes in allele frequencies. A practical approach to account for GxG interactions in the decrease in genomic prediction accuracy over breeding cycles is periodic retraining of the genomic prediction equation (Podlich et al., 2004). However, this is costly and may exclude smaller breeding operations. The ability to estimate non-stationary effects of alleles can create opportunities to increase the persistence of prediction accuracy across breeding cycles and widen the application of genomic prediction in plant breeding.
Non-stationary effects of alleles decrease the accuracy of genomic predictions across populations. Genomic prediction across populations is important as the germplasm accessed for breeding applications is often organized in many different populations (Melchinger and Gumber, 1998; Technow et al., 2020; White et al., 2020). Across population prediction often suffers from lower accuracy than prediction across breeding cycles due to more considerable differences in allele frequencies of causal genetic loci (de Roos et al., 2009; Hayes et al., 2009). Along with mutations and redundancy of causal genetic loci, extreme differences in allele frequencies can cause discrepancies in segregation patterns of causal genetic loci between populations, which can cause large differences in allele substitution effects between populations (Rio et al., 2020). Empirical and simulation studies have shown that GxG interactions primarily determine these large changes in allele substitution effects between populations (Duenk et al., 2020; Legarra et al., 2020). Therefore, the ability to accurately capture GxG interactions in genomic prediction will be necessary to effectively utilize diverse germplasm (Tanksley and McCouch, 1997; Jordan et al., 2011; Mace et al., 2013, 2020; Gorjanc et al., 2016; Halewood et al., 2018).
Non-stationary effects of alleles decrease the accuracy of genomic predictions across environments. Genomic prediction across environments has allowed faster identification of stable performing varieties. Most methods that predict performance across environments, including GxE interactions, have been purely statistical (Yates and Cochran, 1938; Finlay and Wilkinson, 1963; Eberhart and Russell, 1966; Piepho, 1997; Burgueño et al., 2012; Crossa, 2012). With implicit knowledge of environmental effects, these methods have been shown to increase prediction accuracy within specific datasets or a well-defined target population of environments. Still, they are sensitive to changes in the target population of environments. Explicit knowledge of environmental effects can make genomic prediction across environments more robust. More recent methods have demonstrated improved prediction accuracy by explicitly including environmental covariates in genomic prediction (Heslot et al., 2014; Jarquín et al., 2014; Costa-Neto et al., 2021; Jarquin et al., 2021). However, all of these methods generate predictions conditional on current environments and therefore represent short-term predictions. Improved long-term predictions of response to selection in plant breeding, including effects of GxE interactions, will require methods to generate predictions of “best-bet” synthetic future environments (Hammer et al., 2020).
Despite the challenge of non-stationary effects of alleles, plant breeding has accurately predicted short-term response to selection to accumulate genetic gain over the long term (Duvick, 2005; Mackay et al., 2011). Short-term predictions of response to selection can mitigate non-stationary effects of alleles by conditioning predictions on current genetic backgrounds and environments. However, with the introduction of genomic prediction (Meuwissen et al., 2001), plant breeding now seeks to re-design breeding programs to further accelerate the pace of varietal development (Bernardo and Yu, 2007; Heffner et al., 2009; Gaynor et al., 2017). The increased speed of selection trajectories of new breeding strategies deploying genomic prediction places a stronger focus on plant breeding programs’ ability to predict long-term response to selection. Long-term predictions of response to selection struggle to mitigate the non-stationary effects of alleles, as predictions conditional on the current genetic background and environment become increasingly uninformative into the future. An illustrative simulation example to explore these concepts is provided in the Supplementary Information.
In this perspective, we discuss a few lessons learned from applying hierarchical gene-to-phenotype (G2P) maps in predictive breeding and our view of promising future research directions to realize improvements in the prediction of long-term response to selection in plant breeding.
Perspective
Improvements in prediction from the specification of interactions require thorough interrogation of the underlying G2P maps of complex traits (Houle et al., 2010; Marjoram et al., 2014). The genetic architecture of traits, which details the number, distribution of effect sizes, and “behavior” of these causal genetic variants, can be viewed as a G2P map. Therefore, the G2P map defines the complete paths from causal genetic variants to the phenotype of complex traits (Waddington, 1957; Burns, 1970; Lewontin, 1974). The dominant G2P map used to investigate the role of interactions in response to selection is a single complex trait underpinned by the infinitesimal model (Robertson, 1960; Carlborg et al., 2006; Hill et al., 2008; Mäki-Tanila and Hill, 2014; Goodnight, 2015; Paixão and Barton, 2016; Wientjes et al., 2021). The infinitesimal model allows breeders to consider complex phenotypes in a single trait context, with underlying genetic variation associated directly with the phenotypic variation of complex traits within a reference population of genotypes (Figure 1A). The infinitesimal model, embedded within the breeders equation (Lush, 1937), has been successful in plant breeding (Hallauer and Miranda, 1988; Comstock, 1996). However, alternative G2P maps have been developed. Here we consider their potential for breeding applications.
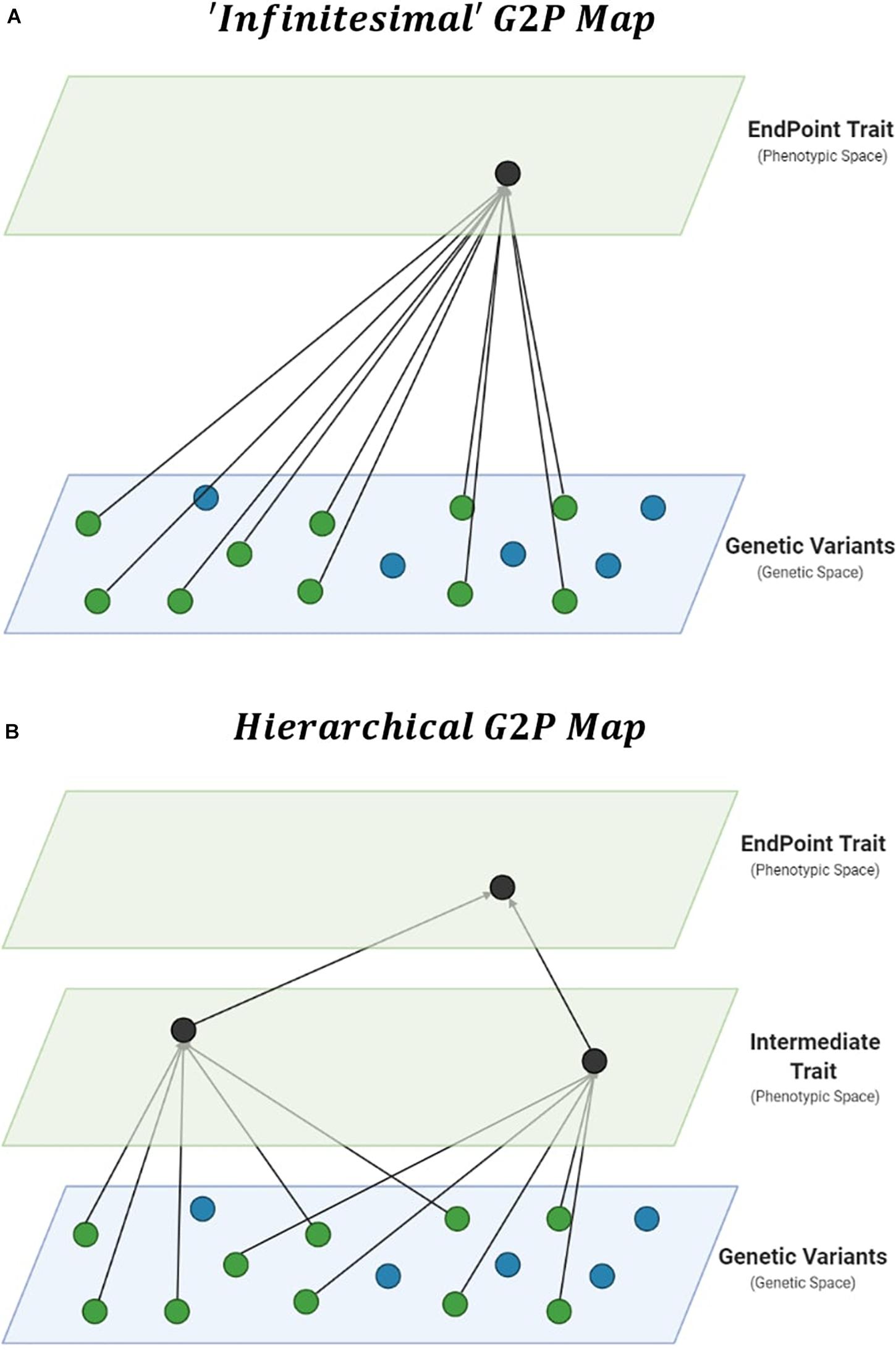
Figure 1. Gene-to-Phenotype (G2P) Maps. (A) Representation of an additive infinitesimal G2P map, assuming direct effects of causal genetic variants (green circles) on complex trait phenotypes. (B) Representation of an additive hierarchical G2P map, decomposing total effects into direct effects of causal genetic variants on intermediate traits, and phenotypic effects of multiple intermediate traits on complex trait phenotypes.
Hierarchical G2P maps provide a multi-trait context for investigations into the importance of interactions in genomic prediction. Complex trait phenotypes, such as grain yield, can be viewed as the product of multiple component traits. The hierarchical structure allows intermediate processes (Figure 1B), such as other traits and environmental factors and their interactions, to contribute to complex trait variation (Wright, 1934; Waddington, 1957; Houle et al., 2010; Liu et al., 2019; Cooper et al., 2020a).
In quantitative genetics, hierarchical G2P maps have been developed based on path analysis (Wright, 1934). The specification of intermediate processes in hierarchical G2P maps allows the decomposition of total effects, captured by the infinitesimal G2P map, into path specific direct and indirect effects (Wright, 1934). Lande and Arnold (1983) demonstrated that hierarchical G2P maps could be used to separate direct response to selection from indirect response to selection of multiple correlated traits. Valente et al. (2013) provide an overview of the breeding applications of Structural Equation Models (Gianola and Sorensen, 2004; Pearl, 2012) and highlight their ability to allow prediction across a broader range of livestock and crop management practices than standard multi-trait models without requiring frequent re-estimation of the G2P map. Recently, there has been an increase in the use of Structural Equation Models for prediction and inference in both animal and plant breeding (Tiezzi et al., 2015; Momen et al., 2018; Campbell et al., 2019; Pegolo et al., 2020; Abdalla et al., 2021). However, due to a lack of prior knowledge of the underlying relationships, most studies have used Structural Equation Models to estimate linear relationships between traits. The assumption of linear relationships restricts the range and magnitude of non-stationary effects and, therefore, the frequency of rank changes in additive genetic merit.
In plant science, decades of experiments led to the development of hierarchical G2P maps for plant breeding that allow predictions across a wide range of growing conditions (Holzworth et al., 2014; Hammer et al., 2019). Crop Growth Models are hierarchical mechanistic models of plants that simulate trajectories of multiple trait phenotypes over time for the growing season determined by environmental conditions. Crop Growth Models explicitly quantify the relationships, both linear and non-linear, between traits, physiological “meta-mechanisms” and complex trait phenotypes such as grain yield. These “meta-mechanisms” are measurable via high-throughput phenotyping and resulting in robust and stable equations with heritable genotype-dependent parameters (Tardieu et al., 2020). This has allowed Crop Growth Models to be linked to underlying genotypic variation for plant breeding applications (Chapman et al., 2003; Chenu et al., 2009; Messina et al., 2011). More recently, Crop Growth Model – Whole Genome Prediction methods have connected an underlying “infinitesimal” genetic architecture to key components of Crop Growth Models via a hierarchical Bayesian estimation procedure (Figure 2; Technow et al., 2015; Cooper et al., 2016). The inclusion of Crop Growth Models in genomic prediction enables the prediction of trait-trait and trait-environment interactions in the hierarchy’s upper levels, which are directly associated with the estimates of allele substitution effects of genetic parameters for traits in the lower levels of the crop growth model hierarchy. This correction of phenotypes can lead to improved estimates of genetic correlations between traits and increased prediction accuracies across the different contexts discussed above. Crop Growth Model – Whole Genome Prediction methods, and subsequent variations, have been shown to improve short-term predictions of genetic merit in the presence of GxE interactions (Bustos-Korts et al., 2019; Millet et al., 2019; Robert et al., 2020; Toda et al., 2020; Diepenbrock et al., 2021) and genotype-by-environment-by-management interactions in plant breeding. The success of hierarchical G2P maps in capturing non-stationary effects in predictions across diverse environments has seen growth models being revisited in animal breeding (Doeschl-Wilson et al., 2007; Puillet et al., 2016, 2021).
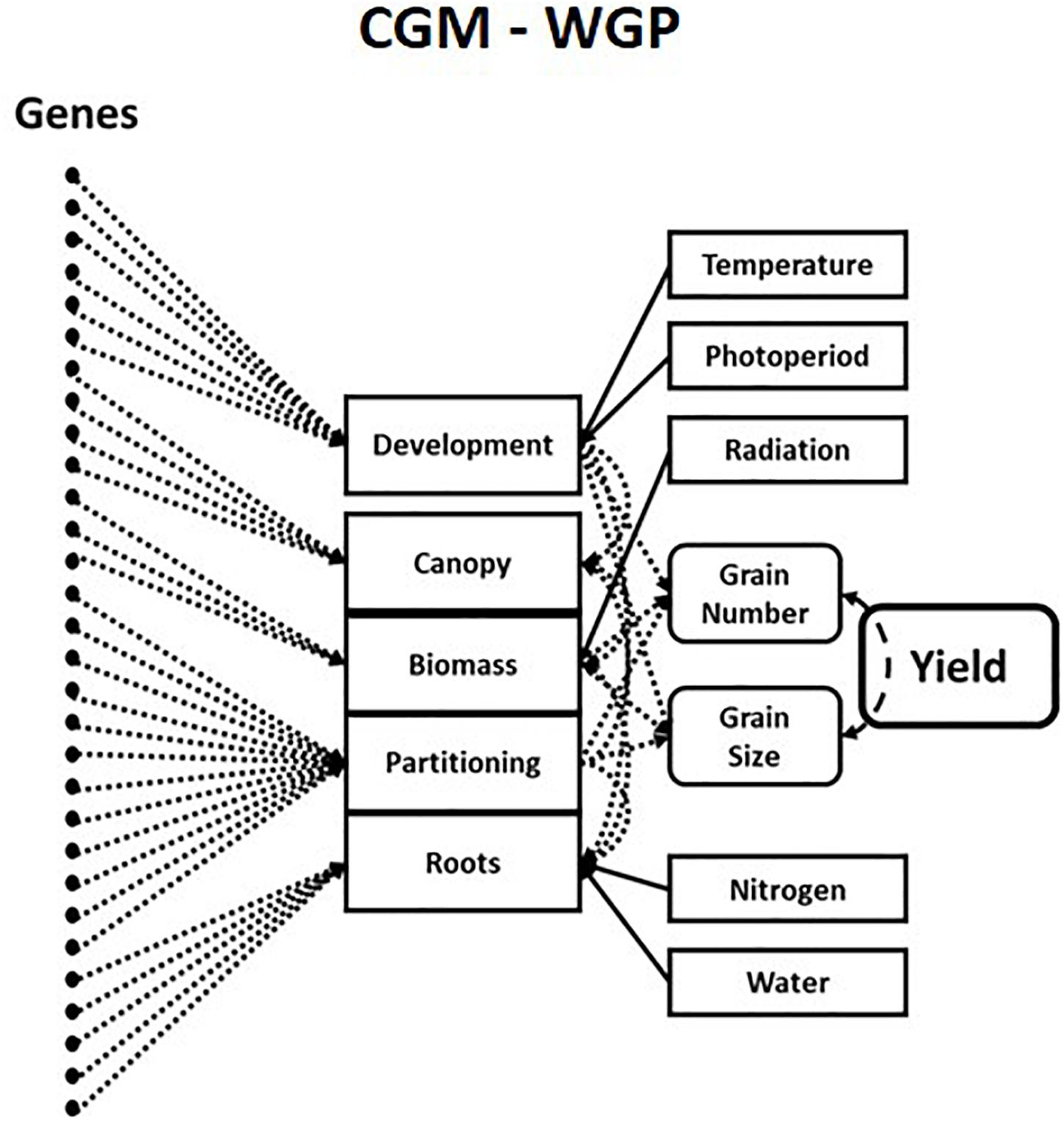
Figure 2. Schematic representation of a hierarchical crop growth model whole genome prediction (CGM-WGP) G2P map. Taken from Figure 2b of Cooper et al. (2020a). Genetic variants are associated with traits or “meta-mechanisms” at lower levels in the crop growth model hierarchy to predict traits at higher levels in the hierarchy.
However, the prediction of long-term response to selection remains a significant challenge (Reeve, 2000; Goddard, 2009; Hill, 2017). For example, long-term selection experiments in maize have often produced results not predictable a priori or from simulation (Lamkey, 1992; Dudley and Lambert, 2003), such as continued selection response after 100 years (Dudley and Lambert, 2003). Long-term predictions of response to selection, based on the classical versions of the infinitesimal model (Walsh and Lynch, 2018), struggle to accurately predict the non-stationary effects of alleles as information from current genetic backgrounds and environments become increasingly uninformative into the future. A key paper by Paixão and Barton (2016), extending Robertson’s (1960) work with only functional additive effects, has clarified the importance of non-stationary effects of alleles generated by GxG interactions for long-term response to selection. They describe two explicit scenarios: (i) when drift dominates selection, i.e., when the selection pressure at individual functional loci is weak, the initial variance components will determine the increase in response to selection over breeding cycles due to interactions; (ii) when selection dominates drift, i.e., when the selection pressure at individual functional loci is strong, the initial variance components are poor predictors of the response to selection over breeding cycles and details of the G2P map need to be explicitly considered. Therefore, to quantify the importance of non-stationary effects of alleles in predicting long-term response to selection in plant breeding, we should consider two questions:
i. What is the strength of selection operating on the causal loci for traits in breeding programs?
ii. If selection operating on the causal loci is strong, what is the underlying G2P map?
The availability of dense genotype data, sequence data, and advances in phenotyping provide the opportunity to revisit theories about the strength of selection in plant breeding programs. Before the ability to study allelic variation via genotype data, the selection units of breeding programs were breeding values of individuals. It has been shown for complex traits that strong selection at the individual level does not necessarily translate to strong selection at the causal loci (Goddard, 2009; Walsh and Lynch, 2018). However, technologies such as genomic prediction (Meuwissen et al., 2001) are shifting the selection units of breeding programs toward the allele substitution effects of genetic loci. Despite selection still occurring on individuals, genomic selection can distribute selection pressure unevenly across the genome by directing selection pressure to genetic loci with large estimated allele substitution effects (Heidaritabar et al., 2016; Wientjes et al., 2021). Therefore, the use of genomic selection in breeding programs can result in selection dominating drift at specific genetic loci placing greater importance on the G2P map assumed in genomic predictions.
Complete knowledge of the underlying G2P maps of complex traits is unlikely. However, hierarchical G2P maps with partial knowledge of intermediate processes offer promise for predicting long-term response to selection, given their success in improved short-term predictions of non-stationary effects of alleles. An obstacle in the practical applications of such hierarchical G2P modeling approaches is non-identifiability, also referred to as equifinality or the many-to-one property (Lamsal et al., 2018; Barghi et al., 2020; Henshaw et al., 2020; Kruijer et al., 2020; Tsutsumi-Morita et al., 2021). Effects can be non-identifiable due to unmeasured confounders that generate correlated errors between effects, which results in multiple, equally likely hierarchical G2P maps for experimental data sets. As an example, a multi-trait G2P map involving GxG interactions and the summation of Trait 1 and Trait 2 (Figure 3A) could equally be parameterized as the simplified Crop Growth Model – Whole Genome Prediction G2P map of two traits with purely additive functional genetic effects and non-linear relationships between traits (Figure 3B). Therefore, the level of detail required in hierarchical G2P maps to overcome non-identifiability is still an active research area.
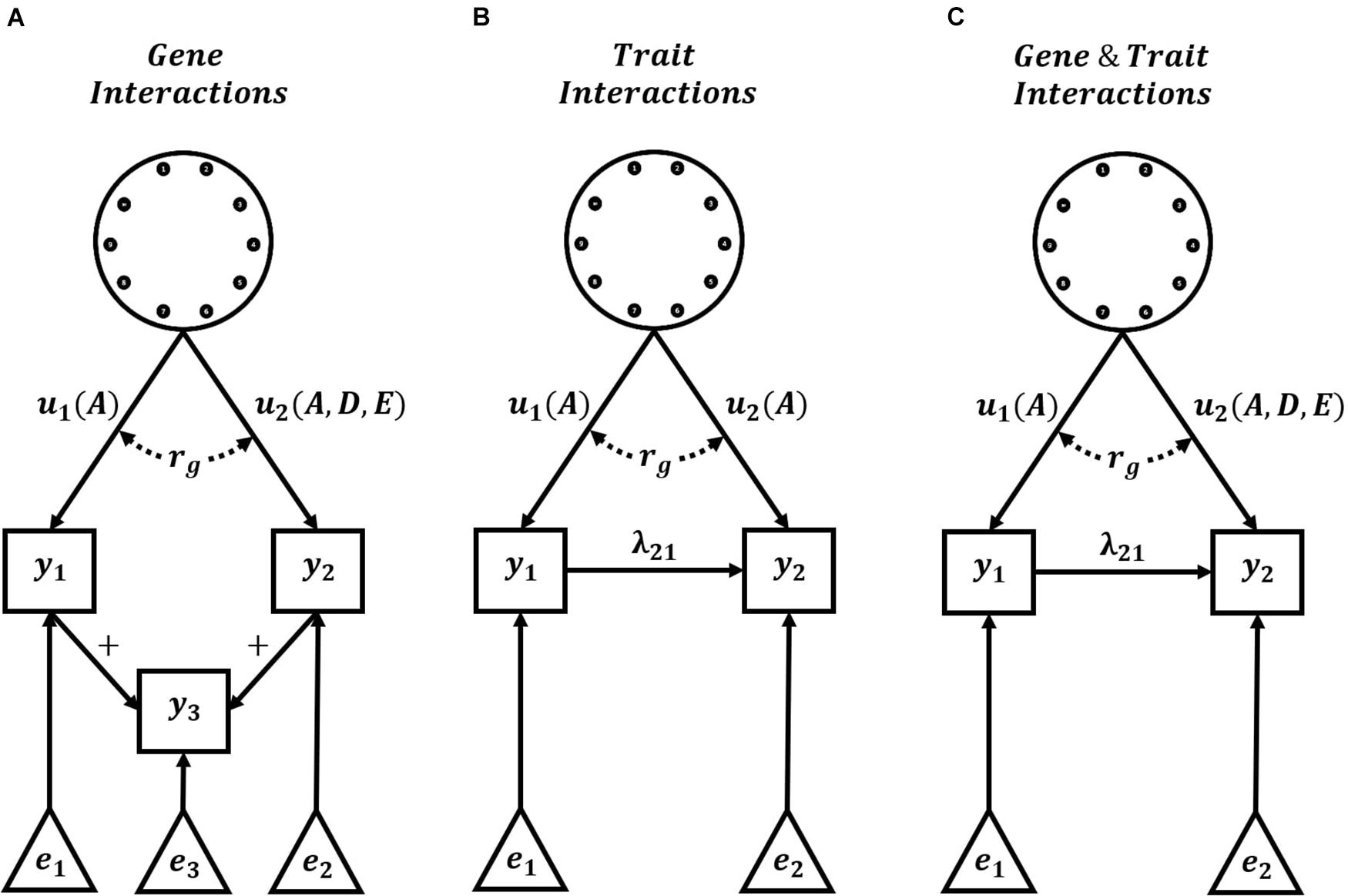
Figure 3. Hierarchical G2P Maps for Plant Breeding. Examples of three multi-trait hierarchical G2P maps with the explicit specification of interactions. Hierarchical G2P maps incorporating knowledge of trait interactions (+, λ) can be used to adjust phenotypes and increase the accuracy of the estimation of gene effects (u), gene interactions, and genetic correlations (rg) between traits. Gene effects (u) can be directly assigned to trait phenotypes (y) or indirectly assigned via linear trait relationships (+) or non-linear trait interactions (λ). A, D, and E indicate additive, dominance, and epistatic functional genetic effects, respectively. Non-genetic effects of trait phenotypes are represented by e. (A) Representation of a G2P map with gene interactions and linear relationship between trait phenotypes, (B) Representation of current Crop Growth Model – Whole Genome Prediction (CGM -WGP) G2P maps with additive genetic effects and non-linear trait interactions, and (C) Representation of potential G2P maps with both gene interactions and non-linear trait interactions.
Future Directions
In recent times, genomic prediction across multiple contexts has received increased focus in breeding (de Roos et al., 2009; Hayes et al., 2009; Windhausen et al., 2012; Gorjanc et al., 2016; Montesinos-López et al., 2019). In a multi-context setting, the genetic correlation naturally provides a measure to quantify predictive accuracy (Falconer, 1952; Robertson, 1959; Bohren et al., 1966). To maximize the benefits of using the genetic correlation framework, plant breeding requires hierarchical G2P maps that include the explicit specification of interactions (Figure 3C). Specification of gene-gene interactions would allow the assessment of changes in the genetic background on GxG interactions and prediction accuracy. Specification of gene-trait and trait-trait interactions would allow the assessment of changes in the environment and agronomic management on GxE interactions and prediction accuracy. Breeding programs are often organized in many different populations or regions to limit these impacts of GxG and GxE interactions, respectively, while assuming a single performance optimum and single breeding target. However, GxG or GxE interactions can generate a performance landscape with multiple optima (Wright, 1963; Cooper et al., 2005; Messina et al., 2011; Technow et al., 2020). Prior specification of this multiple optima landscape, via hierarchical G2P maps, would allow more comprehensive explorations of the impact of such interactions on the long-term response to selection of plant breeding programs.
Complementary simulation and empirical studies can interrogate the changes of genetic correlations across contexts to quantify the relative magnitude of GxG and GxE interactions and measure their impact on genomic prediction. Recent research, primarily from animal breeding, has renewed the focus on this framework (Wientjes et al., 2015; Dai et al., 2020; Duenk et al., 2020; Legarra et al., 2020). The common theme has been using the genetic correlation to assess likely magnitudes of GxG interactions underpinning complex traits. Duenk et al. (2020) used simulations to show that realistic levels of dominance alone could not drive the genetic correlation between two populations below 0.8, but realistic levels of epistasis could drive the genetic correlation as low as 0.45. Legarra et al. (2020) used two regularly intermated populations with similar allele frequencies and an expectation of minimal GxG interactions to speculate on the role of GxE in low across population predictions. They also suggested a genetic correlation threshold of 0.6, below which populations should be classed as distinct. However, these recent animal breeding studies overlooked the inclusion of GxE interaction scenarios. GxE interaction scenarios are of high relevance to plant breeding which regularly predict across a diverse set of target population of environments. Plant breeding is in a prime position to use results from evolutionary genetics (de Villemereuil et al., 2016), multi-environment trial analyses (Piepho, 1997; van Eeuwijk et al., 2005; Malosetti et al., 2013), and Crop Growth Models (Jones et al., 2003; Hammer et al., 2010; Messina et al., 2011; Holzworth et al., 2014) to assess the impact of GxE interactions on genetic correlations and determine their influence on breeding programs designed to utilize genomic prediction. Therefore, we propose that the plant breeding community undertake complementary simulation and empirical studies to quantify the relative magnitude of GxG and GxE interactions across relevant environmental and population contexts to quantify their impact on genomic prediction.
The dominant crop improvement procedure of today is a sequential operation. Breeding programs first develop new varieties with a limited sampling of the full range of farmers’ agronomic possibilities. Within this first step, plant breeding programs simultaneously perform population improvement to improve the additive genetic merit of breeding germplasm and product development, to identify new varieties with the highest total genotypic merit (Messina et al., 2011; Powell et al., 2020; Technow et al., 2020; Werner et al., 2020). Then agronomic research programs follow, focusing on developing and optimizing crop management strategies for the handful of new varieties. Hierarchical G2P maps can connect the objectives of plant breeding and quantitative genetics with those of crop agronomy (Figure 3; Cooper et al., 2020a,b). The explicit connections between gene and multiple trait levels, embedded in hierarchical G2P maps, can be perturbed experimentally (empirical and simulation) to quantify the impact of agronomic management interventions and changes in the environment. The effects of the perturbations can be investigated to determine how they propagate through the hierarchical G2P map and update estimates of allele effects at both the gene and trait levels. Ex-ante predictions of perturbations at the gene level could be used to guide improved prediction of “synthetic” varieties developed through novel gene-editing techniques. Ex-ante predictions of perturbations at the trait level could improve the efficiency of breeding new varieties adapted for alternative farming systems and future climate scenarios (Hammer et al., 2020). At the same time, predictions can be extracted from each level of the hierarchical G2P map, allowing the decomposition of individual performance into additive genetic, total genetic, and phenotypic merit. Decomposition of path-specific values in hierarchical G2P maps has been demonstrated in evolutionary and quantitative genetics (Lande and Arnold, 1983; Gianola and Sorensen, 2004; Valente et al., 2010, 2013; Henshaw et al., 2020; Janeiro et al., 2020; Pegolo et al., 2020). Therefore, the ability to exploit different sources of improved crop performance under a single prediction framework could improve crop improvement pipelines’ accuracy and flexibility to navigate performance landscapes for current and future environments (Messina et al., 2011, 2020; Technow et al., 2020).
Conclusion
Current genomic prediction methods struggle to predict the non-stationary effects of alleles as the genetic background (breeding cycles and populations) and the environment changes. These non-stationary effects of alleles are determined by interactions between genetic loci, traits, and the environment. Non-stationary effects of alleles result in low prediction accuracy across breeding cycles, populations and environments. As discussed above, the development of hierarchical G2P maps has been shown to improve the genomic prediction of non-stationary effects of alleles across breeding cycles and environments. The simultaneous specification of GxG and GxE interactions in hierarchical G2P maps may help to more thoroughly explore the impact of non-stationary effects of alleles on the long-term response to selection of plant breeding programs.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
OP and MC conceived and designed the perspective. OP wrote the first manuscript draft and developed the supporting simulations. MC, KV-F, DJ, and GH helped to refine the manuscript. All authors read and approved the final manuscript.
Funding
Contribution supported by the Australian Research Council Centre of Excellence for Plant Success in Nature and Agriculture (CE200100015) and the Australian Grains Research and Development Corporation project UOQ1903-008RTX. KV-F was supported by an Australian Research Council Discovery Early Career Research Award (DE210101407).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Information
A walkthrough of a simulation, data files, and scripts demonstrating non-stationary effects of alleles over breeding cycles can be accessed at https://powellow.github.io/Interactions_In_Breeding/.
References
Abdalla, E. A., Wood, B. J., and Baes, C. F. (2021). Accuracy of breeding values for production traits in turkeys (Meleagris gallopavo) using recursive models with or without genomics. Genet. Sel. Evol. 53:16. doi: 10.1186/s12711-021-00611-8
Barghi, N., Hermisson, J., and Schlötterer, C. (2020). Polygenic adaptation: a unifying framework to understand positive selection. Nat. Rev. Genet. 21, 769–781. doi: 10.1038/s41576-020-0250-z
Bernardo, R., and Yu, J. (2007). Prospects for genomewide selection for quantitative traits in maize. Crop. Sci. 47:1082. doi: 10.2135/cropsci2006.11.0690
Bohren, B. B., Hill, W. G., and Robertson, A. (1966). Some observations on asymmetrical correlated responses to selection. Genet. Res. 7, 44–57. doi: 10.1017/S0016672300009460
Burgueño, J., de los Campos, G., Weigel, K., and Crossa, J. (2012). Genomic prediction of breeding values when modeling genotype × environment interaction using pedigree and dense molecular markers. Crop. Sci. 52, 707–719. doi: 10.2135/cropsci2011.06.0299
Burns, J. (1970). “The synthetic problem and the genotype-phenotype relation in cellular metabolism,” in Towards a Theoretical Biology, ed C. H. Waddington (New Brunswick, NJ: Transaction Publishers), 47–51.
Bustos-Korts, D., Malosetti, M., Chenu, K., Chapman, S., Boer, M. P., Zheng, B., et al. (2019). From QTLs to adaptation landscapes: using genotype-to-phenotype models to characterize G×E over time. Front. Plant Sci. 10:1540. doi: 10.3389/fpls.2019.01540
Campbell, M. T., Yu, H., Momen, M., and Morota, G. (2019). Examining the relationships between phenotypic plasticity and local environments with genomic structural equation models. bioRxiv[perprint] doi: 10.1101/2019.12.11.873257
Carlborg, Ö, Jacobsson, L., Åhgren, P., Siegel, P., and Andersson, L. (2006). Epistasis and the release of genetic variation during long-term selection. Nat. Genet. 38, 418–420. doi: 10.1038/ng1761
Chapman, S., Cooper, M., Podlich, D., and Hammer, G. (2003). Evaluating plant breeding strategies by simulating gene action and dryland environment effects. Agron. J. 95, 99–113. doi: 10.2134/agronj2003.9900
Chenu, K., Chapman, S. C., Tardieu, F., McLean, G., Welcker, C., and Hammer, G. L. (2009). Simulating the yield impacts of organ-level quantitative trait loci associated with drought response in maize: a “““““gene-to-phenotype””””””. Mod. Approach. Genet. 183, 1507–1523. doi: 10.1534/genetics.109.105429
Cheverud, J. M., and Routman, E. J. (1996). Epistasis as a source of increased additive genetic variance at population bottlenecks. Evolution 50, 1042–1051. doi: 10.1111/j.1558-5646.1996.tb02345.x
Clark, S. A., Hickey, J. M., Daetwyler, H. D., and van der Werf, J. H. (2012). The importance of information on relatives for the prediction of genomic breeding values and the implications for the makeup of reference data sets in livestock breeding schemes. Genet. Sel. Evol. 44:4. doi: 10.1186/1297-9686-44-4
Comstock, R. E. (1996). Quantitative Genetics With Special Reference to Plant and Animal Breeding, 1st Edn. Ames: Iowa State University Press.
Cooper, M., Gho, C., Leafgren, R., Tang, T., and Messina, C. (2014a). Breeding drought-tolerant maize hybrids for the US corn-belt: discovery to product. J. Exp. Bot. 65, 6191–6204. doi: 10.1093/jxb/eru064
Cooper, M., Messina, C. D., Podlich, D., Totir, L. R., Baumgarten, A., Hausmann, N. J., et al. (2014b). Predicting the future of plant breeding: complementing empirical evaluation with genetic prediction. Crop Pasture Sci. 65, 311–336. doi: 10.1071/CP14007
Cooper, M., Podlich, D. W., and Smith, O. S. (2005). Gene-to-phenotype models and complex trait genetics. Aust. J. Agric. Res. 56, 895–918. doi: 10.1071/AR05154
Cooper, M., Powell, O., Voss-Fels, K. P., Messina, C. D., Gho, C., Podlich, D. W., et al. (2020a). Modelling selection response in plant breeding programs using crop models as mechanistic gene-to-phenotype (CGM-G2P) multi-trait link functions. Silico Plants 3: diaa016. doi: 10.1093/insilicoplants/diaa016
Cooper, M., Tang, T., Gho, C., Hart, T., Hammer, G., and Messina, C. (2020b). Integrating genetic gain and gap analysis to predict improvements in crop productivity. Crop Sci. 60, 582–604. doi: 10.1002/csc2.20109
Cooper, M., Technow, F., Messina, C., Gho, C., and Totir, L. R. (2016). Use of crop growth models with whole-genome prediction: application to a maize multienvironment trial. Crop Sci. 56, 2141–2156. doi: 10.2135/cropsci2015.08.0512
Costa-Neto, G., Fritsche-Neto, R., and Crossa, J. (2021). Nonlinear kernels, dominance, and envirotyping data increase the accuracy of genome-based prediction in multi-environment trials. Heredity 126, 92–106. doi: 10.1038/s41437-020-00353-1
Crossa, J. (2012). From genotype × environment interaction to gene × environment interaction. Curr. Genom. 13, 225–244. doi: 10.2174/138920212800543066
Daetwyler, H. D., Calus, M. P. L., Pong-Wong, R., de los Campos, G., and Hickey, J. M. (2013). Genomic prediction in animals and plants: simulation of data, validation, reporting, and benchmarking. Genetics 193, 347–365. doi: 10.1534/genetics.112.147983
Dai, Z., Long, N., and Huang, W. (2020). Influence of genetic interactions on polygenic prediction. G3amp58 Genes Genom. Genet. 10, 109–115. doi: 10.1534/g3.119.400812
de Roos, A. P. W., Hayes, B. J., and Goddard, M. E. (2009). Reliability of genomic predictions across multiple populations. Genetics 183, 1545–1553. doi: 10.1534/genetics.109.104935
de Villemereuil, P., Gaggiotti, O. E., Mouterde, M., and Till-Bottraud, I. (2016). Common garden experiments in the genomic era: new perspectives and opportunities. Heredity 116, 249–254. doi: 10.1038/hdy.2015.93
Diepenbrock, C., Tang, T., Jines, M., Technow, F., Lira, S., Podlich, D., et al. (2021). Can we harness digital technologies and physiology to hasten genetic gain in U.S. maize breeding? bioRxiv[preprint] doi: 10.1101/2021.02.23.432477
Doeschl-Wilson, A. B., Knap, P. W., Kinghorn, B. P., and Van der Steen, H. A. M. (2007). Using mechanistic animal growth models to estimate genetic parameters of biological traits. Animal 1, 489–499. doi: 10.1017/S1751731107691848
Dudley, J. W., and Lambert, R. J. (2003). “““““100 Generations of selection for oil and protein in corn””””,” in Plant Breeding Reviews, ed. J. Jules (John Wiley & Sons, Ltd), 79–110. doi: 10.1002/9780470650240.ch5
Duenk, P., Bijma, P., Calus, M. P. L., Wientjes, Y. C. J., and van der Werf, J. H. J. (2020). The impact of non-additive effects on the genetic correlation between populations. G3amp58 Genes Genom. Genet. 10, 783–795. doi: 10.1534/g3.119.400663
Duvick, D. N. (2005). Genetic progress in yield of united states maizE (Zea mays L.). Maydica 50, 193–202.
Eberhart, S. A., and Russell, W. A. (1966). Stability parameters for comparing varieties1. Crop Sci. 6, 36–40. doi: 10.2135/cropsci1966.0011183X000600010011x
Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. Harlow, UK: Longman.
Finlay, K., and Wilkinson, G. (1963). The analysis of adaptation in a plant-breeding programme. Aust. J. Agric. Res. 14:742. doi: 10.1071/AR9630742
Gaynor, R. C., Gorjanc, G., Bentley, A. R., Ober, E. S., Howell, P., Jackson, R., et al. (2017). A two-part strategy for using genomic selection to develop inbred lines. Crop Sci. 57, 2372–2386. doi: 10.2135/cropsci2016.09.0742
Gianola, D., and Sorensen, D. (2004). Quantitative genetic models for describing simultaneous and recursive relationships between phenotypes. Genetics 167, 1407–1424. doi: 10.1534/genetics.103.025734
Goddard, M. (2009). Genomic selection: prediction of accuracy and maximisation of long term response. Genetica 136, 245–257. doi: 10.1007/s10709-008-9308-0
Goodnight, C. (2015). Long-term selection experiments: epistasis and the response to selection. Methods Mol. Biol. Clifton NJ 1253, 1–18. doi: 10.1007/978-1-4939-2155-3_1
Gorjanc, G., Jenko, J., Hearne, S. J., and Hickey, J. M. (2016). Initiating maize pre-breeding programs using genomic selection to harness polygenic variation from landrace populations. BMC Genomics 17:30. doi: 10.1186/s12864-015-2345-z
Habier, D., Fernando, R. L., and Garrick, D. J. (2013). Genomic BLUP Decoded: a look into the black box of genomic prediction. Genetics 194, 597–607. doi: 10.1534/genetics.113.152207
Halewood, M., Chiurugwi, T., Sackville Hamilton, R., Kurtz, B., Marden, E., Welch, E., et al. (2018). Plant genetic resources for food and agriculture: opportunities and challenges emerging from the science and information technology revolution. New Phytol. 217, 1407–1419. doi: 10.1111/nph.14993
Hallauer, A. R., and Miranda, J. B. F. (1988). Quantitative Genetics in Maize Breeding, 2nd Edn. Ames: Iowa State University Press.
Hammer, G., Messina, C., Wu, A., and Cooper, M. (2019). Biological reality and parsimony in crop modelswhy we need both in crop improvement! Silico Plants 1:diz010. doi: 10.1093/insilicoplants/diz010
Hammer, G. L., McLean, G., Oosterom, E., van, Chapman, S., Zheng, B., et al. (2020). Designing crops for adaptation to the drought and high-temperature risks anticipated in future climates. Crop Sci. 60, 605–621. doi: 10.1002/csc2.20110
Hammer, G. L., van Oosterom, E., McLean, G., Chapman, S. C., Broad, I., Harland, P., et al. (2010). Adapting APSIM to model the physiology and genetics of complex adaptive traits in field crops. J. Exp. Bot. 61, 2185–2202. doi: 10.1093/jxb/erq095
Hayes, B. J., Bowman, P. J., Chamberlain, A. C., Verbyla, K., and Goddard, M. E. (2009). Accuracy of genomic breeding values in multi-breed dairy cattle populations. Genet. Sel. Evol. 41:51. doi: 10.1186/1297-9686-41-51
Heffner, E. L., Sorrells, M. E., and Jannink, J.-L. (2009). Genomic selection for crop improvement. Crop Sci. 49, 1–12. doi: 10.2135/cropsci2008.08.0512
Heidaritabar, M., Calus, M. P. L., Megens, H.-J., Vereijken, A., Groenen, M. A. M., and Bastiaansen, J. W. M. (2016). Accuracy of genomic prediction using imputed whole-genome sequence data in white layers. J. Anim. Breed. Genet. 133, 167–179. doi: 10.1111/jbg.12199
Henshaw, J. M., Morrissey, M. B., and Jones, A. G. (2020). Quantifying the causal pathways contributing to natural selection. Evolution 74, 2560–2574. doi: 10.1111/evo.14091
Heslot, N., Akdemir, D., Sorrells, M. E., and Jannink, J.-L. (2014). Integrating environmental covariates and crop modeling into the genomic selection framework to predict genotype by environment interactions. TAG Theor. Appl. Genet. Theor. Angew. Genet. 127, 463–480. doi: 10.1007/s00122-013-2231-5
Hill, W. G. (2017). “““““Conversion””””” of epistatic into additive genetic variance in finite populations and possible impact on long-term selection response. J. Anim. Breed. Genet. 134, 196–201. doi: 10.1111/jbg.12270
Hill, W. G., Goddard, M. E., and Visscher, P. M. (2008). Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet 4:e1000008. doi: 10.1371/journal.pgen.1000008
Holzworth, D. P., Huth, N. I., deVoil, P. G., Zurcher, E. J., Herrmann, N. I., McLean, G., et al. (2014). apsimevolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 62, 327–350. doi: 10.1016/j.envsoft.2014.07.009
Houle, D., Govindaraju, D. R., and Omholt, S. (2010). Phenomics: the next challenge. Nat. Rev. Genet. 11, 855–866. doi: 10.1038/nrg2897
Huang, W., and Mackay, T. F. C. (2016). The genetic architecture of quantitative traits cannot be inferred from variance component analysis. bioRxiv[preprint] doi: 10.1101/041434 bioRxiv, 041434,
Janeiro, M. J., Henshaw, J. M., Pemberton, J. M., Pilkington, J. G., and Morrissey, M. B. (2020). Selection of lamb size and early pregnancy in Soay sheep (Ovies aries). bioRxiv [preprint] doi: 10.1101/2020.09.16.299685
Jarquín, D., Crossa, J., Lacaze, X., Cheyron, P. D., Daucourt, J., Lorgeou, J., et al. (2014). A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor. Appl. Genet. 127, 595–607. doi: 10.1007/s00122-013-2243-1
Jarquin, D., de Leon, N., Romay, C., Bohn, M., Buckler, E. S., Ciampitti, I., et al. (2021). Utility of climatic information via combining ability models to improve genomic prediction for yield within the genomes to fields maize project. Front. Genet. 11:592769. doi: 10.3389/fgene.2020.592769
Jones, J. W., Hoogenboom, G., Porter, C. H., Boote, K. J., Batchelor, W. D., Hunt, L. A., et al. (2003). The DSSAT cropping system model. Eur. J. Agron. 18, 235–265. doi: 10.1016/S1161-0301(02)00107-7
Jordan, D. R., Mace, E. S., Cruickshank, A. W., Hunt, C. H., and Henzell, R. G. (2011). Exploring and exploiting genetic variation from unadapted sorghum germplasm in a breeding program. Crop Sci. 51, 1444–1457. doi: 10.2135/cropsci2010.06.0326
Kruijer, W., Behrouzi, P., Bustos-Korts, D., Rodríguez-Álvarez, M. X., Mahmoudi, S. M., Yandell, B., et al. (2020). Reconstruction of networks with direct and indirect genetic effects. Genetics 214, 781–807. doi: 10.1534/genetics.119.302949
Lamkey, K. R. (1992). Fifty years of recurrent selection in the Iowa stiff stalk synthetic maize population. Maydica 37, 19–28.
Lamsal, A., Welch, S. M., White, J. W., Thorp, K. R., and Bello, N. M. (2018). Estimating parametric phenotypes that determine anthesis date in Zea mays: Challenges in combining ecophysiological models with genetics. PLoS One 13:e0195841. doi: 10.1371/journal.pone.0195841
Lande, R., and Arnold, S. J. (1983). The measurement of selection on correlated characters. Evolution 37:1210. doi: 10.2307/2408842
Legarra, A., Garcia-Baccino, C. A., Wientjes, Y. C. J., and Vitezica, Z. G. (2020). The correlation of substitution effects across populations and generations in the presence of non-additive functional gene action. bioArxiv. doi: 10.1101/2020.11.03.367227
Lewontin, R. C. (1974). The Genetic Basis of Evolutionary Change. New York, NY: Columbia University Press.
Liu, X., Li, Y. I., and Pritchard, J. K. (2019). Trans effects on gene expression can drive omnigenic inheritance. Cell 177, 1022–1034e6. doi: 10.1016/j.cell.2019.04.014
Mace, E. S., Cruickshank, A. W., Tao, Y., Hunt, C. H., and Jordan, D. R. (2020). A global resource for exploring and exploiting genetic variation in sorghum crop wild relatives. Crop Sci. 61, 150–162. doi: 10.1002/csc2.20332
Mace, E. S., Tai, S., Gilding, E. K., Li, Y., Prentis, P. J., Bian, L., et al. (2013). Whole-genome sequencing reveals untapped genetic potential in ‘ ‘Africa’s indigenous cereal crop sorghum. Nat. Commun. 4:2320. doi: 10.1038/ncomms3320
Mackay, I., Horwell, A., Garner, J., White, J., McKee, J., and Philpott, H. (2011). Reanalyses of the historical series of UK variety trials to quantify the contributions of genetic and environmental factors to trends and variability in yield over time. Theor. Appl. Genet. 122, 225–238. doi: 10.1007/s00122-010-1438-y
Mäki-Tanila, A., and Hill, W. G. (2014). Influence of gene interaction on complex trait variation with multilocus models. Genetics 198, 355–367. doi: 10.1534/genetics.114.165282
Malosetti, M., Ribaut, J.-M., and van Eeuwijk, F. A. (2013). The statistical analysis of multi-environment data: modeling genotype-by-environment interaction and its genetic basis. Front. Physiol. 4:44. doi: 10.3389/fphys.2013.00044
Marjoram, P., Zubair, A., and Nuzhdin, S. V. (2014). Post-GWAS: where next? More samples, more SNPs or more biology? Heredity 112, 79–88. doi: 10.1038/hdy.2013.52
Melchinger, A. E., and Gumber, R. K. (1998). Overview of heterosis and heterotic groups in agronomic crops. Concepts Breed. Heterosis Crop Plants 25, 29–44. doi: 10.2135/cssaspecpub25.c3
Messina, C. D., Cooper, M., Hammer, G. L., Berning, D., Ciampitti, I., Clark, R., et al. (2020). Two decades of creating drought tolerant maize and underpinning prediction technologies in the US corn-belt: review and perspectives on the future of crop design. [preprint] doi: 10.1101/2020.10.29.361337
Messina, C. D., Podlich, D., Dong, Z., Samples, M., and Cooper, M. (2011). Yield–trait performance landscapes: from theory to application in breeding maize for drought tolerance. J. Exp. Bot. 62, 855–868. doi: 10.1093/jxb/erq329
Meuwissen, T. H. E., Hayes, B. J., and Goddard, M. E. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.
Millet, E. J., Kruijer, W., Coupel-Ledru, A., Alvarez Prado, S., Cabrera-Bosquet, L., Lacube, S., et al. (2019). Genomic prediction of maize yield across European environmental conditions. Nat. Genet. 51, 952–956. doi: 10.1038/s41588-019-0414-y
Momen, M., Ayatollahi Mehrgardi, A., Amiri Roudbar, M., Kranis, A., Mercuri Pinto, R., Morota, G., et al. (2018). Including phenotypic causal networks in genome-wide association studies using mixed effects structural equation models. Front. Genet. 9:455. doi: 10.3389/fgene.2018.00455
Montesinos-López, O. A., Montesinos-López, A., Tuberosa, R., Maccaferri, M., Sciara, G., and Ammar, K. (2019). Multi-trait, multi-environment genomic prediction of durum wheat with genomic best linear unbiased predictor and deep learning methods. Front. Plant Sci. 10:1311. doi: 10.3389/fpls.2019.01311
Paixão, T., and Barton, N. H. (2016). The effect of gene interactions on the long-term response to selection. Proc. Natl. Acad. Sci. U.S.A. 113, 4422–4427. doi: 10.1073/pnas.1518830113
Pearl, J. (2012). The Causal Foundations of Structural Equation Modeling.Fort Belvoir, VA: Defense Technical Information Center, doi: 10.21236/ADA557445
Pegolo, S., Momen, M., Morota, G., Rosa, G. J. M., Gianola, D., Bittante, G., et al. (2020). Structural equation modeling for investigating multi-trait genetic architecture of udder health in dairy cattle. Sci. Rep. 10:7751. doi: 10.1038/s41598-020-64575-3
Piepho, H.-P. (1997). Analyzing genotype-environment data by mixed models with multiplicative terms. Biometrics 53, 761–766. doi: 10.2307/2533976
Podlich, D. W., Winkler, C. R., and Cooper, M. (2004). Mapping as you go: an effective approach for marker-assisted selection of complex traits. Crop Sci. 44, 1560–1571. doi: 10.2135/cropsci2004.1560
Powell, O., Gaynor, R. C., Gorjanc, G., Werner, C. R., and Hickey, J. M. (2020). A two-part strategy using genomic selection in hybrid crop breeding programs. bioArxiv doi: 10.1101/2020.05.24.113258
Pszczola, M., Strabel, T., Mulder, H. A., and Calus, M. P. L. (2012). Reliability of direct genomic values for animals with different relationships within and to the reference population. J. Dairy Sci. 95, 389–400. doi: 10.3168/jds.2011-4338
Puillet, L., Ducrocq, V., Friggens, N. C., and Amer, P. R. (2021). Exploring underlying drivers of genotype by environment interactions in feed efficiency traits for dairy cattle with a mechanistic model involving energy acquisition and allocation. J. Dairy Sci. 104, 5805–5816. doi: 10.3168/jds.2020-19610
Puillet, L., Réale, D., and Friggens, N. C. (2016). Disentangling the relative roles of resource acquisition and allocation on animal feed efficiency: insights from a dairy cow model. Genet. Sel. Evol. 48:72. doi: 10.1186/s12711-016-0251-8
Reeve, J. P. (2000). Predicting long-term response to selection. Genet. Res. 75, 83–94. doi: 10.1017/S0016672399004140
Rio, S., Mary-Huard, T., Moreau, L., Bauland, C., Palaffre, C., Madur, D., et al. (2020). Disentangling group specific QTL allele effects from genetic background epistasis using admixed individuals in GWAS: An application to maize flowering. PLoS Genet. 16:e1008241. doi: 10.1371/journal.pgen.1008241
Robert, P., Le Gouis, J., Consortium, T. B., and Rincent, R. (2020). Combining crop growth modeling with trait-assisted prediction improved the prediction of genotype by environment interactions. Front. Plant Sci. 11:827. doi: 10.3389/fpls.2020.00827
Robertson, A. (1959). The sampling variance of the genetic correlation coefficient. Biometrics 15:469. doi: 10.2307/2527750
Robertson, A. (1960). A theory of limits in artificial selection. Proc. R. Soc. Lond B 153, 234–249. doi: 10.1098/rspb.1960.0099
Tanksley, S. D., and McCouch, S. R. (1997). Seed banks and molecular maps: unlocking genetic potential from the wild. Science 277, 1063–1066. doi: 10.1126/science.277.5329.1063
Tardieu, F., Granato, I. S. C., Van Oosterom, E. J., Parent, B., and Hammer, G. L. (2020). Are crop and detailed physiological models equally “mechanistic’ for predicting the genetic variability of whole-plant behaviour? The nexus between mechanisms and adaptive strategies. Silico Plants 2:diaa011. doi: 10.1093/insilicoplants/diaa011
Technow, F., Messina, C. D., Totir, L. R., and Cooper, M. (2015). Integrating crop growth models with whole genome prediction through approximate bayesian computation. PLoS One 10:e0130855. doi: 10.1371/journal.pone.0130855
Technow, F., Podlich, D., and Cooper, M. (2020). Back to the future: implications of genetic complexity for hybrid breeding strategies. bioRxiv [preprint] doi: 10.1101/2020.10.21.349332 bioRxiv, 2020.10.21.349332,
Tiezzi, F., Valente, B. D., Cassandro, M., and Maltecca, C. (2015). Causal relationships between milk quality and coagulation properties in Italian Holstein-Friesian dairy cattle. Genet. Sel. Evol. 47:45. doi: 10.1186/s12711-015-0123-7
Toda, Y., Wakatsuki, H., Aoike, T., Kajiya-Kanegae, H., Yamasaki, M., Yoshioka, T., et al. (2020). Predicting biomass of rice with intermediate traits: modeling method combining crop growth models and genomic prediction models. PLoS One 15:e0233951. doi: 10.1371/journal.pone.0233951
Tsutsumi-Morita, Y., Heuvelink, E., Khaleghi, S., Bustos-Korts, D., Marcelis, L. F. M., Vermeer, K. M. C. A., et al. (2021). Yield dissection models to improve yield; a case study in tomato. Silico Plants 3:diab012. doi: 10.1093/insilicoplants/diab012
Valente, B. D., Rosa, G. J. M., de los Campos, G., Gianola, D., and Silva, M. A. (2010). Searching for recursive causal structures in multivariate quantitative genetics mixed models. Genetics 185, 633–644. doi: 10.1534/genetics.109.112979
Valente, B. D., Rosa, G. J. M., Gianola, D., Wu, X.-L., and Weigel, K. (2013). Is structural equation modeling advantageous for the genetic improvement of multiple traits? Genetics 194, 561–572. doi: 10.1534/genetics.113.151209
van Eeuwijk, F. A., Malosetti, M., Yin, X., Struik, P. C., and Stam, P. (2005). Statistical models for genotype by environment data: from conventional ANOVA models to eco-physiological QTL models. Aust. J. Agric. Res. 56, 883–894. doi: 10.1071/AR05153
Werner, C. R., Gaynor, R. C., Sargent, D. J., Lillo, A., Gorjanc, G., and Hickey, J. M. (2020). Genomic selection strategies for clonally propagated crops. bioArxiv doi: 10.1101/2020.06.15.152017
White, M. R., Mikel, M. A., de Leon, N., and Kaeppler, S. M. (2020). Diversity and heterotic patterns in North American proprietary dent maize germplasm. Crop Sci. 60, 100–114. doi: 10.1002/csc2.20050
Wientjes, Y., Veerkamp, R. F., Bijma, P., Bovenhuis, H., Schrooten, C., and Calus, M. (2015). Empirical and deterministic accuracies of across-population genomic prediction. Genet. Sel. Evol. 47:5. doi: 10.1186/s12711-014-0086-0
Wientjes, Y. C. J., Bijma, P., Calus, M. P. L., Zwaan, B. J., Vitezica, Z. G., and van den Heuvel, J. (2021). The long-term effects of genomic selection: Response to selection, additive genetic variance and genetic architecture. bioRxiv [preprint] doi: 10.1101/2021.03.16.435664 bioRxiv, 2021.03.16.435664,
Windhausen, V. S., Atlin, G. N., Hickey, J. M., Crossa, J., Jannink, J.-L., Sorrells, M. E., et al. (2012). Effectiveness of genomic prediction of maize hybrid performance in different breeding populations and environments. G3 Genes Genomes Genet. 2, 1427–1436. doi: 10.1534/g3.112.003699
Wright, S. (1963). ““““““Discussion: Plant and Animal Improvement in the Presence of Multiple Selective Peaks”””””,” in Statistical Genetics and Plant Breeding. Washington, D.C: National Academies Press, 116–122. doi: 10.17226/20264
Keywords: multi-trait prediction, non-linear relationships, crop growth models, genetic correlation, non-additive genetic effects, epistasis, pleiotropy, GxE interactions
Citation: Powell OM, Voss-Fels KP, Jordan DR, Hammer G and Cooper M (2021) Perspectives on Applications of Hierarchical Gene-To-Phenotype (G2P) Maps to Capture Non-stationary Effects of Alleles in Genomic Prediction. Front. Plant Sci. 12:663565. doi: 10.3389/fpls.2021.663565
Received: 03 February 2021; Accepted: 13 April 2021;
Published: 04 June 2021.
Edited by:
Johannes W.R. Martini, International Maize and Wheat Improvement Center, MexicoReviewed by:
Torsten Pook, University of Göttingen, GermanyDiercles Francisco Cardoso, São Paulo State University, Brazil
Kanwarpal Singh Dhugga, Consultative Group on International Agricultural Research (CGIAR), United States
Copyright © 2021 Powell, Voss-Fels, Jordan, Hammer and Cooper. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Owen M. Powell, by5wb3dlbGwyQHVxLmVkdS5hdQ==
 Owen M. Powell
Owen M. Powell Kai P. Voss-Fels
Kai P. Voss-Fels David R. Jordan
David R. Jordan Graeme Hammer
Graeme Hammer Mark Cooper
Mark Cooper