- Instituto de Investigaciones Biomédicas, Universidad Nacional Autónoma de México, Distrito Federal, México
There is a wealth of molecular information that has enhanced the reconstruction of regulatory networks and pathways in plants, specially in Arabidopsis thaliana due to its central role as a model system. Most of this information, however, has proven to be insufficient to construct quantitative models due to the absence of sufficiently accurate measurements of kinetic constants. Hence, there have been efforts to develop qualitative methodologies that permit the use of the vast information regarding the regulatory interactions among molecules.
Of special interest is the increasing use of Boolean models to analyze the dynamic behavior of regulatory networks (Bornholdt, 2008), with an emphasis in the description of the steady states of activation, as well as the characterization of their basins of attraction. The accuracy of these models at describing the experimentally observed set of molecular markers characteristic of observed cell types is the central argument to validate the use of a Boolean approach. These discrete-state models are thereafter used to make specific predictions about the dynamical behavior of the network and about missing links or nodes in its topology.
The methodology known as standardized qualitative dynamical systems, SQUAD (http://www.enfin.org/Wiki/SQUAD/about-squad; Mendoza and Xenarios, 2006; Di Cara et al., 2007), was developed to create a continuous dynamical system with a set of differential equations of a regulatory network using exclusively topological information. This was possible by devising a set of ordinary differential equations with properties similar to a Boolean system. Such characteristic has two main advantages; first, the user does not need to provide any kind of kinetic parameters; and second, the methodology provides a way to make a fully automated analysis of the dynamical behavior of the model. As a result, the original version of the methodology makes it suitable to obtain a continuous qualitative model of a given network. For example, the SQUAD methodology has been used to study the auxin and brassinosteroid pathways in A. thaliana (Sankar et al., 2011). This methodology allowed the analysis of several models with varying network topologies, thus explaining the effect of certain mutations. Importantly, the model permitted the generation of a prediction regarding a regulatory interaction that was confirmed experimentally (Scacchi et al., 2010).
Despite its advantages, the SQUAD method as described in its original form does not allow the user to specify the logical rules for each node. The algorithm assumes that any positive regulator is strong enough to activate its target in the absence of an inhibitor. Also, it assumes that any negative regulator is stronger that any combination of positive regulators. These two assumptions are not necessarily true for a particular network. Indeed, the flower organ specification gene regulatory network of xtit A. thaliana does not conform to the previous assumptions, and therefore it was necessary to modify the SQUAD methodology so as to permit the use of arbitrary regulatory rules in a network (Sánchez-Corrales et al., 2010). This modification is important since it provides the modelers with a way to incorporate relevant experimental data into the model. At the same time, the incorporation of specific logical rules for each node in a network makes the new version of SQUAD a methodology that requires the use of more information than the sole topology of the network.
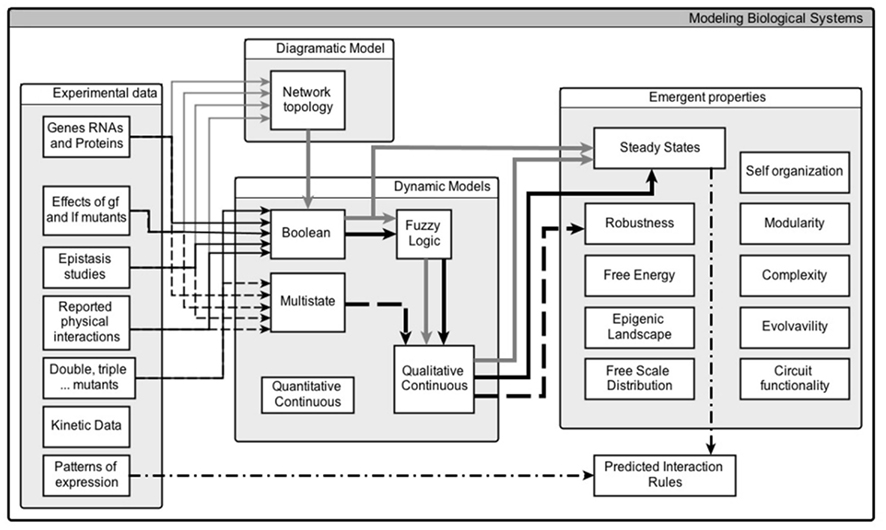
Figure 1 shows the general characteristics of the first and second versions of SQUAD, as well as some of its possible developments. In the original version, indicated by the flux of information with gray arrows, the methodology accepts as input the topology of the network, which includes the nodes, as well as their signed interactions. With such information, the algorithm creates a set of Boolean rules with the two assumptions described in the previous paragraph. Then, the steady states of the Boolean model are found with the use of binary decision diagrams (Garg et al., 2007), which are representations of Boolean functions in the form of graphs. Next, a continuous dynamical system with the form of a set of ordinary differential equations is created with predefined sigmoid functions. And finally, the set of equations is solved numerically using as initial conditions the steady states recovered from the Boolean model.
The second version of SQUAD, where the Boolean rules can be customized, is shown in Figure 1 with the flux of information as thin black arrows. In this case, the user specifies the Boolean actualization rules, usually because there is enough experimental information showing the inadequacy of the assumptions of the original version of SQUAD. Then, the Boolean rules are transformed into their continuous equivalents with the use of fuzzy logic, which is an extension of two-valued logic such that statements need not be true or false, but may have a degree of truth between 0 and 1. Such rules are then inserted into a predefined skeleton of a system of ordinary differential equations, and the resulting system is numerically integrated using a large set of random initial states (thick black arrows).
We hereby propose further modifications to the SQUAD methodology, so as to make it more flexible, and therefore more amply used for qualitative modeling. First, it would be valuable to incorporate a defined level of noise to the numerical solutions, shown as thick broken arrows in Figure 1. In this way, it would be possible to incorporate the stochastic effects observed in experimental settings due to variations in the concentration of molecules, as well as due to uncontrolled variables. Also, we think that it would be beneficial to reimplement SQUAD as a software package from scratch, with code optimization in mind, thus making it suitable for simulating large regulatory networks. Moreover, a future version of SQUAD may be benefited by the incorporation of logical actualization rules with multiple thresholds, shown as thin broken arrows in Figure 1. Some regulatory networks need to be modeled with multiple levels of activation for some nodes (see for example Mendoza, 2006), and thus it would be desirable to extend the methodology to create a set of ordinary differential equations based on a multivalued discrete model. Finally, it would be very useful to incorporate the capability on the program to suggest new interactions or logical rules, indicated with thin dotted broken arrows in Figure 1, which might fit a regulatory network to a set of target expected attractors, obtained from experimentally observed stable patterns of expression.
Of special interest to us at the present time is the incorporation of multiple states of activation into a regulatory network. If a multivalued discrete system is going to be transformed into a set of differential equations, it would be important for the continuous system to preserve the attractors obtained from a multivalued discrete system. Transforming multivalued logic update rules into their continuous fuzzy logic counterparts is not straightforward, but one possible implementation worth exploring is describing the rate of change of activation of a node with the use of the following equation:
Where Xi is the activation state of node i. 0 < ki < = 1 is a constant that controls how fast the state of the node Xi changes. Finally, Ui is the state the node i would reach if the conditions remain as they are now; in other words, it is the value returned by the update rule of the multivalued discrete model.
Now, given that noise is a very important factor in the dynamical behavior of biological systems, and that most systems resist a certain amount of noise while others require noise to function correctly (Eldar and Elowitz, 2010), the previous equation may be extended to add noise:
Where z is a positive real constant that defines the noise level, and rnd is a random number generator that returns a value in the interval [−1, 1].
Due to the large diversity of biological systems, modeling methods must be tailored to make the best use of the available experimental information, as well as to answer specific biological questions, which can span from the understanding of the function of a pathway and its evolution to the global molecular mechanisms underlying cellular events such as cell differentiation. One of these modeling methods, SQUAD, is in its present form a straightforward tool that has been applied mainly for the qualitative modeling of regulatory networks of plants (Sánchez-Corrales et al., 2010; Sankar et al., 2011). These models show that there is a correspondence in the number and location of stable steady states found by SQUAD and classic Boolean modeling. However, due to its formulation as a set of ordinary differential equations, SQUAD may find additional unstable steady states, cyclic behavior, and different attractor basin sizes with respect to Boolean approaches. These differences have allowed SQUAD to be a tool suitable to study the effect of extracellular signals on the determination in the order of attractors reached during a differentiation process (see for example Mendoza and Pardo, 2010; Sánchez-Corrales et al., 2010).
Despite its usefulness, it is clear that there is ample room for refinement and generalization of the SQUAD method. We hereby sketched some of the possible ways in which the modeling methodology may be extended, and thus broaden its range of applications. Nonetheless, SQUAD in its present form complements other packages or platforms like Antelope (Arellano et al., 2011), BoolNet (Müssel et al., 2010), and GINsim (Chaouiya et al., 2012), to analyze dynamics (Machado et al., 2011), robustness (Kitano, 2004), modularity (Ravasz et al., 2002), and evolvability (Mugler et al., 2009), among other network properties.
References
Arellano, G., Argil, J., Azpeitia, E., Benitez, M., Carrillo, M., Gongora, P., Rosenblueth, D. A., and Alvarez-Buylla, E. R. (2011). “Antelope”: a hybrid-logic model checker for branching-time Boolean GRN analysis. BMC Bioinformatics 12, 490. doi:10.1186/1471-2105-12-490
Bornholdt, S. (2008). Boolean network models of cellular regulation: prospects and limitations. J. R. Soc. Interface 5, S85–S94.
Chaouiya, C., Naldi, A., and Thieffry, D. (2012). Logical modelling of gene regulatory networks with GINsim. Methods Mol. Biol. 804, 463–479.
Di Cara, A., Garg, A., De Micheli, G., Xenarios, I., and Mendoza, L. (2007). Dynamic simulation of regulatory networks using SQUAD. BMC Bioinformatics 8, 462. doi: 10.1186/1471-2105-8-462
Eldar, A., and Elowitz, M. B. (2010). Functional roles for noise in genetic circuits. Nature 467, 167–173.
Garg, A., Xenarios, I., Mendoza, L., and DeMicheli, G. (2007). Efficient methods for dynamic analysis of genetic networks and in silico gene perturbation experiments. Lect. Notes Comput. Sci. 4453, 62–76.
Machado, D., Costa, R. S., Rocha, M., Ferreira, E. C., Tidor, B., and Rocha, I. (2011). Modeling formalisms in systems biology. AMB Express 1, 45.
Mendoza, L. (2006). A network model for the control of the differentiation process in Th cells. Biosystems 84, 101–114.
Mendoza, L., and Pardo, F. (2010). A robust model to describe the differentiation of T-helper cells. Theory Biosci. 129, 283–293.
Mendoza, L., and Xenarios, I. (2006). A method for the generation of standardized qualitative dynamical systems of regulatory networks. Theor. Biol. Med. Model. 3, 13.
Mugler, A., Ziv, E., Nemenman, I., and Wiggins, C. H. (2009). Quantifying evolvability in small biological networks. IET Syst. Biol. 3, 379–387.
Müssel, C., Hopfensitz, M., and Kestler, H. A. (2010). BoolNet-an R package for generation, reconstruction and analysis of Boolean networks. Bioinformatics 26, 1378–1380.
Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z. N., and Barabasi, A. L. (2002). Hierarchical organization of modularity in metabolic networks. Science 297, 1551–1555.
Sánchez-Corrales, Y. E., Alvarez-Buylla, E. R., and Mendoza, L. (2010). The Arabidopsis thaliana flower organ specification gene regulatory network determines a robust differentiation process. J. Theor. Biol. 264, 971–983.
Sankar, M., Osmont, K. S., Rolcik, J., Gujas, B., Tarkowska, D., Strnad, M., Xenarios, I., and Hardtke, C. S. (2011). A qualitative continuous model of cellular auxin and brassinosteroid signaling and their crosstalk. Bioinformatics 27, 1404–1412.
Citation: Weinstein N and Mendoza L (2012) Building qualitative models of plant regulatory networks with SQUAD. Front. Plant Sci. 3:72. doi: 10.3389/fpls.2012.00072
Received: 07 March 2012; Accepted: 28 March 2012;
Published online: 19 April 2012.
Copyright: © 2012 Weinstein and Mendoza. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence:bG1lbmRvemFAYmlvbWVkaWNhcy51bmFtLm14