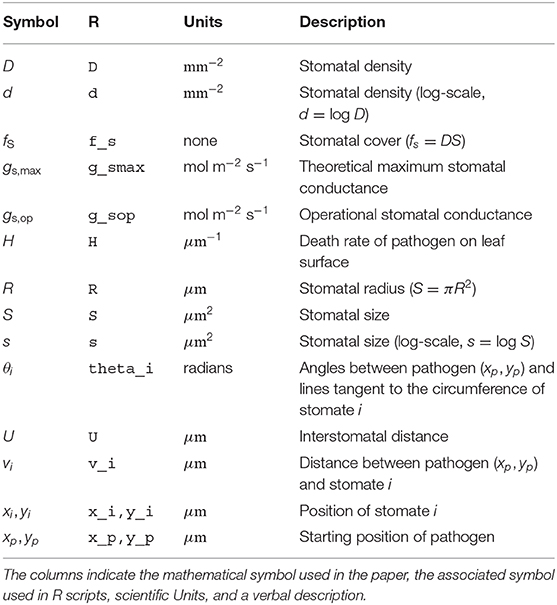
- School of Life Sciences, University of Hawai'i, Honolulu, HI, United States
Stomatal pores control leaf gas exchange and are one route for infection of internal plant tissues by many foliar pathogens, setting up the potential for tradeoffs between photosynthesis and pathogen colonization. Anatomical shifts to lower stomatal density and/or size may also limit pathogen colonization, but such developmental changes could permanently reduce the gas exchange capacity for the life of the leaf. I developed and analyzed a spatially explicit model of pathogen colonization on the leaf as a function of stomatal size and density, anatomical traits which partially determine maximum rates of gas exchange. The model predicts greater stomatal size or density increases the probability of colonization, but the effect is most pronounced when the fraction of leaf surface covered by stomata is low. I also derived scaling relationships between stomatal size and density that preserves a given probability of colonization. These scaling relationships set up a potential anatomical conflict between limiting pathogen colonization and minimizing the fraction of leaf surface covered by stomata. Although a connection between gas exchange and pathogen defense has been suggested empirically, this is the first mathematical model connecting gas exchange and pathogen defense via stomatal anatomy. A limitation of the model is that it does not include variation in innate immunity and stomatal closure in response to pathogens. Nevertheless, the model makes predictions that can be tested with experiments and may explain variation in stomatal size and density among plants. The model is generalizable to many types of pathogens, but lacks significant biological realism that may be needed for precise predictions.
Introduction
Stomata evolved to regulate gas exchange in and out of the leaf (Hetherington and Woodward, 2003; Berry et al., 2010; Chater et al., 2017), but many foliar pathogens take advantage of these chinks in the leaf cuticular armor to infect prospective hosts (Zeng et al., 2010; McLachlan et al., 2014; Melotto et al., 2017). The stomatal and mesophyll conductance to CO2 are two major limits to photosynthesis (Flexas et al., 2018; Lawson et al., 2018) that are partially determined by stomatal anatomy. Since CO2 conductance limits photosynthesis (Farquhar and Sharkey, 1982; Jones, 1985) and pathogen infection can reduce fitness (Gilbert, 2002), this sets up a potential tradeoff between increased photosynthesis and defense against pathogens mediated by stomatal anatomy (McKown et al., 2014; Dutton et al., 2019; Fetter et al., 2019; Tateda et al., 2019). For example, plants could increase photosynthetic rate by developing more stomata, but more stomata could result in more pathogen colonization. The optimal stomatal density, size, and arrangement on the leaf will depend on the fitness gains from increased gas exchange and fitness losses imposed by foliar pathogens, both of which depend on the environment. In the next two paragraphs I will review the relationship between stomatal anatomy, gas exchange, and foliar pathogen colonization. Then I will discuss why two anatomical traits, stomatal size and density, might be crucial components of a broader tradeoff between photosynthesis and pathogen defense.
The stomatal density and maximum pore area set an anatomical upper limit on stomatal conductance (Brown and Escombe, 1900; Parlange and Waggoner, 1970; Franks and Farquhar, 2001; Franks and Beerling, 2009b; Lehmann and Or, 2015; Sack and Buckley, 2016; Harrison et al., 2019), but stomatal shape, distribution, and patterning also affect gas exchange. Smaller guard cells and dumbbell-shaped stomata of grasses can respond faster to environmental changes (Drake et al., 2013), but responsiveness is further modulated by subsidiary cell anatomy and physiology (Franks and Farquhar, 2007; Raissig et al., 2017; Gray et al., 2020). Stomatal clustering reduces gas exchange and photosynthesis because adjacent stomata interfere with one another (Dow et al., 2014b), diffusion shells overlap (Lehmann and Or, 2015), and limitations on lateral diffusion of CO2 in the mesophyll (Lawson and Blatt, 2014 and references therein). However, sparse clusters of small stomata could allow a leaf with low rates of gas exchange to have faster stomatal response compared to a leaf with large, low-density stomata (Papanatsiou et al., 2017). Leaves with stomata on both lower and upper surfaces (amphistomatous) supply more CO2 to the mesophyll than hypostomatous leaves that only have stomata on the lower surface (Parkhurst, 1978; Gutschick, 1984; Parkhurst and Mott, 1990; Oguchi et al., 2018). In addition to anatomy, the pore area shrinks and expands in response to internal and external factors to regulate gas exchange dynamically (Buckley, 2019). For example, stomata typically open during the day and close at night in C3/C4 plants, but the opposite is true for CAM plants. Shade, high vapor pressure deficits, dry soil and other factors can cause stomata to (partially) close even in the middle of the day. Variation in how stomata respond to internal and external signals may explain as much of the variation in gas exchange across leaves as anatomy (Lawson and Blatt, 2014).
Many types of foliar pathogens, including viruses (Murray et al., 2016), bacteria (Melotto et al., 2006; Underwood et al., 2007), protists (Fawke et al., 2015), and fungi (Hoch et al., 1987; Zeng et al., 2010) use stomatal pores to gain entry into the leaf. For example, rust fungi hyphae recognize the angle at which guard cells project from the leaf surface and use it as a cue for appressorium formation (Allen et al., 1991). Oomycete pathogens can target open stomata on a leaf (Kiefer et al., 2002). Plants can limit colonization through innate immunity, called stomatal defense (recently reviewed in Melotto et al., 2017), by closing stomata after they recognize microbe-associated molecular patterns (MAMPs) on pathogen cells. Some bacterial pathogens have responded by evolving the ability to prevent stomatal closure, increasing their colonization of the leaf interior (Melotto et al., 2006). In addition to stomatal closure, anatomical changes in stomatal density and/or size might provide another layer of defense against pathogen colonization. For example, infection increases in leaves with higher stomatal density (McKown et al., 2014; Dutton et al., 2019; Fetter et al., 2019; Tateda et al., 2019). The positive effect of stomatal density on infection suggests that infection is limited by the number or size of locations for colonization, meaning that many individual pathogens must usually be unable to find stomata or other suitable locations for colonization. This is actually somewhat surprising given the ability of some pathogens to search for and sense stomata (see above).
Stomatal anatomy could be a key link between gas exchange and pathogen colonization. Although many anatomical factors and stomatal movement affect gas exchange (see above), here I focus on the density and size of stomata in a hypostomatous leaf. Stomatal size refers to both the area of guard cells when fully open, from which one can calculate the pore area for gas exchange (see Model). For simplicity, I model a hypostomatous leaf, but consider the implications for amphistomatous leaves in the Discussion. Stomatal size and density not only determine the theoretical maximum stomatal conductance (gs,max), but are also proportional to the operational stomatal conductance (gs,op) in many circumstances (Franks et al., 2009, 2014; Dow et al., 2014a; McElwain et al., 2016; Murray et al., 2019). gs,op is the actual stomatal conductance of plants in the field and is almost always below gs,max because stomata are usually not fully open. Although they are not the same, the strong empirical relationship between gs,max and gs,op means that anatomical gs,max can be used as a proxy for gs,op without explicitly modeling dynamic changes in stomatal aperture (see Discussion). Stomatal size and density have also been measured on many more species than stomatal responsiveness, which may make it easier to test predictions.
After a pathogen reaches a host, it must survive on the leaf surface and colonize the interior (Beattie and Lindow, 1995; Tucker and Talbot, 2001). For analytical tractability, I restrict the focus here to colonization by a pathogen using a random search on a leaf without stomatal defense (i.e., a leaf that cannot recognize pathogens and close stomata). Obviously, these simplifications ignore a lot of important plant-pathogen interaction biology. In the Discussion, I delve further into these limitations and suggest future work to overcome these limitations. In order for pathogen-mediated selection on stomatal anatomy, I assume that the pathogen reduces host fitness once it colonizes (Gilbert, 2002). Susceptible hosts can lose much of their biomass or die, but even resistant hosts must allocate resources to defense or reduce photosynthesis because of defoliation, biotrophy, or necrosis around sites of infection (Bastiaans, 1991; Mitchell, 2003).
The purpose of this study is to develop a theoretical framework to test whether variation in stomatal size and density arises from a tradeoff between gas exchange and pathogen colonization. Since stomatal size and density affect both gas exchange and pathogen colonization, selection to balance these competing demands could shape stomatal size-density scaling relationships. Botanists have long recognized that stomatal size and density are inversely correlated (Weiss, 1865; Tichá, 1982; Hetherington and Woodward, 2003; Sack et al., 2003; Franks and Beerling, 2009a; Brodribb et al., 2013; Boer et al., 2016), but the evolutionary origin of this relationship is not yet known. Here I argue that deleterious effects of pathogen infection could shape selection on this relationship. Explanations for inverse size-density scaling are usually cast in terms of preserving gs,max and/or stomatal cover (fS), defined at the fraction of epidermal area allocated to stomata (Boer et al., 2016), because there are many combinations of stomatal size and density that have same gs,max or same fS:
D and S are stomatal density and size, respectively (see Table 1 for a glossary of mathematical symbols and units). b and m are assumed to be biophysical and morphological constants, sensu (Sack and Buckley, 2016; see Supplementary Material). fS is proportional to the more widely used stomatal pore area index (Sack et al., 2003; see Supplementary Material). If size and density also affect pathogen colonization, then selection from foliar pathogens could significantly alter the size-density scaling relationship. The empirical size-density scaling relationship is linear on a log-log scale, determined by an intercept α and slope β:
For brevity, d = log(D) and s = log(S). Rearranging Equations 1 and 2, a scaling relationship where β = 0.5 preserves gs,max while β = 1 preserves fS.
How would adding pathogens alter these predicted scaling relationships? For simplicity, consider two environments, one without foliar pathogens and one with lots. In the absence of foliar pathogens, we expect size-density scaling to preserve gs,max, fS, or some least-cost combination of them. What happens when we introduce pathogens? If stomatal size and density increase pathogen colonization, then selection will favor reduced size and/or density. This would change the intercept α but not the slope. The effect of foliar pathogens on the slope depends on the relationship between size, density, and probability of colonization. If the probability of colonization is proportional to the product of linear stomatal size (S0.5) and density (∝ DS0.5 as for gs,max) then it has the same effect on the slope as gs,max because there are many combinations of D and S0.5 that have same probability of colonization. If the probability of colonization is proportional to the product of areal stomatal size (S) and density (∝ DS as for fS) then it has the same effect on the slope as fS because there are many combinations of D and S that have same probability of colonization. Alternatively, the probability of colonization may have a different scaling relationship (neither 0.5 nor 1) or may be non-linear on a log-log scale. Unlike gs,max and fS, we do not have theory to predict a stomatal size-density relationship that preserves the probability of colonization.
In summary, the physical relationship between stomatal size, density, and conductance is well-established (Harrison et al., 2019). Size and density also likely affect the probability of pathogen colonization, but we do not have a theoretical model that makes quantitative predictions. The inverse stomatal size-density relationship has usually been explained in terms of preserving stomatal conductance and/or stomatal cover, but selection by pathogens might alter scaling. To address these gaps, the goals of this study are to (1) introduce a spatially explicit model pathogen colonization on the leaf surface; (2) use the model to predict the relationship between gs,max, fS, and the probability of colonization; (3) work out what these relationships predict about stomatal size-density scaling. I analyzed an idealized, spatially explicit Model of how a pathogen lands on a leaf and finds a stomate to colonize the leaf using a random search. To my knowledge, this is the first model that makes quantitative predictions about the relationship between stomatal anatomy, the probability of colonization, and their impact on stomatal size-density scaling.
Model
For generality, I refer to a generic “pathogen” that lands on leaf and moves to a stomate. The model is agnostic to the type of pathogen (virus, bacterium, fungus, etc.) and the specific biological details of how it moves. For example, motile bacterial cells can land and move around (Beattie and Lindow, 1995) whereas fungi may germinate from a cyst and grow until they form an appresorium for infection (Tucker and Talbot, 2001). These very different tropic movements on the leaf are treated identically here. I do not model photosynthesis explicitly, but assume that stomatal conductance limits carbon fixation, even though the relationship is non-linear. I used Sympy version 1.6.1 (Meurer et al., 2017) for symbolic derivations.
Spatial Representation of Stomata
Stomata develop relatively equal spacing to minimize resistance to lateral diffusion (Morison et al., 2005), allow space between stomata (Dow et al., 2014b), and prevent stomatal interference (Lehmann and Or, 2015). Here I assume that stomata are arrayed in an equilateral triangular grid with a density D and size (area) S on the abaxial surface only, since most leaves are hypostomatous (Muir, 2015; but see Discussion). This assumption ignores veins, trichomes, and within-leaf variation in stomatal density. Stomata are therefore arrayed in an evenly spaced grid (Figure 1A). The interstomatal distance U, measured as the distance from the center of one stomata to the next, is the maximal diagonal of the hexagon in μm that forms an equal area boundary between neighboring stomata. The area of a hexagon is . By definition the stomatal density is the inverse of this area, such that . Therefore, interstomatal distance can be derived from the stomatal density as:
For example, if the density is D = 102 mm−2 = 10−4 μm−2, then U is 107.5 μm. Parkhurst (1994) described this result previously. I also make the simplifying assumption that stomata are perfectly circular with radius R when fully open. This may be approximately true for fully open stomata with kidney-shaped guard cells (Sack and Buckley, 2016 and references therein). Although I assume stomata are circular here, in calculating gs,max, I assume typical allometric relationships between length, width, and pore area (Sack and Buckley, 2016; see Supplementary Material).
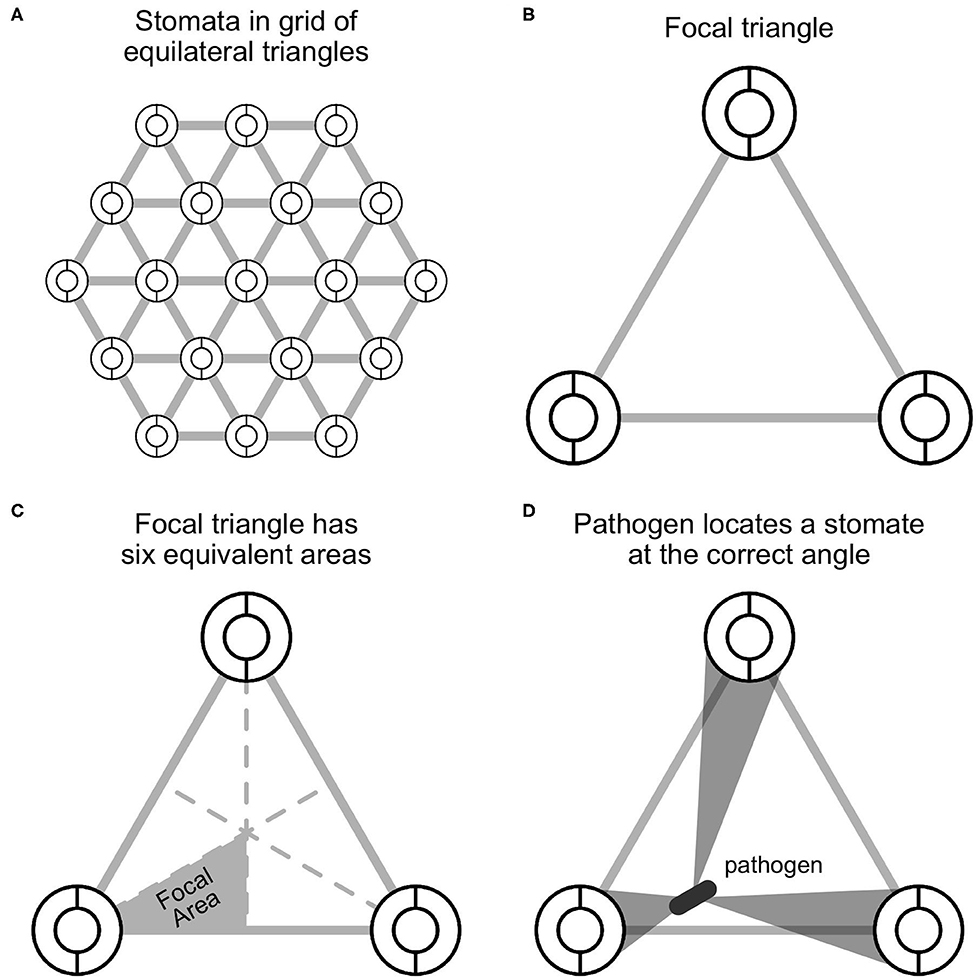
Figure 1. A spatially explicit model of stomatal anatomy and pathogen colonization. (A) Stomata are assumed to be in a homogenous equilateral triangular grid, which means that we can extrapolate from (B) a focal triangle to the entire leaf. The circles represent idealized stomata; the gray lines between them are for visualization. (C) By symmetry, a single focal region within the focal triangle can be modeled and extrapolated to the rest of the triangle. (D) The model assumes that a pathogen, depicted as a gray rod, lands somewhere on the leaf surface and will successfully locate a stomate if it moves at the correct angle, depicted by the gray polygons.
Spatial Representation of Pathogen Search
Since stomata are arrayed in a homogeneous grid, we can focus on single focal triangle (Figures 1B,C). Suppose that an individual pathogen (e.g., bacterial cell or fungal spore) lands at a uniform random position within the focal triangle and must arrive at a stomate to colonize. If it lands on a stomate, then it infects the leaf with probability 1; if it lands between stomata, then it infects the leaf with probability plocate. This is the probability that it locates a stomate, which I will derive below. The probabilities of landing on or between a stomate are fS and 1−fS, respectively. Hence, the total probability of colonization is:
I assume that the pathogen cannot sense where stomata are and orients at random, thereafter traveling in that direction. If it successfully locates a stomate, it colonizes the leaf, but otherwise does not infect. If there is a high density of stomata and/or large stomata, the probability of locating a stomate increases. By assuming that stomata form an equilateral triangular grid (see above), we can extrapolate what happens in the focal triangle (Figure 1B) by symmetry. Further, since an equilateral triangle can be broken up into six identical units (Figure 1C), we can simply calculate plocate in this focal area. This implicitly assumes that the probability of colonizing stomata outside the focal area is 0 because they are too far away. This assumption may be unrealistic for larger pathogens, such as fungi, whose hyphae can travel longer distances on the leaf surface (Brand and Gow, 2012). In Appendix 1: Spatially Implicit Model I derive a simpler, but spatially implicit model that relaxes the assumption the pathogens must colonize a stomate within their focal triangle.
Consider a pathogen that lands in position (xp, yp) within the triangle. The centroid of the triangle is at position (xc, yc) and a reference stomate is at position (0, 0) (Figure 2A). Therefore xc = U/2 and . The other stomata are at positions and (U, 0) (Figure 2). xp and yp are defined as the horizontal and vertical distances, respectively, from the pathogen to the reference stomate at position (0, 0).
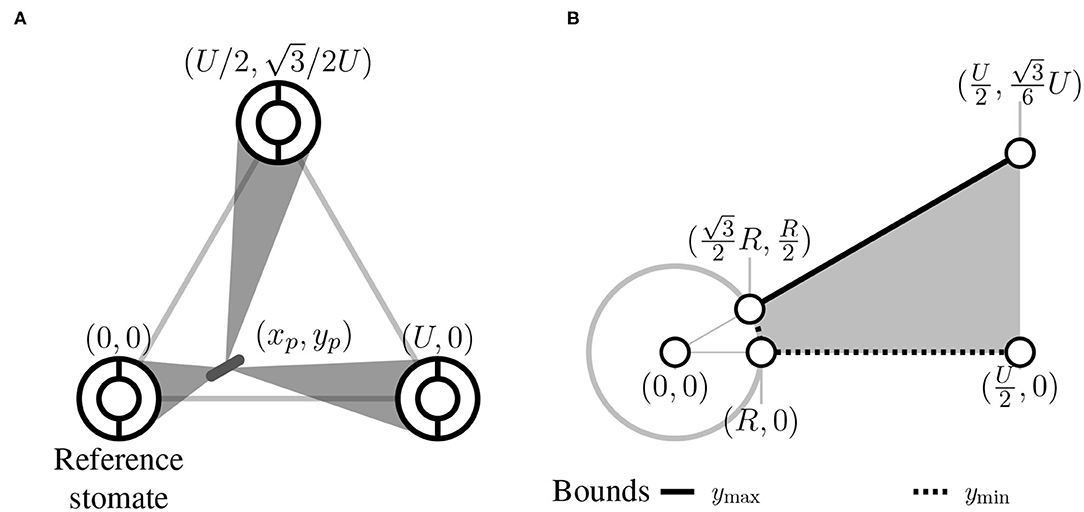
Figure 2. Spatial representation of stomata and pathogen. (A) The pathogen starts at a uniform random position within the focal region denoted (xp, yp). Within the focal triangle, the reference stomate is at position (0,0) by definition, and other stomatal positions are determined by the interstomatal distance U. (B) Within the focal region, a pathogen can land within the stomate (white circle with gray outline and radius R) or in the gray area. The outer borders of this area are shown and depend on R and U. For a given position x, there is a minimum y-value (ymin, dashed line) and maximum y-value (ymax, solid line).
Given that the pathogen starts at position (xp, yp), what's the probability of contacting one of the stomata at the vertices of the focal triangle? I assume the probability of contacting a stomate is equal to the proportion of angular directions that lead to a stomate (Figure 1D). I solved this by finding the angles (θ1, θ2, θ3) between lines that are tangent to the outside of the three stomata and pass through (xp, yp) (Figure 2A). If stomate i is centered at (xi, yi), the two slopes of tangency as function of pathogen position are:
where
Note that i ∈ {1, 2, 3}, indexing the three stomata in the focal triangle. The angle in radians between ti,1(xp, yp) and ti,2(xp, yp) is:
I further assumed that the longer distance a pathogen must travel, the less likely it would be to locate a stomate. For example, if stomata are at very low density, then a pathogen may die before it reaches a stomate because of UV, desiccation, or another factor. I included this effect by assuming the probability of reaching a stomate declines exponentially at rate H with the Euclidean distance vi(xp, yp) between the pathogen location and the edge of stomata i, which is distance R from its center at xi, yi:
The probability of locating a stomate as a function of pathogen position (xp and yp) is the sum of the angles divided by 2π, discounted by their distance from the stomate:
When there is no pathogen death (H = 0), plocate is the fraction of angles that lead from (xp, yp) to a stomate. When H > 0, plocate is proportional to this fraction, but less than it depending on stomatal density, size, and starting location of the pathogen.
To obtain the average plocate, we must integrate flocate(xp, yp) over all possible starting positions (xp, yp) within the focal area. The focal area is a 30–60–90 triangle with vertices at the center of the reference stomate (0, 0), the midpoint of baseline (U/2, 0), and the centroid of the focal triangle (Figure 1C). Colonization occurs with probability 1 if the pathogen lands in the reference stomate, so we need to integrate the probability of colonization if it lands elsewhere. This region extends from the edge of the stomate, at to U/2 (Figure 2B). At any x, we integrate from the bottom of the focal area (ymin) to the top (ymax):
The integral is:
afocal is the area of the focal region depicted in gray in Figure 2B:
Materials and Methods
The Model calculates a probability of host colonization (Equation 5) as a function of stomatal density, size, and position of a pathogen on the leaf. I solved pcolonize by importing symbolic derivations from Sympy into R with reticulate version 1.16 (Ushey et al., 2020) and used the integral2() function in the pracma package version 2.2.9 (Borchers, 2019) for numerical integration. I used R version 4.0.2 (R Core Team, 2020) for all analyses and wrote the paper in rmarkdown version 2.3 (Xie et al., 2018; Allaire et al., 2020). Citations for additional R software packages are in Appendix 2. Source code is deposited on GitHub (https://github.com/cdmuir/stomata-tradeoff) and archived on Zenodo (https://doi.org/10.5281/zenodo.4102283).
What Is the Relationship Between Stomatal Size, Density, and Colonization?
I calculated pcolonize over a biologically plausible grid of stomatal size and density for hypostomatous species based on Boer et al. (2016). Stomatal density (D) ranges from 101 to 103.5 mm−2; stomatal size (S) ranges from 101 to 103.5 μm2. I only considered combinations of size and density where stomatal cover (fS) was <1/3, which is close to the upper limit in terrestrial plants (Boer et al., 2016). I crossed stomatal traits with three levels of H ∈ {0, 0.01, 0.1}. When H = 0, a pathogen persists indefinitely on the leaf surface. H = 0.01 and H = 0.1 correspond to low and high death rates, respectively. These values are not necessarily realistic, but illustrate qualitatively how a hostile environment on the leaf surface alters model predictions.
How Do Pathogens Alter Optimal Stomatal Size-Density Scaling?
The stomatal size-density scaling relationship can be explained in terms of preserving a constant stomatal conductance (gs,max) that is proportional to DS0.5 when bm is constant (Equation 1). In other words, there are infinitely many combinations of D and S0.5 with the same gs,max. If gs,max is held constant at Cg, then the resulting size-density scaling relationship on a log-log scale is:
where lowercase variables are log-transformed equivalents of their uppercase counterparts (Table 1). The scaling exponent βg = 0.5 preserves Cg.
Next, suppose there is a scaling exponent βp that preserves pcolonize for the product . If βp = 0.5, then pcolonize is always proportional to gs,max. If βp > 0.5, small, densely packed stomata would be more resistant to colonization (lower pcolonize) compared to larger, sparsely spaced stomata with the same gs,max. If βp < 0.5, small, densely packed stomata would be less defended (higher pcolonize) compared to larger, sparsely spaced stomata with the same gs,max. I refer to the three outcomes (βp = 0.5, βp < 0.5, and βp > 0.5) as iso-, hypo-, and hyper-conductance, respectively. I was unable to solve analytically for βp, so I numerically calculated isoclines of pcolonize over the grid of D and S values described in the preceding subsection. I numerically calculated the scaling relationships at a constant pcolonize ∈ {0.025, 0.1, 0.4} for H ∈ {0, 0.01, 0.1}.
Results
Non-linear Relationships Between Colonization, Stomatal Cover, and Conductance
The probability of colonization (pcolonize) is not simply proportional to stomatal cover (fS). At low fS, pcolonize increases rapidly relative to fS at first (Figure 3A). At higher fS, pcolonize increases linearly with fS. When pathogens persist indefinitely (H = 0), any combination of stomatal size (S) and density (D) with the same fS have the same effect on pcolonize. When H > 0, pathogens are less likely to land close enough to a stomate to infect before dying, so pcolonize is closer to fS (Figure 3A). The maximum pcolonize under the range of parameters considered was ~ 0.6 when H = 0 and fS is at its maximum value of 1/3. When fS is low, pcolonize is also low. The relationship between pcolonize, fS, and gs, maxis qualitatively similar in the spatially implicit model, but the values for pcolonize are substantially higher because pathogens can potentially colonize any stomate on the leaf rather than only those in the focal triangle (see Appendix 1: Spatially Implicit Model for more detail). Bear in mind that this is the probability for a single individual searching randomly; if enough individuals reach the leaf and/or they can actively find stomata, it's almost certain that at least some will colonize the leaf. However, reducing pcolonize may help plants limit the damage since fewer total individual pathogens will colonize the leaf interior.
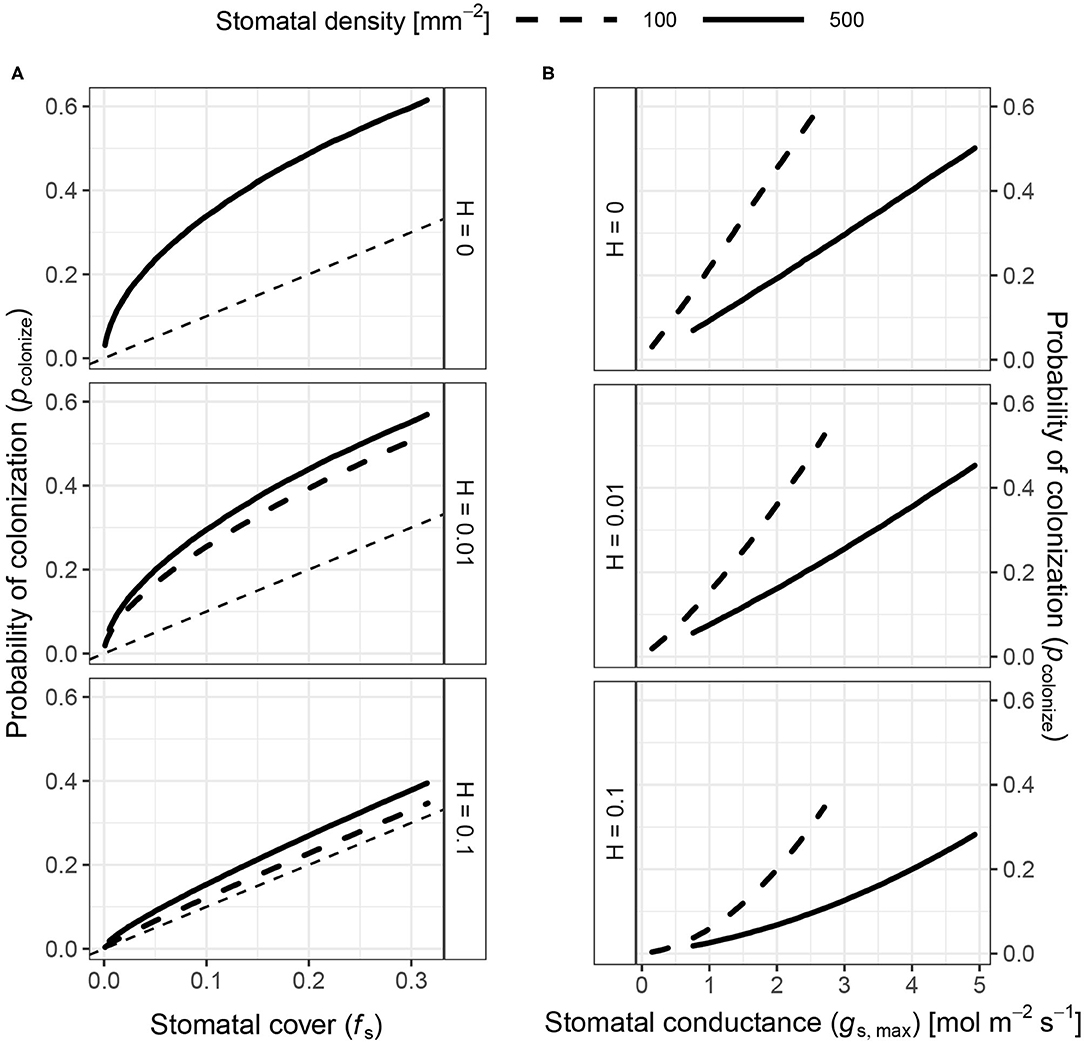
Figure 3. The probability of colonization increases with both stomatal cover and conductance. I simulated the probability of colonization (pcolonize, y-axis) over a range of stomatal densities and sizes (see Materials and Methods), but a subset of results are shown here. Stomatal size and density determine stomatal cover (fS; Equation 1) and theoretical maximum stomatal conductance (gs,max; Equation 1). (A) pcolonize initially increases rapidly with fS (x-axis), then slows down to a linear relationship. Overall, pcolonize is lower when pathogens can die on the leaf surface (H > 0). The relationship between fS and pcolonize is the same regardless of stomatal density when H = 0 (upper facet), which is why the lines overlap. When H > 0, higher density (solid lines) increase pcolonize (lower facets). (B) pcolonize increases exponentially with gs,max at all stomatal densities, but pcolonize is much lower at higher densities for a given gs,max. The relationship between gs,max and pcolonize is similar for all values of H.
pcolonize is not directly proportional to fS because it depends on D and S in quantitatively different ways (Supplementary Figure 1). For the same fS, leaves with greater D have higher pcolonize (Figure 3A). Holding fS constant, leaves with lower D and higher S will have a greater distance (vi) between a pathogen and its stomata. When H > 0, this extra distance leads more pathogens to die before they can find a stomate. However, this result is inconsistent with the spatially implicit model (Appendix 1) because S and D have identical effects on fS.
In contrast to fS, pcolonize increases at a greater than linear rate with stomatal conductance (gs,max). Greater D (smaller S) is associated with lower pcolonize for a given value of gs,max (Figure 3B). This happens because pcolonize increases approximately linearly with S whereas gs,max is proportional to S0.5. Therefore, pcolonize increases exponentially with gs,max at all stomatal densities, but the rate of growth is lower at greater D for a given value of gs,max.
Hyper-Conductance Size-Density Scaling
The scaling relationship between S and D that preserves pcolonize is always >0.5 (hyper-conductance), but usually <1. When H = 0, the scaling relationship is essentially 1 (Figure 4), which means that an increase fS leads to a proportional increase in pcolonize. Because the scaling relationship is >0.5, leaves with greater stomatal density will have lower pcolonize than leaves lower stomatal density but the same gs,max. In other words, increasing D and lowering S allows plants to reduce pcolonize while maintaining gs,max. The scaling relationship is slightly <1, but still >0.5, when H > 0 (Figure 4). In this area of parameter space, lower stomatal density can reduce fS while pcolonize is constant, but this will still result in lower gs,max. In the spatially implicit model, the size-density scaling exponent was always exactly 1 except when H = 0 (Appendix 1).
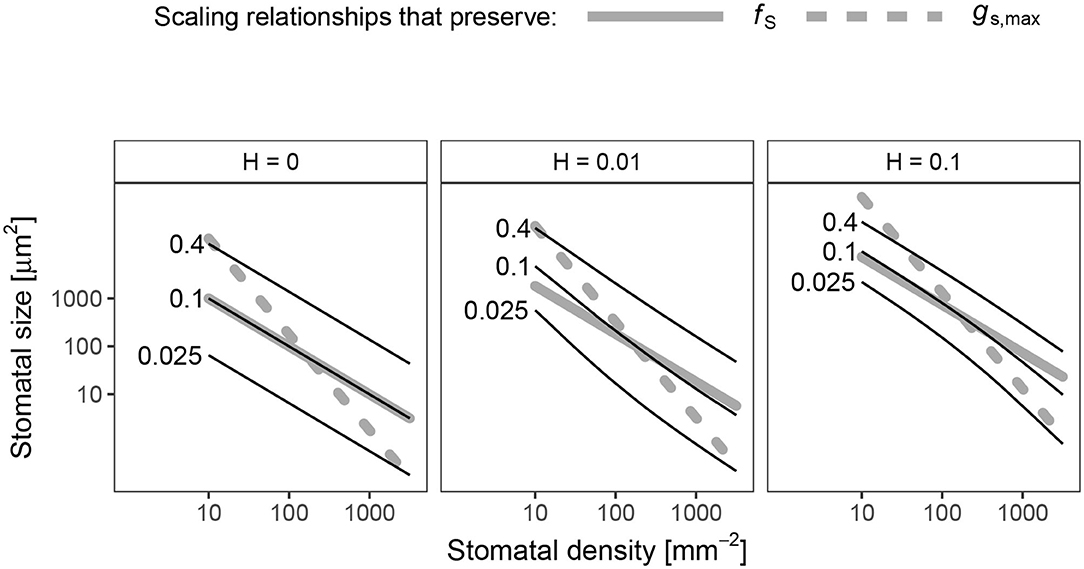
Figure 4. Log-log scaling relationships between stomatal density (D, x-axis) and size (S, y-axis) that preserve the probability of colonization (pcolonize). In each panel, solid lines indicate values of D and S where pcolonize is 0.025 (lowest line), 0.1, or 0.4 (highest line). For reference, dashed gray lines show scaling relationships that preserve fS (β = 1, slope = −1/β = −1) and gs,max (β = 0.5, slope = −1/β = −2) drawn through the centroid of the plotting region. When the death rate on the leaf surface is low (H = 0), the scaling exponent is very close to β = 1. When H > 0, 0.5 < β < 1 and is slightly non-linear on a log-log scale.
Discussion
Stomatal density and size set the upper limit on gas exchange in leaves (Harrison et al., 2019) and is often closely related to operational stomatal conductance in nature (Murray et al., 2019). Despite the fact that many foliar pathogens infect through stomata, the relationship between stomatal anatomy and resistance to foliar pathogens is less clear than it is for gas exchange. I used a spatially explicit model of a pathogen searching for a stomate to colonize a host. From this Model, I derived predictions about the relationship between stomatal anatomy and the probability of colonization, a component of disease resistance. The model predicts that the probability of colonization is not always proportional to the surface area of leaf covered by stomata (fS), as one might intuitively predict. If the leaf surface is a hostile environment and pathogens have a limited time to search, lower stomatal density decreases the probability of colonization even if fS is constant. However, gs,max decreases proportionally more than the probability of colonization. The model highlights the potential for conflicting demands of minimizing pathogen colonization, minimizing stomatal cover, and maintaining stomatal conductance. Including the effect of anatomy on pathogen colonization therefore has the potential to change our understanding of how stomatal size-density scaling evolves in land plants.
The model predicts that in most cases, increasing stomatal cover should lead to a proportional increase in colonization, which agrees with empirical studies (e.g., McKown et al., 2014; Dutton et al., 2019; Fetter et al., 2019; Tateda et al., 2019). It also makes new, testable predictions that are less intuitive (Table 2). At very low fS, there is a rapid increase in colonization (Figure 3A). If there are no stomata, the probability of colonization is 0, so the first few stomata dramatically increase the probability. This is less likely to be significant for abaxial (lower) leaf surfaces, which usually have most of the stomata (Salisbury, 1928; Metcalfe and Chalk, 1950; Mott et al., 1984; Peat and Fitter, 1994; Jordan et al., 2014; Muir, 2015; Bucher et al., 2017; Drake et al., 2019). However, many adaxial (upper) leaf surfaces have zero or very few stomata. Using adaxial leaf surfaces, it should be possible to test if small changes in stomatal size or density have a larger effect on pathogen colonization when fS is low. Such experiments could use natural genetic variation (McKown et al., 2014) or mutant lines (Dow et al., 2014b). The non-linear increase in pcolonize is less apparent when H > 0 (Figure 3A). A more hostile microenvironment (e.g., drier, higher UV) should therefore reduce the effect of increased size or density at low fS. If true, the diminishing marginal effect of fS on colonization could explain why stomatal ratio on the upper and lower surface is bimodal (Muir, 2015). The initial cost of adaxial (upper) stomata is relatively high, but if the benefits outweigh the costs, then equal stomatal densities on each surface maximize CO2 supply for photosynthesis (Parkhurst, 1978; Gutschick, 1984; Parkhurst and Mott, 1990). The costs and benefits will certainly vary with environmental conditions as well. Future work should extend this model, which considered hypostomatous leaves, to address stomatal size and density in amphistomatous leaves, since leaf surfaces may differ in the type of pathogens present and microenvironment (McKown et al., 2014; Fetter et al., 2019).
An effect of stomatal size and density on foliar pathogen colonization could change our understanding of stomatal size-density scaling. Since allocating leaf epidermis to stomata may be costly (Assmann and Zeiger, 1987; Franks and Farquhar, 2007; Dow et al., 2014b; Lehmann and Or, 2015; Baresch et al., 2019), selection should favor leaves that achieve a desired gs,max while minimizing fS (Boer et al., 2016). Because of their different scaling exponents (Equation 1, 2), smaller, densely packed stomata can achieve the same gs,max at minimum fS. However, many leaves have larger, sparsely packed stomata. Incorporating pathogen colonization may explain why. If pathogens have a limited time to find stomata before dying (H > 0), then the scaling exponent between size and density that keeps pcolonize constant is between 0.5 and 1, the scaling exponents for gs,max and fS, respectively (Figure 4). Greater density of smaller stomata can increase gs,max while keeping pcolonize constant, but this will increase fS. Conversely, fS could decrease while keeping pcolonize constant, but this will decrease gs,max. This sets up the potential for conflict between competing goals. The optimal stomatal size and density will therefore depend on the precise costs and benefits of infection, stomatal conductance, and stomatal cover. This may explain why many leaves have large, sparsely packed stomata despite the fact that they could achieve the same gs,max and lower fS with smaller, more densely packed stomata.
The model examines the probability of colonization for a single pathogen. The calculated probabilities of colonization should not be interpreted as exact predictions, but rather as depicting qualitative relationships between stomatal anatomy and infection severity. The energetic cost and lost photosynthetic capacity (closed stomata, necrosis, etc.) of dealing with a pathogen is assumed to be proportional to the amount of infection. The actual fitness cost will be modulated by the number of pathogens landing on the leaf and the cost of infection, all else being equal. In environments with fewer or less virulent pathogens, the fitness cost of infection will be less than in environments with more abundant, virulent pathogens. The model is less relevant to very susceptible host plants that can be severely damaged or killed by a small number of colonizations that spread unchecked throughout the host tissue.
Conclusion
The model makes two non-intuitive predictions. First, the effect of increased stomatal density or size on susceptibility to foliar pathogens is greatest when stomatal cover is very low. Second, maximizing disease resistance sets up a potential conflict between minimizing stomatal cover and maximizing stomatal conductance. The first prediction is consistent with results in Populus trichocarpa (McKown et al., 2014) and may be relatively straightforward to test experimentally with adaxial (upper) stomata that occur at low and moderate densities within the same or closely related species (Muir et al., 2014; Fetter et al., 2019). The second prediction about size-density scaling is more complex because we would need to know the relationships between colonization, stomatal cover, stomatal conductance, and fitness in natural conditions. There is growing evidence that stomata mediate tradeoffs between photosynthesis and defense in Populus trichocarpa (McKown et al., 2019), but testing these predictions in a variety of species will help determine whether pathogens have played an important role shaping stomatal anatomy in land plants.
Data Availability Statement
Source code is deposited on GitHub (https://github.com/cdmuir/stomata-tradeoff) and archived on Zenodo (https://doi.org/10.5281/zenodo.4102283).
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
I am grateful startup funds from the University of Hawai'i for supporting this work.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I would like to thank Athena McKown and Karl Fetter for valuable feedback that improved this manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2020.518991/full#supplementary-material
Appendix 1. Supplemental methods and spatially implicit model.
Appendix 2. Additional R packages.
References
Allaire, J., Xie, Y., McPherson, J., Luraschi, J., Ushey, K., Wickham, H., et al. (2020). Rmarkdown: Dynamic Documents for R. Available online at: https://github.com/rstudio/rmarkdown.
Allen, E. A., Hazen, B. E., Hoch, H. C., Kwon, Y., Leinhos, G. M. E., Staples, R. C., et al. (1991). Appressorium formation in response to topographical signals by 27 rust species. Phytopathology 81:323. doi: 10.1094/Phyto-81-323
Assmann, S. M., and Zeiger, E. (1987). “Guard call bioenergetics,” in Stomatal Function, eds E. Zeiger, G. D. Farquhar, and I. R. Cowan (Stanford, CA: Stanford University Press), 163–193.
Baresch, A., Crifò, C., and Boyce, C. K. (2019). Competition for epidermal space in the evolution of leaves with high physiological rates. New Phytol. 221, 628–639. doi: 10.1111/nph.15476
Bastiaans, L. (1991). Ratio between virtual and visual lesion size as a measure to describe reduction in leaf photosynthesis of rice due to leaf blast. Phytopathology 81:611. doi: 10.1094/Phyto-81-611
Beattie, G. A., and Lindow, S. E. (1995). The secret life of foliar bacterial pathogens on leaves. Annu. Rev. Phytopathol. 33, 145–172.
Berry, J. A., Beerling, D. J., and Franks, P. J. (2010). Stomata: key players in the earth system, past and present. Curr. Opin. Plant Biol. 13, 232–239. doi: 10.1016/j.pbi.2010.04.013
Boer, H. J., de Price, C. A., Wagner-Cremer, F., Dekker, S. C., Franks, P. J., and Veneklaas, E. J. (2016). Optimal allocation of leaf epidermal area for gas exchange. New Phytol. 210, 1219–1228. doi: 10.1111/nph.13929
Borchers, H. W. (2019). Pracma: Practical Numerical Math Functions. R package version 2.2.9. Available online at: https://CRAN.R-project.org/package=pracma.
Brand, A., and Gow, N. A. R. (2012). “Tropic orientation responses of pathogenic fungi,” in Morphogenesis and Pathogenicity in Fungi, eds J. Pérez-Martín and A. Di Pietro (Berlin; Heidelberg: Springer Berlin Heidelberg), 21–41. doi: 10.1007/978-3-642-22916-9_2
Brodribb, T. J., Jordan, G. J., and Carpenter, R. J. (2013). Unified changes in cell size permit coordinated leaf evolution. New Phytol. 199, 559–570. doi: 10.1111/nph.12300
Brown, H. T., and Escombe, F. (1900). Static diffusion of gases and liquids in relation to the assimilation of carbon and translocation in plants. Proc. R. Soc. Lond. 67, 124–128.
Bucher, S. F., Auerswald, K., Grün-Wenzel, C., Higgins, S. I., Garcia Jorge, J., and Römermann, C. (2017). Stomatal traits relate to habitat preferences of herbaceous species in a temperate climate. Flora 229, 107–115. doi: 10.1016/j.flora.2017.02.011
Buckley, T. N. (2019). How do stomata respond to water status? New Phytol. 224, 21–36. doi: 10.1111/nph.15899
Chater, C. C. C., Caine, R. S., Fleming, A. J., and Gray, J. E. (2017). Origins and evolution of stomatal development. Plant Physiol. 174, 624–638. doi: 10.1104/pp.17.00183
Dow, G. J., Bergmann, D. C., and Berry, J. A. (2014a). An integrated model of stomatal development and leaf physiology. New Phytol. 201, 1218–1226. doi: 10.1111/nph.12608
Dow, G. J., Berry, J. A., and Bergmann, D. C. (2014b). The physiological importance of developmental mechanisms that enforce proper stomatal spacing in Arabidopsis thaliana. New Phytol. 201, 1205–1217. doi: 10.1111/nph.12586
Drake, P. L., Boer, H. J., Schymanski, S. J., and Veneklaas, E. J. (2019). Two sides to every leaf: Water and CO2 transport in hypostomatous and amphistomatous leaves. New Phytol. 222, 1179–1187. doi: 10.1111/nph.15652
Drake, P. L., Froend, R. H., and Franks, P. J. (2013). Smaller, faster stomata: scaling of stomatal size, rate of response, and stomatal conductance. J. Exp. Bot. 64, 495–505. doi: 10.1093/jxb/ers347
Dutton, C., Hõrak, H., Hepworth, C., Mitchell, A., Ton, J., Hunt, L., et al. (2019). Bacterial infection systemically suppresses stomatal density. Plant Cell Environ. 42, 2411–2421. doi: 10.1111/pce.13570
Farquhar, G. D., and Sharkey, T. D. (1982). Stomatal conductance and photosynthesis. Annu. Rev. Plant Physiol. 33, 317–345. doi: 10.1146/annurev.pp.33.060182.001533
Fawke, S., Doumane, M., and Schornack, S. (2015). Oomycete interactions with plants: infection strategies and resistance principles. Microbiol. Mol. Biol. Rev. 79, 263–280. doi: 10.1128/MMBR.00010-15
Fetter, K. C., Nelson, D. M., and Keller, S. R. (2019). Trade-Offs and Selection Conflicts in Hybrid Poplars Indicate the Stomatal Ratio as an Important Trait Regulating Disease Resistance. Burlington, VT: University of Vermont.
Flexas, J., Cano, F. J., Carriquí, M., Coopman, R. E., Mizokami, Y., Tholen, D., et al. (2018). “CO2 diffusion inside photosynthetic organs,” in The Leaf: A Platform for Performing Photosynthesis Advances in Photosynthesis and Respiration, eds W. W. Adams III and I. Terashima (Cham: Springer International Publishing), 163–208. doi: 10.1007/978-3-319-93594-2_7
Franks, P. J., and Beerling, D. J. (2009a). CO 2 -forced evolution of plant gas exchange capacity and water-use efficiency over the Phanerozoic. Geobiology 7, 227–236. doi: 10.1111/j.1472-4669.2009.00193.x
Franks, P. J., and Beerling, D. J. (2009b). Maximum leaf conductance driven by CO2 effects on stomatal size and density over geologic time. Proc. Natl. Acad. Sci. U.S.A. 106, 10343–10347. doi: 10.1073/pnas.0904209106
Franks, P. J., Drake, P. L., and Beerling, D. J. (2009). Plasticity in maximum stomatal conductance constrained by negative correlation between stomatal size and density: an analysis using Eucalyptus globulus. Plant Cell Environ. 32, 1737–1748. doi: 10.1111/j.1365-3040.2009.002031.x
Franks, P. J., and Farquhar, G. D. (2001). The effect of exogenous abscisic acid on stomatal development, stomatal mechanics, and leaf gas exchange in Tradescantia virginiana. Plant Physiol. 125, 935–942. doi: 10.1104/pp.125.2.935
Franks, P. J., and Farquhar, G. D. (2007). The mechanical diversity of stomata and its significance in gas-exchange control. Plant Physiol. 143, 78–87. doi: 10.1104/pp.106.089367
Franks, P. J., Royer, D. L., Beerling, D. J., Van de Water, P. K., Cantrill, D. J., Barbour, M. M., et al. (2014). New constraints on atmospheric CO2 concentration for the Phanerozoic. Geophys. Res. Lett. 41, 4685–4694. doi: 10.1002/2014GL060457
Gilbert, G. S. (2002). Evolutionary ecology of plant diseases in naturalecosystems. Annu. Rev. Phytopathol. 40, 13–43. doi: 10.1146/annurev.phyto.40.021202.110417
Gray, A., Liu, L., and Facette, M. (2020). Flanking support: how subsidiary cells contribute to stomatal form and function. Front. Plant Sci. 11:881. doi: 10.3389/fpls.2020.00881
Gutschick, V. P. (1984). Photosynthesis model for C3 leaves incorporating CO2 transport, propagation of radiation, and biochemistry 1. Kinetics and their parameterization. Photosynthetica 18, 549–568.
Harrison, E. L., Arce Cubas, L., Gray, J. E., and Hepworth, C. (2019). The influence of stomatal morphology and distribution on photosynthetic gas exchange. Plant J. 101, 768–779. doi: 10.1111/tpj.14560
Hetherington, A. M., and Woodward, F. I. (2003). The role of stomata in sensing and driving environmental change. Nature 424, 901–908. doi: 10.1038/nature01843
Hoch, H. C., Staples, R. C., Whitehead, B., Comeau, J., and Wolf, E. D. (1987). Signaling for growth orientation and cell differentiation by surface topography in uromyces. Science 235, 1659–1662.
Jones, H. G. (1985). Partitioning stomatal and non-stomatal limitations to photosynthesis. Plant Cell Environ. 8, 95–104. doi: 10.1111/j.1365-3040.1985.tb01227.x
Jordan, G. J., Carpenter, R. J., and Brodribb, T. J. (2014). Using fossil leaves as evidence for open vegetation. Palaeogeogr. Palaeoclimatol. Palaeoecol. 395, 168–175. doi: 10.1016/j.palaeo.2013.12.035
Kiefer, B., Riemann, M., Büche, C., Kassemeyer, H.-H., and Nick, P. (2002). The host guides morphogenesis and stomatal targeting in the grapevine pathogen Plasmopara viticola. Planta 215, 387–393. doi: 10.1007/s00425-002-0760-2
Lawson, T., and Blatt, M. R. (2014). Stomatal size, speed, and responsiveness impact on photosynthesis and water use efficiency. Plant Physiol. 164, 1556–1570. doi: 10.1104/pp.114.237107
Lawson, T., Terashima, I., Fujita, T., and Wang, Y. (2018). “Coordination between photosynthesis and stomatal behavior,” in The Leaf: A Platform for Performing Photosynthesis Advances in Photosynthesis and Respiration, eds W. W. Adams III and I. Terashima (Cham: Springer International Publishing), 141–161. doi: 10.1007/978-3-319-93594-2_6
Lehmann P. Or D. (2015). Effects of stomata clustering on leaf gas exchange. New Phytol. 207, 1015–1025. doi: 10.1111/nph.13442
McElwain, J. C., Yiotis, C., and Lawson, T. (2016). Using modern plant trait relationships between observed and theoretical maximum stomatal conductance and vein density to examine patterns of plant macroevolution. New Phytol. 209, 94–103. doi: 10.1111/nph.13579
McKown, A. D., Guy, R. D., Quamme, L., Klápště, J., La Mantia, J., Constabel, C. P., et al. (2014). Association genetics, geography and ecophysiology link stomatal patterning in Populus trichocarpa with carbon gain and disease resistance trade-offs. Mol. Ecol. 23, 5771–5790. doi: 10.1111/mec.12969
McKown, A. D., Klápště, J., Guy, R. D., Corea, O. R. A., Fritsche, S., Ehlting, J., et al. (2019). A role for SPEECHLESS in the integration of leaf stomatal patterning with the growth vs disease trade-off in poplar. New Phytol. 223, 1888–1903. doi: 10.1111/nph.15911
McLachlan, D. H., Kopischke, M., and Robatzek, S. (2014). Gate control: guard cell regulation by microbial stress. New Phytol. 203, 1049–1063. doi: 10.1111/nph.12916
Melotto, M., Underwood, W., Koczan, J., Nomura, K., and He, S. Y. (2006). Plant stomata function in innate immunity against bacterial invasion. Cell 126, 969–980. doi: 10.1016/j.cell.2006.06.054
Melotto, M., Zhang, L., Oblessuc, P. R., and He, S. Y. (2017). Stomatal defense a decade later. Plant Physiol. 174, 561–571. doi: 10.1104/pp.16.01853
Metcalfe, C. R., and Chalk, L. (1950). Anatomy of the Dicotyledons, Vols. 1 & 2. Oxford: Oxford University Press.
Meurer, A., Smith, C. P., Paprocki, M., Čertík, O., Kirpichev, S. B., Rocklin, M., et al. (2017). SymPy: symbolic computing in Python. PeerJ Comput. Sci. 3:e103. doi: 10.7717/peerj-cs.103
Mitchell, C. E. (2003). Trophic control of grassland production and biomass by pathogens. Ecol. Lett. 6, 147–155. doi: 10.1046/j.1461-0248.2003.00408.x
Morison, J. I. L., Emily Gallouët Lawson, T., Cornic, G., Herbin, R., and Baker, N. R. (2005). Lateral diffusion of CO$_2$ in leaves is not sufficient to support photosynthesis. Plant Physiol. 139, 254–266. doi: 10.1104/pp.105.062950
Mott, K. A., Gibson, A. C., and O'Leary, J. W. (1984). The adaptive significance of amphistomatic leaves. Plant Cell Environ. 5, 455–460.
Muir, C. D. (2015). Making pore choices: repeated regime shifts in stomatal ratio. Proc. R. Soc. B Biol. Sci. 282:20151498. doi: 10.1098/rspb.2015.1498
Muir, C. D., Hangarter, R. P., Moyle, L. C., and Davis, P. A. (2014). Morphological and anatomical determinants of mesophyll conductance in wild relatives of tomato (solanum sect. Lycopersicon, sect. Lycopersicoides; Solanaceae). Plant Cell Environ. 37, 1415–1426. doi: 10.1111/pce.12245
Murray, M., Soh, W. K., Yiotis, C., Spicer, R. A., Lawson, T., and McElwain, J. C. (2019). Consistent relationship between field-measured stomatal conductance and theoretical maximum stomatal conductance in C3 woody angiosperms in four major biomes. Int. J. Plant Sci. 181:706260. doi: 10.1086/706260
Murray, R. R., Emblow, M. S. M., Hetherington, A. M., and Foster, G. D. (2016). Plant virus infections control stomatal development. Sci. Rep. 6:34507. doi: 10.1038/srep34507
Oguchi, R., Onoda, Y., Terashima, I., and Tholen, D. (2018). “Leaf anatomy and function,” in The Leaf: A Platform for Performing Photosynthesis Advances in Photosynthesis and Respiration, eds W. W. Adams III and I. Terashima (Cham: Springer International Publishing), 97–139. doi: 10.1007/978-3-319-93594-2_5
Papanatsiou, M., Amtmann, A., and Blatt, M. R. (2017). Stomatal clustering in Begonia associates with the kinetics of leaf gaseous exchange and influences water use efficiency. J. Exp. Bot. 68, 2309–2315. doi: 10.1093/jxb/erx072
Parkhurst, D. F. (1978). The adaptive significance of stomatal occurrence on one or both surfaces of leaves. J. Ecol. 66:367. doi: 10.2307/2259142
Parkhurst, D. F., and Mott, K. A. (1990). Intercellular diffusion limits to CO 2 uptake in leaves: studies in Air and Helox. Plant Physiol. 94, 1024–1032. doi: 10.1104/pp.94.3.1024
Parlange, J.-Y., and Waggoner, P. E. (1970). Stomatal dimensions and resistance to diffusion. Plant Physiol. 46, 337–342. doi: 10.1104/pp.46.2.337
Peat, H. J., and Fitter, A. H. (1994). A comparative study of the distribution and density of stomata in the British flora. Biol. J. Linn. Soc. 52, 377–393.
R Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: http://www.R-project.org/.
Raissig, M. T., Matos, J. L., Anleu Gil, M. X., Kornfeld, A., Bettadapur, A., Abrash, E., et al. (2017). Mobile MUTE specifies subsidiary cells to build physiologically improved grass stomata. Science 355, 1215–1218. doi: 10.1126/science.aal3254
Sack, L., and Buckley, T. N. (2016). The developmental basis of stomatal density and flux. Plant Physiol. 171, 2358–2363. doi: 10.1104/pp.16.00476
Sack, L., Cowan, P. D., Jaikumar, N., and Holbrook, N. M. (2003). The ‘hydrology’ of leaves: co-ordination of structure and function in temperate woody species. Plant Cell Environ. 26, 1343–1356. doi: 10.1046/j.0016-8025.2003.01058.x
Salisbury, E. J. (1928). On the causes and ecological significance of stomatal frequency, with special reference to the Woodland Flora. Philos. Trans. R. Soc. B Biol. Sci. 216, 1–65. doi: 10.1098/rstb.1928.0001
Tateda, C., Obara, K., Abe, Y., Sekine, R., Nekoduka, S., Hikage, T., et al. (2019). The host stomatal density determines resistance to Septoria gentianae in Japanese Gentian. Mol. Plant Microbe Interact. 32, 428–436. doi: 10.1094/MPMI-05-18-0114-R
Tichá, I. (1982). Photosynthetic characteristics during ontogenesis of leaves 7. Stomata density and sizes. Photosynthetica 16, 375–471.
Tucker, S. L., and Talbot, N. J. (2001). Surface attachment and pre-penetration stage development by plant pathogenic fungi. Annu. Rev. Phytopathol. 39, 385–417. doi: 10.1146/annurev.phyto.39.1.385
Underwood, W., Melotto, M., and He, S. Y. (2007). Role of plant stomata in bacterial invasion. Cell. Microbiol. 9, 1621–1629. doi: 10.1111/j.1462-5822.2007.00938.x
Ushey, K., Allaire, J. J., and Tang, Y. (2020). Reticulate: Interface to ‘Python’. Available online at: https://CRAN.R-project.org/package=reticulate.
Weiss, A. (1865). Untersuchungen über die Zahlen- und Grössenverhältnisse der Spaltöffnungen. Jahr. Wissensch. Bot. 4, 125–196.
Xie, Y., Allaire, J. J., and Grolemund, G. (2018). R Markdown: The Definitive Guide. Boca Raton, FL: Taylor & Francis, CRC Press.
Keywords: anatomy, leaf gas exchange, model, pathogen, photosynthesis, scaling, stomata, tradeoff
Citation: Muir CD (2020) A Stomatal Model of Anatomical Tradeoffs Between Gas Exchange and Pathogen Colonization. Front. Plant Sci. 11:518991. doi: 10.3389/fpls.2020.518991
Received: 10 December 2019; Accepted: 01 October 2020;
Published: 29 October 2020.
Edited by:
Graham Dow, ETH Zürich, SwitzerlandReviewed by:
Athena McKown, University of British Columbia, CanadaKarl C. Fetter, University of Georgia, United States
Copyright © 2020 Muir. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christopher D. Muir, Y2RtdWlyQGhhd2FpaS5lZHU=
 Christopher D. Muir
Christopher D. Muir