- 1Karlsruhe Institute of Technology, Institute of Meteorology and Climate Research - Atmospheric Environmental Research (IMK-IFU), Garmisch-Partenkirchen, Germany
- 2University of Bayreuth, Chair of Plant Ecology, Bayreuth, Germany
- 3Department of Botany, University of Innsbruck, Innsbruck, Austria
During drought, trees reduce water loss and hydraulic failure by closing their stomata, which also limits photosynthesis. Under severe drought stress, other acclimation mechanisms are trigged to further reduce transpiration to prevent irreversible conductance loss. Here, we investigate two of them: the reversible impacts on the photosynthetic apparatus, lumped as non-stomatal limitations (NSL) of photosynthesis, and the irreversible effect of premature leaf shedding. We integrate NSL and leaf shedding with a state-of-the-art tree hydraulic simulation model (SOX+) and parameterize them with example field measurements to demonstrate the stress-mitigating impact of these processes. We measured xylem vulnerability, transpiration, and leaf litter fall dynamics in Pinus sylvestris (L.) saplings grown for 54 days under severe dry-down. The observations showed that, once transpiration stopped, the rate of leaf shedding strongly increased until about 30% of leaf area was lost on average. We trained the SOX+ model with the observations and simulated changes in root-to-canopy conductance with and without including NSL and leaf shedding. Accounting for NSL improved model representation of transpiration, while model projections about root-to-canopy conductance loss were reduced by an overall 6%. Together, NSL and observed leaf shedding reduced projected losses in conductance by about 13%. In summary, the results highlight the importance of other than purely stomatal conductance-driven adjustments of drought resistance in Scots pine. Accounting for acclimation responses to drought, such as morphological (leaf shedding) and physiological (NSL) adjustments, has the potential to improve tree hydraulic simulation models, particularly when applied in predicting drought-induced tree mortality.
Introduction
There is increasing evidence that hydraulic failure is a main trigger of tree death in response to drought and hot drought (Allen et al., 2015; McDowell et al., 2018; Brodribb et al., 2020). While trees are well-adapted to respond to seasonal and short-term increases in soil and atmospheric drought, extreme climatic conditions, e.g., anomalously high summer temperatures coupled with low soil water availability, as experienced, for instance, in central Europe during the summer of 2018 (Hari et al., 2020; Schuldt et al., 2020), can cause substantial hot drought-induced damage. Increasing soil and atmospheric drought result in increasing tree internal water column tensions. As such tensions rise, air bubbles, i.e., emboli, can form in the xylem, reducing xylem hydraulic conductance (Tyree and Ewers, 1991). Reduced xylem conductance limits water transport upward, from soil to the leaves, which may lead to dehydration of cambium and apical meristems, canopy dieback, and ultimately tree death (e.g., Carnicer et al., 2011; Anderegg et al., 2012; Allen et al., 2015; Choat et al., 2018; Reich et al., 2018; Hesse et al., 2019).
It is well-established that stomatal closure is the first and foremost mechanism that limits water loss and buildup of excessive xylem tension (Hall and Kaufmann, 1975; Monteith, 1995; Choat et al., 2018). This comes at a cost of reduced leaf permeability to CO2, which limits C assimilation (Martorell et al., 2014; Reich et al., 2018). Much research has focused on modeling stomatal conductance (gs) to water deficit (Damour et al., 2010; Mencuccini et al., 2019), as well as tree internal water balance after stomatal closure (e.g., Martin-St. Paul et al., 2017; Cochard et al., 2021). To date, many approaches exist that combine gs responses to decreasing soil water content (SWC) and increasing vapor pressure deficit (VPD). The approaches range from empirical relationships (e.g., Leuning, 1995), to mechanistical descriptions based on optimality theory such as maximizing C gain per unit of transpiration (e.g., Medlyn et al., 2011), maximizing transpiration while reducing conductivity loss (Sperry and Love, 2015), or maximizing C gain while minimizing loss in hydraulic conductivity (e.g., Sperry et al., 2017; Eller et al., 2018; 2020). The success of these models has been mixed, leading to a good representation of broad monthly and annual transpiration and productivity patterns but often failing to capture subtler responses arising when drought stress intensifies (e.g., Drake et al., 2017; Yang et al., 2019; De Kauwe et al., 2020; Bassiouni and Vico, 2021; Mu et al., 2021; Nadal-Sala et al., 2021). Hence, challenges to model tree drought responses and mortality persists albeit increasing developments of optimization-based tree hydraulic models over the recent years. Therefore, further model improvements regarding tree acclimation responses to drought beyond stomatal closure have been recommended (e.g., Keenan et al., 2010; Wolfe et al., 2016; Martin-St. Paul et al., 2017; Sperry et al., 2019; Gourlez de la Motte et al., 2020). To do so, controlled experiments that address specific tree physiological responses to drought provide an opportunity to improve and evaluate the performance of tree hydraulic models (e.g., Hartig et al., 2012; Medlyn et al., 2015; Dietze et al., 2018).
Under sustained drought, stomatal regulation in response to CO2 demand on the one hand and evaporation demand on the other may not be enough to mitigate hydraulic tension and prevent embolism formation in the xylem. Other responses are, thus, often triggered to reduce water loss, such as metabolic changes or increased internal resistance that then feedback to stomatal conductance, as well as accelerated senescence of various tissues. In particular, many studies report a slowdown of the photosynthetic activity during drought (e.g., Xu and Baldocchi, 2003; Keenan et al., 2010; Yang et al., 2019; Gourlez de la Motte et al., 2020). Such slowdown may have different causes such as increased mesophyll resistance (Flexas et al., 2007, 2012; Evans, 2021), drought-related enzymatic down-regulation (e.g., Flexas et al., 2004; Niinemets and Sack, 2006; Niinemets et al., 2006; Sugiura et al., 2020), and/or decreasing carbon demand (Fatichi et al., 2014). Since all these mechanisms lead to a reduction in water loss, here, we consider them in a lumped manner as non-stomatal limitations of photosynthesis (NSL), thereby enabling the consideration of this additional response process in models that are simulating stand productivity and transpiration in dependence on water availability (Zhou et al., 2013; Drake et al., 2017; Yang et al., 2019).
Another key mechanism of how trees can respond to drought is reducing their leaf area (e.g., Munné-Bosch and Alegre, 2004; Sala et al., 2010; Martin-St. Paul et al., 2013; Wolfe et al., 2016; Hochberg et al., 2017; Li et al., 2020; Schuldt et al., 2020). Drought-induced leaf senescence reduces total tree transpiration, at the expense of growth at mid-term, as rebuilding canopy structure requires extra C investment, either from non-structural carbohydrate reserves or from the assimilation of the remaining or newly grown leaves once drought stress has been released (Yan et al., 2017; Ruehr et al., 2019). Additionally, shedding leaves without full nutrient resorption imply net nutrient losses (Marchin et al., 2010; Chen et al., 2015), which may further limit photosynthesis post-drought with consequences for tree performance in the long term. Leaf shedding tends to occur after stomata closure; hence, it mainly reduces marginal loss in water via residual cuticular conductance and incomplete stomatal closure (e.g., Martin-St. Paul et al., 2017; Cardoso et al., 2020; Li et al., 2020). Under sustained drought, such water loss may be critical for tree survival (e.g., Blackman et al., 2016, 2019), especially considering that residual cuticular conductance increases with temperature (Schuster et al., 2016), leading to faster dehydration of plants particularly during heat waves. While leaf shedding, in response to drought, is routine in drought-deciduous trees (e.g., Ichie et al., 2004; Pineda-García et al., 2013; Ruehr et al., 2016), it can be rather seen as an emergency response in temperate conifers, with profound consequences for drought recovery.
Here, we aim to quantify the importance of NSL and leaf shedding mechanisms regarding hydraulic safety. To do so, we measured hydraulic vulnerability, and transpiration and leaf shedding dynamics in potted P. sylvestris L. saplings exposed to 2-month severe dry-down. Then, we trained a big-leaf canopy gas exchange simulation model based on the optimization of stomatal conductance as xylem tension increases (SOX model, Eller et al., 2018, 2020). The SOX model assumes that trees regulate stomatal conductance to maximize C uptake while minimizing loss in soil-to-root hydraulic conductance. Once the model was trained, we evaluated the importance of NSL and leaf shedding for hydraulic regulation. The initial hypotheses were the following: (1) including non-stomatal limitations of photosynthesis will improve the representation of transpiration during drought; (2) seasonal leaf shedding in pine trees is coordinated with stomata closure to reduce dehydration, and (3) according to the “leaf fuse” hypothesis (e.g., Hochberg et al., 2017) leaf shedding will mitigate mid-term losses in hydraulic conductance.
Materials and Methods
Experimental Setup
Potted P sylvestris L. saplings were grown in Garmisch-Partenkirchen, Germany (708 m above sea level, 47°28′32.9″N, 11°3′44.2″E). Three-year-old Scots pine saplings were purchased from a local tree nursery in 2018 and planted in individual pots (120 l, 55 cm in diameter, 70 cm in height; Brute, Rubbermaid, Atlanta, GA, United States) in a 6:3:1 mixture of potting substrate (No. 170, Klasmann-Deilmann, Geeste, Germany), perlite (Perligran Premium, Knauf Performance Materials GmbH, Dortmund, Germany), and quartz sand (3–6 and 0.1–0.3 mm). Slow-release fertilizer (100 g, Osmocote® Exact Standard 5-6M 15-9-12+2MgO+TE, ICL Specialty Fertilizers Benelux, The Netherlands) was added to the mixture and supplemented by liquid fertilizer (Manna® Wuxal Super; Wilhelm HaugGmbh, Ammerbuch, Germany). From May to October 2019, the saplings were kept inside the adjacent greenhouse and exposed to mild soil water limitation with air temperature ranging between 10 and 35°C, to prime the trees for the upcoming experiment. From October 2019 to July 2020, the saplings were again grown outside and irrigated once a week from May 2020 onwards. After leaf elongation was finished (mid of July), the then 5-year-old saplings (n = 16) were transferred to the greenhouse once more and irrigated to field capacity (SWC ~0.35 m3 m−3) before the drought experiment was started. To minimize soil evaporation, the top of the soil was covered with an opaque plastic sheet, which was periodically ventilated.
The greenhouse is equipped with special UV-transmissive glass, and incoming light was supplemented with plant growth lamps (T-agro 400 W; Philips, Hamburg, Germany). Air temperature and air humidity were computer-regulated (CC600, RAM Regel- und Messtechnische Apparate GmbH, Herrsching, Germany). Environmental conditions at canopy height such as photosynthetic active radiation (PQS 1, Kipp&Zonen, Delft, The Netherlands), air temperature, and relative humidity (CS215, Campbell Scientific Inc., Logan, UT, United States) were monitored and logged at 10-min intervals (CR1000; Campbell Scientific Inc., Logan, UT, United States). The environmental conditions during the experiment are shown in Figure 1.
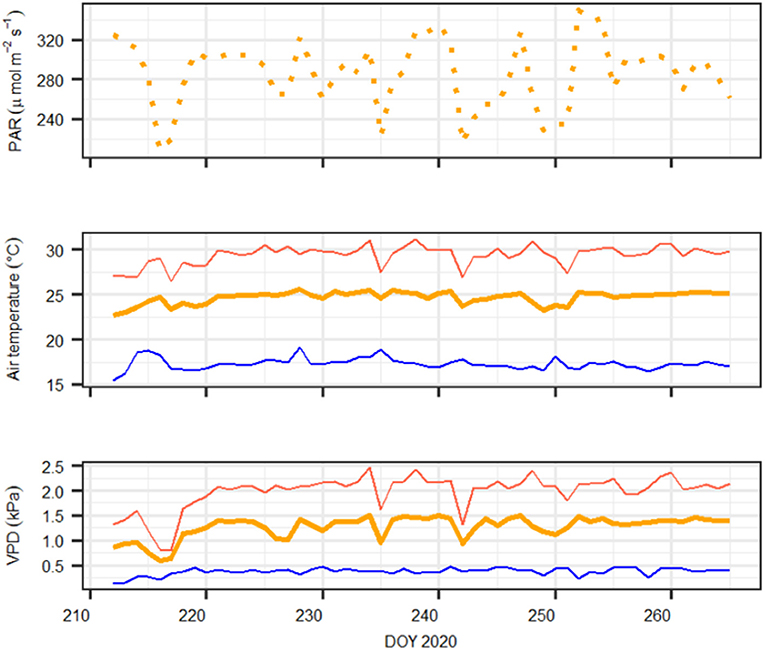
Figure 1. Daily meteorological conditions during the experiment. Upper panel: daylight average photosynthetic active radiation (PAR, in μmol m−2 s−1); middle panel: maximum (red), minimum (blue), and average (orange) air temperature (in °C); bottom panel: maximum (red), minimum (blue), and average (orange) atmospheric vapor pressure deficit (VPD, in kPa). Note that on DOY 216–217, vapor pressure deficit (VPD) and temperature conditions were lowest because of a cold weather front that was not compensated by heating the greenhouse.
Soil Water Content and Transpiration
We continuously measured soil water content (SWC) and sap flow in six randomly selected saplings. Measurements started on DOY 206, but the first week was excluded from this analysis because of plant acclimation to the new conditions, and sensor malfunction and re-calibration (data not shown). Therefore, valid measurements started on DOY 212. Volumetric SWC was monitored at 0–10 c and 40–50 cm depth (10HS; Decagon Devices Inc., Pullman, WA, United States, Supplementary Figure 1) to cover the entire rooting area. To estimate the water available for each tree, SWC data from the two depths was averaged. Each SWC sensor was pre-calibrated to the potting medium following the recommendation of the manufacturer. Stem sap flow was measured using the heat-balance method (EMS 62, EMS, Brno, Czech Republic). Sap flow sensors were installed in the upper part of the canopy (height ~1–1.5 m) as the cylindrical build does not support stem diameters >2 cm. The sensors were shielded with aluminum bubble foil to minimize error due to temperature fluctuations. Sap flow measurements were stored in 30-min intervals. Daily whole-tree transpiration was calculated by assuming that transpiration per unit of leaf area (see section Tree Biomass Compartment Measurement) was equal above and below the sensor, as in a homogeneously coupled non-shadowed canopy we expected the environmental drivers to be homogeneous for the leaves above and below. Therefore, transpiration was calculated as the sum of the measured sap flow plus the sap flow needed to supply the transpiration of the leaves below the sensor (Equation 1)
where Tr is the daily whole-tree transpiration (in kg day−1 tree−1), J is the daily sap flow (in kg day−1 tree−1), and LAbelow/LAabove is the proportion between the leaf area below the sensor in relation to the leaf area above the sensor (in m−2 tree−1).
Tree Biomass Compartment Measurement
Loss in leaf biomass was assessed once a week as follows. We collected and carefully removed already brown needles from the branches of each individual tree. Leaves were oven-dried at 60°C for 48 h, and the dry weight was measured. Total tree biomass was determined at the end of the experiment and separated into needles, wood, and roots (Supplementary Table 1). We separately assessed leaf biomass above and below the sap flow sensor in order to derive total tree transpiration (see section Soil Water Content and Transpiration). As needle elongation was finished before the experiment started, initial leaf biomass per tree was considered as the sum of the remaining needles at the end of the experiment plus leaf biomass shed during the experiment, assuming a constant above-sensor leaf biomass/below-sensor biomass ratio. In order to obtain the actual daily leaf biomass time series, we linearly interpolated cumulative leaf shedding between measurement campaigns and subtracted it from the initial leaf biomass. For each tree, conversion from leaf biomass to leaf area was done based on specific leaf area (SLA, cm2 g−1), obtained by measuring the width and the length of a representative sub-sample per tree (in total n = 18). No significant differences were detected between monitored and not-monitored individuals regarding SLA and tree biomass in different compartments (see Supplementary Table 1).
Xylem Loss in Hydraulic Conductance
We measured xylem vulnerability of branches using the Cavitron technique (Cochard, 2002). Briefly, the centrifugal force of the Cavitron increases the negative pressure in the stem while the hydraulic conductivity and the loss thereof is measured concurrently. At the beginning of the experiment, we sampled the terminal part of the lowest branch (~33 cm long) in five randomly selected non-monitored trees. Branches were tightly wrapped in cling film and additionally sealed in plastic bags before being transported to Innsbruck where they were kept at 4°C for 2 days. Samples were prepared for the Cavitron as follows: first, side twigs and needles were removed, and branches were re-cut under water several times to relax xylem tension, until a sample length of ~28 cm was reached and debarked at both ends (~5 cm) to avoid clogging of tracheids by resin. The cut and debarked ends were cleaned with a sharp razor blade. To remove native embolisms via vacuum infiltration, submerged samples were subjected to a low-pressure water flow (0.08 MPa) for 30 min with distilled, filtered (0.22 μm), and degassed water containing 0.005% (v/v) Micropur. Then, branch segments were fixed into a custom-made, honeycomb 28-cm rotor and positioned in a Sorvall RC-5 centrifuge (Thermo Fisher Scientific, Waltham, MA, United States). Distilled, filtered (0.22-μm pore size), and degassed water with 0.005% (v/v) Micropur water purifier (Katadyn Products, Wallisellen, Switzerland) preventing microbial growth, was used for the measurements. Percent loss of conductivity (PLC, in %) measurements started at a force of about −0.5 MPa, which was gradually increased until minimum xylem hydraulic conductivity (Kxylem, mol m−1 s−1 MPa−1) was reached. PLC was recorded at about −0.5 MPa pressure increase steps. We assumed that losses in conductivity reflect losses in xylem conductance (kxylem, in mol m−2 s−1 MPa−1). In order to model normalized kxylem (knorm, 0–1) responses to xylem water potential increase (Ψxylem), we evaluated three different response functions: a Weibull function (WB), a sigmoid exponential (SE) function, and the original SOX model function (SOXf)
where knorm, WB, knorm, SE, and knorm, SOXf are the predicted normalized kxylem of theWB, SE, and SOXf formulations, respectively. Ψxylem (MPa) is the xylem water potential. In WB, Ψref is the reference xylem water potential (MPa) when knorm, WB is equal to exp(−1) ~0.37. In SE and SOXf, Ψ50 is the xylem water potential at which knorm = 0.5. In all the three formulations, Acoef is a unit-less shaping parameter. See section Xylem Vulnerability for details about the fitting procedure.
Photosynthesis An/Ci Curves
In order to provide estimates for photosynthetic parameters in the FvB model, An/Ci curves were measured on trees grown in the greenhouse in June, 2019. Measurements were made on sun-exposed needles, using a portable infrared gas analyzer system (LI-6800, Li-Cor, Inc., Lincoln, NE, United States) with a 6-cm2 leaf chamber. The measurements were taken at saturating PAR (PAR ≥ 1,200 μmol m−2s−1). Assimilation in relation to [CO2] in the intercellular space (An/Ci) curves was generated by increasing atmospheric CO2 concentration (Ca) inside the chamber in five steps, starting at ~400 μmol mol−1 and then progressively increasing Ca by ~200 μmol mol−1 each step, up to a maximum of ~1,200 μmol mol−1. Leaf temperature (Tleaf, in °C) and other standard variables were also measured. These measurements were taken under prevailing leaf temperature (~25°C) and humidity conditions within the greenhouse. A total of 19 An/Ci curves were measured this way. We used these data to determine carboxylation velocity limited by rubisco activity at 25°C (Vcmax, 25 in μmol m−2 s−1) and the carboxylation velocity limited by RuBP regeneration rate (Jmax,25 in μmol m−2 s−1).
Modeling Approach
The tree hydraulic modeling approach is based on the process-based model SOX (Eller et al., 2018, 2020). We have modified the photosynthetic module, added the possibility to address non-stomatal-limitations of photosynthesis (see below), and included a third conductance node (i.e., the soil-to-root hydraulic conductance, Figure 2). In the following, we refer to the modified model version as the SOX+ model. Briefly, the model operates on the assumption that plants regulate stomatal conductance to maximize photosynthesis, while minimizing the loss in root-to-canopy water conductance. The model is relatively simple in terms of parameterization and computational power required and, hence, applicable for a wide range of ecosystem models. The environmental drivers required as an input to run the model are air temperature, PAR, soil water content, and air relative humidity. Here, we describe the main processes involved such as the modification for SOX+, while a more in-depth description of the original SOX model and the analytical solutions for its equations can be found in Eller et al. (2020).
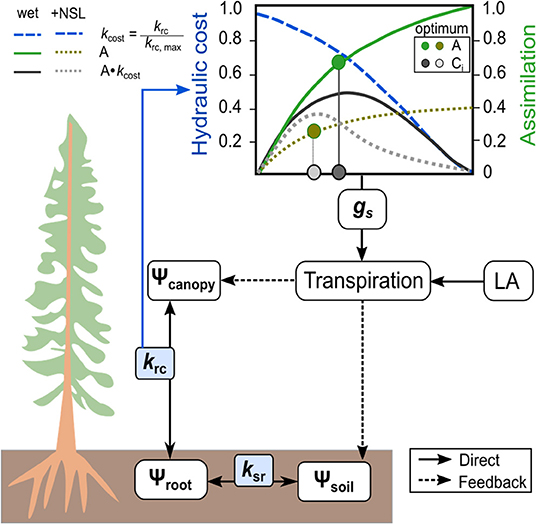
Figure 2. Scheme of the SOX+ model. Soil-to-atmosphere is described as a hydraulic pathway considering three nodes: hydraulic flow from soil to the roots, mediated by soil-to-root conductance (ksr), hydraulic flow from roots to the canopy, mediated by root-to-canopy conductance (krc), and hydraulic flow from the canopy to the atmosphere, mediated by stomatal conductance (gs). The optimum gs is determined by considering the photosynthetic gain (A) multiplied by the hydraulic cost function (kcost), which describes the decreases in krc as Ψcanopy becomes more negative. Transpiration is calculated at the tree level by multiplying gs and leaf area, and it has a direct effect on canopy water potential, an indirect effect on soil water content, and therefore on Ψsoil. Non-stomatal limitations of photosynthesis (NSL) decrease optimum stomatal conductance because of limiting A when Ψcanopy declines below a predefined threshold.
Water flow within the tree is described as a three-step pathway with three different hydraulic conductance nodes: the soil-to-root hydraulic conductance (ksr,mol m−2 s−1MPa−1), the root-to-canopy hydraulic conductance (krc, mol m−2 s−1MPa−1), and the leaf-atmosphere hydraulic conductance (gs, mol m−2 s−1). The model assumes a steady state of tree water status, i.e., it does not account for tree capacitance. The soil-to-root conductance ksr is calculated following Campbell (1985):
where ksr,max is the ksrwhen SWC is at field capacity, SWC is the volumetric soil water content (m3 m−3), SWCFC is the volumetric SWC at field capacity (m3 m−3), and b is an empirical coefficient depending on average soil particle size characteristic, calculated as described in Campbell (1985). Using ksr on the one hand, and transpiration per unit of leaf area (E, mol m−2 s−1) on the other, the model calculates the water potential within the roots (Ψroot, t) based on Darcy's law at hourly time-steps as
where Ψsoil,t is the soil water potential at time step t (in MPa), calculated according to Campbell (1985) from soil physical properties. Canopy water potential (Ψcanopy,t) is closely linked to root water potential, which in turn strongly depends on soil water availability. We assume a simple gravimetrical decline with height, neglecting a potential influence of stored plant water:
where krc(t−1) is the hydraulic conductance from the roots to the canopy at t – 1 (mol m−2 s−1MPa−1) based on the canopy water potential at that time. Therefore, we assume that Ψcanopy, m equals Ψxylem and that krc(Ψcanopy,m) follows the shape of knorm(Ψxylem), multiplied by the maximum root-to-canopy hydraulic conductance (krc, max, in mol m−2s−1 Mpa−1). For representing knorm(Ψxylem), we selected Equation 2, as we found it represented measured data best (see section Leaf Shedding Speed Increased Concurrently With Transpiration Stop). Further, h is the plant height (in m), ρ is the density of water (997 kg m−3), and g is gravity (9.8 m s−2). The 10−6 multiplier transforms Pa to MPa. For each day, we calculated pre-dawn canopy water potential (Ψcanopy, PD, MPa) using equation 7 but assuming E(t−1) ≈ 0, which results in Ψcanopy, PD being dependent on Ψsoil minus the gravimetric component. As in the previous SOX model iterations (Eller et al., 2018, 2020), SOX+ represents the water potential in the xylem with a dampened canopy water potential (Ψcanopy,m, MPa), calculated as for all the hourly calculations to account for the gradual decline in water potential along the plant hydraulic pathway. Such assumption greatly simplifies the calculation of water potential drop within the tree (e.g., Sperry and Love, 2015; Sperry et al., 2017).
The core assumption in SOX+ is that stomatal conductance (gs, mol m−2 s−1) is regulated to maximize photosynthetic net assimilation (An, μmol m−2 s−1) while minimizing the decrease in xylem hydraulic conductance, represented by root-to-canopy conductance (krc) here. Eller et al. (2020) solved for gs using an analytical approximation based on the partial derivatives of An with respect to CO2 concentration in the chloroplast (Ci, μmol mol−1) and krc with respect to Ψcanopy,m.
where δAn/δCi represents the gain in net photosynthesis per unit of Ci increase, i.e., the positive effect of opening the stomata on An, solved numerically as in Eller et al. (2020), while ξ represents the cost in terms of loss in hydraulic conductance of opening the stomata as canopy water potential declines and/or vapor pressure deficit increases (Equation 9). Specifically, the lower the ξ, the lower the stomatal conductance projected by SOX+. If estimates of gsSOX are lower than a predefined minimum leaf conductance, representing leaf leakiness once stomata are fully closed (gmin, in mmol m−2 s−1; here 2 mmol m−2 s−1), we considered gs equal to gmin, otherwise gs = gsSOX, following Duursma et al. (2019). Note that in the approach, gmin integrates leaf water losses both because of imperfect stomatal closure and leaf cuticular conductance, considering a well-coupled canopy and low wind speed conditions (e.g., Cochard et al., 2021).
where VPD is the vapor pressure deficit at leaf level (kPa) and represents the decrease in conductance as mean canopy water potential increases, solved numerically as described in Eller et al. (2020). rplant, min is the minimum plant resistance (in MPa m2 s mol−2), a parameter used to describe the increase in whole tree resistance with decreasing Ψcanopy,m.
Net assimilation (An) is calculated according to the Farquhar, von Caemmerer, and Bell photosynthesis model (FvCB, Farquhar et al., 1980; De Pury and Farquhar, 1997). Briefly, the FvCB assumes that An is limited by either rubisco carboxylation velocity (Avc) or RuBP regeneration (Aj), and is calculated considering dark respiration (Rd). All of these processes depend on leaf temperature (Farquhar et al., 1980; Harley et al., 1992; Bernacchi et al., 2001), which we assume to equal air temperature.
As novelty compared with the original SOX model, SOX+ accounts for non-stomatal limitations (NSL) in photosynthesis, as have been repeatedly found important to properly represent reductions of transpiration and productivity under drought stress (e.g., Keenan et al., 2010; Duursma and Medlyn, 2012; Drake et al., 2017; Yang et al., 2019, Gourlez de la Motte et al., 2020). NSL assume that additional constrains on An arise with decreasing Ψcanopy from mesophyll conductance reductions, biochemical limitations, or other indirect effects (e.g., Fatichi et al., 2014). Here, note that in SOX+ and according to Equation 8, NSL will result in a reduction in δAn/δCi, thus also indirectly leading to reduced gsSOX. In SOX+, declining Ψcanopy,m[f (Ψcanopy,m), unit-less, its value ranging between 1 (no limitation) and 0 (complete limitation)] is calculated based on Tuzet et al. (2003) as follows:
where Ψref,Tuz and aTuz are two empirically determined parameters, Ψref,Tuz being a reference canopy water potential (in MPa), as defined in Tuzet et al. (2003), and aTuz being a unit-less coefficient that determines the sensitivity of the sigmoid curve to Ψcanopy,mreductions. After simulating f (Ψcanopy,m), apparent Vcmax and apparent Jmax are computed as
where the Xapparent (μmol m−2 s−1) is the apparent kinetic parameter value for either Vcmax or Jmax for a Xmax,25 (μmol m−2 s−1) reference value (see Table 2) multiplied by the NSL (Equation 12), represented by the unit-less stress term f (Ψcanopy,m). These new kinetic parameters accounting for direct impacts of Ψcanopy decline on photosynthesis are then used to calculate Avc and Aj in Equation 11.
Because of the feedback mechanism between An and gs, SOX+ solves both processes iteratively for the equilibrium Ci.
Model Parameterization and Calibration
Photosynthesis in the FvCB Model
Temperature dependencies of rubisco kinetics were obtained from Bernacchi et al. (2001). Temperature dependencies for the FvCB model were obtained for P. sylvestris from Wang et al. (1996), see Table 1 for the parameter values. To obtain the carboxylation velocity limited by rubisco activity at 25°C (Vcmax, 25 in μmol m−2 s−1) and the carboxylation velocity limited by RuBP regeneration rate (Jmax,25 in μmol m−2 s−1), we used measured An/Ci curves under no drought stress to calibrate the FvCB model for each curve individually, using the package “DEOptim” (Mullen et al., 2011). The algorithm obtains the most likely parameters providing the observations, a parameter distribution and a likelihood function, by performing differential evolution optimization (see below for more details). We used the default three-chain settings to establish non-informative priors within the biological meaningful range (Table 2). The objective function for optimization was a Gaussian log-likelihood distribution. This provided a Vcmax, 25 and a Jmax, k25 value for each curve. To summarize the average photosynthesis kinetics of the P. sylvestris population, we used the median calibrated values of Vcmax, 25 and Jmax,25 to run the SOX+ model (Table 2). We calculated the dark respiration rate at 25°C (Rd, 25 in μmol m−2 s−1) as Rd, 25 = 0.015*Vcmax, 25, according to Collatz et al. (1991). After FvCB model optimization, Anestimates were very close to observations [Figure 3, slope not significantly different than 1(p > 0.1) and intercept not significantly different than zero (p > 0.1)]. The median Jmax,25 to Vcmax, 25 ratio was ~1.7, with Vcmax, 25 values of 33.3[27.7–38.9] μmol m−2 s−1 (median [95% CI]), and Jmax,25 values of 51[45.1–56.8] μmol m−2 s−1 (Table 2). To run the SOX+ model, we used the median values of Vcmax, 25 and Jmax,25.
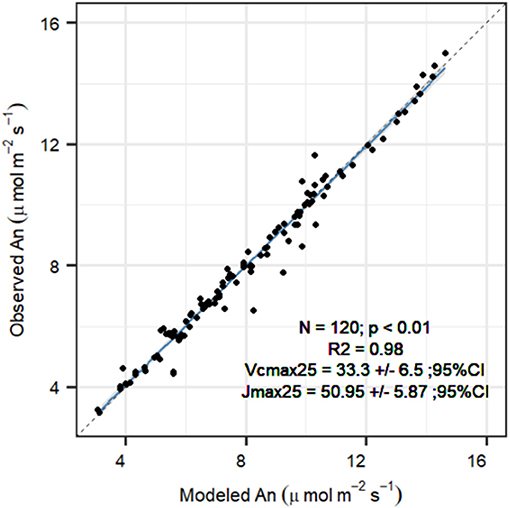
Figure 3. Comparison between FvCB model net assimilation (An, μmol m−2 s−1) projections with observations after parameter optimization for each An/Ci curve (n = 19), for the P. sylvestris saplings grown in the greenhouse in year 2019. Reported are the fit (R2), the median optimum Vcmax,25 ± 95% confidence interval, and the median optimum Jmax,25 ± 95% confidence interval. The solid line indicates the trend between observed and modeled An (p < 0.01), with the gray area representing the 95% CI. The slope was not significantly different than 1 (p > 0.1), and intercept was not significantly different than 0 (p > 0.1) based on a t-test. Dashed line represents the 1:1 fit.
Xylem Vulnerability
In order to decide for an appropriate response function and define the respective parameters describing kxylem(Ψxylem), we first inversely calibrated each of the proposed equations (Equations 2–4) with the kxylem(Ψxylem) observations. Independent of the equation we proceeded as follows: we calibrated one vulnerability curve per sample using each of the three equations, using broadly set but biologically meaningful priors (Table 2) and a Gaussian likelihood function. The sampler used was a differential evolution Markov Monte-Carlo Chain (MCMC) with memory and a snooker update (DEzs, terBraak and Vrugt, 2008), implemented in the “BayesianTools” R package (Hartig et al., 2017). We ran each calibration for 50 k iterations, and then the first 30 k where discarded as a burn-in. For initial trials, we ran tree calibrations for each vulnerability curve and addressed between-chain convergence via Gelman-Rubin convergence diagnosis (Gelman and Rubin, 1992). As running the model this way is time-consuming and the initial trials provided very low Gelman–Rubin scores for all the three equations (G-R < 1.02, n = 2 for each model), which indicates fast convergence, we visually inspected the MCMC to confirm convergence afterward. Once all individual curves were calibrated, we merged the five posteriors to obtain the average response by sampling with replacement 1 k times the posterior distribution for each curve. We then merged the samples together into a new combined posterior distribution. From this combined posterior distribution, we obtained the median parameter value ±95% confidence intervals. Model predictions were performed by sampling 1 k samples from the combined posterior. Goodness of fit was assessed for each run through the root mean square error (RMSE) and a pseudo-R2 calculated from Spearman's correlation coefficient as pseudo-R2 = [cor (Observed, Modeled)]2. Finally, SOX+ was run with the median parameters of the equation that presented the best fit (i.e., the Weibull equation, Equation 2).
SOX+ Model
We calibrated the SOX+ model based on average daily transpiration rates of the tree population (n = 6). To do so, we performed Bayesian inverse model calibration (e.g., Ellison, 2004; Hartig et al., 2012) selecting the parameters ksr,max, krc,max, rplantmin, Ψref,Tuz, and aTuz. Since we were primarily interested in the initial transpiration response to decreasing soil water content to see if SOX+ was able to capture the dry-down phase, we only used the initial 19 days (DOY 212–230) for calibration, further excluding days 216 and 217 because of low VPD and PAR conditions in the greenhouse (Figure 1). As including or not a given process changes the whole structure of the model, and because we wanted to run SOX+ with and without accounting for NSL, we performed two different calibrations (hereafter referred as “Hydraulic,” i.e., SOX + model without including NSL, and “Hydraulic+NSL,” i.e., SOX + model including NSL). The procedure was the same in both cases, though the “Hydraulic” calibration did not include the Ψref,Tuzand aTuz parameters. Again, we used broadly set, biologically meaningful priors (Table 2), a Gaussian likelihood function, and the differential evolution MCMC with memory and a snooker update (DEzs, terBraak and Vrugt, 2008) as implemented in the “BayesianTools” R package (Hartig et al., 2017). We ran each calibration three times, 30 k iterations each, and then we discarded the first 20 k iterations as a burn-in. Between-MCMC convergence was addressed by the Gelman–Rubin convergence diagnosis (G-R <1.1 for both calibrations, G-R <1.1 considered being a conservative threshold; Brooks and Gelman, 1998). To assess the calibrated SOX+ performance, we ran for 500 times both the “Hydraulic” and “Hydraulic+NSL” model formulations for the entire time series (DOY 212–265), by sampling resulting posterior parameter distribution. For each run, we compared projected daily cumulated transpiration with the observations using a linear model accounting for temporal autocorrelation with an auto-regressive [corAR()] correlation structure centered in DOY. This was done with the package “nlme” (Pinheiro et al., 2021). Goodness of fit was assessed through the RMSE and a pseudo-R2 [; Cox and Snell, 1989), based on the deviance from the regressive model with respect to the null model and reported as the median RMSE and for the 500 runs.
Simulation Scenarios
NSL and Leaf Shedding Importance in Preventing Loss in Hydraulic Conductance
To quantify the importance of non-stomatal limitations (NSL) of photosynthesis and leaf shedding in preventing krc decline, we ran the calibrated SOX+model for 54 days (DOYs 212–265) under the following scenarios: (1) hydraulic limitations with observed leaf shedding dynamics, i.e., accounting for the daily leaf area reduction (Hydraulic scenario, ran with the “Hydraulic” calibration); (2) Hydraulic limitations and NSL, but considering leaf area constant at the initial value during the entire simulation (Hydraulic + NSL scenario, ran with the “Hydraulic+NSL” calibration); and (3) Hydraulic limitations and NSL plus observed leaf shedding dynamics (Hydraulic + NSL + leaf shedding scenario, ran with the “Hydraulic+NSL” calibration). This setup enabled to assess the importance of NSL and leaf shedding on krcloss separately. To obtain model projections for each scenario, we sampled 500 times the posterior parameter distribution. We report the daily evolution of percent loss in krc(PLkrc, in %), calculated as 100*krc(Ψcanopy, PD)/krc, max, as the median ± 95% CI of the 500 runs.
Importance of Leaf Shedding at Different Degrees of Leaf Leakiness
We tested the sensitivity of the model to variations in minimum leaf conductance (gmin). This highly uncertain parameter is assumed to vary strongly between plants, while being extremely important for water loss and leaf shedding under extreme drought stress (e.g., Vilagrosa et al., 2003; Hochberg et al., 2017; Duursma et al., 2019; Li et al., 2020). It is assumed that plants with higher gmin will likely benefit more from leaf shedding, as the reduction in water loss per unit of leaf shed will be higher. The model formulation “Hydraulic+NSL” was run with two different gmin values (gmin = 2 mmol m−2 s−1 and gmin = 3 mmol m−2 s−1, a 50% increase), considering either constant leaf area, i.e., no leaf shedding, or observed leaf dynamics, i.e., observed leaf shedding. Again, posterior parameter sampling with replacement was carried out for 500 model runs for each of the 2 × 2 scenarios (leaf dynamics × gmin assumption). Then, for each gmin scenario, we calculated the daily average cumulative benefits of leaf shedding as
where BenefitLS,i is the daily average cumulative reduction in percent loss of krc if trees dynamically shed their leaves relative to the same trees in the absence of leaf shedding, “i” is the day since the beginning of the experiment, and PLkrc,NoShed,i and PLkrc,Shed,i are the percent loss in krc on day “i” in the absence or presence of leaf shedding, respectively. For this and all the other statistical analyses described before, as well as to develop and implement the SOX+ model, we used the R statistical program (R Core Team, 2021, Version 3.6.1).
Results
Calibration of Xylem Vulnerability Models
All the three equations to describe hydraulic vulnerability [Weibull (WB); sigmoid exponential (SE), and original SOX+ formulation (SOXf)] provided similar, overlapping results. The median xylem water potentials at which 50% of loss in hydraulic conductivity occurred were: WB −2.53 MPa, SE −2.6 MPa, and SOXf−2.6 MPa. The WB function described the observed trends slightly better than the other functions while also maintaining the assumption in the original SOX model that loss of hydraulic conductivity does not occur at Ψxylem values ≈ 0 (Figure 4). Therefore, WB was selected to run SOX+ for P. sylvestris in this experiment. Parameter values describing prior and the posterior parameters are listed in Table 2.
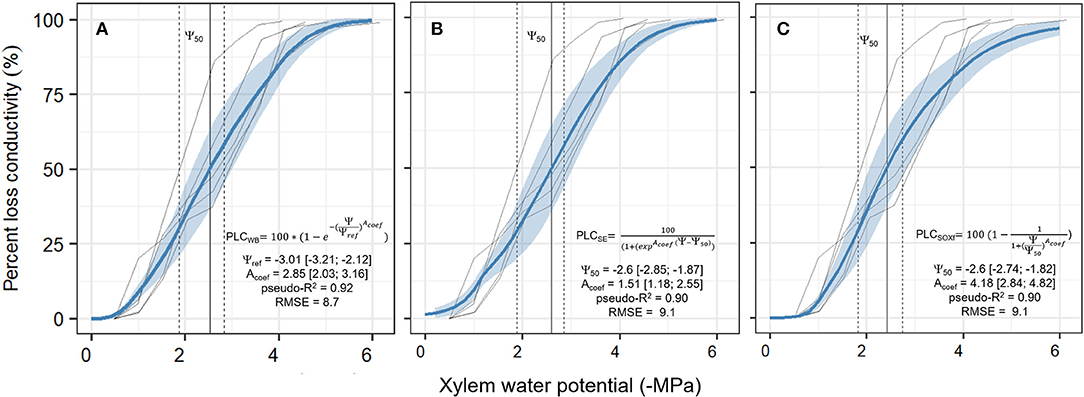
Figure 4. Calibration of the three different xylem vulnerability models [Weibull model (WB, A), the Sigmoid Exponential (SE, B), and the original SOX formulation (SOXf, C)] for the P. sylvestris saplings. Solid transparent lines are the five measured curves of the observed percent loss in xylem conductivity (PLC, in %) in relation to xylem water potential decrease (Ψxylem, in -MPa). Solid blue line ± shadowed blue area is the median ± 95 CI obtained from 1 k model runs sampling the combined posterior parameter estimate, resulting from curve-individual calibrations for each model, as described in section Xylem Vulnerability. The vertical solid line shows the Ψ50 value; this is when xylem has lost 50% of its conductivity (±95% CI, vertical dashed lines). For each model, formulation and median ± 95% CI values for each parameter are provided. Note that in the WB model Ψref parameter meaning is not equivalent to the Ψ50 parameter from the other two models. Goodness of fit is given as the median pseudo-R2 and the median root mean square error (RMSE) of all model runs.
Leaf Shedding Speed Increased Concurrently With Transpiration Stop
After starting the drought experiment at DOY 212, transpiration of all six measured P. sylvestris saplings decreased from 1–2.6 kg tree−1 day−1 to about 10% of the starting value within 2 weeks (DOY 226). Within this period, transpiration was strongly reduced for 2 days (DOY 216–217), most likely because of exceptionally cloudy days with low temperature conditions outside the greenhouse that were not compensated (see Supplementary Figure 2). From DOY 227 onward, tree transpiration almost stopped, with median [95% CI] values of 0.034 [0.001–0.19] kg tree−1 day−1 (Figure 5). At the same time, leaf shedding increased, which was only marginal during the initial phase of the experiment (0.2 [0.02–0.2] % day−1 between DOY 212 and 225). Once transpiration was close to zero, litterfall tripled to 0.55[0.03–0.9] % day−1. At the end of the experiment (DOY 265), the trees had lost 30.2% [16.9–37.8] of the initial leaves. We observed that only 2 and 3 year-old needles were shed but never current year needles.
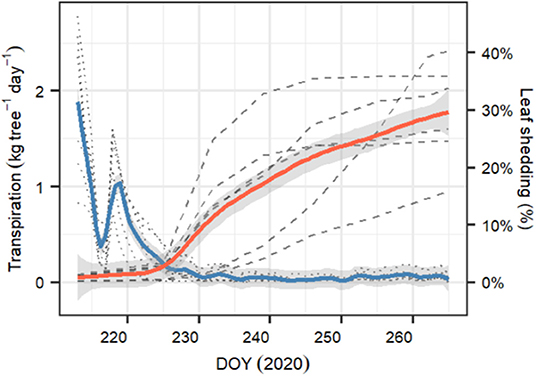
Figure 5. Temporal evolution of whole-tree transpiration (in kg tree−1 day−1) and percent of leaf shed for the six monitored P. sylvestris saplings growing in the greenhouse during the whole length of the experiment (DOY 212–265). Blue line represents the average daily transpiration ±1 SD, whereas red line represents the daily cumulated percent of leaf shed since the beginning of the experiment ±1 SD. Transparent dotted lines are the observed daily transpiration for each tree, and transparent dashed lines are the cumulated percent of leaf shed for each tree.
SOX+ Performance Improved When Including Non-Stomatal Limitations of Photosynthesis
SOX+ model calibration accounting for non-stomatal limitations (Hydraulic + NSL) outperformed the standard SOX+ model (Figure 6) during the entire experiment. It also provided a more realistic set of posterior parameter estimates, especially regarding ksr,max (Table 2). For the calibration period (DOY 212–230), the standard “Hydraulic” model setup led to 27.8 ± 17% (Median ± SE) overestimation of daily transpiration, while with “Hydraulic+NSL,” the error reduced to 2.5 ± 16.9% (Figure 6C). Such differences were especially important during the dry-down phase (DOY 220–228). The differences in accuracy between the two model simulations strongly declined during the second half of the experiment, when both model setups resulted in full stomatal closure (gs = gmin, DOY 240–265).
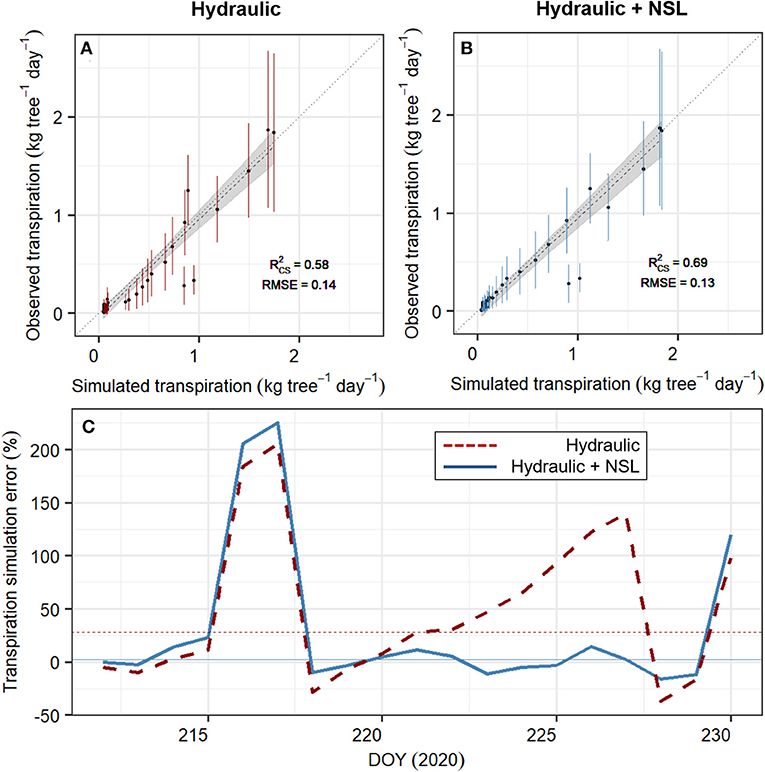
Figure 6. Performance of the SOX+ model calibrated without (“Hydraulic,” A, in red) and with (“Hydraulic + NSL,” B, in blue) non-stomatal limitations of photosynthesis. (A,B) show the comparison between simulated and observed transpiration (in kg tree−1day−1, points ± SD error bars), during the experiment (DOY 212–265). Daily simulated transpiration is the projected median by sampling 500 times each of the SOX+ model formulation posterior parameter estimates. Noted is the generalized linear model accounting for temporal autocorrelation, model fit (), and the RMSE. In both formulations, the slope was not significantly different than 1 (p < 0.01), and the intercept was not significantly different than 0 (p < 0.01). (C) represents the SOX+ error in transpiration estimates for the calibration period (DOY 212–230), and for the Hydraulic (red, dashed lines) and Hydraulic + NSL (blue, continuous lines) formulations. Simulation error was calculated as , where Trsim is the daily median transpiration from the 500 model, and Trobs is the daily observed transpiration, both in kg tree−1 day−1. Horizontal lines represent the median simulated error for each SOX+ formulation.
NSL and Leaf Shedding Reduce Projected Loss in Root-To-Canopy Hydraulic Conductance
Compared to the original “Hydraulic” SOX+ setup, projected percent loss in root-to-canopy conductance (PLkrc, in %) at the end of the experiment when accounting for NSL (Hydraulic + NSL) was smaller by 6.3 ± 0.2%. Including observed leaf shedding (Hydraulic + NSL + leaf shedding scenario) further reduced projected PLkrc by a 13 ± 0.2 % (Figure 7). Interestingly, with NSL and leaf shedding considered, the median simulated PLkrcafter 54 days of water shortage was below 80%, an important threshold for pine mortality (Hammond et al., 2019). Leaf shedding speed drastically increased between DOYs 225 and 231, when trees had lost between 44 and 53% of their root-to-canopy conductance, according to the SOX+ model (Figure 8) and their stomata were fully closed (daily maximum gs <10% of maximum simulated gs). After full stomatal closure, tree water losses were highly dependent on leaf leakiness, here summarized as gmin. Increasing gmin by 50% resulted in shedding of leaves that was significantly beneficial in reducing krc losses compared with no shedding leaves 6 days earlier than assuming gmin = 2 mmol m−2 s−1 (DOY 244 vs. DOY 250). The benefits of leaf shedding were significantly higher at gmin = 3 mmol m−2 s−1 than at gmin = 2 mmol m−2 s−1 after DOY 232 (p < 0.05, after a Kolmogorov–Smirnov non-parametric test), and for the rest of the period simulated (Figure 9).
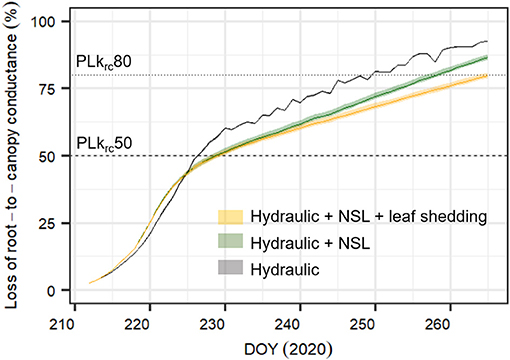
Figure 7. Simulated percent loss in root-to-canopy conductance during the experiment (PLkrc, in %) with three different SOX+ model formulations. Only hydraulic constraints on stomatal conductance (Hydraulic, in gray); hydraulic constrains on stomatal conductance and non-stomatal limitations of photosynthesis accounting for equal leaf area during the whole experiment (Hydraulic + NSL, in green); and hydraulic constraints on stomatal conductance, non-stomatal limitations of photosynthesis, and observed leaf shedding (Hydraulic + NSL + leaf shedding, in orange). Posterior parameter distributions are different for (Hydraulic) and (Hydraulic + NSL, Hydraulic + NSL + leaf shedding), see Table 2. For each model formulation, the figure shows the daily pre-dawn median ± 95% CI PLkrc, obtained from running the simulation by sampling 500 times the posterior parameter distribution. Horizontal lines indicate when krc = 0.5 * krc,max (PLkrc50, dashed line), and when krc = 0.2 * krc,max (PLkrc80, dotted line), a threshold that has been found to be critical for pine survival probability (Hammond et al., 2019).
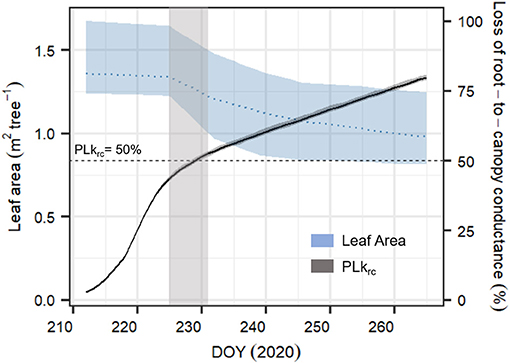
Figure 8. Time series of averaged leaf area (in m2 tree−1, blue dashed line) for the six monitored Pinus sylvestris saplings and simulated dynamics in percent loss in root-to-canopy conductance (PLkrc, in %, black continuous line) according to the complete SOX+ model scheme (Hydraulic + NSL + leaf shedding). Daily leaf area is represented as the mean ± SD. Daily simulated PLkrc is represented as the median ± 95% CI after 500 model simulation runs by sampling the posterior parameter estimate. The horizontal line indicates when krc = 0.5 * krc, max (PLkrc50, dashed line), while the light gray area represents the uncertainty of when the leaf shedding rate accelerated. Because of weekly sampling campaigns, the area is relatively broad.
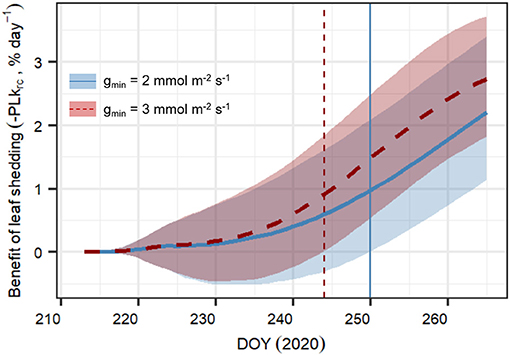
Figure 9. Daily averaged cumulated benefit of observed leaf shedding in preventing loss in root-to-canopy conductance (PLkrc, in %) for minimum leaf conductance (gmin) = 2 mmol m−2 s−1 (blue continuous line), and gmin = 3 mmol m−2 s−1 (red dashed line). Results represent the median ± 95% CI of 500 model simulations obtained by randomly sampling the posterior parameter distribution for each of the following scenarios and their combination:with and without leaf shedding, and the two gmin values considered. The daily average cumulated difference in PLkrc between shedding and no shedding is calculated according to Equation 14. The vertical lines for both scenarios indicate the DOY at which the benefit of leaf shedding is significantly >0.
Discussion
The findings suggest that non-stomatal limitations (NSL) of photosynthesis and leaf shedding processes play an important role as hydraulic safety mechanisms in P. sylvestris, as they reduce losses in root-to-canopy conductance during severe drought stress (Figure 7). Drought-induced leaf shedding in P. sylvestris saplings started when predicted loss of root-to-canopy hydraulic conductance was close to 50%. This is in accordance with the “hydraulic fuse” hypothesis, which states that cavitation in leaves would occur earlier than xylem cavitation to avoid irreversible xylem conductance losses (e.g., Hochberg et al., 2017, Choat et al., 2018), as leaves are cheaper to rebuild than new vessels in the xylem (Tyree and Ewers, 1991). The results also concur with previous observations of leaf shedding delaying the time to reach lethal dehydration thresholds (Blackman et al., 2019) while also identifying gmin as a key trait involved in plant dehydration processes (Duursma et al., 2019; Cochard, 2020). These findings highlight the importance of including non-stomatal processes (i.e., NSL and leaf area adjustments) into simulation models in order to account for tree physiological feedback responses to drought stress.
Non-Stomatal Limitations of Photosynthesis as a Hydraulic Safety Mechanism
Including NSL to restrict photosynthesis improved the SOX+ model representation of observed transpiration reductions during the dehydration phase, especially when stomata were not fully closed. Model improvements based on similar observations have been reported previously (e.g., Yang et al., 2019; Gourlez de la Motte et al., 2020). Including NSL reduced projected losses in root-to-canopy conductance by overall 6% after 54 days without irrigation. It also delayed reaching 80% of PLkrc, an important threshold for pine mortality (Hammond et al., 2019), by 8 days. As plants dehydrate, considering NSL led to lower optimum stomatal conductance per photosynthetic gain (i.e., it led to decreased δAn/δCi in Equation 8). We identified a Ψcanopy reference value of −1.7 MPa for a 50% strength of the NSL limitation, this value being lower than the observed Ψxylem, 50 (−2.6 MPa). This implies that NSL mechanisms are acting at the onset of embolism formation, which may be indicative of an active hydraulic safety mechanism (Choat et al., 2018).
We acknowledge that simulating NSL as a decline in apparent Vcmax and Jmax summarizes the effects from a multiplicity of interacting plant physiological responses to drought, which might be better considered separately. For example, water and carbon transport in the mesophyll might be described as a function of aquaporin expression in dependence on cell water potential (Flexas et al., 2012; Paudel et al., 2019), and the effects on photosynthesis could be separated into suppression of rubisco regeneration (Rizhsky et al., 2002; Pilon et al., 2018), and reduction in rubisco activity. Also, reduced sink strength of tissue experiencing drought limitations (Hsiao et al., 1976; Fatichi et al., 2014) could eventually be used to describe the down-regulation of photosynthesis explicitly, e.g., via higher leaf sugar concentration due to reduced phloem load (Riesmeier et al., 1994; Sevanto, 2014). These mechanisms, however, have not been sufficiently resolved to be used in general models.
Shedding Leaves After Stomatal Closure Buffered Projected Loss in Conductance
Reducing leaf area is a well-known phenomenon that decreases whole tree transpiration (e.g., Whitehead et al., 1984; Martínez-Vilalta et al., 2014; Wolfe et al., 2016). During the first phase of the dry-down, leaf shedding was only marginal, but it increased after full stomatal closure (Figures 5, 8), when reducing leaf area was the only possibility to further reduce leaf leakiness and leaf C maintenance cost. We found that leaf shedding reduced projected krs losses by 7% at the end of the experiment. Also, when including leaf shedding dynamics, the pines did not reach the lethal PLkrc80 threshold. Interestingly, increasing gmin by 50% further underscored the benefits of leaf shedding, which then even started earlier during the dry-down. Since gmin seems to depend on environmental conditions during leaf development (Duursma et al., 2019) and also increases with leaf temperature (e.g., Schuster et al., 2016; Cochard, 2020), leaf shedding may represent an acclimation strategy to counteract leaf leakiness during later growth stages (Blackman et al., 2019) and heat waves. This is supported by findings that less sclerophyllous trees (i.e., those with higher gmin) are likely to shed more leaves earlier during heat-drought stress development (e.g., Ogaya and Penuelas, 2004; Montserrat-Marti et al., 2009).
In accordance with recent findings (Wolfe et al., 2016; Cardoso et al., 2020; Li et al., 2020), Scots pine shed its 2 and 3 year-old needles once krs was halved and leaf conductance was strongly reduced (approximately gs = gmin). This implies that in P. sylvestris, leaf shedding has likely been triggered as a last-chance hydraulic safety mechanism, as pines do not re-grow shed leaves until the next growing season. This may lead to severe C uptake reductions after drought release, especially if the drought occurs early during the growing season (Eilmann et al., 2013), with consequences that may extend up to 4 years after drought (e.g., Galiano et al., 2011). In the experiment, the trees shed about 30% of their leaves, which may imply an equivalent loss in photosynthesis capacity after re-watering. Such C uptake reductions may still have severe implications for post-drought xylem and canopy recovery (e.g., Yan et al., 2017; Ruehr et al., 2019; Kannenberg et al., 2020). However, negative impacts of leaf losses are probably less severe because mostly the older leaves, which are less efficient in terms of photosynthesis, were shed first (Escudero and Mediavilla, 2003; Niinemets et al., 2005, but see Poyatos et al., 2013). Also, the C balance during drought is less negative because of reduced maintenance respiration; thus, lower depletion of non-structural carbohydrates reserves is expected. The inclusion of the SOX+ model in a whole-tree dynamics simulation model may shed more light upon the benefits and drawbacks of leaf shedding in terms of whole tree C balance and growth.
Uncertainties and Lines to Proceed Further
Trees may respond to soil drought with various physiological reactions in order to save water and protect their conductive tissue. Besides stomatal regulation of evaporation demand and potential photosynthesis, additional processes are involved that affect the relationship between stomatal opening and photosynthesis activity, particularly under drought as has been described, e.g., by Eller et al. (2018, 2020). In this study, we have accounted for these processes in a lumped way by training a process-based tree hydraulic model (SOX+) from “in situ” observations (e.g., Medlyn et al., 2015; Dietze et al., 2018). However, we acknowledge that the experimental basis for this new mechanism is still poor, based on a small number of repetitions and a relatively high variability in individual plants. Also, it would be more convincing that loss in xylem conductance is a driving force for drought responses if it would have been directly measured instead of indirectly calculated from water potential and transpiration. It should also be noted that the additional parameters required to describe the new model features are yet uncertain with respect to their generality; thus, further studies are needed to evaluate their precision, species-dependency, or relationship to wood or leaf anatomical traits (Schumann et al., 2019, Velikova et al., 2020).
Similar caution needs to be applied to the second investigated process of leaf shedding. It seems that there is a clear threshold of loss in root-to-canopy hydraulic conductance at which leaf shedding began. Therefore, we suggest a generalization of drought-induced leaf shedding dynamics that may be included in simulation models accounting for tree hydraulics. This is based on a basal leaf turnover rate and a drought-induced leaf shedding rate that is considered after a given threshold of loss in hydraulic conductanceis reached:
where LAi is the whole tree leaf area on day “i” (in m2 tree−1), basalLS is the basal rate of leaf shedding without drought stress, droughtLS is the leaf shedding rate under drought stress, and x is the threshold of conductance loss at which drought-induced leaf shedding occurs. For instance, in the experiment (Section Leaf Shedding Speed Increased Concurrently With Transpiration Stop), basalLS would equal to 0.002, droughtLS to 0.0055, and x to 50%. According to recent observations, 50% loss in hydraulic conductance seems to be a realistic threshold, occurring within a wide range of environments and plant types (e.g., Wolfe et al., 2016; Cardoso et al., 2020; Li et al., 2020). Nonetheless, we acknowledge that depending on the species-specific strategies to face hydraulic stress, such threshold may vary (e.g., Ruehr et al., 2016). We hypothesize further that this strategy may be linked to differences in gmin, as the benefits of leaf shedding appear earlier and to a larger degree when leaf leakiness is higher.
The suggested model modifications account for non-stomatal acclimation mechanisms affecting canopy conductance, which are commonly accepted as an important driver of plant water use regulation but are still poorly tested in simulation models. Nevertheless, we are aware that other potential acclimation processes such as changes in rooting depth, root distribution, or soil-to-root conductance (e.g., Mu et al., 2021), as well as changes in leaf distribution or traits, such as leaf thickness and stomatal density, affect whole plant conductance. Also, short-term responses, such as an increase in leaf cuticular conductance (gmin) in response to rising temperature (e.g., Cochard et al., 2021), are not addressed in this version of SOX+, which leaves room for model improvement. Furthermore, the SOX+ model has, so far, been tested only for small trees growing under controlled conditions. Thus, model performance should be assessed under field conditions, particularly for trees of different sizes and species. Still, the inclusion of NSL and leaf shedding processes enhanced model transpiration estimates, which were identified as key mechanisms that trees trigger to buffer conductance losses under drought stress.
Relevance for Climate-Change Scenario Analyses
Including the proposed processes into ecosystem models would improve water consumption estimates during drought and hot drought events. Because heat waves alongside increased VPD are supposed to increase in intensity and frequency (Basarin et al., 2020), this may potentially improve model projections of forest drought responses. Parametrizing species in order to consider tradeoffs between elongating carbon gain and reducing hydraulic stress via leaf shedding will also enable to better represent the differences in competition strength between tree species under future environmental conditions. This is particularly useful in ecosystem models addressing the interactive impacts of increased atmospheric CO2 and a hotter and drier climate on forests. In addition, the mechanistic simulation of loss in xylem conductance also considering feedback responses may lead to an improvement in tree mortality process description (Bugmann et al., 2019). In contrast to empirical approaches, it allows to consider species- and environmental-specific adaptation strategies, represented by species traits that indicate different hydraulic vulnerabilities. Since tree mortality is an underrepresented but highly important process when addressing forest dynamics under global warming (Meir et al., 2015), incorporating leaf area acclimation to drought and non-stomatal limitations of photosynthesis in larger-scale forest simulation models will likely improve climate change scenario assessments.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: Code and data available at: https://zenodo.org/badge/latestdoi/381126647.
Author Contributions
DN-S wrote the initial version of the manuscript, implemented SOX+ model formulation, and analyzed the data. DN-S, NR, and BB designed and implemented the experiment. RG and NR assisted with manuscript writing and research design and supervised the data analysis. TK analyzed the xylem vulnerability curves. BB, TK, RR, and SS collaborated for the manuscript content and collected field data. All the authors contributed to manuscript editing and writing.
Funding
This study was supported by the German Research Foundation through its Emmy Noether Program (RU 1657/2-1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank Andreas Gast and Martha Lutzenberger for their helpful assistance during the experiment. We also would like to thank the three reviewers for their insightful comments on a previous version of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2021.715127/full#supplementary-material
References
Allen, C. D., Breshears, D. D., and McDowell, N. G. (2015). On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 6, 1–55. doi: 10.1890/ES15-00203.1
Anderegg, W. R., Berry, J. A., Smith, D. D., Sperry, J. S., Anderegg, L. D., and Field, C. B. (2012). The roles of hydraulic and carbon stress in a widespread climate-induced forest die-off. Proc. Nat. Acad. Sci. 109, 233–237. doi: 10.1073/pnas.1107891109
Basarin, B., Lukić, T., and Matzarakis, A. (2020). Review of biometeorology of heatwaves and warm extremes in Europe. Atmosphere 11:1276. doi: 10.3390/atmos11121276
Bassiouni, M., and Vico, G. (2021). Parsimony versus predictive and functional performance of three stomatal optimization principles in a big-leaf framework. New Phytol. 228, 1796–1810. doi: 10.1111/nph.17392
Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, A. R. Jr., and Long, S. P. (2001). Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant Cell Environ. 24, 253–259. doi: 10.1111/j.1365-3040.2001.00668.x
Blackman, C. J., Li, X., Choat, B., Rymer, P. D., De Kauwe, M. G., Duursma, R. A., et al. (2019). Desiccation time during drought is highly predictable across species of Eucalyptus from contrasting climates. New Phytol. 224, 632–643. doi: 10.1111/nph.16042
Blackman, C. J., Pfautsch, S., Choat, B., Delzon, S., Gleason, S. M., and Duursma, R. A. (2016). Toward an index of desiccation time to tree mortality under drought. Plant Cell Environ. 39, 2342–2345. doi: 10.1111/pce.12758
Brodribb, T. J., Powers, J., Cochard, H., and Choat, B. (2020). Hanging by a thread? For. Drought. Sci. 368, 261–266. doi: 10.1126/science.aat7631
Brooks, S. P., and Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat. 7, 434–455. doi: 10.1080/10618600.1998.10474787
Bugmann, H., Seidl, R., Hartig, F., Bohn, F., Bruna, J., Cailleret, M., et al. (2019). Tree mortality submodels drive simulated long-term forest dynamics: assessing 15 models from the stand to global scale. Ecosphere 10:e02616. doi: 10.1002/ecs2.2616
Campbell, G. S. (1985). Soil Physics With BASIC: Transport Models for Soil-Plant Systems. Amsterdam: Elsevier.
Cardoso, A. A., Batz, T. A., and McAdam, S. A. (2020). Xylem embolism resistance determines leaf mortality during drought in Persea americana. Plant Physiol. 182, 547–554. doi: 10.1104/pp.19.00585
Carnicer, J., Coll, M., Ninyerola, M., Pons, X., Sanchez, G., and Penuelas, J. (2011). Widespread crown condition decline, food web disruption, and amplified tree mortality with increased climate change-type drought. Proc. Nat. Acad. Sci. 108, 1474–1478. doi: 10.1073/pnas.1010070108
Chen, D., Wang, S., Xiong, B., Cao, B., and Deng, X. (2015). Carbon/nitrogen imbalance associated with drought-induced leaf senescence in Sorghum bicolor. PLoS ONE 10:e0137026. doi: 10.1371/journal.pone.0137026
Choat, B., Brodribb, T. J., Brodersen, C. R., Duursma, R. A., Lopez, R., and Medlyn, B. E. (2018). Triggers of tree mortality under drought. Nature 558, 531–539. doi: 10.1038/s41586-018-0240-x
Cochard, H. (2002). A technique for measuring xylem hydraulic conductance under high negative pressures. Plant Cell Environ. 25, 815–819. doi: 10.1046/j.1365-3040.2002.00863.x
Cochard, H. (2020). A new mechanism for tree mortality due to drought and heatwaves. Peer Commun. Forest Wood Sci. 17. doi: 10.1101/531632
Cochard, H., Pimont, F., Ruffault, J., and Martin-St. Paul, N. (2021). SurEau: a mechanistic model of plant water relations under extreme drought. Ann. For. Sci. 78, 1–23. doi: 10.1007/s13595-021-01067-y
Collatz, G. J., Ball, J. T., Grivet, C., and Berry, J. A. (1991). Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer. Agric. For. Meteorol. 54, 107–136. doi: 10.1016/0168-1923(91)90002-8
Damour, G., Simonneau, T., Cochard, H., and Urban, L. (2010). An overview of models of stomatal conductance at the leaf level. Plant Cell Environ. 33, 1419–1438. doi: 10.1111/j.1365-3040.2010.02181.x
De Kauwe, M. G., Medlyn, B. E., Ukkola, A. M., Mu, M., Sabot, M. E., Pitman, A. J., et al. (2020). Identifying areas at risk of drought-induced tree mortality across South-Eastern Australia. Glob. Chang. Biol. 26, 5716–5733. doi: 10.1111/gcb.15215
De Pury, D. G. G., and Farquhar, G. D. (1997). Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 20, 537–557. doi: 10.1111/j.1365-3040.1997.00094.x
Dietze, M. C., Fox, A., Beck-Johnson, L. M., Betancourt, J. L., Hooten, M. B., Jarnevich, C. S., et al. (2018). Iterative near-term ecological forecasting: needs, opportunities, and challenges. Proc. Nat. Acad. Sci. 115, 1424–1432. doi: 10.1073/pnas.1710231115
Drake, J. E., Power, S. A., Duursma, R. A., Medlyn, B. E., Aspinwall, M. J., Choat, B., et al. (2017). Stomatal and non-stomatal limitations of photosynthesis for four tree species under drought: a comparison of model formulations. Agric. For. Meteorol. 247, 454–466. doi: 10.1016/j.agrformet.2017.08.026
Duursma, R. A., Blackman, C. J., Lopéz, R., Martin-StPaul, N. K., Cochard, H., and Medlyn, B. E. (2019). On the minimum leaf conductance: its role in models of plant water use, and ecological and environmental controls. New Phytol. 221, 693–705. doi: 10.1111/nph.15395
Duursma, R. A., and Medlyn, B. E. (2012). MAESPA: a model to study interactions between water limitation, environmental drivers and vegetation function at tree and stand levels, with an example application to [CO 2] × drought interactions. Geosci. Model Dev. 5, 919–940. doi: 10.5194/gmd-5-919-2012
Eilmann, B., Dobbertin, M., and Rigling, A. (2013). Growth response of Scots pine with different crown transparency status to drought release. Ann. For. Sci. 70, 685–693. doi: 10.1007/s13595-013-0310-z
Eller, C. B., Rowland, L., Mencuccini, M., Rosas, T., Williams, K., Harper, A., et al. (2020). Stomatal optimization based on xylem hydraulics (SOX) improves land surface model simulation of vegetation responses to climate. New Phytol. 226, 1622–1637. doi: 10.1111/nph.16419
Eller, C. B., Rowland, L., Oliveira, R. S., Bittencourt, P. R., Barros, F. V., da Costa, A. C., et al. (2018). Modelling tropical forest responses to drought and El Niño with a stomatal optimization model based on xylem hydraulics. Philos. Transac. R. Soc. B Biol. Sci. 373:20170315. doi: 10.1098/rstb.2017.0315
Ellison, A. M. (2004). Bayesian inference in ecology. Ecol. Lett. 7, 509–520. doi: 10.1111/j.1461-0248.2004.00603.x
Escudero, A., and Mediavilla, S. (2003). Decline in photosynthetic nitrogen use efficiency with leaf age and nitrogen resorption as determinants of leaf life span. J. Ecol. 91, 880–889. doi: 10.1046/j.1365-2745.2003.00818.x
Evans, J. R. (2021). Mesophyll conductance: walls, membranes and spatial complexity. New Phytol. 229, 1864–1876. doi: 10.1111/nph.16968
Farquhar, G. D., von Caemmerer, S. V., and Berry, J. A. (1980). A biochemical model of photosynthetic CO2 assimilation in leaves of C 3 species. Planta 149, 78–90. doi: 10.1007/BF00386231
Fatichi, S., Leuzinger, S., and Körner, C. (2014). Moving beyond photosynthesis: from carbon source to sink-driven vegetation modeling. New Phytol. 201, 1086–1095. doi: 10.1111/nph.12614
Flexas, J., Barbour, M. M., Brendel, O., Cabrera, H. M., Carriquí, M., Diaz-Espejo, A., et al. (2012). Mesophyll diffusion conductance to CO2: an unappreciated central player in photosynthesis. Plant Sci. 193, 70–84. doi: 10.1016/j.plantsci.2012.05.009
Flexas, J., Bota, J., Cifre, J., Mariano Escalona, J., Galmés, J., Gulías, J., et al. (2004). Understanding down-regulation of photosynthesis under water stress: future prospects and searching for physiological tools for irrigation management. Ann. Appl. Biol. 144, 273–283. doi: 10.1111/j.1744-7348.2004.tb00343.x
Flexas, J., Diaz-Espejo, A., Galmes, J., Kaldenhoff, R., Medrano, H., Ribas-Carbo, M., et al. (2007). Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant Cell Environ. 30, 1284–1298. doi: 10.1111/j.1365-3040.2007.01700.x
Galiano, L., Martínez-Vilalta, J., and Lloret, F. (2011). Carbon reserves and canopy defoliation determine the recovery of Scots pine 4 yr after a drought episode. New Phytol. 190, 750–759. doi: 10.1111/j.1469-8137.2010.03628.x
Gelman, A., and Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472. doi: 10.1214/ss/1177011136
Gourlez de la Motte, L., Beauclaire, Q., Heinesch, B., Cuntz, M., Foltýnová, L., Šigut, L., et al. (2020). Non-stomatal processes reduce gross primary productivity in temperate forest ecosystems during severe edaphic drought. Philos. Transac. R. Soc. B 375:20190527. doi: 10.1098/rstb.2019.0527
Hall, A. E., and Kaufmann, M. R. (1975). Stomatal response to environment with Sesamum indicum. L. Plant Physiol. 55, 455–459. doi: 10.1104/pp.55.3.455
Hammond, W. M., Yu, K., Wilson, L. A., Will, R. E., Anderegg, W. R., and Adams, H. D. (2019). Dead or dying? Quantifying the point of no return from hydraulic failure in drought-induced tree mortality. New Phytol. 223, 1834–1843. doi: 10.1111/nph.15922
Hari, V., Rakovec, O., Markonis, Y., Hanel, M., and Kumar, R. (2020). Increased future occurrences of the exceptional 2018–2019 Central European drought under global warming. Sci. Rep. 10, 1–10. doi: 10.1038/s41598-020-68872-9
Harley, P. C., Thomas, R. B., Reynolds, J. F., and Strain, B. R. (1992). Modelling photosynthesis of cotton grown in elevated CO2. Plant Cell Environ. 15, 271–282. doi: 10.1111/j.1365-3040.1992.tb00974.x
Hartig, F., Dyke, J., Hickler, T., Higgins, S. I., O'Hara, R. B., Scheiter, S., et al. (2012). Connecting dynamic vegetation models to data–an inverse perspective. J. Biogeogr. 39, 2240–2252. doi: 10.1111/j.1365-2699.2012.02745.x
Hartig, F., Minunno, F., and Paul, S. (2017). BayesianTools: general-purpose MCMC and SMC samplers and tools for Bayesian statistics, R package version 0.1.3. Available online at: https://cran.r-project.org/web/packages/BayesianTools/vignettes/BayesianTools.html
Hesse, B. D., Goisser, M., Hartmann, H., and Grams, T. E. (2019). Repeated summer drought delays sugar export from the leaf and impairs phloem transport in mature beech. Tree Physiol. 39, 192–200. doi: 10.1093/treephys/tpy122
Hochberg, U., Windt, C. W., Ponomarenko, A., Zhang, Y. J., Gersony, J., Rockwell, F. E., et al. (2017). Stomatal closure, basal leaf embolism, and shedding protect the hydraulic integrity of grape stems. Plant Physiol. 174, 764–775. doi: 10.1104/pp.16.01816
Hsiao, T. C., Acevedo, E., Fereres, E., and Henderson, D. W. (1976). Water stress, growth and osmotic adjustment. Philos. Transac. R. Soc. Lond. B Biol. Sci. 273, 479–500. doi: 10.1098/rstb.1976.0026
Ichie, T., Hiromi, T., Yoneda, R., Kamiya, K., Kohira, M., Ninomiya, I., et al. (2004). Short-term drought causes synchronous leaf shedding and flushing in a lowland mixed dipterocarp forest, Sarawak, Malaysia. J. Trop. Ecol. 697–700. doi: 10.1017/S0266467404001713
Kannenberg, S. A., Schwalm, C. R., and Anderegg, W. R. (2020). Ghosts of the past: how drought legacy effects shape forest functioning and carbon cycling. Ecol. Lett. 23, 891–901. doi: 10.1111/ele.13485
Keenan, T., Sabate, S., and Gracia, C. (2010). Soil water stress and coupled photosynthesis–conductance models: bridging the gap between conflicting reports on the relative roles of stomatal, mesophyll conductance and biochemical limitations to photosynthesis. Agric. For. Meteorol. 150, 443–453. doi: 10.1016/j.agrformet.2010.01.008
Leuning, R. (1995). A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ. 18, 339–355. doi: 10.1111/j.1365-3040.1995.tb00370.x
Li, X., Smith, R., Choat, B., and Tissue, D. T. (2020). Drought resistance of cotton (Gossypium hirsutum) is promoted by early stomatal closure and leaf shedding. Funct. Plant Biol. 47, 91–98. doi: 10.1071/FP19093
Marchin, R., Zeng, H., and Hoffmann, W. (2010). Drought-deciduous behavior reduces nutrient losses from temperate deciduous trees under severe drought. Oecologia 163, 845–854. doi: 10.1007/s00442-010-1614-4
Martínez-Vilalta, J., Poyatos, R., Aguadé, D., Retana, J., and Mencuccini, M. (2014). A new look at water transport regulation in plants. New Phytol. 204, 105–115. doi: 10.1111/nph.12912
Martin-St. Paul, N., Delzon, S., and Cochard, H. (2017). Plant resistance to drought depends on timely stomatal closure. Ecol. Lett. 20, 1437–1447. doi: 10.1111/ele.12851
Martin-St. Paul, N. K., Limousin, J. M., Vogt-Schilb, H., Rodríguez-Calcerrada, J., Rambal, S., Longepierre, D., et al. (2013). The temporal response to drought in a Mediterranean evergreen tree: comparing a regional precipitation gradient and a throughfall exclusion experiment. Glob. Chang. Biol. 19, 2413–2426. doi: 10.1111/gcb.12215
Martorell, S., Diaz-Espejo, A., Medrano, H., Ball, M. C., and Choat, B. (2014). Rapid hydraulic recovery in Eucalyptus pauciflora after drought: linkages between stem hydraulics and leaf gas exchange. Plant Cell Environ. 37, 617–626. doi: 10.1111/pce.12182
McDowell, N., Allen, C. D., Anderson-Teixeira, K., Brando, P., Brienen, R., Chambers, J., et al. (2018). Drivers and mechanisms of tree mortality in moist tropical forests. New Phytol. 219, 851–869. doi: 10.1111/nph.15027
Medlyn, B. E., Duursma, R. A., Eamus, D., Ellsworth, D. S., Prentice, I. C., Barton, C. V., et al. (2011). Reconciling the optimal and empirical approaches to modelling stomatal conductance. Glob. Chang. Biol. 17, 2134–2144. doi: 10.1111/j.1365-2486.2010.02375.x
Medlyn, B. E., Zaehle, S., De Kauwe, M. G., Walker, A. P., Dietze, M. C., Hanson, P. J., et al. (2015). Using ecosystem experiments to improve vegetation models. Nat. Clim. Chang. 5, 528–534. doi: 10.1038/nclimate2621
Meir, P., Mencuccini, M., and Dewar, R. C. (2015). Drought-related tree mortality: addressing the gaps in understanding and prediction. New Phytol. 207, 28–33. doi: 10.1111/nph.13382
Mencuccini, M., Manzoni, S., and Christoffersen, B. (2019). Modelling water fluxes in plants: from tissues to biosphere. New Phytol. 222, 1207–1222. doi: 10.1111/nph.15681
Monteith, J. L. (1995). A reinterpretation of stomatal responses to humidity. Plant Cell Environ. 18, 357–364. doi: 10.1111/j.1365-3040.1995.tb00371.x
Montserrat-Marti, G., Camarero, J. J., Palacio, S., Pérez-Rontomé, C., Milla, R., Albuixech, J., et al. (2009). Summer-drought constrains the phenology and growth of two coexisting Mediterranean oaks with contrasting leaf habit: implications for their persistence and reproduction. Trees 23, 787–799. doi: 10.1007/s00468-009-0320-5
Mu, M., De Kauwe, M. G., Ukkola, A. M., Pitman, A. J., Gimeno, T. E., Medlyn, B. E., et al. (2021). Evaluating a land surface model at a water-limited site: implications for land surface contributions to droughts and heatwaves. Hydrol. Earth Syst. Sci. 25, 447–471. doi: 10.5194/hess-25-447-2021
Mullen, K., Ardia, D., Gil, D. L., Windover, D., and Cline, J. (2011). DEoptim: an R package for global optimization by differential evolution. J. Stat. Softw. 40, 1–26. doi: 10.18637/jss.v040.i06
Munné-Bosch, S., and Alegre, L. (2004). Die and let live: leaf senescence contributes to plant survival under drought stress. Funct. Plant Biol. 31, 203–216. doi: 10.1071/FP03236
Nadal-Sala, D., Grote, R., Birami, B., Lintunen, A., Mammarella, I., Preisler, Y., and Ruehr, N. K. (2021). Assessing model performance via the most limiting environmental driver in two differently stressed pine stands. Ecol. Appl. 31:e02312. doi: 10.1002/eap.2312
Niinemets, Ü., Cescatti, A., Rodeghiero, M., and Tosens, T. (2006). Complex adjustments of photosynthetic potentials and internal diffusion conductance to current and previous light availabilities and leaf age in Mediterranean evergreen species Quercus ilex. Plant Cell Environ. 29, 1159–1178. doi: 10.1111/j.1365-3040.2006.01499.x
Niinemets, Ü., and Sack, L. (2006). “Structural determinants of leaf light-harvesting capacity and photosynthetic potentials,” in Progress in Botany (Berlin; Heidelberg: Springer), 385–419.
Niinemets, Ü. L. O., Cescatti, A., Rodeghiero, M., and Tosens, T. (2005). Leaf internal diffusion conductance limits photosynthesis more strongly in older leaves of Mediterranean evergreen broad-leaved species. Plant Cell Environ. 28, 1552–1566. doi: 10.1111/j.1365-3040.2005.01392.x
Ogaya, R., and Penuelas, J. (2004). Phenological patterns of Quercus ilex, Phillyrea latifolia, and Arbutus unedo growing under a field experimental drought. Ecoscience 11, 263–270. doi: 10.1080/11956860.2004.11682831
Paudel, I., Gerbi, H., Zisovich, A., Sapir, G., Ben-Dor, S., Brumfeld, V., et al. (2019). Drought tolerance mechanisms and aquaporin expression of wild vs. cultivated pear tree species in the field. Environ. Exp. Bot. 167:103832. doi: 10.1016/j.envexpbot.2019.103832
Pilon, C., Snider, J. L., Sobolev, V., Chastain, D. R., Sorensen, R. B., Meeks, C. D., et al. (2018). Assessing stomatal and non-stomatal limitations to carbon assimilation under progressive drought in peanut (Arachishypogaea L.). J. Plant Physiol. 231, 124–134. doi: 10.1016/j.jplph.2018.09.007
Pineda-García, F., Paz, H., and Meinzer, F. C. (2013). Drought resistance in early and late secondary successional species from a tropical dry forest: the interplay between xylem resistance to embolism, sapwood water storage and leaf shedding. Plant Cell Environ. 36, 405–418. doi: 10.1111/j.1365-3040.2012.02582.x
Pinheiro, J., Bates, D., DebRoy, S., and Sarkar, D. (2021). nlme: Linear and Nonlinear Mixed Effects Models. R package version 3. 1–152.
Poyatos, R., Aguadé, D., Galiano, L., Mencuccini, M., and Martínez-Vilalta, J. (2013). Drought-induced defoliation and long periods of near-zero gas exchange play a key role in accentuating metabolic decline of Scots pine. New Phytol. 200, 388–401. doi: 10.1111/nph,0.12278
R Core Team (2021). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: https://www.R-project.org/
Reich, P. B., Sendall, K. M., Stefanski, A., Rich, R. L., Hobbie, S. E., and Montgomery, R. A. (2018). Effects of climate warming on photosynthesis in boreal tree species depend on soil moisture. Nature 562, 263–267. doi: 10.1038/s41586-018-0582-4
Riesmeier, J. W., Willmitzer, L., and Frommer, W. B. (1994). Evidence for an essential role of the sucrose transporter in phloem loading and assimilate partitioning. EMBO J. 13, 1–7. doi: 10.1002/j.1460-2075.1994.tb06229.x
Rizhsky, L., Liang, H., and Mittler, R. (2002). The combined effect of drought stress and heat shock on gene expression in tobacco. Plant Physiol. 130, 1143–1151. doi: 10.1104/pp.006858
Ruehr, N. K., Gast, A., Weber, C., Daub, B., and Arneth, A. (2016). Water availability as dominant control of heat stress responses in two contrasting tree species. Tree Physiol. 36, 164–178. doi: 10.1093/treephys/tpv102
Ruehr, N. K., Grote, R., Mayr, S., and Arneth, A. (2019). Beyond the extreme: recovery of carbon and water relations in woody plants following heat and drought stress. Tree Physiol. 39, 1285–1299. doi: 10.1093/treephys/tpz032
Sala, A., Piper, F., and Hoch, G. (2010). Physiological mechanisms of drought-induced tree mortality are far from being resolved. New Phytol. 186, 274–281. doi: 10.1111/j.1469-8137.2009.03167.x
Schuldt, B., Buras, A., Arend, M., Vitasse, Y., Beierkuhnlein, C., Damm, A., et al. (2020). A first assessment of the impact of the extreme 2018 summer drought on Central European forests. Basic Appl. Ecol. 45, 86–103. doi: 10.1016/j.baae.2020.04.003
Schumann, K., Leuschner, C., and Schuldt, B. (2019). Xylem hydraulic safety and efficiency in relation to leaf and wood traits in three temperate Acer species differing in habitat preferences. Trees Struct. Funct. 33. 1475–1490. doi: 10.1007/s00468-019-01874-x
Schuster, A. C., Burghardt, M., Alfarhan, A., Bueno, A., Hedrich, R., Leide, J., et al. (2016). Effectiveness of cuticular transpiration barriers in a desert plant at controlling water loss at high temperatures. AoB Plants 8:plw027. doi: 10.1093/aobpla/plw027
Sevanto, S. (2014). Phloem transport and drought. J. Exp. Bot. 65, 1751–1759. doi: 10.1093/jxb/ert467
Sperry, J. S., and Love, D. M. (2015). What plant hydraulics can tell us about responses to climate-change droughts. New Phytol. 207, 14–27. doi: 10.1111/nph.13354
Sperry, J. S., Venturas, M. D., Anderegg, W. R., Mencuccini, M., Mackay, D. S., Wang, Y., et al. (2017). Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost. Plant Cell Environ. 40, 816–830. doi: 10.1111/pce.12852
Sperry, J. S., Venturas, M. D., Todd, H. N., Trugman, A. T., Anderegg, W. R., Wang, Y., et al. (2019). The impact of rising CO2 and acclimation on the response of US forests to global warming. Proc. Nat. Acad. Sci. 116, 25734–25744. doi: 10.1073/pnas.1913072116
Sugiura, D., Terashima, I., and Evans, J. R. (2020). A decrease in mesophyll conductance by cell-wall thickening contributes to photosynthetic downregulation. Plant Physiol. 183, 1600–1611. doi: 10.1104/pp.20.00328
terBraak, C. J., and Vrugt, J. A. (2008). Differential evolution Markov chain with snooker updater and fewer chains. Stat. Comput. 18, 435–446. doi: 10.1007/s11222-008-9104-9
Tuzet, A., Perrier, A., and Leuning, R. (2003). A coupled model of stomatal conductance, photosynthesis and transpiration. Plant Cell Environ. 26, 1097–1116. doi: 10.1046/j.1365-3040.2003.01035.x
Tyree, M. T., and Ewers, F. W. (1991). The hydraulic architecture of trees and other woody plants. New Phytol. 119, 345–360. doi: 10.1111/j.1469-8137.1991.tb00035.x
Velikova, V., Arena, C., Izzo, L. G., Tsonev, T., Koleva, D., Tattini, M., et al. (2020). Functional and structural leaf plasticity determine photosynthetic performances during drought stress and recovery in two Platanusorientalispopulations from contrasting habitats. Int. J. Mol. Sci. 21:3912. doi: 10.3390/ijms21113912
Vilagrosa, A., Bellot, J., Vallejo, V. R., and Gil-Pelegrín, E. (2003). Cavitation, stomatal conductance, and leaf dieback in seedlings of two co-occurring Mediterranean shrubs during an intense drought. J. Exp. Bot. 54, 2015–2024. doi: 10.1093/jxb/erg221
Wang, K. Y., Kellomäki, S., and Laitinen, K. (1996). Acclimation of photosynthetic parameters in Scots pine after three years exposure to elevated temperature and CO2. Agric. For. Meteorol. 82, 195–217. doi: 10.1016/0168-1923(96)02329-5
Whitehead, D., Edwards, W. R. N., and Jarvis, P. G. (1984). Conducting sapwood area, foliage area, and permeability in mature trees of Piceasitchensis and Pinus contorta. Can. J. For. Res. 14, 940–947. doi: 10.1139/x84-166
Wolfe, B. T., Sperry, J. S., and Kursar, T. A. (2016). Does leaf shedding protect stems from cavitation during seasonal droughts? A test of the hydraulic fuse hypothesis. New Phytol. 212, 1007–1018 doi: 10.1111/nph.14087
Xu, L., and Baldocchi, D. D. (2003). Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree Physiol. 23, 865–877. doi: 10.1093/treephys/23.13.865
Yan, W., Zhong, Y., and Shangguan, Z. (2017). Rapid response of the carbon balance strategy in Robinia pseudoacacia and Amorphafruticosa to recurrent drought. Environ. Exp. Bot. 138, 46–56. doi: 10.1016/j.envexpbot.2017.03.009
Yang, J., Duursma, R. A., De Kauwe, M. G., Kumarathunge, D., Jiang, M., Mahmud, K., et al. (2019). Incorporating non-stomatal limitation improves the performance of leaf and canopy models at high vapour pressure deficit. Tree Physiol. 39, 1961–1974. doi: 10.1093/treephys/tpz103
Keywords: leaf shedding, non-stomatal limitations of photosynthesis, Scots pine, tree hydraulic simulation models, xylem vulnerability
Citation: Nadal-Sala D, Grote R, Birami B, Knüver T, Rehschuh R, Schwarz S and Ruehr NK (2021) Leaf Shedding and Non-Stomatal Limitations of Photosynthesis Mitigate Hydraulic Conductance Losses in Scots Pine Saplings During Severe Drought Stress. Front. Plant Sci. 12:715127. doi: 10.3389/fpls.2021.715127
Received: 26 May 2021; Accepted: 08 July 2021;
Published: 03 September 2021.
Edited by:
Amanda A. Cardoso, Federal University of Alfenas, BrazilReviewed by:
Samuel Cordeiro Vitor Martins, Universidade Federal de Viçosa, BrazilVirginia Hernandez-Santana, Institute of Natural Resources and Agrobiology of Seville (CSIC), Spain
Alexandria Pivovaroff, Pacific Northwest National Laboratory (DOE), United States
Copyright © 2021 Nadal-Sala, Grote, Birami, Knüver, Rehschuh, Schwarz and Ruehr. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Nadal-Sala, ZC5uYWRhbEBraXQuZWR1
 Daniel Nadal-Sala
Daniel Nadal-Sala Rüdiger Grote
Rüdiger Grote Benjamin Birami
Benjamin Birami Timo Knüver1,3
Timo Knüver1,3 Romy Rehschuh
Romy Rehschuh Nadine K. Ruehr
Nadine K. Ruehr