- 1Plant Biomechanics Group @ Botanic Garden, University of Freiburg, Freiburg, Germany
- 2Cluster of Excellence livMatS @ FIT – Freiburg Center for Interactive Materials and Bioinspired Technologies, University of Freiburg, Freiburg, Germany
- 3Department of Microsystems Engineering – IMTEK, University of Freiburg, Freiburg, Germany
From a mechanical viewpoint, petioles of foliage leaves are subject to contradictory mechanical requirements. High flexural rigidity guarantees support of the lamina and low torsional rigidity ensures streamlining of the leaves in wind. This mechanical trade-off between flexural and torsional rigidity is described by the twist-to-bend ratio. The safety factor describes the maximum load capacity. We selected four herbaceous species with different body plans (monocotyledonous, dicotyledonous) and spatial configurations of petiole and lamina (2-dimensional, 3-dimensional) and carried out morphological-anatomical studies, two-point bending tests and torsional tests on the petioles to analyze the influence of geometry, size and shape on their twist-to-bend ratio and safety factor. The monocotyledons studied had significantly higher twist-to-bend ratios (23.7 and 39.2) than the dicotyledons (11.5 and 13.3). High twist-to-bend ratios can be geometry-based, which is true for the U-profile of Hosta x tardiana with a ratio of axial second moment of area to torsion constant of over 1.0. High twist-to-bend ratios can also be material-based, as found for the petioles of Caladium bicolor with a ratio of bending elastic modulus and torsional modulus of 64. The safety factors range between 1.7 and 2.9, meaning that each petiole can support about double to triple the leaf’s weight.
Introduction
The petioles of foliage leaves fulfill various functions with sometimes contradictory demands. Their functions include aligning the lamina to the sun for photosynthesis (Niinemets and Fleck, 2002), vascularly connecting the lamina to the stem, supporting the weight of the lamina and elastically yielding under wind load to prevent the leaf from tearing. Of particular importance is the mechanical compromise of high flexural rigidity, which allows the petiole to be stiff enough under the bending load of the self-weight of the leaf (Vogel, 1992; Niklas, 1999), and a comparatively low torsional rigidity, which enables the petiole to be flexible enough to avoid damaging influences by wind loads (Vogel, 1989; Niklas, 1996). This biomechanical trade-off is reflected in the dimensionless twist-to-bend ratio (EI/GJ) (Vogel, 1992), which describes the flexural (bending) rigidity (EI) compared with the torsional rigidity (GJ) (Wainwright et al., 1976; Vogel, 1992; Etnier, 2003).
Another important mechanical aspect of biological structures is the dimensionless safety factor (SF), which estimates the maximum carrying capacity of the structures. In other words: the safety factor describes the extent to which the structure can carry more than its own static load (Gere, 2004). Both the twist-to-bend ratio EI/GJ and the safety factor SF are dimensionless variables and therefore allow comparisons to be made between various structures (Vogel, 1992, 1995, 2007; Niklas, 1999; Etnier, 2003). This is crucial as leaves and their petioles show a wide variety of morphological and anatomical characteristics. One aspect is the spatial configuration of the lamina and petiole, described by Langer et al. (2021) as three-dimensional (3D) for peltate leaves and two-dimensional (2D) for leaves in which the petiole is attached to the lamina base. Moreover, marked differences are found between the cross-sectional geometries of petioles, which can be circular, elliptical or U-profiled (Vogel, 1992; Ennos et al., 2000; Pasini and Mirjalili, 2006). Finally, differences occur in the body plan of herbaceous plants.
The term “body plan” was coined by Drost et al. (2017) and describes morphological features shared between species within a phylum. In this study, it is used to describe the internal arrangement of the vascular tissues in relation to mono- and dicotyledonous species.
The aspects mentioned above in turn influence the mechanics of the petioles. The configuration affects the way in which the applied loads act on the petioles, whereas the geometry, size and shape of the petioles affect their geometric characteristics, such as the axial (I) and polar (J) second moments of area and the torsion constant (K). The torsion constant (K) comes into play because, unlike the polar second moment of area (J), it takes into account the warping of non-circular structures under torsional loading and thus is often much smaller than J (Young et al., 2002). The body plan includes the arrangement of the vascular bundles that represent a type of strengthening tissue, which influences the material properties of the leaf, such as the bending elastic modulus (E) and torsional modulus (G).
We aimed to answer to the following scientific question: “How do cross-sectional geometry, sizes and shapes of petioles influence their twist-to-bend ratio and safety factor?”. Therefore, we selected four distinct types of petioles having a mono- or dicotyledonous body plan and/or a 3-dimenisonal (=peltate) or 2-dimensional (=petiole attached at the basis of the lamina) configuration of petiole and lamina. We obtained the necessary data through morphological and anatomical investigations and by two-point bending tests and torsional tests. In addition to the previously existing formula for the safety factor of vertically oriented structures, we provide, for the first time, an equation to calculate the safety factor of naturally horizontally oriented petioles. For the calculation of the twist-to-bend ratio, we did not use the polar second moment of area, as is usually the case, but the torsion constant, as the latter takes into account the warping of the structure during torsion.
Materials and Methods
Plant Material
Plants of the species Hosta x tardiana ‘El Niño’ Piet Warmerdam (patent PP14632) (hereafter H. tardiana), Caladium bicolor Vent. (hereafter C. bicolor), Hemigraphis alternata (L.) Hallier f. (hereafter H. alternata), and Pilea peperomioides Diels (hereafter P. peperomioides) were cultivated in the greenhouse of the Botanic Garden (University of Freiburg, Germany). These four species were selected based on the same criteria as those described by Langer et al. (2021): (1) two species of each body plan (monocotyledonous and dicotyledonous) having a foliage leaf with either a 2D or 3D spatial configuration of petiole and lamina, (3) herbaceous, (4) perennial, and (5) easy to cultivate to provide sufficient material for experimentation. One random leaf of each of the 25 plants studied per species was investigated (Figure 1).

Figure 1. Leaf morphology of (A) Hosta × tardiana ‘El Niño’, (B) Caladium bicolor, (C) Hemigraphis alternata, and (D) Pilea peperomioides. Scale bar is 20 mm.
Morphology
We weighed the lamina and petioles on a digital balance (accuracy ± 0.001 g). The weight ratio WR of the lamina wlamina to the petiole wpetiole was calculated according to:
The diameters in the lateral direction dlateral and in the adaxial-abaxial direction dadaxial of each leaf stalk (petiole) were measured every 0.5 cm for H. alternata, every 1 cm for H. tardiana and P. peperomioides and every 3 cm for C. bicolor by a digital caliper (accuracy ± 0.01 mm). The aspect ratio AR of these perpendicular diameters gives an indication of the cross-sectional shape of the petioles, i.e., an AR of 1 means that the cross-section is as wide as it is high. This ratio was calculated as follows:
The tapering mode α is a dimensionless parameter that describes the shape of a slender structure (Figure 2), which is, in our case, the petiole. Calculations of the tapering mode were based on the formulae published by Caliaro et al. (2013). First, we calculated the equivalent radius to account for non-perfectly circular cross-sections:
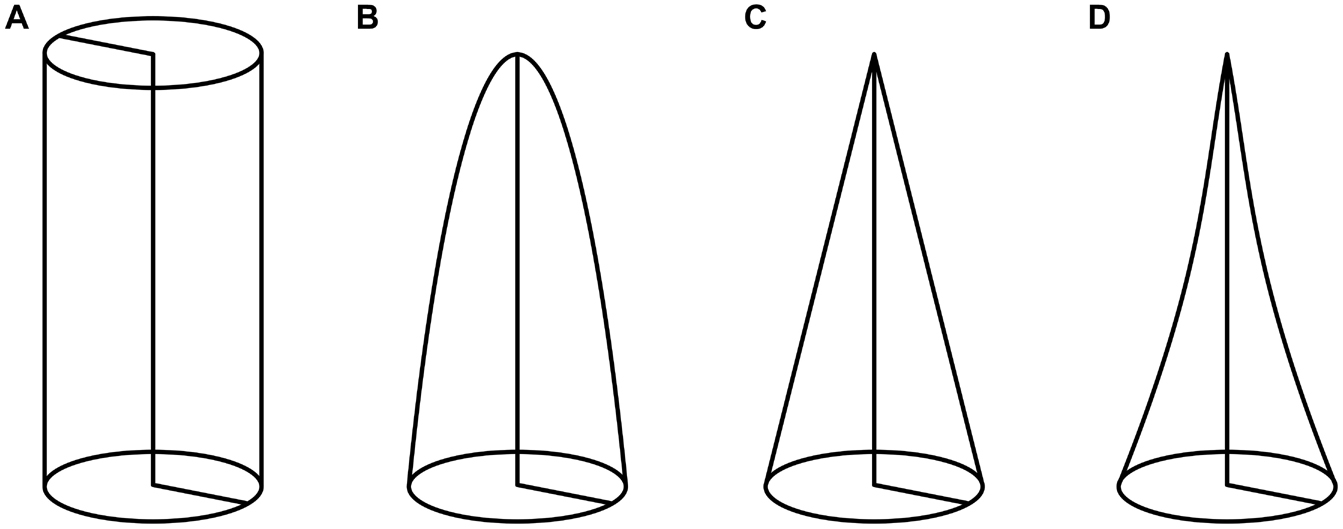
Figure 2. Tapering modes α of various slender structures: (A) α = 0 represents a circular cylinder, (B) α = 0.5 a second order paraboloid of revolution, (C) α = 1 a circular cone, and (D) α = 1.5 a hyperboloid of revolution.
where radaxial is the radius in the adaxial-abaxial direction (which is also the bending direction in which the force acts) and rlateral is the radius in the lateral direction (perpendicular to the bending direction). The radii radaxial and rlateral were derived from the corresponding measured diameters. Thereafter, the tapering mode α was derived based on the equation:
with r(x) being the equivalent radius at the distance x from the basal end of the petiole, rapical being the equivalent radius of the apical end (x = L), rbasal being the equivalent radius of the basal end (x = 0) and L being the length of the petiole. The numerator was plotted against the denominator and the slope of the linear regression represented the tapering mode α.
Anatomy and Histology
After mechanical testing, we divided the petioles into thirds, with 1 cm of the basal, middle and apical part of each petiole being frozen onto a metal sample holder by means of a freezing solution (Tissue-Tek O.C.T. Compound, Sakura Finetek Japan Co., Tokyo, Japan). Transverse thin sections with a thickness of 100 μm were cut on a rotatory cryotome (MEV, SLEE medical, Mainz, Germany). After bleaching the sections (20% eau de Javel), we immersed them in a 0.05% w/v solution of toluidine blue O, which stained non-lignified tissue red-purple and lignified tissue blue to dark violet (Sakai, 1973). The stained sections were imaged via an Olympus BX61 microscope (Olympus, Tokyo, Japan) equipped with a CP71 camera module. We determined the axial second moment of area I and polar second moment of area J for each section by using the BoneJ2 Plugin (Version 6.1.0) (Doube et al., 2010) provided in Fiji software (ImageJ Version 1.52p) (Schindelin et al., 2012). These geometric variables describe the influence of the cross-sectional shape of a specimen on its mechanical behavior, for example under bending (I) or torsional loads (J). The higher these geometrical characteristics are, the more the geometries resist mechanical loads/deformations.
Another variable useful for analyzing the influence of the cross-sectional geometry on the torsional behavior is the torsion constant K. K is part of the following equation expressing torsional rigidity:
where θ is the angle of twist in radians, T the twisting moment, L the length of the bar and G the torsional modulus. K is equal to the polar second moment of area J, provided that the cross-section is perfectly circular. For other cross-sectional geometries, however, K is smaller than J and, in some cases, is only a small fraction of it (Young et al., 2002). Therefore, different equations are needed for the various cross-sectional geometries. All equations have been taken from Table 10.1 of Young et al. (2002). The petioles of C. bicolor and P. peperomioides are almost circular and have therefore been assumed to be circles; the following equation can thus be used to calculate K, which, in this case, equals J:
with r being the radius of the circle. The petioles of H. alternata are elliptical and, therefore, K has been calculated according to the following equation:
where radaxial is the radius in adaxial-abaxial direction and rlateral the radius in lateral direction of the ellipse. For the U-profile of the petioles of H. tardiana, K has been calculated as follows:
with U being the length of the median line through the U-profile and t the thickness of the U-profile. However, this formula is limited to a uniform thickness of the U-profile, which is not the case with the cross-sectional geometry of the petioles of Hosta x tardiana ‘El Niño’. Therefore, we measured the thickness for each cross-section, always at the same five points of the cross-section, and calculated the mean thickness (Figure 3). This mean value was then used as t in the formula. The median line U was placed through the vascular bundles in each cross-section (Figure 3).
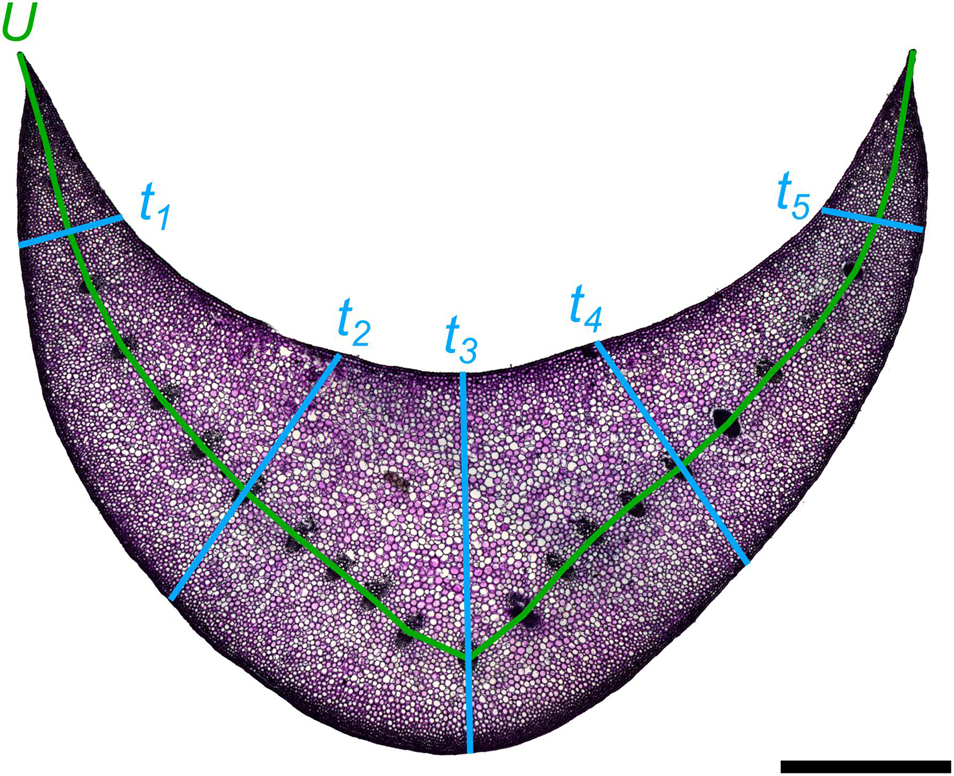
Figure 3. Exemplary cross-section of the petiole of Hosta x tardiana ‘El Niño’ with five measuring points for the thicknesses (t1–t5) and the median line U. The scale bar is 2 mm.
Biomechanics
Petiole samples were glued basally into 3D-printed PLA (polylactide) clamps by using ethyl cyanoacrylate as the adhesive (LOCTITE® 401, Henkel AG & Co., KGaA, Düsseldorf, Germany). The clamps were fixed within a custom-built uniaxial measurement device and two-point bending tests were performed. The petioles were always bent in the abaxial direction. The device was equipped with a 1 N force sensor (Burster 8510– 5001, Burster Präzisionstechnik GmbH & Co., KG, Gernsbach, Germany) with a data acquisition rate of one value per 0.09 mm deflection. Then the apical ends were glued into the PLA clamps and the samples were fixed into the custom-build manual torsional test device (Gallenmüller et al., 2001). Torque was manually applied by a spring-loaded cylinder (spring constant c = 0.006 Nm–1) and the resulting angles were recorded. In order to evaluate the structural resistance of the specimens to the mechanical stresses/deformations (bending and torsion), the flexural rigidity EI and torsional rigidity GK were calculated according to:
where Lreal is the sample length, bbending the slope in the displacement-force diagram and btorsion the slope in the angular deflection-torque diagram. We calculated the torsional rigidity GK by using the torsion constant K, which is valid for cross-sections of any geometry, unlike the polar second moment of area J, which is valid only for circular cross-sections. Based on Equations (9) and (10) and the approach of Caliaro et al. (2013), we calculated the elastic modulus Eand torsional modulus G taking into consideration the tapering mode:
with Ibasal being the axial second moment of area at the basal end of the petiole, rbasal the equivalent radius of the petiole at the basal end, rapical the equivalent radius of the petiole at the apical end, α the tapering mode and Kbasal the torsion constant at the basal end of the petiole. E and G describe the resistance of the material on bending or torsional deformations.
The safety factor SF describes the multiple by which the structures can carry more than their actual static load. For the petioles, the SF was calculated as the ratio between the critical length (Lmax) and the real length (Lreal):
The challenge of the calculation of the critical length Lmax at which a slender and vertically oriented structure (pole) buckles was first solved analytically for selected pole forms and a continuous mass distribution along the poles without additional top load (Greenhill, 1881). Speck (1994) developed a formula based on the approach of Greenhill (1881) who took into consideration a top load in addition to a mass continuously distributed along the poles. The formula of Speck (1994) was used to calculate Lmax for the peltate leaves of C. bicolor and P. peperomioides, whose nearly vertically oriented petioles bear the lamina as a top load:
where c is a shape factor depending on the tapering mode and weight distribution along the petiole (c = 1.96 for C. bicolor and P. peperomioides), Flamina is the top load caused by the weight of the lamina, Fpetiole is the load induced by the self-weight of the petiole and γ is the specific weight of the petiole.
However, none of these approaches, which are all based on Euler’s critical buckling length calculations for slender upright poles, is suitable for calculating the critical buckling length Lmax of horizontally oriented plant structures, such as the petioles of H. tardiana and H. alternata. For this calculation, we considered horizontally oriented petioles as cantilever beams clamped on one side. We then considered the deflection δ of these beams under two different loading scenarios. To account for the deflection attributable to the self-weight of the petiole δpetiole, we used the following conventional formula for a (continuously) distributed load over the petiole:
In addition, we calculated the deflection caused by the weight of the lamina as a top load:
The total deflection δ was calculated by summing up the individual deflections:
The solution of Equation (17) according to the length of the petiole yielded:
Finally, we made the assumption that a deflection δ equal to the length of the petiole Lreal will inevitably lead to a buckling failure. Thus, if Lreal is substituted for δ in Equation (18), the critical length Lmax is obtained as follows:
However, in formula (19), the tapering mode α is not taken into account. Since we found tapered petioles in all the species studied, the tapering mode α was included in the flexural rigidity EI, similar to the approach given by Caliaro et al. (2013) for the elastic modulus E in Equation (11). The first term is the conventional equation for calculating the elastic modulus in two-point bending tests, with the assumption of a constant axial second moment of area I. The tapering mode α is included via the added second term, which incorporates a change in the axial second moment of area I based on its value at the base of the petiole (Ibasal). Rearrangement of this equation according to EI yields an EItapered depending on the tapering mode:
Finally, we substituted EItapered for EI in Equation (19) and obtained the critical length Lmax of a horizontally oriented petiole taking into account the tapering mode:
This formula was used to calculate Lmax for H. tardiana and H. alternata.
Statistical Analysis
All raw data are included in Supplementary Table 1. We used the software GNU R 4.0.0 for statistical analyses (R Core Team, 2021). The data were tested for normal distribution (Shapiro-Wilk test) and for homoscedasticity of variances (Levene test). Since all data are non-normally distributed, we present median values with corresponding interquartile ranges in brackets (IQR). We tested for significance at a significance level of 5% and performed Kruskal-Wallis tests together with Mann-Whitney-U post hoc tests (with p-value adjustments according to Holm, 1979) for unpaired data (p-values are given in Supplementary Table 2).
Results
To analyze the form-function relationship of the selected petioles, we focused on four key aspects: geometry, size, shape and biomechanics. In Table 1, we present our results as median values and corresponding IQR (in brackets). In addition, the results of the statistical analyses (p-values) are provided in Supplementary Table 2.
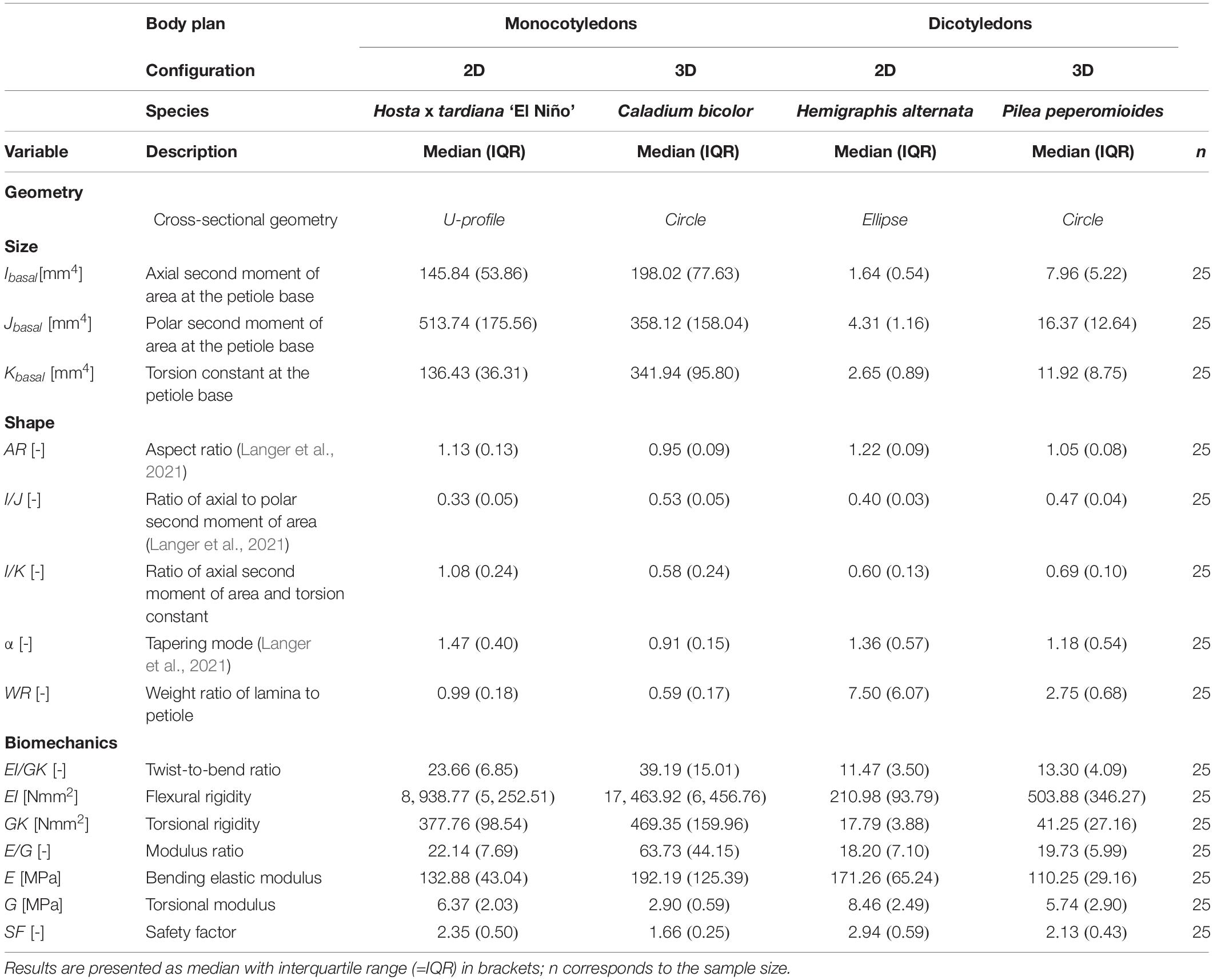
Table 1. Descriptive statistics of the variables of the petioles of Hosta × tardiana ‘El Niño’, Caladium bicolor, Hemigraphis alternata, and Pilea peperomioides giving an overall view of all numerical findings.
Geometry and Anatomy
The cross-sectional geometries of the petiole types varied from circular (C. bicolor, P. peperomioides) to elliptical (H. alternata) or were U-profiled (H. tardiana) (Figure 4). In addition to the epidermis, the parenchyma and the vascular tissue, we found strengthening tissues: C. bicolor (Figure 4B) has individual strands of collenchyma fibers in the periphery of the cross-section, whereas, in H. alternata (Figure 4C), the strengthening tissue forms a peripheral hypodermal ring.
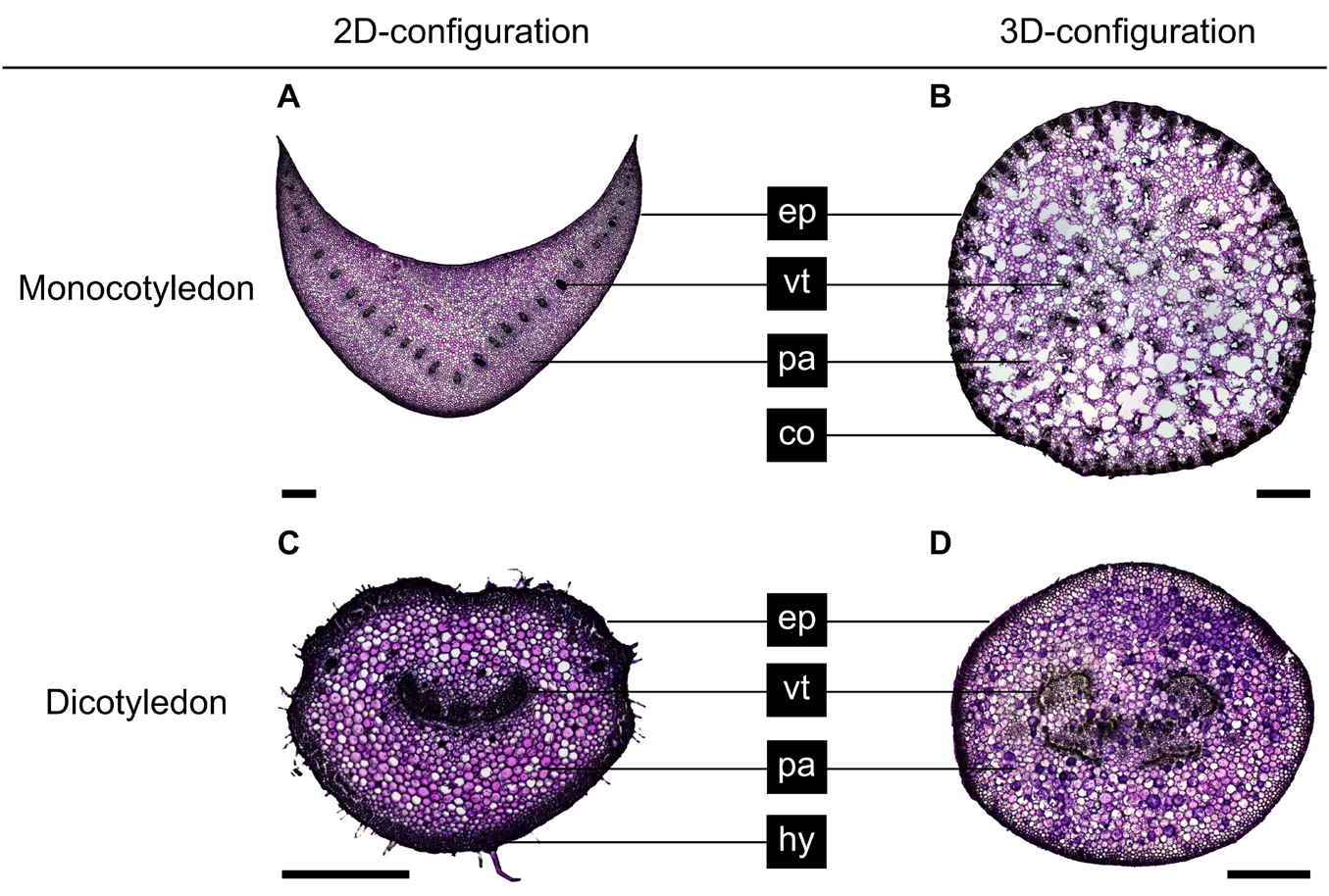
Figure 4. Basal cross-sections of (A) Hosta × tardiana ‘El Niño’, (B) Caladium bicolor, (C) Hemigraphis alternata, and (D) Pilea peperomioides stained with toluidine blue O. Epidermis (ep), vascular tissue (vt), parenchyma (pa), collenchyma (co), and hypodermis (hy) are shown. Scale bars are 1 mm.
Size
The size variables represented by the axial (I) and polar (J) second moment of area and torsion constant (K) of the monocotyledonous petioles were significantly higher than those of the dicotyledonous petioles. Thus, in terms of the size-dependent variables I, J, and K, the petioles of the monocotyledons were more resistant to deformations by bending and torsional loads. Within the dicotyledons, all size variables of P. peperomioides were significantly higher than those of H. alternata. Within the monocotyledons, C. bicolor exhibited significantly higher values for I and K, whereas H. tardiana had a significantly higher J.
Shape
The circular geometry of the petioles of C. bicolor and P. peperomioides was confirmed numerically by their respective aspect ratios of AR ≈ 1.0 and their ratios of the second moments of area of I/J ≈ 0.5. In contrast, we found AR > 1.0 and I/J < 0.5 for the elliptical geometry of H. alternata and the U-profile of H. tardiana. The I/K values of the circular and elliptical geometries ranged between 0.58 and 0.69 and differed significantly from the U-profile of H. tardiana with 1.08 (Figure 5D). Thus, H. tardiana has the comparably smallest K in relation to its I. The weight ratio WR of the lamina and petiole was balanced in H. tardiana, whereas the lamina of C. bicolor only weighed approx. 2/3 the weight of the petiole. In comparison, the lamina of dicotyledons H. alternata and P. peperomioides weighed several times the weight of the petiole, showing that the petioles of the dicotyledons carried, in relation to their own weight, significantly more weight than those of the monocotyledons. The petioles of C. bicolor were linearly tapered (α ≈ 1) and differed significantly from the other investigated species. The petioles of the other species were more hyperbolically tapered (α > 1), i.e., their cross-sections tapered faster in the apical direction than those of C. bicolor.
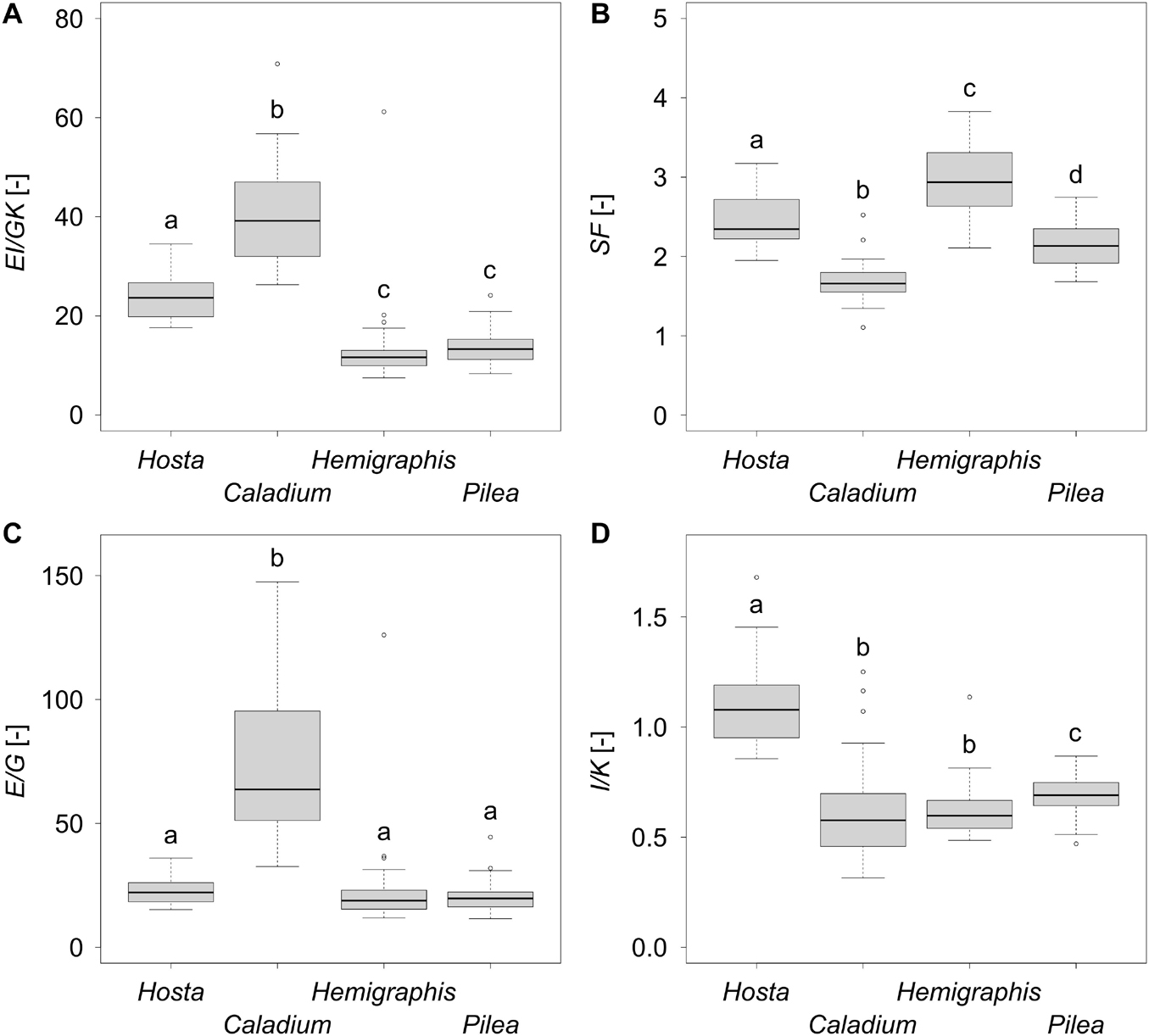
Figure 5. Boxplots of (A) the twist-to-bend ratio EI/GK, (B) the safety factor SF, (C) the ratio of the elastic to the torsional modulus E/G, and (D) the ratio of the axial second moment of area to the torsion constant I/K of 25 leaves each of the species Hosta x tardiana ‘El Niño’, Caladium bicolor, Hemigraphis alternata, and Pilea peperomioides. Significant differences (p-value < 0.05) are indicated by lower case letters.
Biomechanics
The bending elastic moduli E of all species were between 100 and 200 MPa. In particular, E of P. peperomioides was significantly smaller than those of the other species. Furthermore, E of H. tardiana was significantly smaller than that of C. bicolor. Therefore, with respect to the material property E, C. bicolor and H. alternata were more resistant against deformation by bending loads. Although the torsional moduli G were within a single-digit megapascal range, all torsional moduli G differed significantly with the exception of H. tardiana and P. peperomioides. Caladium bicolor had the lowest G, i.e., it exhibited the lowest material-based resistance to torsion. In contrast, H. alternata had the highest G and thus the highest material-based resistance to torsion. The median E/G for all species was about 20, except for C. bicolor, which had a significantly higher E/G of 63 (Figure 5C). The flexural and torsional rigidities EI and GK of the monocotyledonous petioles were significantly higher than those of the dicotyledonous petioles, which suggested that the monocotyledonous petioles were structurally better equipped to withstand bending and torsional loads. All twist-to-bend ratios EI/GK were above 10, showing that the petioles of all species studied were much easier to twist than to bend. However, the EI/GK ratio of the monocotyledons were significantly higher than those of the dicotyledons (Figure 5A). Among the studied monocotyledons, C. bicolor had the highest EI/GK ratio. The twist-to-bend ratios of the dicotyledons did not differ significantly. All safety factors showed significant differences with their medians ranging between 1.66 and 2.94 (Figure 5B).
Discussion
As almost all variables studied showed significant differences, the aim of our screening process to select four different types of petioles as models for the two body plans and two configurations was successful. Nevertheless, we found similarities and dissimilarities between them. Generally, the high flexural rigidity of the petioles guarantees an optimal alignment of the lamina to sun light. This applies to loads arising from their own weight and to additional loads such as wind, rain, and snow. Streamlining in wind, however, is achieved both by the bending and twisting of the petioles and by the folding of the lamina (Vogel, 1989).
High Twist-to-Bend Ratios
In general, high flexural rigidity (EI) combined with low torsional rigidity (GK) results in high twist-to-bend ratios (EI/GK). With a viewpoint on geometry, high twist-to-bend ratios thus result from high values of the axial second moment of area I compared with the torsion constant K (I/K > 1.0); in our study, this is true for the U-profile of the petiole of H. tardiana. With a focus on material properties, high twist-to-bend ratios can be the result of a high elastic modulus E and a relatively low torsional modulus G (E/G > > 1.0); this holds true for most plant organs (Niklas, 1999).
Since the polar second moment of area J is the sum of the perpendicular axial second moments of area I in x- and y-direction, the ratio of Ix/J and Iy/J can never exceed 1.0. For a perfect circular cross-section, I/J = 0.5. In this case, K is equal to J because circular cross-sections do not warp under torsional loading (Young et al., 2002; Etnier, 2003; Gere, 2004). However, all other geometries undergo warping under torsional loading and should be characterized by the torsion constant K, which is smaller than J and, thus, markedly influences GK and EI/GK. For example, K of the U-profile of the petiole of H. tardiana is 3.77 times smaller than the corresponding J. Furthermore, K of the ellipse of the petiole of H. alternata is 1.63 times smaller than J. Even for the almost circular cross-sections of C. bicolor and P. peperomioides, K is 1.05 and 1.37 smaller than J because biological samples are never perfectly circular. Since the literature values mostly refer to J and not to K, we will use EI/GJ for the comparative discussion on the twist-to-bend ratio. However, these twist-to-bend ratios from the literature might be underestimated, because EI/GJ < EI/GK.
In the literature, exceptionally high twist-to-bend ratios (EI/GJ) are described for the U-profiled petioles of Musa textilis (Figure 6) and the triangular flower stalks of Carex pendula. Leaves of Musa textilis have long petioles with a pronounced taper and two large lamina halves. The petioles are U-profiled, similar to those of H. tardiana, and reveal an inner and outer shell with fiber-reinforced radial strands. This structure makes the petiole 40- to 100-fold stiffer in bending than in torsion (Ennos et al., 2000). In other words, the petiole is stiff enough to prevent the leaf from bending downwards and flexible enough to support streamlining by torsion. Peak values of up to 400 have been found in the triangular cross-sections of the flower stalk of Carex pendula (Speck et al., 2020). The high twist-to-bend ratios derive from high ratios of the bending elastic modulus and torsional modulus (E/G) with median values of 438. Flower stalks and leaf petioles, as all plant axes, consist of several tissues, and not only the presence of these tissues but also the tissue arrangement and distribution in the plant axes is important for the mechanical properties. This holds true especially for strengthening tissues like vascular bundles, collenchyma, and sclerenchyma. In the case of the C. pendula flower stalks the peripheral arrangement of the individual sclerenchyma strands, in combination with the high elastic modulus of sclerenchyma, is predominantly responsible for the high flexural rigidity of the flower stalks (Niklas, 1999; Wolff-Vorbeck et al., 2021). On the other hand, according to Wolff-Vorbeck et al. (2021), the reinforcement by not connected individual sclerenchyma strands only moderately increases the torsional rigidity of the entire stalk. While the bending stiffness remains almost constant with an increasing number of peripheral sclerenchyma strands, the torsional rigidity shows a minimum and the twist-to-bend ratio a maximum at 49 sclerenchyma strands. The results found for flower stalks of C. pendula can be transferred to the petioles of C. bicolor showing a similar arrangement of individual strands of strengthening tissues in the periphery. This applies even though the petioles of C. bicolor have a circular cross-section and possess collenchyma fibers instead of sclerenchyma fibers.

Figure 6. Schematic drawings of the cross-sectional geometries and strengthening tissues (black) of various petioles and their corresponding twist-to-bend ratios. The cross-sectional schematics are colored in blue for dicotyledons and in green for monocotyledons.
In this context, the different biomechanical properties of the strengthening tissues play a major role. Vascular bundles typically exhibit elastic moduli ranging from 30 to 840 MPa. Sclerenchyma, a dead and thick-walled strengthening tissue, is almost as stiff as wood under bending and twisting (Niklas, 1999). Sclerenchyma fibers, as found in C. pendula, have elastic moduli between 22,600 and 45,000 MPa (Niklas, 1992; Speck and Schmitt, 1992; Speck et al., 2018; Bold et al., 2020; Speck and Speck, 2021). In contrast, collenchyma, as present in C. bicolor petioles, is a living, hydrostatic and pronounced viscoelastic tissue, which is thus capable of large extensions, but at the same time restores itself after the removal of the external forces (Niklas, 1999). Therefore, the elastic modulus of collenchyma is markedly lower and ranges between 1,000 and 2,600 MPa (Ambronn, 1881; Niklas, 1992; Speck and Schmitt, 1992; Speck and Speck, 2021). Both sclerenchyma and collenchyma are important strengthening tissues in all types of plant axes. They resist bending and torsional loads through high stiffness and/or absorb these loads through their viscoelasticity.
Tapering Mode
The petiole can be considered as a horizontal cantilever or vertical pole that is fixed at one end and in which the load of the lamina is applied to the free end. Thus, the larger the tapering mode, the more weight can be saved in the apical region, whereby its own weight and the acting leverage (in the horizontal orientation) are minimized (Figure 2). In this study, the applied weight of the lamina differs markedly and ranges from 0.6 to 7.5 times the petiole weight. Interestingly, the petiole of H. alternata has the smallest values for flexural rigidity but carries the highest top load in relation to its weight. In this context, Silk et al. (1982) have pointed out that tapered axes apically have a lower flexural rigidity, which leads to a bending at the tip and a reduction of the moment arm produced by the top load (e.g., lamina, flowers, fruits). The calculation of the tapering mode α is also essential for another reason. For calculations of mechanical properties, the tapering mode is of particular importance because its omission can lead to their considerably overestimation. For the petioles of Caladium bicolor “Candyland” Caliaro et al. (2013) have determined a tapering mode of 0.82. By considering this tapering mode, the flexural rigidity decreases to 59% of the value without the taper. Similarly, the flower stalks of C. pendula have a tapering mode of 1.37, which reduces the flexural rigidity to 88% of the value without the taper (Speck et al., 2020).
Leaves With 2D-Configuration
Leaves with a 2D-configuration, such as those of H. tardiana and H. alternata, are mostly horizontally oriented. In this context, elliptical cross-sections with a groove, as in H. alternata, Phaseolus vulgaris and Liquidambar styraciflua, or U-profiles, as in H. tardiana and Musa textilis, are advantageous as they are resistant to downward bending. In addition, these cross-sections allow for high torsional flexibility, making them well suited for handling wind loads through streamlining (Figure 6; Vogel, 1992; Ennos et al., 2000; Wolff-Vorbeck et al., 2019). A contrary influence is the closed ring of peripheral strengthening tissue, i.e., the hypodermis of H. alternata, which increases flexural and torsional rigidities (Figure 4; Niklas, 1999).
Leaves With 3D-Configuration
The petioles of leaves with a 3D-configuration grow vertically but are sometimes slightly inclined not only as a result of growth processes, but also because of the eccentric connection of the petiole to the lamina and the associated slightly asymmetric weight distribution. Peltate leaves often possess petioles with an almost circular cross-section, as found in C. bicolor and P. peperomioides, which causes no preferred or disadvantaged bending force direction attributable to the apical load caused by the lamina (Vogel, 1992; Sacher et al., 2019). The petioles of C. bicolor show a low I/K ratio but their E/G ratio is more than three times higher than that of the other petioles tested resulting in high twist-to-bend ratios (Figure 6). The high E/G ratio of C. bicolor petioles is due to the fact that they have in median the highest E and lowest G of the species studied. The high E can be explained by the already described peripherally arranged strengthening tissue in the form of collenchyma fibers. The low torsional rigidity can be attributed to the arrangement of the strengthening tissues (vascular and collenchyma bundles) in separate individual not connected strands. This tissue arrangement is quite flexible in torsion, as mentioned earlier, compared to closed rings of strengthening tissues as found in H. alternata (Niklas, 1999; Ennos et al., 2000; Wolff-Vorbeck et al., 2021).
Overall, the material properties E and G of all the species studied are of a similar magnitude and have typical values for organs of non-lignified herbaceous plants (Speck and Speck, 2021). With regard to the monocotyledons studied, the high values of I, J, and K result from their broader petioles and lead to significant differences in flexural and torsional rigidities. The high flexural rigidities of these monocotyledons, in turn, translate into their significantly higher twist-to-bend ratios (Figure 6).
Safety Factors
The safety factors ranging between 1.66 and 2.94 indicate that each petiole can carry about twice to triple the static load of the leaf, leaving enough margin for additional loads such as wind or rain. This agrees well with the reported safety factor of biological structures, such as the flower stalk of the monocotyledonous Allium sativum with a safety factor of 1.85 ± 0.29 (Niklas, 1990) or the stems of the dicotyledonous Populus tremuloides with an average safety factor of 2.3 (King and Loucks, 1978). In contrast, large old record-sized trees, when only their own weight is considered, are mechanically “overbuilt” and have a safety factor of over 4 (McMahon, 1973; King and Loucks, 1978; Niklas, 1992). In herbaceous plants, however, the safety factor depends on the turgescence of the tissues. Fully turgescent peduncles of the dicotyledonous Gerbera jamesonii ‘Nuance’ have a safety factor of 1.42. This is different in wilted peduncles, which have a safety factor of 0.95 and cause pronounced drooping of their flower heads (Lehmann et al., 2019).
Conclusion
With respect to our scientific question of “How do cross-sectional geometry, sizes and shapes of petioles influence their twist-to-bend ratio and safety factor?” we can make some general statements:
• High twist-to-bend ratios allow the petiole to be stiff enough to withstand bending loads caused by the self-weight of the leaf and to be flexible enough to twist away from damaging influences such as wind loads.
• Strengthening tissue in the periphery (e.g., fibers, hypodermis) increases flexural rigidity.
• Closed peripheral rings of strengthening tissue (e.g., hypodermis) markedly increase torsional rigidity. Individual strands of strengthening tissue (e.g., fiber strands) do not markedly increase torsional rigidity. Adaxial grooves (e.g., U-profile) decrease torsional rigidity.
• With the exception of perfect circular cross-sections, the polar second moment of area J is considerably larger than the torsion constant K, the latter value having been calculated by taking into account warping under torsional loading.
• Since K < J, it follows that EI/GJ < EI/GK, which leads to an underestimation of the “real twist-to-bend ratios” of structures with cross-sections exhibiting warping, if J is used for calculating the twist-to-bend ratio.
• High twist-to-bend ratios can be geometry-related if I/K > 1.0, which is rare, and/or material-related if E/G > > 1.0, which holds true for most plant organs.
• The safety factor, here defined as the ratio of maximal length to real length, describes the extent to which the petiole can support more than its own weight.
• Equations to calculate the safety factor are now available for horizontally and vertically oriented leaves.
• The safety factor of herbaceous plants depends on their turgor.
In addition to the above-mentioned general statement, our comparative morphological, anatomical and biomechanical investigations of four petiole types have revealed further dissimilarities and similarities:
• The petioles differ in most of the variables that we have measured and calculated, namely geometry, shape, size, and mechanics.
• The twist-to-bend ratios of the petioles of the monocotyledons H. tardiana and C. bicolor are significantly higher than those of the dicotyledons H. alternata and P. peperomioides.
• Dependent on the cross-sectional geometry of the petioles, the torsion constant K is smaller than J as follows: 3.77 times smaller for the U-profile of H. tardiana, 1.63 times smaller for the ellipse of H. alternata, 1.37 times smaller for the circle of P. peperomioides and 1.05 times smaller for the circle of C. bicolor.
• The U-profiles of H. tardiana is the only one with an I/K > 1.0.
• The E/G of C. bicolor is three times as high as that of the other petioles.
• The safety factors strongly indicate that each of the petioles studied can support about double to triple the leaf’s own weight, with sufficient tolerance for additional loads such as wind.
In conclusion, our results show that high twist-to-bend ratios, i.e., high flexural rigidity and low torsional rigidity, can be achieved by geometrical-based (U-profile) or by material-based (high E/G ratio) conditions. On the other hand, some plant axes show low twist-to-bend ratios, i.e., low flexural rigidity and high torsional rigidity, which can even be smaller than 1 in special cases. For example, cross-sections with a peripheral closed ring of strengthening tissue show high torsional rigidity. These results for plant petioles and flower stalks can be transferred to other rod-shaped axes of plants and animals with different cross-sectional geometry. Furthermore, our findings may serve as inspiration for technical applications using rod-shaped axes. In the framework of a biomimetic approach, axes with high or low twist-to-bend ratios can be created by transferring our findings regarding the importance of cross-sectional geometry and arrangement of strengthening elements or ratios of material properties. Based on the results of the present study, the question arises what influence the cross-sectional geometry and/or arrangement of strengthening tissues have on the flexural and torsional rigidity and thus on the twist-to-bend ratio in general. A further systematic study on this topic using a modeling approach is in progress and will provide further information about the mechanical performance of plant axes and can also be a starting point for engineers to develop bioinspired solutions.
Moreover, our calculations revealed safety factors for herbaceous fully turgescent plants between 2 and 3. Interestingly, a safety factor between 1.2 and 3.0 is used in engineering, depending on the materials used and the particular application. In the case of a wilting plant, the safety factor decreases and can even fall below 1, meaning that the structure will eventually fail. However, the turgor-dependent change of safety factors in herbaceous plants may be an inspiration for technical solutions, where a variation of mechanical properties with a concomitant change/adaptation of the safety factor depending on the phase of use might be beneficial.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
ML, CM, TS, and OS designed the study, performed the biomechanical analyses, and wrote the final draft of the manuscript. MK and ML collected the data and performed the statistical analyses. ML and OS wrote the first draft of the manuscript. All authors contributed significantly to the intellectual content of the final draft, revised the article, approved the final version of the manuscript, and agree to be held responsible for the content therein.
Funding
This work was funded by the State Ministry of Baden-Wuerttemberg for Sciences, Research and Arts in the framework of the collaborative project “Bio-inspirierte elastische Materialsysteme und Verbundkomponenten für nachhaltiges Bauen im 21ten Jahrhundert” (BioElast) within the “Zukunftsoffensive IV Innovation und Exzellenz—Aufbau und Stärkung der Forschungsinfrastruktur im Bereich der Mikro- und Nanotechnologie sowie der neuen Materialien”, and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC-2193/1—390951807. The article processing charge was partly funded by the University of Freiburg in the funding program Open Access Publishing.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank the team of the Botanic Garden Freiburg for their care of the test plants. Our thanks are also extended to R. Theresa Jones for improving the English.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2021.765605/full#supplementary-material
References
Ambronn, H. (1881). Über die Entwickelungsgeschichte und die mechanischen Eigenschaften des Collenchyms. Jahrbuch Wissenschaftliche Botanik 12, 473–541.
Bold, G., Langer, M., Börnert, L., and Speck, T. (2020). The protective role of bark and bark fibers of the giant sequoia (Sequoiadendron giganteum) during high-energy impacts. Int. J. Mol. Sci. 21:3355. doi: 10.3390/ijms21093355
Caliaro, M., Schmich, F., Speck, T., and Speck, O. (2013). Effect of drought stress on bending stiffness in petioles of Caladium bicolor (Araceae). Am. J. Bot. 100, 2141–2148. doi: 10.3732/ajb.1300158
Doube, M., Kłosowski, M. M., Arganda-Carreras, I., Cordelières, F. P., Dougherty, R. P., Jackson, J. S., et al. (2010). BoneJ: free and extensible bone image analysis in ImageJ. Bone 47, 1076–1079. doi: 10.1016/j.bone.2010.08.023
Drost, H.-G., Janitza, P., Grosse, I., and Quint, M. (2017). Cross-kingdom comparison of the developmental hourglass. Curr. Opin. Genet. Dev. 45, 69–75. doi: 10.1016/j.gde.2017.03.003
Ennos, A. R., Spatz, H.-C., and Speck, T. (2000). The functional morphology of the petioles of the banana, Musa textilis. J. Exp. Bot. 51, 2085–2093. doi: 10.1093/jexbot/51.353.2085
Etnier, S. A. (2003). Twisting and bending of biological beams: distribution of biological beams in a stiffness mechanospace. Biol. Bull. 205, 36–46. doi: 10.2307/1543443
Gallenmüller, F., Müller, U., Rowe, N. P., and Speck, T. (2001). The growth form of Croton pullei (Euphorbiaceae) - functional morphology and biomechanics of a neotropical liana. Plant Biol. 3, 50–61. doi: 10.1055/s-2001-11750
Greenhill, A. G. (1881). Determination of the greatest height consistent with stability that a vertical pole or mast can be made, and of the greatest height to which a tree of given proportions can grow. Proc. Camb. Philos. Soc. 4, 65–73.
King, D., and Loucks, O. L. (1978). The theory of tree bole and branch form. Radiat. Environ. Biophys. 15, 141–165. doi: 10.1007/BF01323263
Langer, M., Speck, T., and Speck, O. (2021). Petiole-lamina transition zone: a functionally crucial but often overlooked leaf trait. Plants 10:774. doi: 10.3390/plants10040774
Lehmann, L.-S., Kampowski, T., Caliaro, M., Speck, T., and Speck, O. (2019). Drooping of Gerbera flower heads: mechanical and structural studies of a well-known phenomenon. Biol. Lett. 15:20190254. doi: 10.1098/rsbl.2019.0254
McMahon, T. (1973). Size and shape in biology: elastic criteria impose limits on biological proportions, and consequently on metabolic rates. Science 179, 1201–1204. doi: 10.1126/science.179.4079.1201
Niinemets, Ü, and Fleck, S. (2002). Petiole mechanics, leaf inclination, morphology, and investment in support in relation to light availability in the canopy of Liriodendron tulipifera. Oecologia 132, 21–33. doi: 10.1007/s00442-002-0902-z
Niklas, K. J. (1990). Determinate growth of Allium sativum peduncles: evidence of determinate growth as a design factor for biomechanical safety. Am. J. Bot. 77, 762–771. doi: 10.2307/2444368
Niklas, K. J. (1992). Plant Biomechanics: An Engineering Approach to Plant Form and Function. Chicago, IL: University of Chicago Press.
Niklas, K. J. (1996). Differences between Acer saccharum leaves from open and wind-protected sites. Ann. Bot. 78, 61–66. doi: 10.1006/anbo.1996.0096
Niklas, K. J. (1999). A mechanical perspective on foliage leaf form and function. New Phytol. 143, 19–31. doi: 10.1046/j.1469-8137.1999.00441.x
Pasini, D., and Mirjalili, V. (2006). “The optimized shape of a leaf petiole,” in Design and Nature III: Comparing Design in Nature with Science and Engineering, ed. C. A. Brebbia (Southampton: WIT Press), 35–45.
R Core Team (2021). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Sacher, M., Lautenschläger, T., Kempe, A., and Neinhuis, C. (2019). Umbrella leaves - biomechanics of transition zone from lamina to petiole of peltate leaves. Bioinspir. Biomim. 14:46011. doi: 10.1088/1748-3190/ab2411
Sakai, W. S. (1973). Simple method for differential staining of paraffin embedded plant material using toluidine blue O. Stain Technol. 48, 247–249. doi: 10.3109/10520297309116632
Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. doi: 10.1038/nmeth.2019
Silk, W. K., Wang, L. L., and Cleland, R. E. (1982). Mechanical properties of the rice panicle. Plant Physiol. 70, 460–464. doi: 10.1104/pp.70.2.460
Speck, O., Schlechtendahl, M., Borm, F., Kampowski, T., and Speck, T. (2018). Humidity-dependent wound sealing in succulent leaves of Delosperma cooperi - an adaptation to seasonal drought stress. Beilstein J. Nanotechnol. 9, 175–186. doi: 10.3762/bjnano.9.20
Speck, O., and Speck, T. (2021). Functional morphology of plants - a key to biomimetic applications. New Phytol. 231, 950–956. doi: 10.1111/nph.17396
Speck, O., Steinhart, F., and Speck, T. (2020). Peak values of twist-to-bend ratio in triangular flower stalks of Carex pendula: a study on biomechanics and functional morphology. Am. J. Bot. 107, 1588–1596. doi: 10.1002/ajb2.1558
Speck, T. (1994). A biomechanical method to distinguish between self-supporting and non self-supporting fossil plants. Rev. Palaeobot. Palynol. 81, 65–82. doi: 10.1016/0034-6667(94)90127-9
Speck, T., and Schmitt, M. (1992). “Mechanische Werte,” in Lexikon der Biologie - Biologie im Überblick, ed. M. Schmitt (Freiburg: Herder), 244–247.
Vogel, S. (1989). Drag and reconfiguration of broad leaves in high winds. J. Exp. Bot. 40, 941–948. doi: 10.1093/jxb/40.8.941
Vogel, S. (1992). Twist-to-bend ratios and cross-sectional shapes of petioles and stems. J. Exp. Bot. 43, 1527–1532. doi: 10.1093/jxb/43.11.1527
Vogel, S. (1995). Twist-to-bend ratios of woody structures. J. Exp. Bot. 46, 981–985. doi: 10.1093/jxb/46.8.981
Vogel, S. (2007). Living in a physical world XI. To twist or bend when stressed. J. Biosci. 32, 643–655. doi: 10.1007/s12038-007-0064-6
Wainwright, S. A., Biggs, W. D., Currey, J. D., and Gosline, J. M. (1976). Mechanical Design in Organisms. Princeton, NJ: Princeton University Press.
Wolff-Vorbeck, S., Langer, M., Speck, O., Speck, T., and Dondl, P. (2019). Twist-to-bend ratio: an important selective factor for many rod-shaped biological structures. Sci. Rep. 9:17182. doi: 10.1038/s41598-019-52878-z
Wolff-Vorbeck, S., Speck, O., Speck, T., and Dondl, P. (2021). Influence of structural reinforcements on the twist-to-bend ratio of plant axes: a study of Carex pendula. Sci. Rep. 11:21232. doi: 10.1038/s41598-021-00569-z
Keywords: twist-to-bend ratio, safety factor, petiole, biomechanics, body plan, geometry, size, shape
Citation: Langer M, Kelbel MC, Speck T, Müller C and Speck O (2021) Twist-to-Bend Ratios and Safety Factors of Petioles Having Various Geometries, Sizes and Shapes. Front. Plant Sci. 12:765605. doi: 10.3389/fpls.2021.765605
Received: 27 August 2021; Accepted: 20 October 2021;
Published: 11 November 2021.
Edited by:
Sanna Sevanto, Los Alamos National Laboratory (DOE), United StatesReviewed by:
Monica Carvalho, Smithsonian Tropical Research Institute, PanamaYihua Zhou, University of Chinese Academy of Sciences, China
Copyright © 2021 Langer, Kelbel, Speck, Müller and Speck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Max Langer, bWF4LmxhbmdlckBiaW9sb2dpZS51bmktZnJlaWJ1cmcuZGU=
 Max Langer
Max Langer Mark C. Kelbel
Mark C. Kelbel Thomas Speck
Thomas Speck Claas Müller
Claas Müller Olga Speck
Olga Speck